一、
智能反射平面（intelligent reflecting surfaces）是一种被动反射表面，其具有的特性是可控制反射信号的相位。
明确IRS是可控制反射信号的相位，所以以单个智能反射单元为例，该单元可调信号的参数可表示为
，由于智能反射单元是被动反射的，所以准确来说
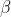是无法控制的，在控制信号大小方面，智能反射单元是鸡肋，它顶多充当一面反射墙，
，也就是说信号经过反射之后可能100%反射出去，也可能有损耗，最差的情况是一点都没反射出去。所以一般考虑最美好的状况就是，如此智能反射单元的系数就是
。如此智能反射单元的系数就是
明确信号的性质，信号可以用向量表示，正是因为信号有大小和方向，大小即为信号的强度大小，方向即为信号的相位，也就是延迟。这也就是为什么只能反射面可应用于物理层的原因。
step1:信号的生成，生成可以被计算机识别的01序列。
%场景是一个发射机，一个接收机和智能反射表面。data = round(rand(1, N)); %产生N个随机二进制原始数据0,1step2:信号调制
s=pskmod(data,4); %调用matlab自带的psk调制函数step3:设置信道状态信息CSI
hAI = (randn(unit_n,1)+1i*randn(unit_n,1))/sqrt(2); %发射机和智能反射面之间的信道衰落系数hIB = (randn(unit_n,1)+1i*randn(unit_n,1))/sqrt(2); %智能反射面和接收机之间的信道衰落系数step4:设置智能反射单元反射系数
IRS_Phase = exp(1i.*theta_IRS); %IRS的相位控制step5:设置接收端的噪声
sigma_noise = sqrt(1/2); n = (sigma_noise).*(randn(1,length(s))+1i*randn(1,length(s))); %接收端的噪声模拟step6:接收机收到感知信号
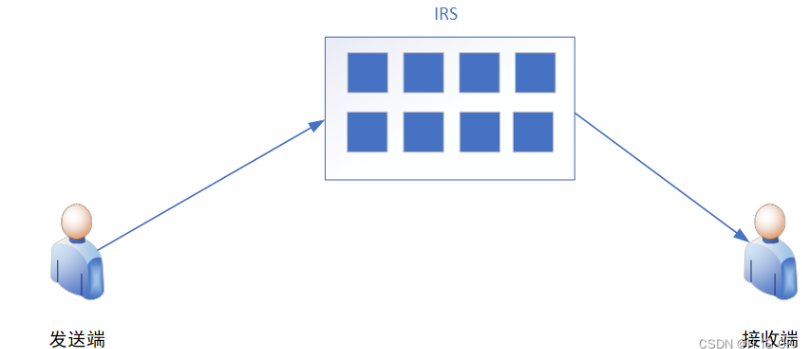
rB = sum(hAI.*IRS_Phase.*hIB)*s + n; %接收端接收经过衰落的已调信号s二、IRS-aided single-user MISO system
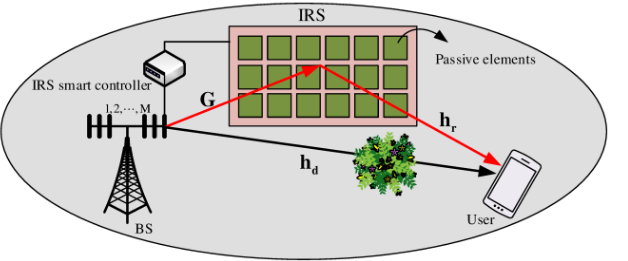
我们考虑现在最热的毫米波信道， 即具有稀疏性， 径数有限。 **另外需要指出的是， 由于IRS是一个平面，因此其天线响应向量（array response vector），应当按照 UPA (uniform planar array) 来算， 而不能按ULA (uniform linear array)。 因此， 其响应可以写为：
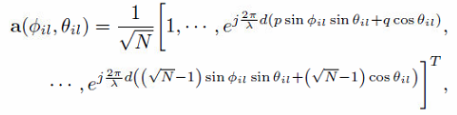
其中， ϕ 和 θ 分别代表了信号入射的方位角 (azimuth angle) 和 仰角 (elevation angle)。 N 代表的是天线总数（智能反射面反射因子数）。 λ 是波长，d 是天线间隔， 一般都设置有d = 0.5 λ
同样的，现在主流的基站的发送天线一般也以UPA形式为主。 因此， BS-IRS信道实际上就是两个UPA之间的MIMO信道仿真。 首先先写一个函数， 来实现单侧UPA的天线响应向量的仿真：
function y = array_response(phi,theta, N)for m= 0:sqrt(N)-1 for n= 0:sqrt(N)-1 y(m*(sqrt(N))+n+1) = exp( 1i* pi* ( m*sin(phi)*sin(theta) + n*cos(theta) ) ); endendy = y.'/sqrt(N);end这里假设了UPA是正方形UPA，即横向和纵向的阵子数相等。 如果想考虑长方形UPA的话可以自行修改， 但如果只是想简单地仿真一个智能反射面信道的话完全可以用上述代码实现
有了这个函数， 就能很快地仿真BS-IRS信道了：
% Nt代表发送天线数， Nr代表接收天线数 L代表路径总数 （1条LOS直射径+(L-1)条NLOS径）function H = generate_channel(Nt, Nr, L) AoD = pi*rand(L, 2) - pi/2; %-2/pi~2/pi 发送的天线角和仰角AOA = pi*rand(L, 2) - pi/2; %-2/pi~2/pi 接受的天线角和仰角% α代表的是信道的衰落系数， 为了区别LOS径和NLOS径，我们默认第一径是LOS径，给了归一化的能量为1% 而NLOS径的能量则是高斯变量， 并且为了体现出与LOS径的能量差， 给了一个衰减系数。alpha(1) = 1; % gain of the LoS alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);H = zeros(Nr, Nt);for l=1:1:L ar = array_response(AOA(L,1),AOA(L,2), Nr); at = array_response(AOD(L,1),AOD(L,2), Nt); H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';endNt 代表发送天线数， Nr代表接收天线数， L代表路径总数 （1条LOS直射径+(L-1)条NLOS径）。
每条径需要包含四个变量： 发送的方位角和仰角； 接收的方位角和仰角。 我们生成AOD， 代表发送的方位角和仰角。
AOD = pi*rand(L, 2) - pi/2; %发送天线的方向角和仰角%相当于生成了 L × 2 个 − 0.5 π -0.5π的角度，其中每条路径各有发送方位角和仰角一个这里相当于生成了 L × 2 个 − 0.5 π -0.5π的角度，其中每条路径各有发送方位角和仰角一个。 AOA同理。
这里需要指出， 实际中方位角和仰角的变化范围应该不同，仰角的变化范围会偏小， 因此更合理的仿真应该进一步限制其生成范围。 但就像上面所说，如果只是为了随机生成智能反射面信道用于仿真，不用纠结的那么细。
α代表的是信道的衰落系数， 为了区别LOS径和NLOS径，我们默认第一径是LOS径，给了归一化的能量为1。 而NLOS径的能量则是高斯变量， 并且为了体现出与LOS径的能量差， 给了一个衰减系数。
截了下MIMO的H信道公式。 和我们的模型有一点点区别， 但是每一径的生成是一样的，就是根据发送角和到达角分别生成ar和at然后相乘并乘上衰落因子。
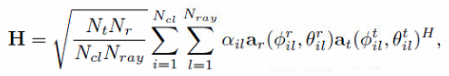
alpha(1) = 1; % gain of the LoS alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);H = zeros(Nr, Nt);for l=1:1:L ar = array_response(AOA(L,1),AOA(L,2), Nr); at = array_response(AOD(L,1),AOD(L,2), Nt); H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';end关于BS-UE的信道， 有几种不同的建模：
直接假设BS-UE间被阻隔， 即不存在这个信道。 即直接链路被阻隔， 即不存在LOS径， 但是有NLOS径。 那么就可以用上面的代码去仿真，只需要把LOS径去掉就行了。
假设为瑞利衰落信道。 这个是最容易仿真的， 也有许多论文采用这个建模。 瑞利的仿真代码非常容易， 网上也有很多，不再赘述了。
三、PARAFAC-Based Channel Estimation for Intelligent Reflective Surface Assisted MIMO System
PARAFAC-Based Channel Estimation for Intelligent Reflective Surface Assisted MIMO System Sim Note_小何的芯像石头的博客-CSDN博客PARAFAC-Based Channel Estimation for Intelligent Reflective Surface Assisted MIMO System Simulation Note文章目录PARAFAC-Based Channel Estimation for Intelligent Reflective Surface Assisted MIMO System Simulation Note论文推导部分张量分解(tensor decomposition)大概思路论文仿真笔记a
智能反射面（IRS）信道建模与仿真_ぁず的博客-CSDN博客_智能反射面irs
混合波束成形| MIMO系统的DFT码本_B417科研笔记的博客-CSDN博客_dft码本
（UPA和ULA区别）
array_response
%采用UPA天线响应。phi为方向角， theta为仰角，N为天线的总数function y = array_response(phi,theta, N) for m= 0:sqrt(N)-1 %sqrt(N)*sqrt(N)=N ，保持行列相等。m控制行数 for n= 0:sqrt(N)-1 % n控制列数 % y(m*(sqrt(N))+n+1)是从y(0)，y(1)....y(N)的响应，然后放到一个1*N的矩阵中 y(m*(sqrt(N))+n+1) = exp( 1i* pi* ( m*sin(phi)*sin(theta) + n*cos(theta) ) ); endendy = y.'/sqrt(N); %将得到的1*N矩阵作转置，在归一化endarray_response这个函数主要计算(阵列)天线增益
由于IRS是一个平面，因此其天线响应向量（array response vector），应当按照 UPA (uniform planar array) 来算。由于已经是方形设计,所以会有两个角度:方向角(azimuth angle),仰角(elevation angle).他们对天线的增益计算如下:
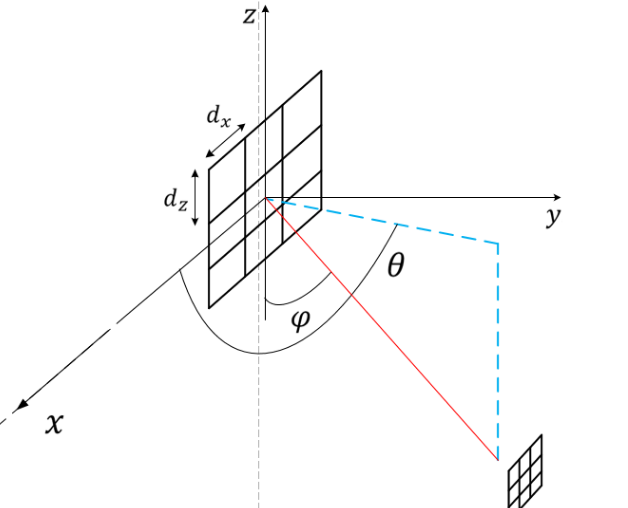
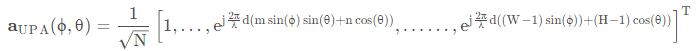
W和H代表了UPA共有W行，H列天线,d为天线间隔.array_response这个函数主要就是计算这个UPA的接收/发送增益,但实际上他发送端不一定是UPA,有可能是ULA(Uniform Linear Array):
对于共N个天线， 天线间隔为半波长(d = λ / 2 )的阵列， 其响应向量可以表示为:
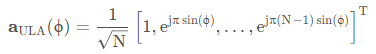
generate_channel /generate_channel_LOS
function H = generate_channel(Nt, Nr, L)AOD = pi*rand(L, 2) - pi/2; %-2/pi~2/piAOA = pi*rand(L, 2) - pi/2; %-2/pi~2/pialpha = (randn(1,L)+1i*randn(1,L))/sqrt(2);H = zeros(Nr, Nt);for l=1:1:L ar = array_response(AOA(l,1),AOA(l,2), Nr); at = array_response(AOD(l,1),AOD(l,2), Nt); H = H + sqrt(Nr * Nt/L)*alpha(l)*ar*at';endfunction [H] = generate_channel_LOS(Nt, Nr, L) %Nt是发送天线数，Nr接受天线数，L路径总数（信道数）%rand(L,2)得到L行，2列在1以内的随机矩阵，pi*rand(L,2)是pi倍L*2的随机数。%AoA 是利用单一天线发射信号，而接收终端内置天线阵列，当信号通过时，会因阵列天线接收的距离不同而产生相位差，进而计算出信号的方向。%AoD 则正好相反，由具备阵列天线的设备来发射信号，传给单一天线终端，接收终端可以通过接收到的信号计算出来波的方向，进而定位。AOD = pi*rand(L, 2) - pi/2; %生成L*2个-2/pi~2/pi的角度。每条路各有发送的方向角和仰角一个，共有L路。ADO为发送的方向角和仰角。AOA = pi*rand(L, 2) - pi/2; % -2/pi~2/pi。AOD到达的方向角和仰角。%randn：产生均值为0，方差σ^2 = 1，标准差σ = 1的正态分布的随机数或矩阵的函数。%Y = randn(n)：返回一个n*n的随机项的矩阵。如果n不是个数量，将返回错误信息。%Y = randn(m,n) 或 Y = randn([m n])：返回一个m*n的随机项矩阵。alpha(1) = (randn(1) + 1j * randn(1)) / sqrt(2); % gain of the LoS，sqrt(2)到达角和仰角只有两参数。alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);H = zeros(Nr, Nt);for l=1:1:L ar = array_response(AOA(l,1),AOA(l,2), Nr); %AOA(l,1)发送的方向角，AOA(l,2)发送仰角，Nr为发射天线的总数 at = array_response(AOD(l,1),AOD(l,2), Nt); %AOD(l,1)到达的方向角，AOD(l,2)到达的仰角，Nt用户天线的总数 H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';endH = H / sqrt(L);对普通的MIMO信道来说,他的每一个子信道服从:
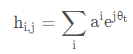
信道增益的模
服从瑞利分布，如果除了大量的散射体还有一个很强的直射路径，则信道增益的模
服从莱斯分布。
而在毫米波信道中,此处的天线增益计算中,不管是ULA还是UPA,信道增益在天线处都服从:
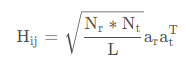
其中
为发送端天线, 为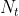
接受端天线,L为路径总数. 为了凸显出LOS径和NLOS的区别,加上一个衰减因子α ,并以LOS径为1, NLOS服从高斯分布
alpha(1) = (randn(1) + 1j * randn(1)) / sqrt(2); % gain of the LoSalpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);所以现在信道增益(单用户/单散射簇)的总体表达式为:
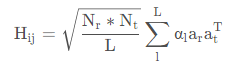
根据array_response中的描述,此时我们需要知道在T/R端的天线角度,此处有一个假设,由于基站到IRS和IRS到用户的距离足够远,导致信号在UPA的接收端的到达角AoA (Angle of Arrival)和发射端的出发角AoD(Angle of Departure)对不同的天线在同一径上是一致的.
所以上式中的信道增益具化为:
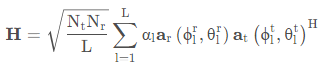
至此就是需要在仿真中用到的仿真公式了.
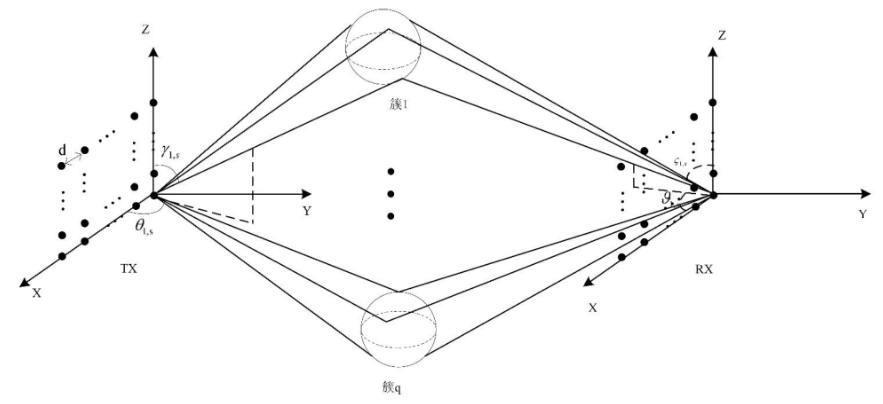
alpha(1) = 1; % gain of the LoS alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);H = zeros(Nr, Nt);for l=1:1:L ar = array_response(AOA(L,1),AOA(L,2), Nr); at = array_response(AOD(L,1),AOD(L,2), Nt); H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';end但对于毫米波信道来说,其可以基于Saleh-Valenzuela模型描述的窄带聚集簇毫米波信道进行建模,即对不同散射簇有:
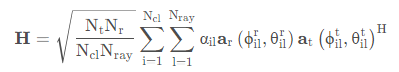
gen_DFTmatrix
“An Optimal Channel Estimation Scheme for Intelligent Reflecting Surfaces based on a Minimum Variance Unbiased Estimator,
四、Compressed Channel Estimation and Joint Beamforming for Intelligent Reflecting Surface-Assisted Millimeter Wave Systems
智能发射面| 信道估计与代码复现： 基于压缩感知_B417科研笔记的博客-CSDN博客_压缩感知信道估计算法代码
智能反射面（IRS）论文复现_样子困的博客-CSDN博客_智能反射面
信道模型与稀疏表示
clear;
N = 16; % 基站天线的个数
Mx = 8; % rows of IRS
My = 8; % columns of IRS
M = Mx * My; % total elements of IRS
NG = 64; % number of codewords of IRS （IRS码字个数）
MG_x = 32;
MG_y = 32;
MG = MG_x * MG_y;
L = 3; % paths of BS-IRS
Lprime = 3; % paths of IRS-UE
T = 1500;
文章先考虑了一个单用户单天线场景。 根据几何建模， 基站-反射面 （BS-IRS)信道可以表示为：
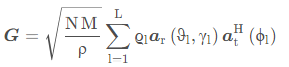
智能反射面为平面， 因此按UPA建模， 而基站为ULA线天线， 因此
也就是说， 反射面端的响应同时与
和 
即仰角和水平角相关。 其中，
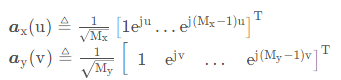
G = 0;
for l = 1 : L % L is paths
ax = 1 / sqrt(Mx) * exp(1j * (0 : Mx-1)' * (2 * rand() - 1)); % (2 * rand() - 1)衰减因子
ay = 1 / sqrt(My) * exp(1j * (0 : My-1)' * (2 * rand() - 1));
ar = kron(ax, ay); % IRS （UPA）的响应
at = 1 / sqrt(N) * exp(1j * (0 : N-1)' * (2 * rand() - 1)); %发射天线（ULA）的响应。
G = G + sqrt(2)/2 * ar * at';
end
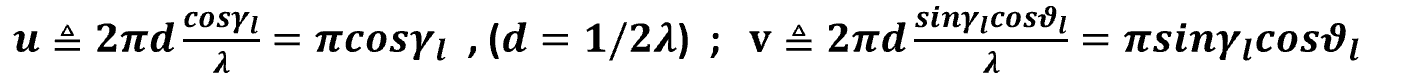
很容易地，对G做SVD，我们有：
也就是经典地信道的压缩感知写法， 其中
, 
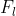可以分别理解为UPA响应和ULA响应的码本。因此，
就是一个只有L个非零元素的稀疏矩阵。第l个非零元素的位置（第i 行, 第j列）分别揭示了第l径对应于哪两个码字(也就是
)以及其增益（也就是
)
FL = 1 / sqrt(N) * exp(1j * (0 : N-1)' * (-1 : 2 / NG : 1 - 2/NG)); %ULA 的码本
Fx = 1 / sqrt(Mx) * exp(1j * (0 : Mx-1)' * (-1 : 2 / MG_x : 1 - 2/MG_x));
Fy = 1 / sqrt(My) * exp(1j * (0 : My-1)' * (-1 : 2 / MG_y : 1 - 2/MG_y));
Fp = kron(Fx, Fy); % UPA 的码本
同理， IRS-UE的信道可以压缩写为：
其中α 是一个只有L ′ 个非零值的稀疏向量。
hr = 0;
for l = 1 : Lprime % Lprime is paths of IRS-UE
ax = 1 / sqrt(Mx) * exp(1j * (0 : Mx-1)' * (2 * rand() - 1));
ay = 1 / sqrt(My) * exp(1j * (0 : My-1)' * (2 * rand() - 1));
ar = kron(ax, ay); % IRS是UPA响应
hr = hr + sqrt(M / Lprime) * sqrt(2)/2 * ar;
end
信道估计
在IRS的信道估计中， 其实就是估计级联信道， 即：
H = diag(hr') * G;
基于上述的压缩表示， 我们进一步推导：
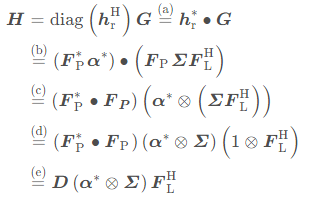
[注]
=
先取复共轭(conj)在对角化。
D=
即
先对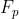
取复共轭（conj）在对
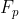对角化。
Fp = kron(Fx, Fy);
f = conj(Fp(:, 1)); %按行的方式对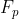
中所有元素取复共轭
Du = diag(f) * Fp;
其中(b)步就是把一开始信道建模时的压缩表示代入，（c）就是利用了 transposed Khatri-Rao product 的性质：
(d)继续使用了克罗内克积的性质，
现在，我们可以将式子进一步简化：
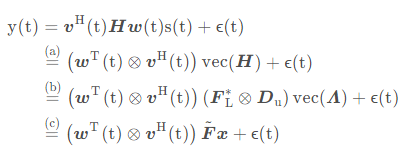
其中，
最后
其中，
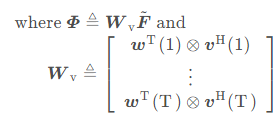
for t = 1 : T
w = 1 / sqrt(N) * exp(1j * (0 : N-1)' * (2 * rand() - 1));
v = 1 / sqrt(N) * exp(1j * (0 : M-1)' * (2 * rand() - 1));
W = [W; kron(w.', v')];
y(t) = v' * H * w + n;
end
phi = W * F_hat;
完整代码：
clc
clear;
close all;
N = 16; %transmit antennas
Mx = 8; % rows of IRS
My = 8; % columns of IRS
M = Mx * My; %total elements of IRS
NG = 64; % number of codewords of IRS
MG_x = 32;
MG_y = 32;
MG = MG_x * MG_y;
L = 3; % paths of BS-IRS
Lprime = 3; % paths of IRS-UE
T = 110;
K=10^1.32; %莱斯因子
FL = 1 / sqrt(N) * exp(pi*1j * (0 : N-1)' * (0 : 1/ NG : 1 - 1/NG));
Fx = 1 / sqrt(Mx) * exp(pi*1j * (0 : Mx-1)' * (0 : 1 / MG_x : 1 - 1/MG_x));
Fy = 1 / sqrt(My) * exp(pi*1j * (0 : My-1)' * (-1/2 : 1 / MG_y : 1/2 - 1/MG_y));
Fp = kron(Fx, Fy);
[m,n]=size(Fp);
D=zeros(m,n*n);
for i=1:m
D(i,:)=kron(conj(Fp(i,:)),Fp(i,:));
end
Du=D(:,1:MG);
v = ones(M, 1);
F_hat = kron(conj(FL), Du);
W =[];
SNR=-10:5:30;%信噪比
count=1;%计数
num=70;%重复次数
NMSE=zeros(num,length(SNR));
NMSE1=zeros(num,length(SNR));
for m=1:num %重复num次
for l = 1 : L
ax = 1 / sqrt(Mx) * exp(pi*1j * (0 : Mx-1)' * (rand()));
ay = 1 / sqrt(My) * exp(pi*1j * (0 : My-1)' * (rand() - 1/2));
ar = kron(ax, ay);
at = 1 / sqrt(N) * exp(pi*1j * (0 : N-1)' * (rand()));
alpha=sqrt(2)/2*(randn(1,1)+1i*randn(1,1)) ;
if l==1
GL=alpha * sqrt(K/(K+1))* ar * at';
GN=0;
else
GN = GN + alpha * sqrt(1/(K+1)) * ar * at';
end
end
G=sqrt(N*M/L)*(GL+GN);
for l = 1 : Lprime
ax = 1 / sqrt(Mx) * exp(pi*1j * (0 : Mx-1)' * (rand()));
ay = 1 / sqrt(My) * exp(pi*1j * (0 : My-1)' * (rand() - 1/2));
at = kron(ax, ay);
alpha=sqrt(2)/2*(randn(1,1)+1i*randn(1,1)) ;
if l==1
hrL=alpha * sqrt(K/(K+1))* at;
hrN=0;
else
hrN = hrN + alpha * sqrt(1/(K+1))* at;
end
end
hr=sqrt(M/Lprime)*(hrN+hrL);
H = diag(hr') * G;%真实信道
%noise=[1,0.562,0.316,0.178,0.1,0];%分别对应0,5,10,15,20DB
for j=1:length(SNR)
W=[];
for t = 1 : T
w = 1 / sqrt(N) * exp(pi*1j * (0 : N-1)' .* (2*rand(N,1)));
v = 1 / sqrt(N) * exp(pi*1j * (0 : M-1)' .* (2*rand(M,1)));
W = [W; kron(w.', v')];
% n = noise(j)*randn(1,1);
y(t) = awgn(v' * H * w,SNR(j));
end
phi = W * F_hat;
x = CS_OMP(y.',phi, L * Lprime);
Sigma = reshape(x, MG, NG);
H_est = Du * Sigma * FL';
NMSE(count,j) = (norm(H_est - H, 'fro') / norm(H,'fro'))^2;
%传统LS估计，这一块有独立的时长
T_1=N*M;
y1=zeros(T_1,1);
Wv=[];
for i=1:T_1
v=exp(1i*pi.*(rand(M,1)-0.5));
w=exp(1i*pi.*(rand(N,1)-0.5));%预编码向量
W=kron(w.',v');
Wv=[Wv;W];
y1(i)=awgn(v'*H*w,SNR(j));
end
tempel_H_LS=inv(Wv)*y1;
H_LS=reshape(tempel_H_LS,M,N);
NMSE1(count,j)=(norm(H_LS - H, 'fro') / norm(H,'fro'))^2;
end
count=count+1
end
NMSE_OMP=sum(NMSE(find(NMSE(:,9)<0.09),:))/length(find(NMSE(:,9)<0.09));%找最优的结果
NMSE_LS=sum(NMSE1(find(NMSE1(:,1)<0.01),:))/length(find(NMSE1(:,1)<0.01));%找最优的结果
semilogy(SNR,NMSE_OMP,'-ro');
hold on;
semilogy(SNR,NMSE_LS,'-b>');
hold off;
认识5G(一)：5G 单天线阵面Type I码本（Type I Single Panel codebook）生成过程_举熙熙然回巧献计的博客-CSDN博客_5g type1码本
【通信】盖氏圆盘方法（GDE）计算均匀直线阵（ULA）中信号源个数附matlab代码 - matlab工作室 - 博客园
阵列天线方向图合成（线阵、面阵）-附Python代码_虾米小飞的博客-CSDN博客_python阵列天线方向图
毫米波信道建模笔记_Vunerable的博客-CSDN博客_功率时延谱