Adapative Instance Normalize

1. AdaIN简介2. 相关工作与背景2.1 批归一化 Batch Normalization2.2 实例归一化 Instance Normalization2.3 条件实例归一化 Conditional Instance Normalization 3. AdaIN（自适应实例规范化）4. 模型构建4.1 结构4.2 训练 5. PyTorch实现6. 实验结果

1. AdaIN简介

使用GAN进行图像风格迁移，网络通常与固定的风格集相关联，无法适应任意新的风格。AdaIN首次实现了任意风格的实时传输。其方法的核心是一个新的自适应实例归一化（AdaIN）层，它将内容特征的均值和方差与样式特征的均值与方差对齐。与现有最快方法相当的速度，不受预定义样式集的限制。此外，允许灵活的用户控制，如内容风格权衡、风格插值、颜色和空间控制，所有这些都使用单个前馈神经网络。

2. 相关工作与背景

2.1 批归一化 Batch Normalization

Batch Normalization层最初设计用于加速区分网络的训练，但也被发现在生成图像建模中有效。

给定Batch输入 x ∈ R N × C × H × W x \in \mathbb{R}^{N \times C \times H \times W} x∈RN×C×H×W, Batch Normalization标准化每个通道的均值和标准差。

B N ( x ) = γ ( x − μ ( x ) σ ( x ) ) + β BN(x) = \gamma\left( \frac{x-\mu(x)}{\sigma(x)}\right)+\beta BN(x)=γ(σ(x)x−μ(x)​)+β γ \gamma γ、 β \beta β是从数据中学习到的仿射参数 μ ( x ) , σ ( x ) \mu(x),\sigma(x) μ(x),σ(x)是针对每个特征通道独立计算的批次大小和空间尺寸的平均值和标准差

2.2 实例归一化 Instance Normalization

在原始方法中，风格迁移网络在每个卷积层之后都包含BN层。但是用Instance Normalization层代替BN层可以实现显著改善性能。

I N ( x ) = γ ( x − μ ( x ) σ ( x ) ) + β IN(x) = \gamma\left( \frac{x-\mu(x)}{\sigma(x)}\right)+\beta IN(x)=γ(σ(x)x−μ(x)​)+β不同于BN，这里的均值和标准差是对于每个通道和每个样本，跨空间维度独立重新计算得到的。 μ n c ( x ) = 1 H W ∑ h = 1 H ∑ w = 1 W x n c h w \mu_{nc}(x)=\frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw} μnc​(x)=HW1​∑h=1H​∑w=1W​xnchw​ σ n c ( x ) = 1 H W ∑ h = 1 H ∑ w = 1 W ( x n c h w − μ n c ( x ) ) 2 + ϵ \sigma_{nc}(x)=\sqrt{\frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_{nc}(x))^2+\epsilon} σnc​(x)=HW1​∑h=1H​∑w=1W​(xnchw​−μnc​(x))2+ϵ ​

2.3 条件实例归一化 Conditional Instance Normalization

一个风格转换网络的所有卷积权重可以在许多风格中共享，而且在归一化之后为每种风格调整仿生变换的参数就足够了 C I N ( x ; s ) = γ s ( x − μ ( x ) σ ( x ) ) + β s CIN(x;s) = \gamma^s\left( \frac{x-\mu(x)}{\sigma(x)}\right)+\beta^s CIN(x;s)=γs(σ(x)x−μ(x)​)+βs γ s \gamma^s γs和 μ s \mu^s μs是针对每一种风格学习得到的仿射参数由于条件实例归一化只作用于缩放和移动参数，在N种风格上训练一个风格转移网络需要的参数比训练N个独立网络的朴素方法要少

3. AdaIN（自适应实例规范化）

A d a I N ( x , y ) = σ ( y ) ( x − μ ( x ) σ ( x ) ) + μ ( y ) AdaIN(x,y) = \sigma(y)\left( \frac{x-\mu(x)}{\sigma(x)}\right)+\mu(y) AdaIN(x,y)=σ(y)(σ(x)x−μ(x)​)+μ(y)AdaIN接收内容输入x和风格输入y，并简单地对齐x的通道平均值和方差以匹配y的值。与BN、IN或CIN不同，AdaIN没有可学习的仿射参数。相反，它从样式输入自适应地计算仿射参数其中，用σ（y）缩放归一化内容输入，并用µ（y）移位。与IN中类似，这些统计数据是跨空间位置计算的

直观地说，考虑一个检测特定风格笔画的特征通道。具有此类笔划的样式图像将产生此功能的高平均激活。AdaIN生成的输出将具有与此功能相同的高平均激活，同时保留内容图像的空间结构。可以使用前馈解码器将笔画特征反转到图像空间。该特征通道的变化可以编码更细微的风格信息，这些信息也被传输到AdaIN输出和最终输出图像。

简言之，AdaIN通过传递特征统计量，特别是信道均值和方差，在特征空间中进行风格传递。

4. 模型构建

4.1 结构

该风格迁移网络T将内容图像c和任意风格图像s作为输入，并合成输出图像，该输出图像将前者的内容和后者的风格重新组合。采用了一种简单的编码器-解码器架构，其中编码器f固定在预训练VGG-19的前几层。在特征空间中对内容和风格图像进行编码之后，将两个特征映射送到AdaIN层，AdaIN层将内容特征映射的均值和方差与风格特征映射的平均和方差对齐，产生目标特征映射t。
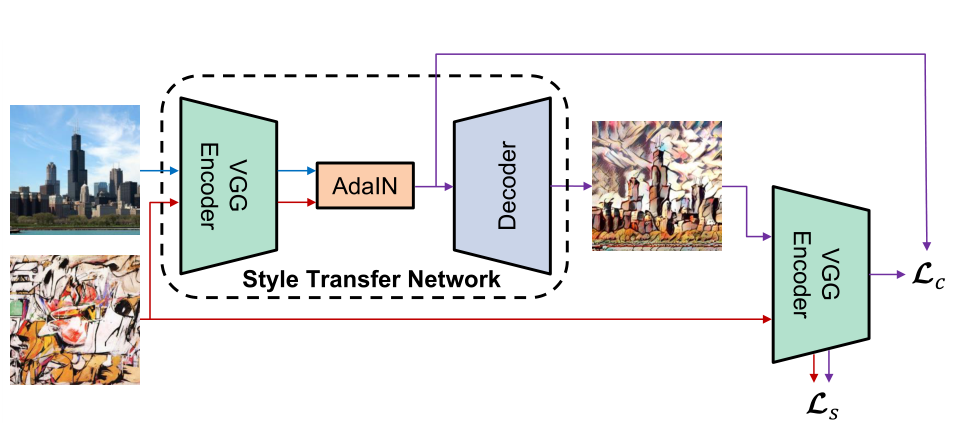
t = A d a I N ( f ( c ) , f ( s ) ) t=AdaIN(f(c),f(s)) t=AdaIN(f(c),f(s))训练随机初始化的解码器g以将t映射回图像空间，生成风格化图像
T ( c , s ) = g ( t ) T(c,s)=g(t) T(c,s)=g(t)解码器主要镜像编码器，所有pooling层由最近的上采样代替，以减少棋盘效应。在f和g中使用反射填充以避免边界伪影。在解码器中不使用归一化层。

4.2 训练

使用Adam优化器，batch大小为8个内容样式图像对。在训练过程中，首先将两幅图像的最小维数调整为512，同时保留纵横比，然后随机裁剪大小为256×256的区域。由于网络是完全卷积的，因此在测试期间可以应用于任何大小的图像。

使用预训练的VGG19来计算训练解码器的损失函数：
L = L c + λ L s L = L_c + \lambda L_s L=Lc​+λLs​ L c = ∥ f ( g ( t ) − t ∥ 2 L_c = \begin{Vmatrix}f(g(t)-t\end{Vmatrix}_2 Lc​=∥ ∥​f(g(t)−t​∥ ∥​2​ L s = ∑ i = 1 L ∥ μ ( ϕ i ( g ( t ) ) ) − μ ( ϕ i ( g ( s ) ) ) ∥ 2 + ∑ i = 1 L ∥ σ ( ϕ i ( g ( t ) ) ) − σ ( ϕ i ( g ( s ) ) ) ∥ 2 L_s=\sum_{i=1}^L\begin{Vmatrix}\mu(\phi_i(g(t)))-\mu(\phi_i(g(s)))\end{Vmatrix}_2+ \sum_{i=1}^L\begin{Vmatrix}\sigma(\phi_i(g(t)))-\sigma(\phi_i(g(s)))\end{Vmatrix}_2 Ls​=∑i=1L​∥ ∥​μ(ϕi​(g(t)))−μ(ϕi​(g(s)))​∥ ∥​2​+∑i=1L​∥ ∥​σ(ϕi​(g(t)))−σ(ϕi​(g(s)))​∥ ∥​2​，用以计算每层上特征的均值和标准差的损失

5. PyTorch实现

6. 实验结果