Python快速构建神经网络
一、前言
机器学习一直是Python的一大热门方向,其中由神经网络算法衍生出来的深度学习在很多方面大放光彩。那神经网络到底是个个什么东西呢?
说到神经网络很容易让人们联想到生物学中的神经网络,而且很多时候也会把机器学习的神经网络和生物神经网络联系起来。但是其实人类至今都没有完全理解生物神经网络的运作,更不要谈用计算机实现生物神经网络了。
相比之下,机器学习中的神经网络更像是一个数学函数。我们输入一组数据,然后神经网络会给我们返回一个结果。像下面这个简单的函数:
y
=
w
x
+
b
(
w
和
b
是
常
数
)
y = wx + b(w和b是常数)
y=wx+b(w和b是常数)
我们给定一个x,就能得到一个y。只不过神经网络的函数要比上面的函数复杂得多。
不过其实神经网络的基础就是上面的函数。下面我们就带大家快速搭建一个神经网络。
二、机器学习
在学习神经网络之前,我们需要了解一些机器学习的知识。
2.1、什么是机器学习?
假如我有下面一组数据:
1, 3, 5, 7, 9
现在让你说出下一个数字可能是什么。
对于人类智慧来说,我们可以很快地说出11。但是对计算机来说却不是那么简单,因为计算机是不会思考的。那计算机要怎么学习呢?这就需要人来指引了。
在机器学习中,人类需要告诉机器如何学习。然后通过人类告诉的学习方法来学习,并得到一个模型。
当然机器学习还有其它一些形式,我们不继续讨论。
2.2、如何学习?
对于机器学习来说,如何学习是一个非常重要的问题。其中已经出现了许多优秀的算法,这些算法的作用都是告诉机器如何学习。比如线性回归、逻辑回归、K近邻、决策树、神经网络等。
机器学习算法可以说是机器学习的灵魂。我们今天要实现的神经网络也是一种机器学习算法,他是建立在逻辑回归的基础之上的,而逻辑回归又建立在线性回归之上。因此线性回归和逻辑回归也是今天要学习的内容。
2.3、机器学习中的问题
机器学习的问题通常分为两大类,一个类是分类,一类是回归。
它们两者的区别是结果是否离散。比如一个动物分类问题,我们得到的结果只可能是一个确定的动物。不会得到一个介于猫狗之间的动物。
而回归问题的结果通常是一个数值,比如房价预测问题。我们可能得到0-100万之间任意一个数值,也可能得到一个类似40.023242的小数。
其中线性回归就是解决回归问题的一大利器,而逻辑回归则是用于分类问题。下面我们就来看看这两个算法。
三、线性回归和逻辑回归
可能你会好奇,为什么逻辑回归名字里有个回归却是不是解决回归问题的。相信看完下面的内容就不会有这个疑惑了。
3.1、线性回归
在前言中,我们介绍了一个简单的函数:
y
=
w
x
+
b
y = wx + b
y=wx+b
其实它就是线性回归的基础。线性回归算法就是找到一组最优的w b,让我们得到最接近真实的结果。我们还是用上面的数据:
1, 3, 5, 7, 9
对于上面这组数据,我们是要找序号和数值之间的关系,我们可以把上面的数据理解为:
x, y
1, 1
2, 3
3, 5,
4, 7,
5, 9
其中x表示需要,y表示具体的数值。我们稍加运算就可以得到下面这个函数:
y
=
2
x
−
1
y = 2x - 1
y=2x−1
我们得到了最优的一组参数w=2, b = -1,通过这个函数我们就可以预测后面后面一千、一万个数字。
不过有时候我们会有多个x,这时我们就可以把上面的函数推广为:
y
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
n
x
n
+
b
y = w_1x_1 + w_2x_2 + ...+w_nx_n + b
y=w1x1+w2x2+...+wnxn+b
这时候我们需要求得参数就多多了。下面我们来实际写一个线性回归的程序。
3.2、线性回归实战
这里我们需要使用到scikit-learn模块,安装如下:
pip install scikit-learn
然后我们就可以开始写代码了。线性回归算法的实现被封装在了sklearn.linear_model中的LinearRegression,我们可以直接使用:
import numpy as np
from sklearn.linear_model import LinearRegression
# 准备x的数据
X = np.array([
[1],
[2],
[3],
[4],
[5]
])
# 准备y的数据
y = np.array([1, 3, 5, 7, 9])
# 创建线性回归模块
lr = LinearRegression()
# 填充数据并训练
lr.fit(X, y)
# 输出参数
print("w=", lr.coef_, "b=", lr.intercept_)
首先我们需要准备X和y的数据,这里我们使用的是ndarray数组。这里需要注意,我们y的的数据长度为5,则X的数据需要是5*n。
准备好数据后我们需要创建线性回归模型,然后调用fit方法填充我们准备好的数据,并训练。
训练完成后我们可以查看一下模块的参数,其中coef_表示w,而intercept_表示b。因为w可以有多个,所以它应该是个数组,下面是输出结果:
w= [2.] b= -1.0
和我们人工智慧得到的结果是一样的。我们还可以调用predict方法预测后面的数据:
import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([
[1],
[2],
[3],
[4],
[5]
])
y = np.array([1, 3, 5, 7, 9])
lr = LinearRegression()
lr.fit(X, y)
y_predict = lr.predict(np.array([[100]]))
print(y_predict)
这里同样需要注意X的数据是二维的。
3.3、逻辑回归
逻辑回归可以理解为线性回归+特殊函数。我们可以思考下面这个问题。
现在需要写一个程序来判断每个人的分数是否及格,计分标准为:总分=40%数学+30%语文+30%英语。总分大于等于60为及格,其余为不及格。
虽然是个很简单的问题,但是我们还是需要讨论一下。首先我们可以把计算总分的公式写成下面的形式:
y
=
0.4
x
1
+
0.3
x
2
+
0.3
x
3
+
b
y = 0.4x_1 + 0.3x_2 + 0.3x_3 + b
y=0.4x1+0.3x2+0.3x3+b
对于这个公式,我们可以得到0-100之间的任何一个数字。但是我想要得到的只有两个结果,及格或者不及格。我们可以简单理解为-1和1。
那我们怎么把上面的结果映射到-1和1上呢?这就需要使用一个特殊的函数了,我们把这个函数叫做激活函数。我们可以用下面这个函数作为激活函数:
f
(
x
)
=
y
−
60
∣
y
−
60
∣
f(x) = \frac{y-60}{|y-60|}
f(x)=∣y−60∣y−60
这样就可以把所有分数映射到-1和1上了。(上面的函数在y=60处无定义,严格上来讲上面的激活函数是不适用的)逻辑回归的图示如下:
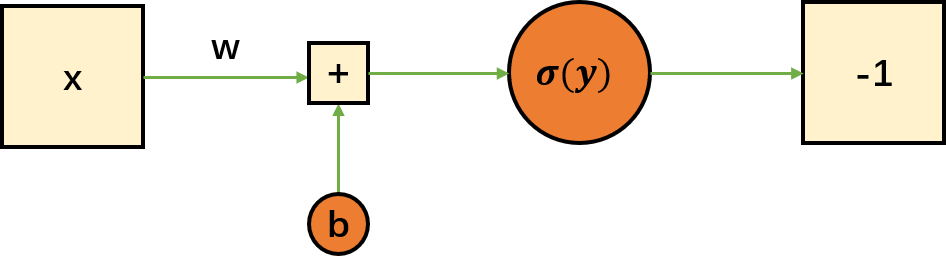
先通过一个线性模型得到一个结果,然后再通过激活函数将结果映射到指定范围。
不过在实际应用中,我们通常会使用Sigmoid、Tanh和ReLU函数。下面是几个激活函数的图像:
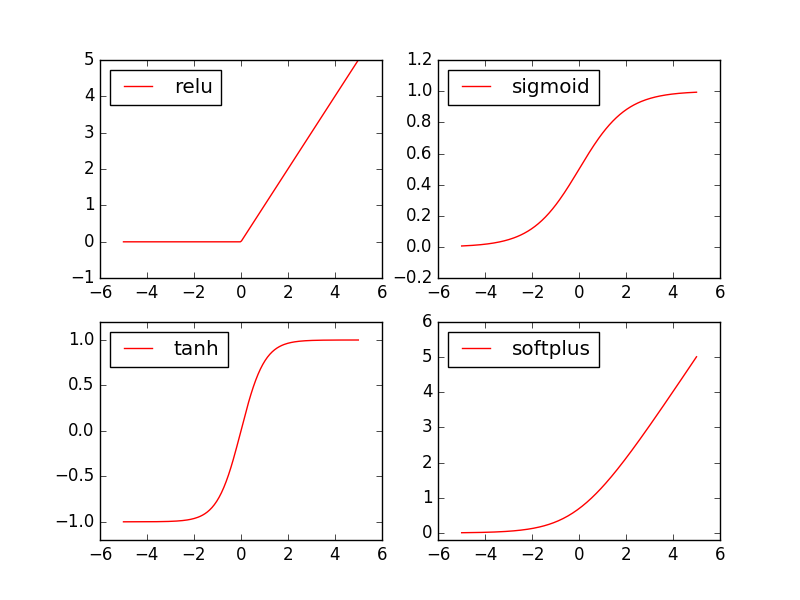
下面我们来写一个逻辑回归的例子。
3.4、逻辑回归实战
我们用逻辑回归解决是否几个的问题,逻辑回归的实现封装在linear_model.LogisticRegression中,同样可以直接使用,我们直接上代码:
import numpy as np
from sklearn.linear_model import LogisticRegression
# 准备X的数据
X = np.array([
[60],
[20],
[30],
[80],
[59],
[90]
])
# 准备y的数据
y = np.array([1, 0, 0, 1, 0, 1])
# 创建逻辑回归模型
lr = LogisticRegression()
# 填充数据并训练
lr.fit(X, y)
# 准备用于测试的数据
X_test = np.array([
[62],
[87],
[39],
[45]
])
# 判断测试数据是否及格
y_predict = lr.predict(X_test)
print(y_predict)
代码和线性回归只有一些细微的差别。在代码中,我们用0表示不及格,1表示及格。下面是我们测试数据输出的结果:
[1 1 0 0]
可以看到所有结果都预测正确了。
有了上面的知识,我们就可以开始实现一个神经网络了。
四、神经网络
神经网络是建立在逻辑回归之上的,可以说神经网络就是一个逻辑回归的集合。
4.1、神经网络
想必大家都听说过,神经网络是由大量的神经元组成的。不过你可能不知道,机器学习中的神经元就是我们前面学的逻辑回归。我们可以看下面这张图:

可以看到和之前的逻辑回归很像,但是这里使用了很多激活函数,而且参数数量也要多得多。
至于为什么要使用这么多激活函数可以说就是为了让得到的函数非常复杂。如果我们的函数非常简单,比如下面这组数据:
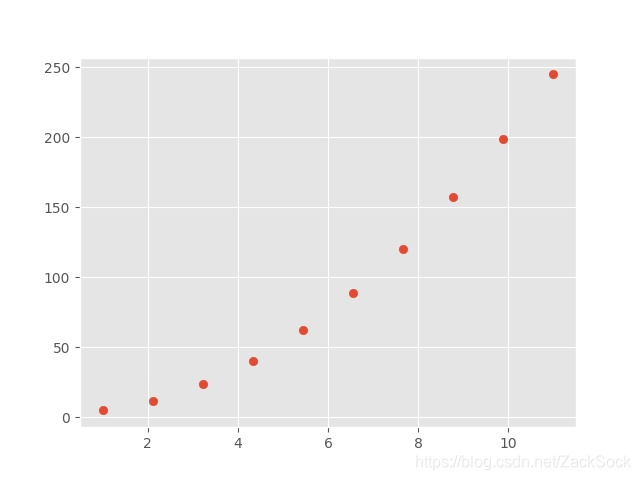
假如用下面的函数作为我们的模型:
y
=
w
x
+
b
y = wx + b
y=wx+b
会得到下面这张图像:
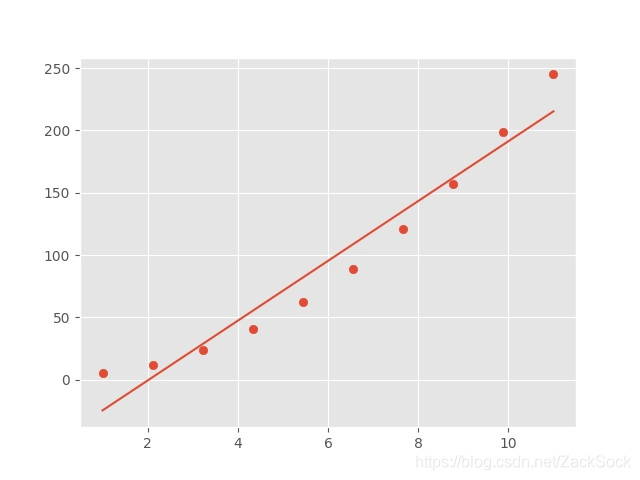
可以看到有许多点都不在直线上,所以预测的数据会有很多误差。这个时候我们可以考虑二次,如:
y
=
w
x
2
+
b
y = wx^2 + b
y=wx2+b
但是有时候二次、三次、甚至十几次都无法得到我们想要的模型(次数过多往往会出现过拟合现象)。这个时候神经网络就是一个很好的选择。
神经网络的可解释性比之前两个算法要差得多,因为神经网络通常有成百上千个参数,我们会得到一个非常复杂的模型。虽然不能理解参数的含义,但是这些参数通常会给我们一个很好的结果。不过这也真是神经网络的神奇之处。
4.2、输入层、隐层、输出层
神经网络通常会有三个部分,输入层由我们的特征数决定。而输出层由我们分类数量决定,如图x部分为输入层,y部分为输出层,而中间部分为隐藏层:

隐藏层通常会特别复杂,我们可以通过调节隐层的层数和节点数来调整模型的复杂度。
4.3、神经网络实战
使用scikit-learn,我们可以很快搭建一个神经网络。接下来我们用scikit-learn中自带的数据集来实现一个神经网络:
from sklearn.datasets import load_iris
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
# 加载数据集
iris_data = load_iris()
# 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(iris_data['data'], iris_data['target'], test_size=0.25, random_state=1)
# 创建神经网络模型
mlp = MLPClassifier(solver='lbfgs', hidden_layer_sizes=[4, 2], random_state=0)
# 填充数据并训练
mlp.fit(X_train, y_train)
# 评估模型
score = mlp.score(X_test, y_test)
print(score)
这里我们使用的是scikit-learn自带的鸢尾花数据,我们用train_test_split将数据集分割成了两个部分,分别是训练集的特征和目标值,以及测试集的特征和目标值。
然后我们创建MLPClassifier类的实例,实际上它就是一个用于分类的多重感知机。我们只需要关注hidden_layer_sizes参数即可,它就是我们神经网络的层数和节点数。因为是一个二分类问题,所以这里的输出层有两个节点。
下面输出的结果:
0.9210526315789473
我们调用mlp.score评估模型的好坏,92%的准确率也算是一个非常优秀的结果了。