文章目录

Matlab异常值处理异常值的识别方法数据给定范围数据没有给定范围3sigma原则箱线图识别异常值 去除异常值后咋办

Matlab异常值处理

在对数据进行预处理中，我们经常会遇到异常值和缺失值的情况，下面我们对这两种情况的常用技术进行介绍，希望能帮到大家。

在数据既有异常值又有缺失值时，先处理哪个并没有严格的顺序。我习惯先处理异常值，再处理缺失值

异常值的识别方法

异常值，指的是样本中的一些数值明显偏离其余数值的样本点，所以也称为离群点。常见的异常值判断方法可以分为以下两种情况：

数据给定范围

数据没有给定范围

3sigma原则

前提是要正态分布，才可以用3sigma原则确定异常值。 历史经验：身高统计：正态性检验 如果要缩小一点区间，多去除一些异常值 可以用2sigma

x = [48 51 57 57 49 86 48 53 59 50 48 47 53 56 60];   % 假设x是取自正态分布的样本u = mean(x,'omitnan');  % 忽略数据中的缺失值计算均值sigma = std(x,'omitnan');   % 计算标准差  std(x,0,'omitnan')是总体标准差lb = u - 3*sigma    % 区间下界，low bound的缩写ub = u + 3*sigma   % 区间上界，upper bound的缩写tmp = (x < lb) | (x > ub);ind = find(tmp)

返回6，意味着第6个位置是异常值

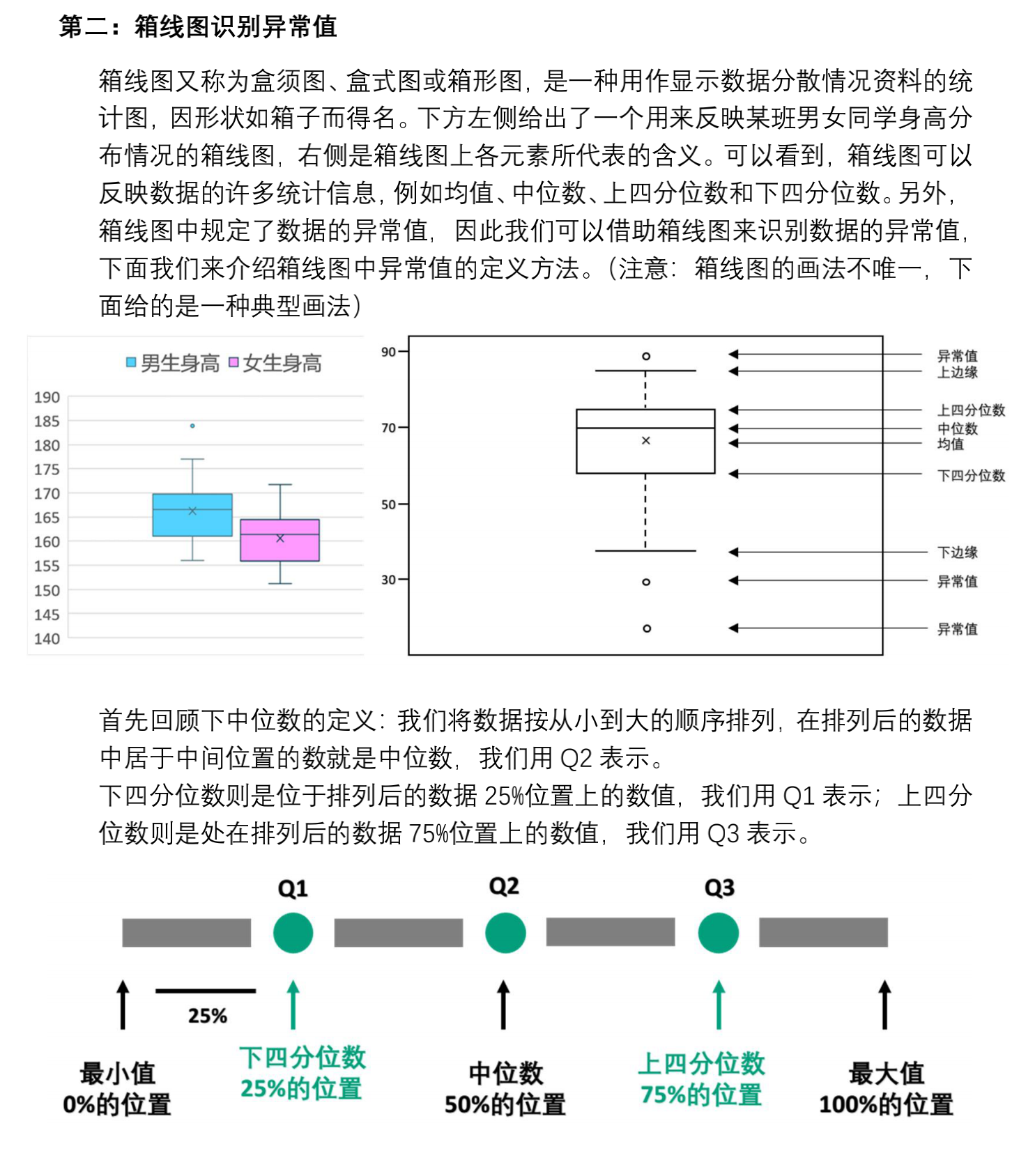
通常不知道总体是否是正态分布的时候，我们用箱线图来去除异常值通常来说箱线图比3sigma去除的异常值要多通常k取1.5，当然也可以取其他的

箱线图识别异常值

x = [48 51 57 57 49 86 48 53 59 50 48 47 53 56 60];% 计算分位数的函数需要MATLAB安装了统计机器学习工具箱Q1 = prctile(x,25); % 下四分位数Q3 = prctile(x,75); % 上四分位数IQR = Q3-Q1; % 四分位距lb = Q1 - 1.5*IQR % 下界ub = Q3 + 1.5*IQR % 上界tmp = (x < lb) | (x > ub);ind = find(tmp)

去除异常值后咋办

识别出异常值后，我们通常可以将异常值视为缺失值，然后交给缺失值处理方法来处理。

代码：x(ind) = nan （注意：如果有多列数据都需要处理，可以写一个循环。）

x(ind) = nan % 这里的nan表示非数字Not-a-Number,例如0/0就会返回nan，我们这里可以用nan代表数字中的缺失值

如果数据给定范围，那么很容易找到异常值如果数据没给定范围，那么一般偷懒不做 除非数据很离谱，或者影响了模型的训练效果