无论哪个深度学习框架，它的张量类（PyTorch中为Tensor）都和Numpy的ndarray类似，接下来介绍的很多函数名和Numpy中的都一样，不过会比Numpy的ndarray多一些重要功能，比如张量类支持自动微分。

数据操作

创建数据

import torch
#默认创建为浮点数
x = torch.arange(12)
#访问张量的形状（沿每个轴的长度）
x.shape
#改变形状
x.reshape(3,4)
#全0初始化矩阵
torch.zeros((2,3,4))
#全1初始化矩阵
torch.ones((2,3,5))
#指定特定分布，均值为0、标准差为1的标准高斯分布
torch.randn(3,4)
#可直接为张量中的元素赋予确定值
torch.tensor([[2,1,3],[2,5,6],[8,3,1]])

Out:

数据运算

x = torch.tensor([1,2,3,4])
y = torch.tensor([3,4,9,5])
#按元素计算
print("x*y:",x*y)
print("exp:",torch.exp(x))

Out:

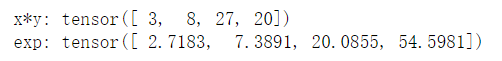
连结concatenate这个概念是比较常见的，SQL中，Dataframe中都很常见，我们也可以把多个张量连结在一起，在连结的时候需要给出沿哪个轴连结。

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
print("X:",X)
print("Y:",Y)
print("沿轴-0连结矩阵：")
torch.cat((X,Y), dim=0)
print("沿轴-1连结矩阵：")
torch.cat((X,Y), dim=1)

Out:

降维求和

X
X.sum(axis=0)
X.sum(axis=1)
X.sum(axis=[0,1])
X.mean()
X.numel()

Out:

非降维求和

X.sum(axis=1,keepdims=True)
X.sum(axis=1)

Out:

点积

x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype=torch.float32)
torch.dot(x,y)

Out:

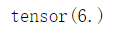
矩阵-向量积

A
x
torch.mv(A,x)

矩阵-矩阵乘法

A = torch.ones(3,4)
B = torch.arange(12, dtype=torch.float32).reshape((4,3))
A
B
torch.mm(A,B)

索引和切片

#选择最后一个元素
X[-1]
#切片
X[1:3]
#可通过指定索引更改元素
X[1,2] = 100
X
X[2,:] = 50 
X

Out:

转换数据类型

A = X.numpy()
B = torch.tensor(A)
print("A的类型为：",type(A))
print("B的类型为：",type(B))

Out:

微分

在深度学习中，通常选择对于模型参数可微的损失函数。
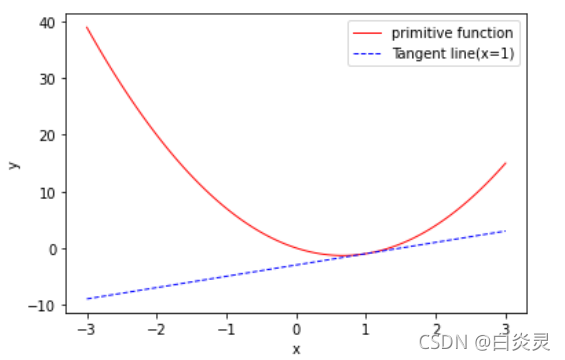
定义 u = f ( x ) = 3 x 2 − 4 x u=f(x)=3x^{2}-4x u=f(x)=3x2−4x

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(-3,3,100)
def f(x):
    return 3*x**2 - 4*x
def g(x):
    return 2*x - 3
plt.plot(x,f(x),color='red',linewidth=1.0,label="primitive function")
plt.plot(x,g(x),color='blue',linewidth=1.0,linestyle='--',label="Tangent line(x=1)")
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc="best")

# 显示图像
plt.show()

自动求导

自动求导可以使系统能够随后反向传播梯度（backpropagate）。

import torch
x = torch.arange(4.0,requires_grad=True)
print(x.grad)
#调用反向传播函数来自动计算y关于每个分量的梯度
y = 2*torch.dot(x,x)
y.backward()
print(x.grad)
#验证梯度是否正确计算
x.grad == 4*x

Out:

#默认情况下，PyTorch会累积梯度
x.grad.zero_()
y = x.sum()
y
y.backward()
x.grad

Out:

PyTorch基础系列的学习资料为：

1. 莫烦大神的PyTorch视频教程
2. 《Dive Into Deep Learning》
3. PyTorch官方文档