目录
前言
一、多维数组
1.多维数组定义及顺序存储
1.1 多维数组的定义
1.2 数组的顺序存储
2.矩阵的压缩存储
2.1 特殊矩阵
2.2 稀疏矩阵
二、广义表
1.广义表基础
1.1 广义表的定义
1.2 广义表的存储结构
前言
多维数组和广义表是一种复杂的非线性结构,它们的逻辑特征是:一个数据元素可能有多个直接前趋和直接后继。
多维数组可以看成是线性表的推广。因为一旦确定数组是按行或按列优先顺序存储之后,每个数组元素之间的关系就同一维数组一样变成线性的了。因此,只要弄清楚多维数组按行优先顺序存储结构之后,它的运算就同线性表的运算类似。

一、多维数组
1.多维数组定义及顺序存储
1.1 多维数组的定义
数组是我们比较熟悉的一种数据类型。由于数组中各元素具有相同的数据类型,并且数组元素的下标一般具有固定的上界和下界,因此,数组的处理比其他复杂的结构较为简单。当数组维数为1时,数组是一种元素个数固定的线性表,而维数大于1时,称为多维数组,它可以看成是线性表的推广。这里仅讨论多维数组。
由于对数组一般不做插入和删除操作,因此数组一旦建立,结构中的元素个数和元素间的关系就不再发生变化。所以,一般都是采用顺序存储的方法来表示数组。
多维数组是一种复杂的数据结构。以二维数组为例,数组元素之间的关系除了边界元素外,每个元素都恰好有两个直接前趋和两个直接后继:行向量上的直接前趋是
和
,列向量上的直接前趋是
和直接后继
。并且二维数组也只有一个开始结点
,它没有前趋;仅有一个终端结点
,它没有后继。此外,边界上的结点(开始结点和终端结点除外)只有一个直接前趋或者只有一个直接后继。
1.2 数组的顺序存储
(1)按行优先顺序存储,即将数组元素按行向量排列,第i+1个行向量紧接在第i个行向量后面。A的m x n个元素按行优先顺序存储的线性序列为:
(2)按列优先顺序存储,即将数组元素按列向量排列,第j+1个列向量紧接在第j个列向量之后, A的m x n个元素按列优先顺序存储的线性序列为:
如果按上述两种方式顺序存储数组,只要知道开始结点的存储地址(即基地址),维数和每维的上、下界,以及每个元素所占用的单元数,就可以将每个数组元素的存储地址表示为其下标的线性函数。
在C语言中的数组元素的地址计算函数为:
2.矩阵的压缩存储
2.1 特殊矩阵
所谓特殊矩阵,指的是相同值的元素或者零元素在矩阵中的分布有一定规律的矩阵。
2.1.1 对称矩阵
若n阶方阵A中的元素满足下述性质:
则称A为n阶的对称矩阵。对称矩阵中的元素是关于主对角线对称的,所以只需要存储矩阵上三角或下三角的元素即可,让两个对称的元素共享一个存储空间。

2.1.2 三角矩阵
以主对角线划分,三角矩阵有上三角和下三角两种。上三角矩阵是指矩阵的下三角(不包括对角线)中的元素均为常数c或是零的n阶方阵,如图4.3(b)所示;下三角矩阵正好相反,它的主对角线上方均为常数c或零,如图4.3(a)所示。一般情况下,三角矩阵的常数c均为零。

2.2 稀疏矩阵
由于特殊矩阵中非零元素的分布是有规律的,因此总可以找到矩阵元素与一维数组的下标的对应关系。但还有一种矩阵,其中有s个非零元素,而s远远小于矩阵元素的总数,通常把这种矩阵称为稀疏矩阵,为了节省存储单元,也可用压缩存储方法只存储非零元素。由于稀疏矩阵非零元素的分布一般是没有规律的,因此在存储非零元素时,除了存储非零元素的值之外,还必须同时存储该元素的行、列位置(即下标),所以可用一个称为三元组(i,j,
)来唯一确定一个非零元素。
三元组表:
如果将表示稀疏矩阵非零元素的三元组按行优先的顺序排列,则可得到一个其结点均为三元组的线性表,将这种线性表的顺序存储结构称为三元组表。
二、广义表
1.广义表基础
广义表是线性表的推广,又称列表。线性表的元素仅限于原子项,即每个数据元素只能是一个数或一个记录,如果放松对线性表元素的这种限制,允许它们自身具有结构,由此就产生广义表的概念。
1.1 广义表的定义
广义表是n(n≥0)个元素,
,...,
的有限序列,其中
或者是原子项,或者是一个广义表,通常记作LS=(
,
,...,
)。LS是广义表的名字,n为它的长度。若
又是广义表,则称它为LS的子表。为了区分原子和广义表,在书写时习惯上用大写字母表示广义表,用小写字母表示原子。通常用圆括号将广义表括起来,用逗号分隔其中的元素。当广义表LS非空时, 称第一个元素
是LS的表头(head) , 其余元素组成的表(
,...,
) 称为LS的表尾(tail) 。
1.2 广义表的存储结构
通常采用链式存储结构,每个元素可用一个结点表示,结点结构如下所示:
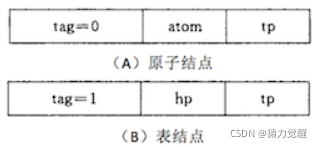
如图所示,表示原子的节点构成由 tag 标记位、原子值和 tp 指针构成,表示子表的节点由 tag 标记位、hp 指针和 tp 指针构成。
博主创作不易,喜欢这篇博客的朋友们点个赞吧!(≧∇≦)ノ