一次性搞懂KMP算法

如果你是想来看为什么k=next[k],可以翻到第二章的情况2去看；如果你是和我一样的萌新小白想了解KMP算法，可以从头读起，了解KMP算法的动机和具体实现原理最后了解其C语言实现细节。

一、动机

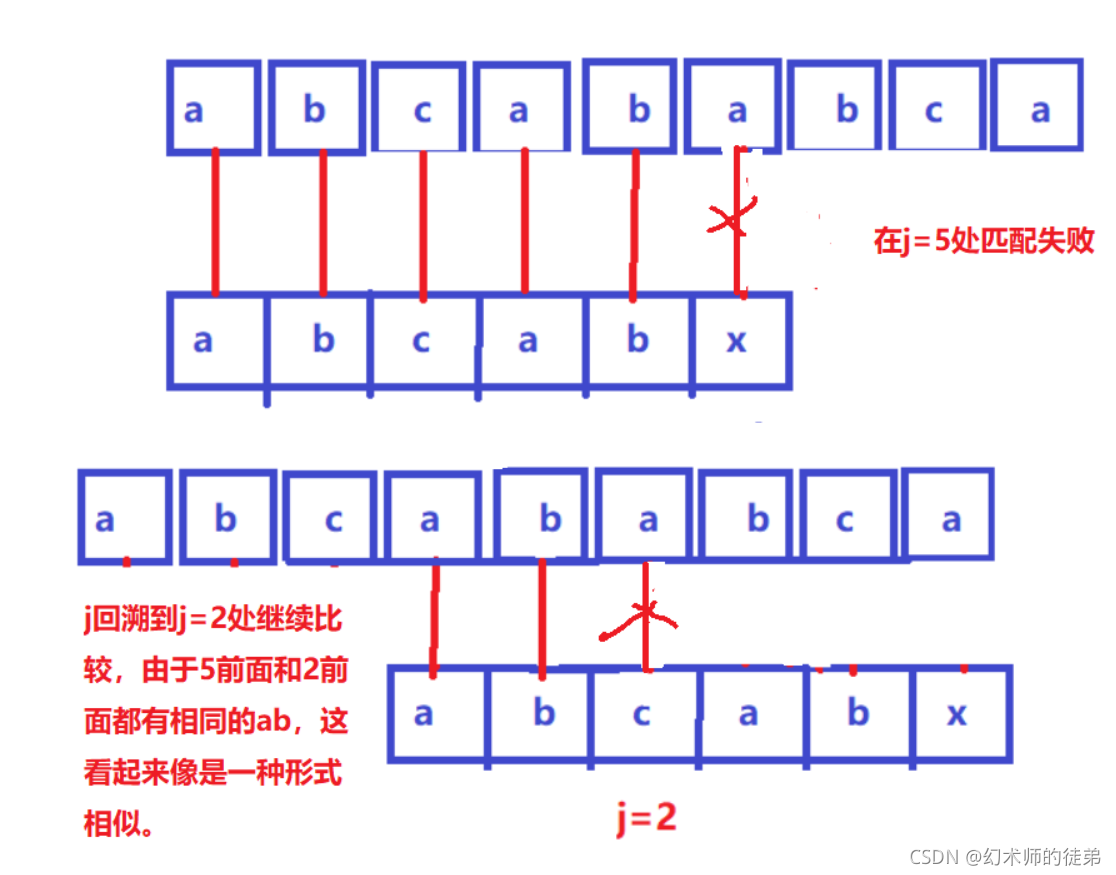
  传统的实现str函数的BF算法会在子串与主串之间存在许多"部分匹配"的情况下有很多没有意义的重复步骤，如下图。

  本文中，主串记为str，在主串中寻找的串记为sub，本文中的子串都是真子串，不包含串本身的子串，也不包含空串,

  sub[0]…sub[k-1]表示由字符sub[0]…sub[k-1]组成的串。

  下图中，i表示用来遍历str的指针的位置；j表示用来遍历sub的指针的位置。

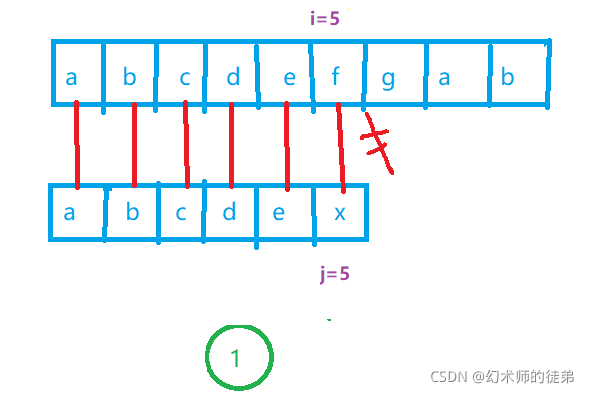
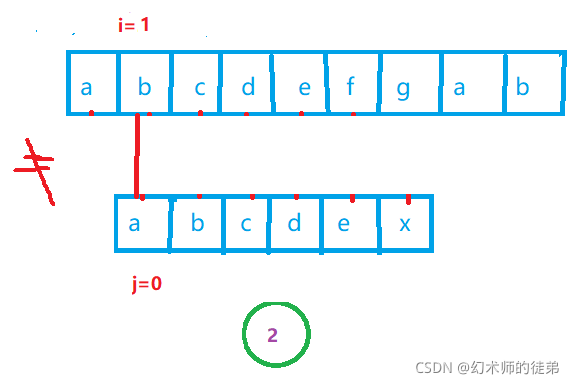
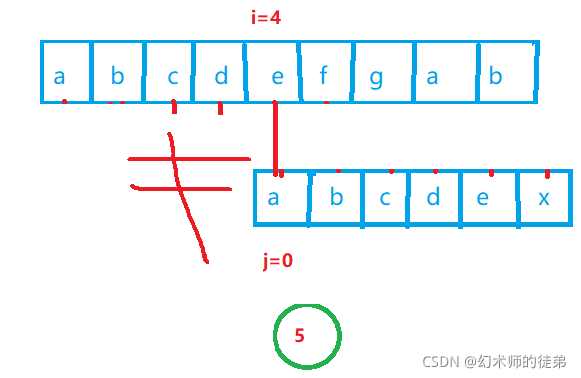
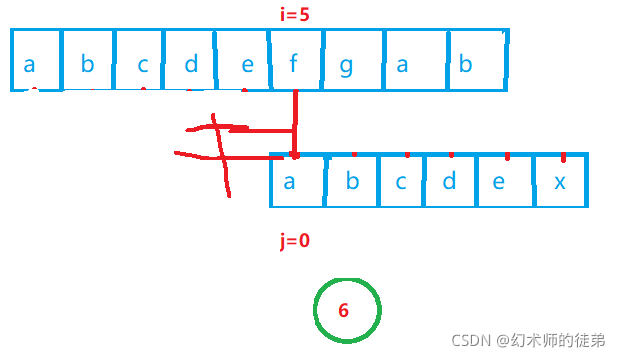
  传统的BF算法当匹配失败时，为了能够遍历str的所有子串，它会让i回溯到此轮比较开始位置的下一个位置，让j回溯到sub的起始位置，继续比较，但是出于一个考虑，这样是没必要的：

  sub它的每一部分都是不相同的,

即
s u b [ 0 ] ! = s u b [ 1 ] , s u b [ 0 ] ! = s u b [ 2 ] , s u b [ 0 ] ! = s u b [ 4 ] sub[0]!=sub[1],sub[0]!=sub[2],sub[0]!=sub[4] sub[0]!=sub[1],sub[0]!=sub[2],sub[0]!=sub[4]
  而我们的第一轮比较一直走到x才结束，这说明str的前五个字符一定和sub是相等的，

即
s t r [ i ] = = s u b [ i ] , f o r ( i = 0 , 1 , 2 , 3 , 4 ) str[i]==sub[i], for(i=0,1,2,3,4) str[i]==sub[i],for(i=0,1,2,3,4)

  那么一定有
s u b [ 0 ] ! = s t r [ 1 ] , s u b [ 0 ] ! = s t r [ 2 ] , s u b [ 0 ] ! = s t r [ 3 ] , s u b [ 0 ] ! = s t r [ 4 ] sub[0]!=str[1],sub[0]!=str[2] ,sub[0]!=str[3] ,sub[0]!= str[4] sub[0]!=str[1],sub[0]!=str[2],sub[0]!=str[3],sub[0]!=str[4]

  这四个不等式说明，我们的比较过程②③④⑤都是没必要的，因为他们早在①中就可以确定一定会匹配失败，但是⑥是不能省略的，因为我们没有判断sub[0]和sub[5]是否相等。

  所以我们希望我们的算法可以直接做到把上面的六步简化为两步。

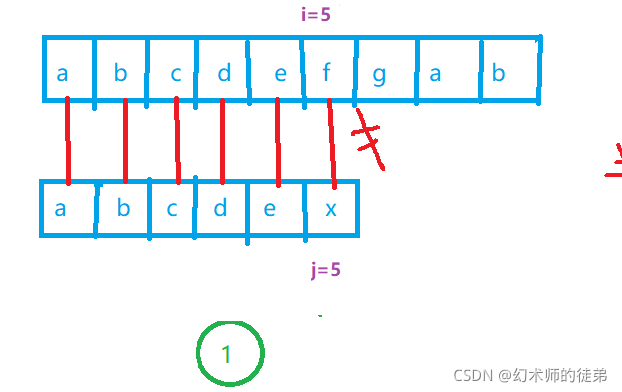
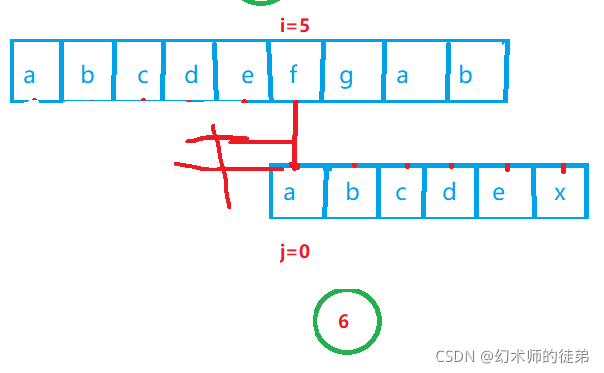
  有人可能会说，啊这是个特例情况，sub串前面都没有相同的字符，那么我们接下来就举一个由相同字符的例子。

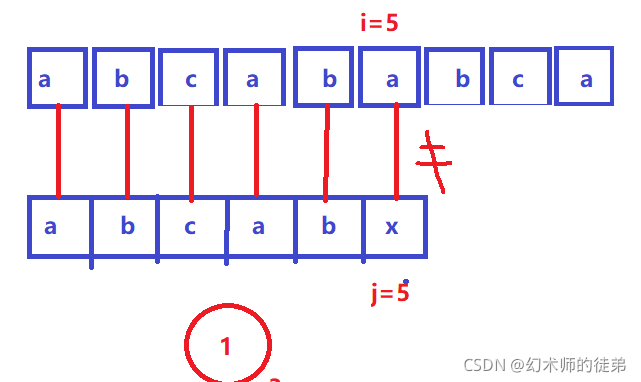
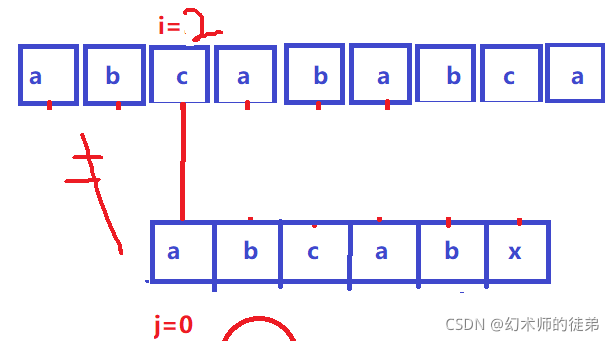
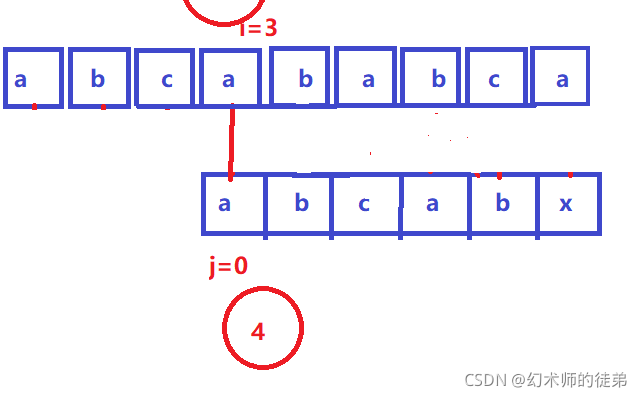
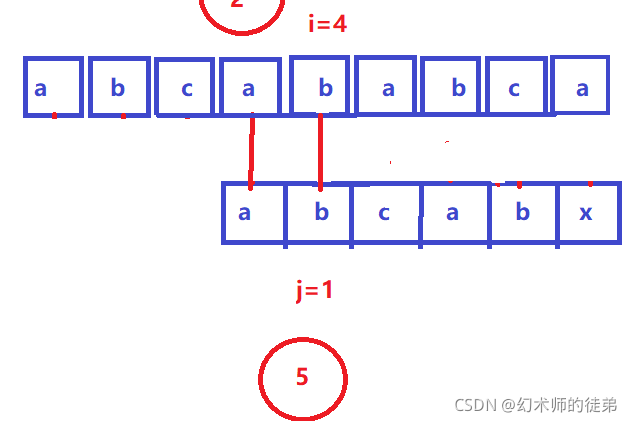
  步骤②③可以省略，因为abc是不相等的字符，原理同上；
  步骤④⑤其实也可以省略，因为我们的sub串中有两个相同的字串sub[0]sub[1]和sub[3]sub[4]，我们 既然已经在步骤①中比较过了sub[3]sub[4]==str[3]str[4]，那sub[0]sub[1]==str[3]str[4]这不是理所应当的吗
  所以我们可以把这六个步骤简化为两个步骤：

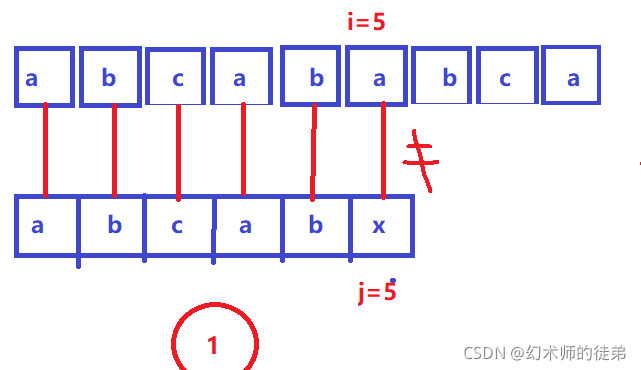
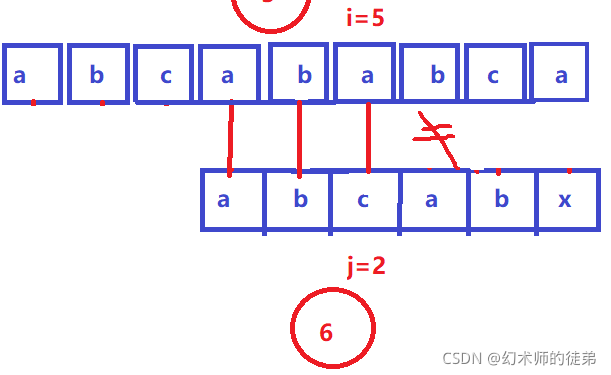
  通过观察这两个例子，我们有一些直观的感受:

• 每次匹配失败后，指向主串str当前位置的指针i没必要回退，这个位置记为位置1
• 因为如果回退了，
  • 假如str(sub因为前面匹配都是成功的 所以这里说这两者任意一个都可以)在匹配失败位置以前的串中没有相同的字符，那会一路匹配失败再回到原本的位置1；
  • 假设sub前面有一系列相同的字符，那会出现一系列匹配失败和部分匹配成功，然后也回到原本匹配失败的位置1。
• 观察发现匹配失败时，指向sub当前匹配位置的指针j要回溯到一个恰当的位置，这个位置由失败位置之前的串的前后缀相似程度就决定(这里的前后缀的意思是以sub[0]开始的串和以sub[失败位置-1]结束的串)。

二、next数组

  下面我们来详细讨论一下j回溯的位置，首先我们观察到j发生回溯是在str和sub匹配失败时，那在失败位置之前的位置str和sub都是匹配成功的(也就是对应字符都是相等的)，因此我们我们的回溯位置仅仅由sub匹配失败位置之前的串决定。

  根据图中的理解，我们寻找回溯位置是遵照了这样一个准则，找一个位置以sub[0]开头的串1，他的结尾字符是sub[j-1]（位置不确定），如果再能找到一个结尾位置是sub[j-1]的串2，并且其开头字符是sub[0]（位置不确定 下标记为x） 且要求这俩串相等的。

  如果能做到这件事情，我们就让j回溯到串1结尾位置的后面的一个位置，我们记这个位置的下标为k,通过串1串2相等，我们计算出x的位置
s u b [ x ] . . . . s u b [ j − 1 ] = = s u b [ 0 ] . . . s u b [ k − 1 ] sub[x]....sub[j-1]==sub[0]...sub[k-1] sub[x]....sub[j−1]==sub[0]...sub[k−1]
⇒ k − 1 − 0 = = j − 1 − x \Rightarrow k-1-0==j-1-x ⇒k−1−0==j−1−x
⇒ x = j − k \Rightarrow x=j-k ⇒x=j−k
这时，在此轮匹配的时候，对匹配失败位置i以前的串有
s t r [ i − k ] . . . s t r [ i − 1 ] = = s u b [ j − k ] . . . . s u b [ j − 1 ] str[i-k]...str[i-1]==sub[j-k]....sub[j-1] str[i−k]...str[i−1]==sub[j−k]....sub[j−1]
因此对我们回溯的k位置，有
( s u b [ j − k ] . . . s u b [ i − 1 ] = = s u b [ 0 ] . . . s u b [ k − 1 ] ) (sub[j-k]...sub[i-1]==sub[0]...sub[k-1]) (sub[j−k]...sub[i−1]==sub[0]...sub[k−1])
∧ ( s t r [ i − k ] . . . s t r [ i − 1 ] = = s u b [ j − k ] . . . . s u b [ j − 1 ] ) \wedge (str[i-k]...str[i-1]==sub[j-k]....sub[j-1]) ∧(str[i−k]...str[i−1]==sub[j−k]....sub[j−1])
⇒ s t r [ i − k ] . . . s t r [ i − 1 ] = = s u b [ 0 ] . . . s u b [ k − 1 ] \Rightarrow str[i-k]...str[i-1]==sub[0]...sub[k-1] ⇒str[i−k]...str[i−1]==sub[0]...sub[k−1]

  我们就回溯到了这样一个位置，他前面的子串(以sub[0]起始)和str中当前匹配位置之前的子串(以str[i-k]起始)是相等的。

  我们用一个数组next来记录匹配失败j应当回溯的位置，next[j]表示在j处匹配失败应该回到的位置

所以，在j处匹配失败后，应当回到的位置是：
n e x t [ j ] = m a x { k ∣ ( 0 < k < j ) ∧ ( s u b [ 0 ] . . . s u b [ k − 1 ] = = s u b [ j − k ] . . . s u b [ j − 1 ] ) } next[j]=max\left\{ k|(0<k<j) \wedge (sub[0]...sub[k-1] ==sub[j-k]...sub[j-1]) \right\} next[j]=max{k∣(0<k<j)∧(sub[0]...sub[k−1]==sub[j−k]...sub[j−1])}
  但是我们忽略了一件事情，如果不存在这样的两个串怎么办，即做不到找到两个相等的子串。

  那这时候，我们应该回溯到下标为0的位置，因为这说明不能通过我们上面的技巧来减少j的遍历次数，所以回到0位置从头开始遍历；

  如果在0位置就匹配失败，我们要让它回溯到-1位置，即next[0]=-1，这种规定是为了方便我们后面写代码好统一两种进入if语句的条件。

  如果是1位置匹配失败，就只有一个字符不存在子串，直接让他回溯到0位置，所以我们规定next[1]=0;

所以next数组的求解公式应该是这样的

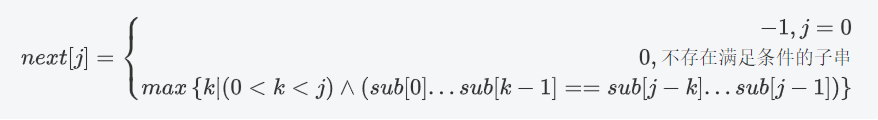
  但是这是一个非常数学的求解公式，我们要转化成一个计算机也能理解的事情，怎么做呢？

  观察下图的next数组：

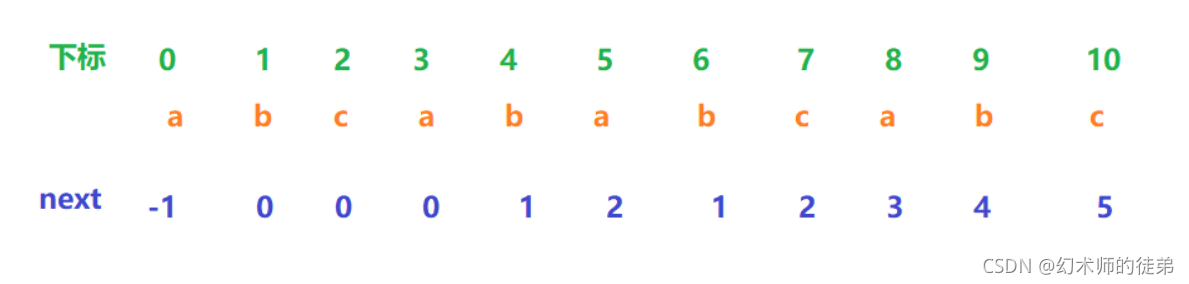
  我们发现next每次增大的话也只能一次增加1，这是自然的，因为每次都只会在后面的子串中多加一个元素，这似乎启发我们从递推的角度去想这个问题.

我们假设
n e x t [ i − 1 ] = = k next[i-1]==k next[i−1]==k
也就是说i-1位置匹配失败时，j的回溯位置是k，

  根据假设 这说明当在i-1位置发生匹配失败时，会回溯到k位置，也就是说，能找到的两个最大相等子串的长度是k，

所以有
s u b [ 0 ] . . . s u b [ k − 1 ] = = s u b [ i − k − 1 ] . . . s u b [ i − 2 ] sub[0]...sub[k-1]==sub[i-k-1]...sub[i-2] sub[0]...sub[k−1]==sub[i−k−1]...sub[i−2]
假设如果有（这种情况记为情况1）
s u b [ k ] = = s u b [ i − 1 ] sub[k]==sub[i-1] sub[k]==sub[i−1]
立即推
s u b [ 0 ] . . . s u b [ k ] = = s u b [ i − k − 1 ] . . . s u b [ i − 1 ] sub[0]...sub[k]==sub[i-k-1]...sub[i-1] sub[0]...sub[k]==sub[i−k−1]...sub[i−1]
上式等价于
n e x t [ i ] = k + 1 ; next[i]=k+1; next[i]=k+1;
  这太好了，我们如果有next[i-1]=k并且sub[k]=sub[i-1]就能立即退出next[i]的值。

  然后我们可以让i++,k++，去计算下一个next[]数组值；

  好，我们现在处理了sub[k]和sub[i-1]相等的情况，如果不相等呢

情况2 sub[k]!=sub[i-1]

  不相等的时候，我们想做的是再找一次符合条件的最大相等子串(除了上次以外的最大)，即找除上一次的两个最大相等子串外以的sub[0]为开头，以sub[i-2]为结尾的两个最大相等子串，然后再比较sub[i-1]和sub[k]。

  这里就体现了这个算法的巧妙之处了，我们把这个问题转化一下，

利用已知next[i-1]=k 有
s u b [ 0 ] . . . s u b [ k − 1 ] = = s u b [ i − k − 1 ] . . . s u b [ i − 2 ] sub[0]...sub[k-1]==sub[i-k-1]...sub[i-2] sub[0]...sub[k−1]==sub[i−k−1]...sub[i−2]
s u b [ i − 2 ] = s u b [ k − 1 ] sub[i-2]=sub[k-1] sub[i−2]=sub[k−1]

. .​ .​

s u b [ 0 ] = s u b [ i − k − 1 ] sub[0]=sub[i-k-1] sub[0]=sub[i−k−1]

  所以我们直接找以sub[0]为开头，以sub[k-1]为结尾的两个最大相等子串（也就是在前缀sub[0]…sub[k-1]中找最大相等子串）.

  这样做合理的，原因如下：

  首先上一次的最大相等子串的长度是k，我们要找长度比它小的最大相等子串，在前缀这样长度为k的串里头找出来的最大相等子串长度一定小于k;

  而且由于找的是更小的最大相等子串，以sub[k-1]结尾的子串要在sub[i-k-1]后面的位置找(中间(sub[k]…sub[i-k-2])部分是不用考虑的),并且这些位置的元素本来就和前缀(sub[0]…sub[k-1])中的元素是相等的，我们不会因为是在sub[0]…sub[k-1]中找而漏掉元素或者使得找到的最大相等子串不是除原最大相等子串以外最大的。

  我们可以用一副图来加深我们的理解。

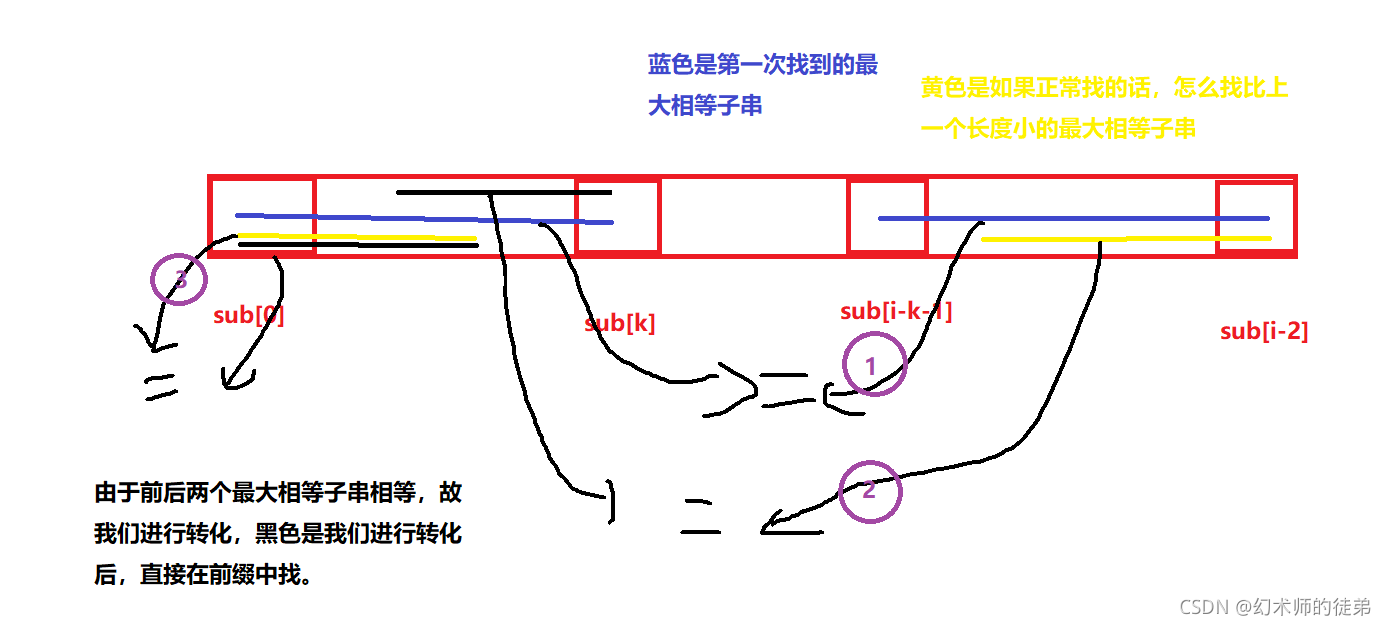
  我们再来回头看next数组元素值的意义，

  next[i-1]=k意味着以sub[0]为开头，以sub[i-2]为结尾的最大相等子串的长度是k，并且由于是以sub[0]开头的，这两个子串中以sub[0]开头的子串的结尾位置的下一个位置的下标就是k。

  所以找以sub[0]开头以sub[k]结尾的最大相等子串并把以sub[0]开头的子串的结尾位置的后一个位置赋给k就是k=next[k]。

  所以对情况2的操作就是k=next[k].

  接下来我们再次比较sub[i-1]和sub[k]，如果相等就回到了情况1,

  否则我们仍处于情况2，继续k=next[k]。

三、C语言实现

首先我们先实现KMP算法的总体框架

2.1 KMP函数

#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include <stdio.h>

int KMP(char* str, char* sub, int pos)
//pos表示从str串下标为pos的地方开始找
{
	assert(str && sub);//保证不是空指针
	int len1 = strlen(str);
	int len2 = strlen(sub);
	if (len1 == 0 || len2 == 0 || pos >= len1 || pos < 0)
	//保证不是空串且pos值合理
	{
		return -1;
	}
	int* next = (int*)malloc(len2 * sizeof(int));//用来存放next数组
	int i = pos;//用来遍历str串
	int j = 0;//用来遍历sub串
	Getnext(next, sub, len2);//求解next数组
	while (i < len1 && j< len2)
	//i还没有走出len1，j还没有走出len2，说明当还没遍历完
	{
		if (j==-1 || str[i] == sub[j])
		//如果字符相等就往下走
        //这里j==-1也可以进if语句原因见图1
		{
			i++;
			j++;
		}
		//如果不等，根据我们的思想j要调到next[j]的位置
		else
		{
			j = next[j];
		}
	}
	free(next);
	next = NULL;
	if (j >= len2)
	//如果j能遍历完子串，其坐标就是len2(到\0)
	{
		return i - j;//返回找到的子串的位置
	}
	else
	//长度不够len2的话还跳出了循环，都遍历完了也没找到
	{
		return -1;
	}
}

图1：

2.2 Getnext函数

void Getnext(int* next, char* sub, int num)
{
	next[0] = -1;
	next[1] = 0;
	int i = 2;//记录当前正在求解的next的下标
	//求next从2开始往后求到num-1
	int k = 0;
	//存储next[i-1]的值用来做判断
	while (i < num)
	{
		if ( k==-1 || sub[i - 1] == sub[k])
		//如果相等 推导出next[i]=k+1 并且把i往后拨一个去计算下一个next, 
        //k也往后拨一个,这样可以走到上一轮回溯位置的下一个位置，如果此位置的字符和sub[i-1]相等就可以继续计算next数组值
        //k==-1也进入if语句的解释见下图
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}

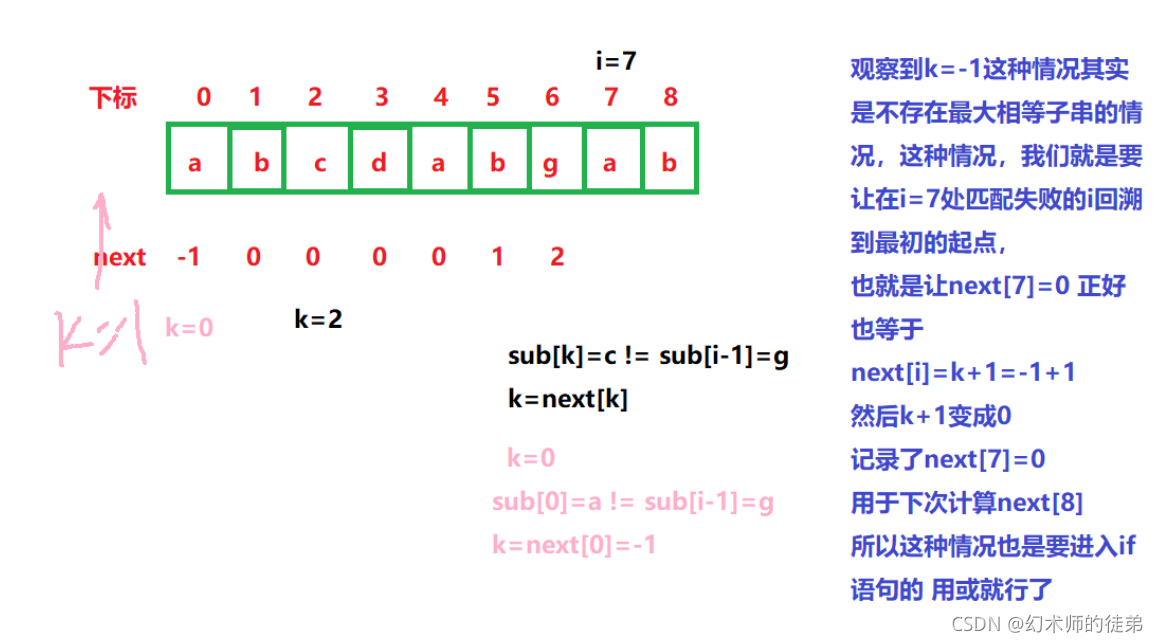
  这里有一种特殊情况，如果k=next[0]=-1，回溯到了-1去了怎么办，这样就不能访问sub[k]=sub[-1]了，属于越界访问。

同理 我们用一幅图来解释怎么处理这种情况

四、改进的KMP算法

  人们发现，KMP算法仍然有一定的缺陷，如图

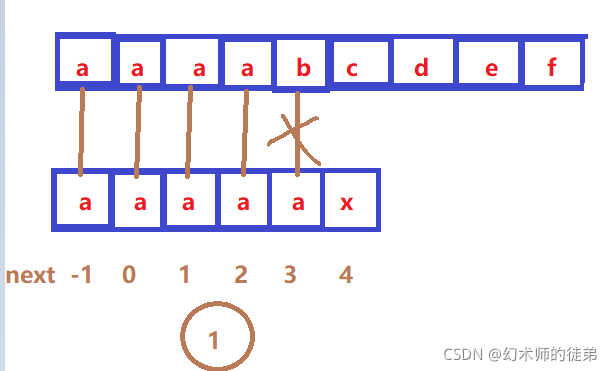
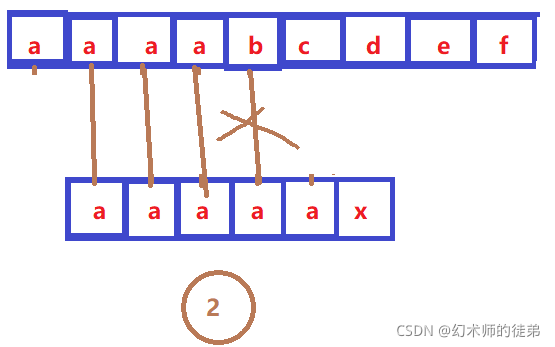
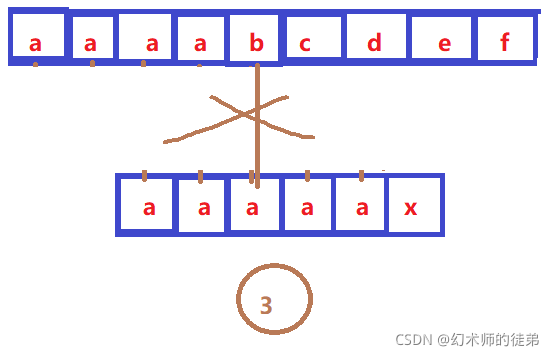
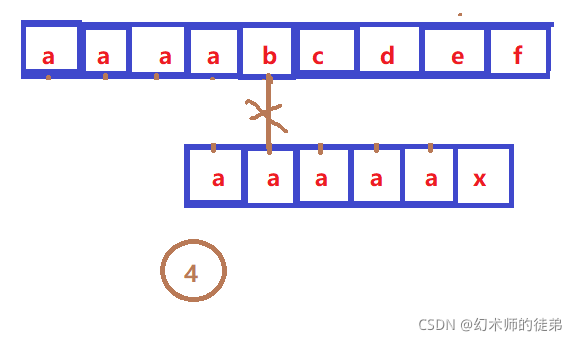
  ②③④⑤都是多余的判断，这是由于sub[0] sub[1] sub[2] sub[3] 都等于sub[4],而sub[4]不等于str[4],所以我们这些回退都是没有必要的，

  为此我们可以这样设计，考虑一个nextval数组，每次计算时，先让nextval[i]就存放next[i]的值，

然后对比sub[i]和sub[next[i]]这两个字符

• 如果相等的话，那说明它回溯到的位置的字符和它一样，我们让它的nextval[i]存放这个回溯到字符的nextval[nextval[i]]

• 如果不相等，nextval[i]就保留next[i]的值即可。

  这样的话，我们就保证了当原字符和它的回溯字符相等的时候，原字符的回溯位置会变成它回溯字符的回溯字符位置,避免了j一次一次无必要回退。

下图直观的讲解了计算nextval数组的动作:

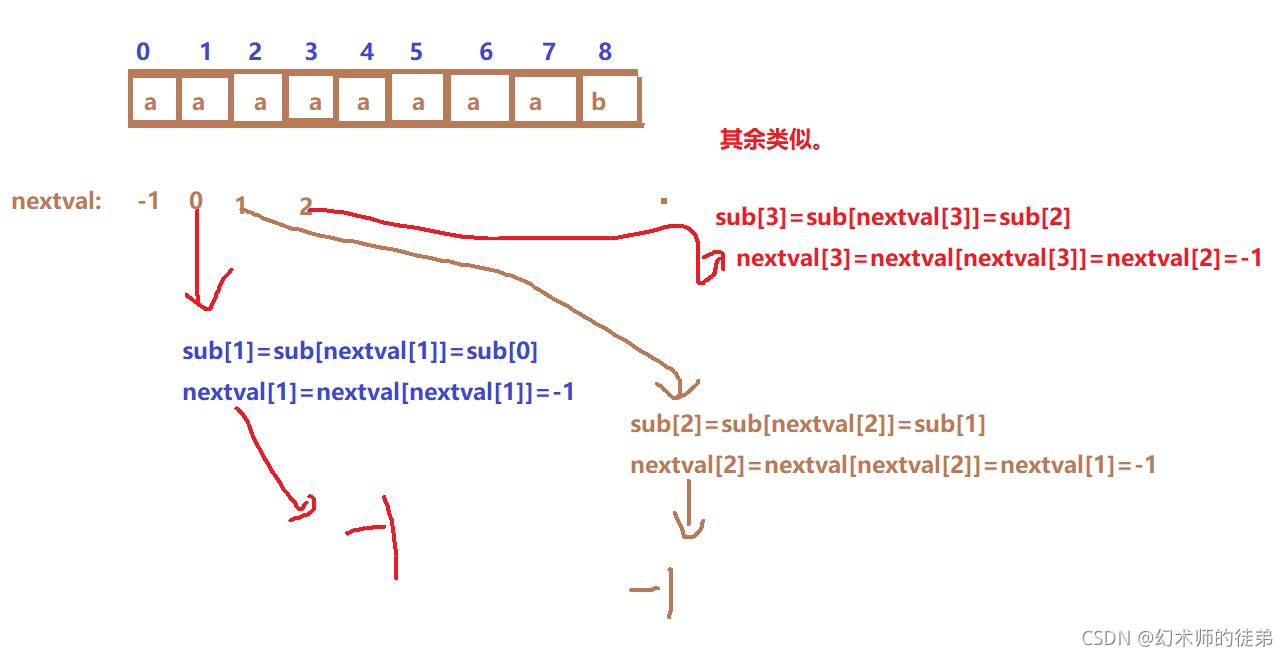
我们可以把这个想法用C语言实现如下

void Getnextval(int* nextval, char* sub, int num)
{
	nextval[0] = -1;
	nextval[1] = 0;
	int i = 1;//记录当前正在求解的next的下标
	//求next从1开始往后求到num-1
	int k = -1;
	//存储next[i-1]的值用来做判断
	while (i < num)
	{
		if (k == -1 || sub[i - 1] == sub[k])
		//如果相等 推导出next[i]=k+1 并且把i往后拨一个 k也往后拨一个
		{
			nextval[i] = k + 1;
			if (sub[k+1] == sub[i])
			{
				nextval[i] = nextval[nextval[i]];
			}
			i++;
			k++;
		}
		else
		{
			k = nextval[k];
		}
	}
}



int KMP(char* str, char* sub, int pos)
//pos表示从str串下标为pos的地方开始找
{
	assert(str && sub);//保证不是空指针
	int len1 = strlen(str);
	int len2 = strlen(sub);
	if (len1 == 0 || len2 == 0 || pos >= len1 || pos < 0)
	//保证不是空串且pos值合理
	{
		return -1;
	}
	int* next = (int*)malloc(len2 * sizeof(int));//用来存放next数组
	int i = pos;//用来遍历str串
	int j = 0;//用来遍历sub串
	Getnextval(next, sub, len2);//求解nextval数组
	while (i < len1 && j<len2 )
	//当还没遍历完
	{
		if (j==-1 || str[i] == sub[j])
		//如果字符相等就往下走
		{
			i++;
			j++;
		}
		//如果不等，根据我们的思想j要调到next[j]的位置
		else
		{
			j = next[j];
		}
		//我们知道有可能j一直往回回溯
		//回溯到了j=next[j]=0,
		//然后0位置还是不相等就回溯到了j=next[0]=-1的地方
	}
	free(next);
	next = NULL;
	if (j >= len2)
	//如果j能遍历完子串，其坐标就是len2(到\0)
	{
		return i - j;//返回找到的子串的位置
	}
	else
	//长度不够len2的话还跳出了循环，都遍历完了也没找到
	{
		return -1;
	}
}
int main()
{
	int ret = KMP("aaaaaaaaaaabbbbbbbbbbbbbbbbbbbaaaaaaaaaaa", "aaaaaaaabbbbbbbb", 0);
	printf("%d", ret);
	return 0;
}

参考文献：

1.《大话数据结构》 程杰 清华大学出版社