零基础使用 MATLAB 求解偏微分方程（建议收藏）

偏微分开源工具介绍

百分之九十以上的重要的工程和数学科学研究，和偏微分方程都脱不开关系。在所有的偏微分方程中，百分之九十九都是没有解析解的。没有解析解怎么办，我们只能通过有限元或者有限差分等方法，求解偏微分方程数值解。如果您有一些代码基础，建议参考我的几篇有限经典博文，简单问题可在此基础上进行修改。

有限元方法入门：有限元方法简单的一维算例
有限元方法入门：有限元方法简单的二维算例（三角形剖分）
有限元方法入门：有限元方法简单的二维算例（矩形剖分）

对于做工程的朋友，不会偏微分方程数值解，怎么办？没关系，我推荐一些求解各类偏微分方程的容易入门的开源的软件包和工具，它们是：

• Free FEM++（足够傻瓜又不失自由度，强烈建议做工程的朋友可以学习一下）
• FEniCS(C++/Python, 开始于芝加哥大学和查尔姆斯理工大学)
• PETSC (C/Python, 美国阿贡国家实验室)
• deal.II (C++, 开始于德国海德堡大学)
• MFEM (C++, 美国劳伦斯利弗莫尔国家实验室)
• PHG (C, 张林波, 中国科学院)
• AFEPACK (C++, 李若, 北京大学）
• FEALPy（Python，魏华祎，湘潭大学）
• IFEM (MATLAB, 陈龙, UCI)
• NGSolve（C++/Python，Christoph 等）
• PHOEBESolver（ Fortran and C/C++，宁夏大学，葛永斌）
  [1]: GCGE（C/MATLAB，中国科学院，谢和虎，特征值求解）
• ……

当然，商业有限元软件 ansys 等，也非常推荐学工程的朋友去学习，如果要深挖算法的，建议还是用开源的。

好，有的同学说，这些对你们来说还是太难了。没关系，我可以祭出大招：MATLAB PDE工具箱。为什么它比上面的简单呢？主要是因为，它有可视化的 GUI 工具，你实在不会写代码，你用鼠标点点，也能 “写” 出像模像样的代码。

PDE 工具箱函数汇总介绍

PDE 工具箱包含比较多的工具，典型的几个函数如下所示。

% 偏微分方程工具箱
%
% 使用结构化的工作流定义和求解 PDEs
%   createpde               - 创建 PDE 分析模型
%   geometryFromEdges       - 从 DECSG or PDEGEOM 创建 2D 几何图形
%   importGeometry          - 从 STL 文件创建 3D 几何图形
%   geometryFromMesh        - 从三角网格创建几何图形
%   multicuboid             - 组合立方体胞单元创建 3D 几何图形
%   multicylinder           - 组合若干柱状胞单元创建 3D 几何图形
%   multisphere             - 组合若干球单元创建 3D 几何图形
%   addVertex               - 在几何区域边界上添加一个顶点
%   specifyCoefficients     - 指定区域和或者子区域的 PDE 系数
%   applyBoundaryCondition  - 给几何区域施加边界条件
%   setInitialConditions    - 设定 PDE 初始条件
%   generateMesh            - 从几何生成一个网格
%   solvepde                - 求解 PDE
%   solvepdeeig             - 求解 PDE 特征值问题
%   assembleFEMatrices      - 组装中间的有限元矩阵
%   createPDEResults        - 创建一个用于后处理的结果对象
%   pdegplot                - 绘制 PDE 几何表示
%   pdemesh                 - 绘制 PDE 网格
%   pdeplot                 - 绘制二维 PDE 网格和结果
%   pdeplot3D               - 绘制 3D PDE 网格和结果
%   interpolateSolution     - 在指定的空间位置插入解
%   evaluateGradient        - 在指定的空间位置评估解的梯度
%   evaluateCGradient       - 评估 PDE 解的通量
% 
% 使用热模型解决以传导为主的传热问题
%   thermalProperties       - 为热模型指定材料的热属性
%   internalHeatSource      - 指定热模型的内部热源
%   thermalBC               - 指定热模型的边界条件
%   thermalIC               - 设置热模型的初始条件或初始猜测
%   solve                   - 求解热模型中指定的传热问题
%   interpolateTemperature	- 在任意空间位置的热结果中插入温度
%   evaluateTemperatureGradient - 评估热解在任意空间位置的温度梯度
%   evaluateHeatFlux        - 在节点或任意空间位置评估热解的热通量
%   evaluateHeatRate        - 评估垂直于指定边界的综合热流率
% 
% 使用结构模型解决静态、模态和瞬态线性弹性问题
%   structuralProperties    - 为模型分配结构材料属性
%   structuralBodyLoad      - 将体载荷应用于结构模型
%   structuralBoundaryLoad  - 在几何边界上施加结构载荷
%   structuralBC            - 将边界条件应用于结构模型
%   structuralIC            - 设置初始位移和速度
%   structuralDamping       - 为结构模型指定比例阻尼参数
%   solve                   - 求解 StructuralModel 中指定的结构模型
%   evaluateStress          - 评估节点位置的应力
%   evaluateStrain          - E评估节点位置的应变
%   evaluateVonMisesStress  - 评估节点位置的 von Mises 应力
%   evaluatePrincipalStrain - 计算节点位置的主要应变
%   evaluatePrincipalStress - 计算节点位置的主应力
%   evaluateReaction        - 评估边界上的反作用力
%   interpolateDisplacement - 在指定的空间位置插入位移
%   interpolateVelocity     - 在指定的空间位置插入速度
%   interpolateAcceleration - 在指定的空间位置插入加速度
%   interpolateStress       - 在指定的空间位置插入应力
%   interpolateStrain       - 在指定的空间位置插入应变
%   interpolateVonMisesStress - 在指定空间位置内插 von Mises 应力
%
% 使用非结构化工作流程求解 PDE
%   adaptmesh   - 自适应网格生成和 PDE 解
%   assema      - 组装面积积分贡献
%   assemb      - 组装边界条件贡献
%   assempde    - 组装 PDE 问题
%   hyperbolic  - 解决双曲线问题
%   parabolic   - 解决抛物线问题
%   pdeeig      - 解决特征值 PDE 问题
%   pdenonlin   - 解决非​​线性 PDE 问题
%   poisolv     - 矩形网格上泊松方程的快速解
%
% 用户界面算法和实用程序
%   pdecirc     - 画圆
%   pdeellip    - 绘制椭圆
%   pdemdlcv    - 转换 MATLAB 4.2c 模型 MATLAB 文件以与 MATLAB 5 一起使用
%   pdepoly     - 绘制多边形
%   pderect     - 绘制矩形.
%   pdeModeler  - PDE Modeler 图形用户界面 (GUI)
%
% 几何算法
%   csgchk      - 检查几何描述矩阵的有效性
%   csgdel      - 删除最小区域之间的边界
%   decsg       - 将构造实体几何分解为最小区域
%   initmesh    - 构建初始三角形网格
%   jigglemesh  - 抖动三角形网格的内部点
%   pdearcl     - 参数化表示和弧长之间的插值
%   poimesh     - 在矩形几何体上制作规则网格
%   refinemesh  - 细化三角形网格
%   wbound      - 写入边界条件规范数据文件
%   wgeom       - W写入几何规格数据文件
%
% 绘图函数
%   pdecont     - 等高线图的速记命令
%   pdegplot    - 绘制 PDE 几何
%   pdemesh     - 绘制 PDE 三角形网格
%   pdeplot     - 通用 PDE 工具箱绘图函数
%   pdesurf     - 曲面图的速记命令
%
% 实用算法
%   dst         - 离散正弦变换
%   idst        - 逆离散正弦变换
%   pdeadgsc    - 使用相对容差标准挑选坏三角形
%   pdeadworst  - 选择相对于最差值的坏三角形
%   pdecgrad    - 计算 PDE 解的通量
%   pdeent      - 与给定三角形集相邻的三角形的索引
%   pdegrad     - 计算 PDE 解的梯度
%   pdeintrp    - 将函数值插入到三角形中点
%   pdejmps     - 适应的误差估计
%   pdeprtni    - 将函数值内插到网格节点
%   pdesde      - 与一组子域相邻的边的索引
%   pdesdp      - 一组子域中的点索引
%   pdesdt      - 一组子域中的三角形索引
%   pdesmech    - 计算结构力学张量函数
%   pdetrg      - 三角形几何数据
%   pdetriq     - 测量网格三角形的质量
%   poiasma     - 泊松方程的边界点矩阵贡献
%   poicalc     - 矩形网格上泊松方程的快速解
%   poiindex    - 矩形网格的规范排序点的索引
%   sptarn      - 求解决广义稀疏特征值问题
%   tri2grid    - 从 PDE 三角形网格插值到矩形网格
%
% 用户定义的算法
%   pdebound    - 边界 MATLAB 文件
%   pdegeom     - 几何 MATLAB 文件
% 
% 对象创建函数。这些函数不是直接调用的。
%   PDEModel          - 表示 PDE 模型的容器
%   GeometricModel    - 模型边界的几何表示
%   AnalyticGeometry  - 来自 PDEGEOM 或 DECSG 几何矩阵的 2D 几何对象
%   DiscreteGeometry  - 分面边界的几何表示
%   BoundaryCondition - 定义 PDE 的边界条件
%   CoefficientAssignmentRecords  - 方程系数的分配
%   CoefficientAssignment         - 指定区域或子域上的所有 PDE 系数
%   InitialConditionsRecords   - 记录初始条件的分配
%   GeometricInitialConditions - 区域或区域边界上的初始条件
%   NodalInitialConditions  - 在网格节点指定的初始条件
%   PDEResults           - PDE 解及其派生量
%   StationaryResults    - PDE 解及其派生量
%   TimeDependentResults - PDE 解及其派生量
%   EigenResults         - PDE 解表示
%   StructuralModel      - 表示结构分析模型的容器
%   ThermalModel         - 表示热分析模型的容器
%   ThermalMaterialAssignment - 指定区域或子区域的材料属性
%   HeatSourceAssignment - 指定域或子域上的热源
%   ThermalBC            - 定义热模型的边界条件 (BC)
%   GeometricThermalICs  - 区域或区域边界上的初始温度
%   NodalThermalICs      - 在网格节点指定的初始温度
%   ThermalResults       - 热解及其派生量
%   SteadyStateThermalResults - 稳态热模型解及其派生量
%   TransientThermalResults   - 瞬态热模型解及其派生量
%   StructuralMaterialAssignment - 区域或子域上的结构材料属性分配
%   BodyLoadAssignment   - 结构分析模型的体载荷分配
%   StructuralBC         - 定义结构模型的边界载荷或边界条件 (BC)
%   StructuralResults    - 结构解及其派生量
%   StaticStructuralResults - 静态结构模型解及其派生量
%   StructuralDampingAssignment - 结构分析模型的阻尼分配
%   GeometricStructuralICs - 区域上的初始位移和速度
%   NodalStructuralICs - 在网格节点指定的初始位移和速度
%   ModalStructuralResults - 结构模态分析结果
%   TransientStructuralResults - 瞬态结构模型解及其派生量
%

% 未记录的类和函数
%   pdeCalcFullU
%   pdeODEInfo
%   pdeParabolicInfo
%   pdeHyperbolicInfo

0 基础：GUI 界面操作

示例问题

没有什么编程基础，但是又想快速写出有限元程序的同学，建议使用图形界面进行编程，然后导出代码。做个简单的示例操作。比如要求解：
− Δ u = λ u u ∣ ∂ Ω = 0 Ω 是 一 个 L 型 区 域 ， 如 下 图 所 示 -\Delta u = \lambda u\\ u|_{\partial \Omega}=0\\ \Omega 是一个L 型区域，如下图所示 −Δu=λuu∣∂Ω​=0Ω是一个L型区域，如下图所示

工具箱求解

• 打开 MATLAB
• 命令行窗口口输入 pdetool 回车
• 依次点击菜单栏如下按钮，其中点击 PDE 的时候，改成特征值模式
  

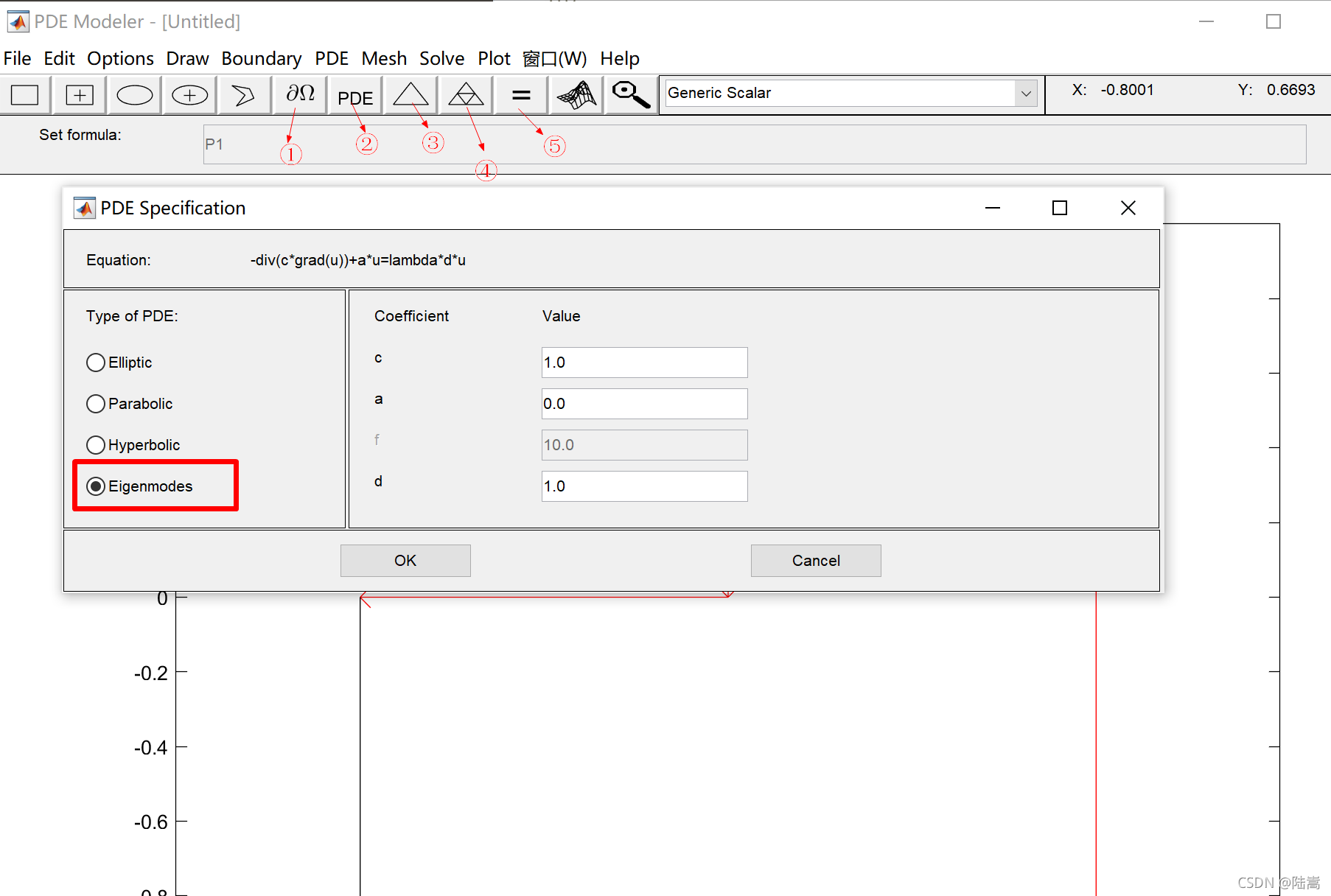
基础通过 GUI 界面生成的代码此由 pdetool 编写和读取，不应编辑。 有两个推荐的替代方案：

• 从 pdetool 导出所需的变量并创建一个 MATLAB 脚本，对这些变量执行操作。
• 使用 MATLAB 脚本完全定义问题。

导出为代码形式

得到求解结果后，保存为 main.m 文件，并打开。

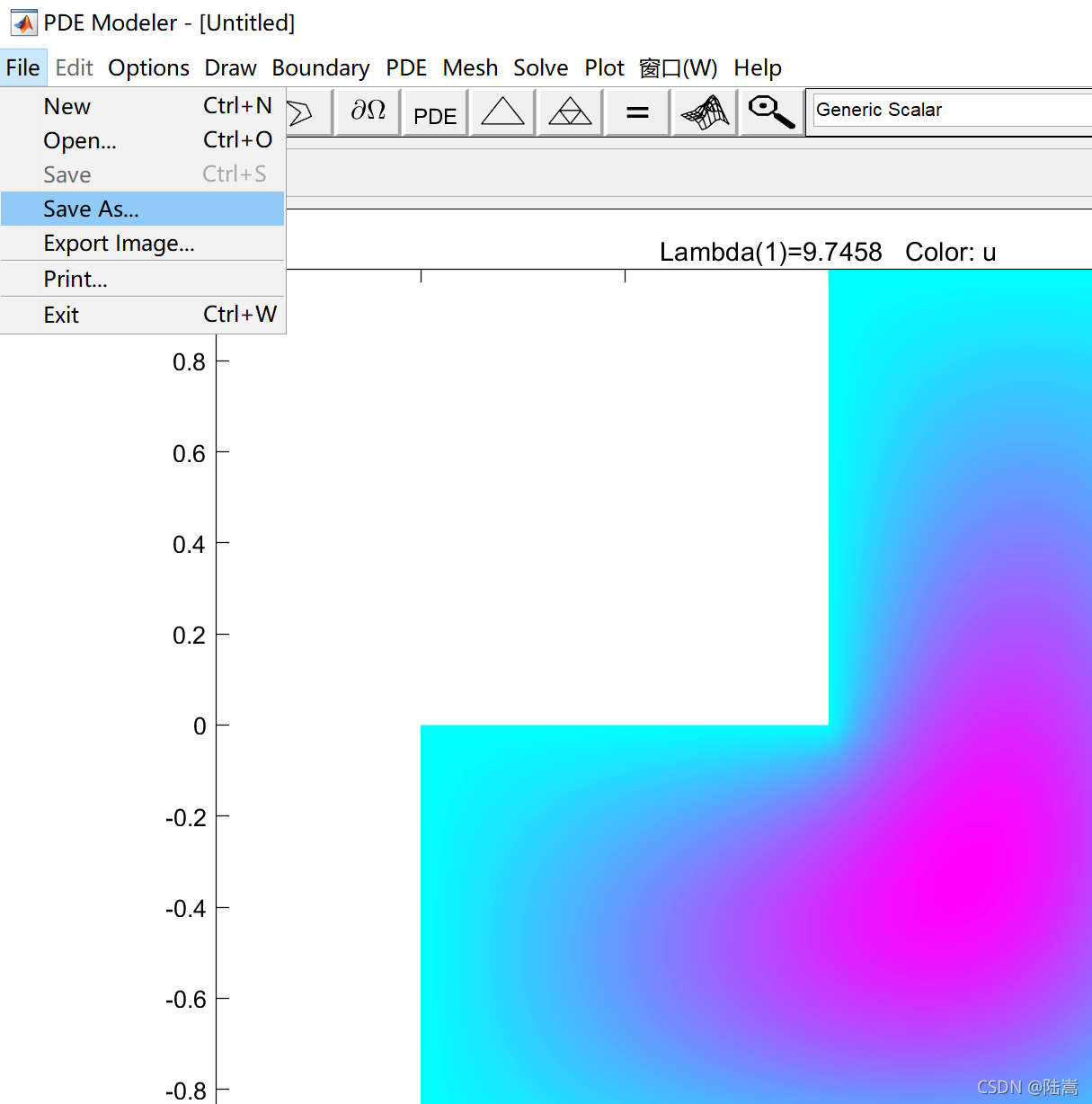
function pdemodel
[pde_fig,ax]=pdeinit;
pdetool('appl_cb',1);
set(ax,'DataAspectRatio',[1.5 1 1]);
set(ax,'PlotBoxAspectRatio',[1 0.74375917767988253 0.74375917767988253]);
set(ax,'XLim',[-1.5 1.5]);
set(ax,'YLim',[-1 1]);
set(ax,'XTickMode','auto');
set(ax,'YTickMode','auto');

% Geometry description:
pdepoly([ -1,...
 1,...
 1,...
 0,...
 0,...
 -1,...
],...
[ -1,...
 -1,...
 1,...
 1,...
 0,...
 0,...
],...
 'P1');
set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','P1')

% Boundary conditions:
pdetool('changemode',0)
pdesetbd(6,...
'dir',...
1,...
'1',...
'0')
pdesetbd(5,...
'dir',...
1,...
'1',...
'0')
pdesetbd(4,...
'dir',...
1,...
'1',...
'0')
pdesetbd(3,...
'dir',...
1,...
'1',...
'0')
pdesetbd(2,...
'dir',...
1,...
'1',...
'0')
pdesetbd(1,...
'dir',...
1,...
'1',...
'0')

% Mesh generation:
setappdata(pde_fig,'Hgrad',1.3);
setappdata(pde_fig,'refinemethod','regular');
setappdata(pde_fig,'jiggle',char('on','mean',''));
setappdata(pde_fig,'MesherVersion','preR2013a');
pdetool('initmesh')
pdetool('refine')

% PDE coefficients:
pdeseteq(4,...
'1.0',...
'0.0',...
'10.0',...
'1.0',...
'0:10',...
'0.0',...
'0.0',...
'[0 100]')
setappdata(pde_fig,'currparam',...
['1.0 ';...
'0.0 ';...
'10.0';...
'1.0 '])

% Solve parameters:
setappdata(pde_fig,'solveparam',...
char('0','1548','10','pdeadworst',...
'0.5','longest','0','1E-4','','fixed','Inf'))

% Plotflags and user data strings:
setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 0 1]);
setappdata(pde_fig,'colstring','');
setappdata(pde_fig,'arrowstring','');
setappdata(pde_fig,'deformstring','');
setappdata(pde_fig,'heightstring','');

% Solve PDE:
pdetool('solve') 

代码导出相关数据

当前目录下，保存如下代码为 matqueque。

function y = matqueue(p0,p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18)
%MATQUEUE Creates and manipulates a figure-based matrix queue.
%   FIG = MATQUEUE('create');
%   Create a queue figure and return its number.
%
%   FIG = MATQUEUE('find');
%   Searches the root window's children to find the queue
%   figure.  Returns 0 if no queue exists.
%
%   MATQUEUE('put', X1, X2, ..., X18);
%   Insert up to 18 matrices into the queue.  Create the
%   queue if none exists.
%   
%   X = MATQUEUE('get');
%   Get a matrix out the queue.  Return [] if the queue is
%   empty.
%
%   NUM_ITEMS = MATQUEUE('length');
%   Return the number of matrices in the queue.  Return -1 if
%   no buffer exists. 
%
%   MATQUEUE('clear')
%   Empty the queue.
%
%   MATQUEUE('close')
%   Close the queue figure.


buffer_name = 'FIFO Buffer';

if (nargin < 1)
  action = 'create';
else
  action = lower(p0);
end

if (strcmp(action, 'create'))
  
  %==================================================================
  % Create a new queue.
  %
  % matqueue('create');
  %==================================================================

  narginchk(1,1);
  nargoutchk(0,1);
  
  oldFig = findobj(allchild(0), 'flat', 'Visible', 'on');

  buffer_fig = matqueue('find');
  if (buffer_fig ~= 0) 
    % Buffer already exists; do nothing
    return;
  end

  buffer_fig = figure('Name', buffer_name, ...
      'Visible', 'off',...
      'HandleVisibility', 'callback', ...
      'IntegerHandle', 'off', ...
      'NumberTitle', 'off', ...
      'Tag', buffer_name);
  if (~isempty(oldFig))
    figure(oldFig(1));
  end
  
  queue_holder = uicontrol(buffer_fig, 'Style', 'text', ...
      'Visible', 'off', 'Tag', 'QueueHolder');

  y = buffer_fig;

  return;
  
elseif (strcmp(action, 'find'))
  
  %==================================================================
  % Find the queue figure.  If no queue figure exists, return 0.
  %
  % matqueue('find');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);
  
  % Search the root's children for a figure with the right name
  buffer_number = findobj(allchild(0), 'flat', 'Tag', buffer_name);
  if (isempty(buffer_number))
    y = 0;
  else
    y = buffer_number(1);
  end
  
  return;
  
elseif (strcmp(action, 'put'))
  
  %==================================================================
  % Put matrices into the queue.  Queue figure is created if none
  % exists.
  %
  % matqueue('put', X1, X2, ..., X18);
  %==================================================================
  
  narginchk(2,19);
  nargoutchk(0,0);
  
  buffer_fig = matqueue('find');
  if (buffer_fig == 0)
    buffer_fig = matqueue('create');
  end
  
  queue_holder = findobj(get(buffer_fig, 'Children'), 'flat', 'Tag', 'QueueHolder');
  if (isempty(queue_holder))
    error(message('pde:matqueue:corruptMatrixQueue'));
  end
  
  handles = get(queue_holder, 'UserData');
  
  num_inputs = nargin-1;
  new_handles = zeros(1, num_inputs);
  for i = 1:num_inputs
    arg_name = ['p', num2str(i)];
    try_string = ['new_handles(num_inputs+1-i)=uicontrol(buffer_fig,', ...
        ' ''Style'',''text'',''Visible'','...
        ' ''off'',''UserData'',', arg_name, ');'];
    eval(try_string);
  end
  
  set(queue_holder, 'UserData', [new_handles handles]);
  
  return;
  
elseif (strcmp(action, 'get'))
  
  %==================================================================
  % Return earliest matrix item in the queue.  Errors out if there's
  % no queue.  Returns empty matrix if queue is empty.
  %
  % X = matqueue('get');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);

  buffer_fig = matqueue('find');
  if (buffer_fig == 0)
    % No buffer; return empty matrix.
    y = [];
    return;
  end

  queue_holder = findobj(get(buffer_fig, 'Children'), 'flat', 'Tag', 'QueueHolder');
  if (isempty(queue_holder))
    error(message('pde:matqueue:corruptMatrixQueue'));
  end
  
  handles = get(queue_holder, 'UserData');
  N = length(handles);
  if (N > 0)
    y = get(handles(N), 'UserData');
    delete(handles(N));
    handles(N) = [];
    set(queue_holder, 'UserData', handles);
  else
    % Nothing in the buffer; return empty matrix
    y = [];
  end
  
  return;
  
elseif (strcmp(action, 'length'))
  
  %==================================================================
  % Returns the length of the queue.  Returns -1 if no queue 
  % figure exists.
  %
  % num_items = matqueue('length');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);
  
  buffer_fig = matqueue('find');
  if (buffer_fig == 0)
    % No buffer!  Return 0.
    y = 0;
    return;
  end
  
  queue_holder = findobj(get(buffer_fig, 'Children'), 'flat', 'Tag', 'QueueHolder');
  if (isempty(queue_holder))
    error(message('pde:matqueue:corruptMatrixQueue'));
  end
  
  y = length(get(queue_holder, 'UserData'));
  
  return;

elseif (strcmp(action, 'clear'))
  
  %==================================================================
  % Clear the queue.
  %
  % matqueue('clear');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);
  
  buffer_fig = matqueue('find');
  if (buffer_fig == 0)
    % No buffer; nothing to do.
    return;
  end
  
  queue_holder = findobj(get(buffer_fig, 'Children'), 'flat', 'Tag', 'QueueHolder');
  if (~isempty(queue_holder))
    delete(queue_holder);
  end
  
  queue_holder = uicontrol(buffer_fig, 'Style', 'text', ...
      'Visible', 'off', 'Tag', 'QueueHolder');
  
  return;
  
elseif (strcmp(action, 'close'))
  
  %==================================================================
  % Close the queue figure.
  %
  % matqueue('close');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);
  
  buffer_fig = matqueue('find');
  if (buffer_fig ~= 0)
    close(buffer_fig);
  end
  
  return;
  
else
  
  error(message('pde:matqueue:unknownAction'));
  
end

同样地，将如下代码存为 matqdlg。

function y = matqdlg(P0,P1,V1,P2,V2,P3,V3,P4,V4,P5,V5,P6,V6,P7,V7,P8,V8,P9,V9)
%MATQDLG Workspace transfer dialog box.
%   MATQDLG('ws2buffer', {prop/value pairs})
%   Put up a dialog box that invites the user to enter a comma-separated
%   list of expressions.  When user clicks OK,  eval the expressions 
%   one at a time, putting the results into the buffer.  Allowable
%   properties include 'PromptString', which may be a string matrix,
%   'OKCallback', which will be eval'ed when the user finishes
%   with the dialog box by typing <Return> in the entry field or 
%   clicking OK, 'CancelCallback', which will be eval'ed when the user 
%   clicks Cancel, and 'EntryString', the default user entry.  
%   Figure properties are also allowed in this list, such as 'Name'.
%
%   MATQDLG('buffer2ws', {prop/value pairs})
%   Put up a dialog box that invites the user to enter N comma-separated
%   variable names, where N is the number of items in the buffer.  Get
%   items out of the buffer one at a time, storing the results in
%   indicated workspace variables.  Allowable properties include 
%   'PromptString', 'OKCallback', 'CancelCallback', and 'EntryString'.
%   These work the same way as in the 'ws2buffer' action.
%
%   Y = MATQDLG('get_entry');
%   Return the user-entered string in the entry field of the workspace
%   transfer dialog box.
%
%   H = MATQDLG('find')
%   Return the handle of the dialog box figure.
%
%   H = MATQDLG('create')
%   Create the dialog box figure, returning its handle.

% MATLAB-files required:  matqparse.m, ws2matq.m, matq2ws.m.

buffer_tag = 'Workspace Transfer';
buffer_name = '';

if (nargin < 1)
  action = 'create';
else
  action = lower(P0);
end

if (strcmp(action, 'create'))
  
  %==================================================================
  % Create a new queue.
  %
  % matqdlg('create');
  %==================================================================

  narginchk(1,1);
  nargoutchk(0,1);
  
  buffer_fig = matqdlg('find');
  if (buffer_fig ~= 0) 
    % Queue already exists; do nothing
    return;
  end
  
  screenSize = get(0,'ScreenSize');
  width = 415;
  height = 136;
  left = (screenSize(3) - width) / 2;
  bottom = (screenSize(4) - height) / 2;

  buffer_fig = figure('Name', buffer_name, 'Visible', 'off',...
      'HandleVisibility', 'callback', ...
      'IntegerHandle', 'off', ...
      'Units', 'pixels', ...
      'Position', [left bottom width height], ...
      'Colormap', [], ...
      'MenuBar', 'none', ...
      'Color', get(0, 'DefaultUIControlBackgroundColor'), ...
      'DefaultUIControlInterruptible','on', ...
      'Tag', buffer_tag, ...
      'NumberTitle', 'off');
  
  axes('Visible', 'off', 'Parent', buffer_fig);
  
  ok = uicontrol(buffer_fig, ...
      'Style', 'push', ...
      'Units', 'normalized', ...
      'Position', [.63 .06 .15 .24], ...
      'Tag', 'OK', ...
      'String', 'OK');
  
  cancel = uicontrol(buffer_fig, ...
      'Style', 'push', ...
      'Units', 'normalized', ...
      'Position', [.80 .06 .15 .24], ...
      'Tag', 'Cancel', ...
      'String', 'Cancel');
  
  prompt = uicontrol(buffer_fig, ...
      'Style', 'text', ...
      'Units', 'normalized', ...
      'Position', [.05 .76 .90 .15], ...
      'String', '', ...
      'Min', 1, ...
      'Max', 3, ...
      'Tag', 'Prompt', ...
      'Horizontal', 'left');

  entry = uicontrol(buffer_fig, ...
      'Style', 'edit', ...
      'Units', 'normalized', ...
      'Position', [.05 .46 .90 .31], ...
      'BackgroundColor', 'w', ...
      'ForegroundColor', 'k', ...
      'Tag', 'Entry', ...
      'Horizontal', 'left');
  
  y = buffer_fig;

  return;
  
elseif (strcmp(action, 'find'))
  
  %==================================================================
  % Find the queue figure.  If no queue figure exists, return 0.
  %
  % matqdlg('find');
  %==================================================================
  
  narginchk(1,1);
  nargoutchk(0,1);
  
  % Search the root's children for a figure with the right tag
  buffer_number = findobj(allchild(0), 'flat', 'Type', 'figure', ...
      'Tag', buffer_tag);
  if (isempty(buffer_number))
    y = 0;
  else
    y = buffer_number(1);
  end
  
  return;
  
elseif (strcmp(action, 'ws2buffer'))
  
  %==================================================================
  % Invoke the dialog box in workspace-to-buffer mode.
  %
  % matqdlg('ws2buffer')
  %==================================================================
  
  narginchk(1,19);
  if (rem(nargin,2) ~= 1)
    error(message('pde:matqdl:invalidNumberOfArgs'));
  end

  % Remember the current visible figure.
  figHandles = findobj(allchild(0), 'flat', 'Visible', 'on');
  
  % Set up default properties.
  ok_string = '';
  cancel_string = '';
  entry_string = '';
  prompt_string = 'Enter workspace variable names or expressions:';
  
  buffer_fig = matqdlg('find');
  if (buffer_fig == 0)
    buffer_fig = matqdlg('create');
  end
  if (~isempty(figHandles))
    set(buffer_fig, 'UserData', figHandles(1));
  end
  
  % Process param/value pairs.
  num_properties = (nargin - 1)/2;
  for k = 1:num_properties
    prop_arg_name = ['P' num2str(k)];
    val_arg_name = ['V' num2str(k)];
    prop_arg = lower(eval(prop_arg_name));
    val_arg = eval(val_arg_name);
    if (strcmp(prop_arg, 'promptstring'))
      prompt_string = val_arg;
    elseif (strcmp(prop_arg, 'okcallback'))
      ok_string = val_arg;
    elseif (strcmp(prop_arg, 'cancelcallback'))
      cancel_string = val_arg;
    elseif (strcmp(prop_arg, 'entrystring'))
      entry_string = val_arg;
    else
      set(buffer_fig, prop_arg, val_arg);
    end
  end
  
  promptButton = findobj(buffer_fig, 'Tag', 'Prompt');
  entry = findobj(buffer_fig, 'Tag', 'Entry');
  okButton = findobj(buffer_fig, 'Tag', 'OK');
  cancelButton = findobj(buffer_fig, 'Tag', 'Cancel');
  set(okButton, 'UserData', ok_string, 'Callback', {@okButtonCallback,'ws'});
  set(cancelButton, 'UserData', cancel_string, 'Callback', @cancelButtonCallback);
  set(promptButton, 'String', prompt_string);
  set(entry, 'String', entry_string);
  
  % Adjust height of figure and prompt box.
  prompt_lines = size(prompt_string,1);
  if (prompt_lines > 1)
    set([promptButton entry okButton cancelButton], 'Units', 'pixels');
    prompt_position = get(promptButton, 'Position');
    prompt_height = prompt_position(4);
    increase = (prompt_lines-1) * prompt_height;
    fig_position = get(buffer_fig, 'Position');
    set(promptButton, 'Position', prompt_position + [0 0 0 increase]);
    set(buffer_fig, 'Position', fig_position + [0 0 0 increase]);
    set([promptButton entry okButton cancelButton], 'Units', 'normalized');
  end

  drawnow;
  figure(buffer_fig);
  
  return

elseif (strcmp(action, 'buffer2ws'))
  
  %==================================================================
  % Invoke the dialog box in workspace-to-buffer mode.
  %
  % matqdlg('ws2buffer')
  %==================================================================
  
  narginchk(1,19);
  if (rem(nargin,2) ~= 1)
    error(message('pde:matqdl:invalidNumberOfArgs'));
  end
  
  % Remember the current visible figure.
  figHandles = findobj(allchild(0), 'flat', 'Visible', 'on');
  
  num_items = matqueue('length');
  if (num_items == 0)
    % If the queue is empty, there's nothing to do!
    error(message('pde:matqdl:emptyQueue'));
  end
  
  buffer_fig = matqdlg('find');
  if (buffer_fig == 0)
    buffer_fig = matqdlg('create');
  end
  if (~isempty(figHandles))
    set(buffer_fig, 'UserData', figHandles(1));
  end
  
  % Set up default properties.
  ok_string = '';
  entry_string = '';
  cancel_string = '';
  if (num_items == 1)
    prompt_string = 'Enter a variable name:';
  else
    prompt_string = sprintf('Enter %d variable names:', num_items);
  end
  
  % Process param/value pairs.
  num_properties = (nargin - 1)/2;
  for k = 1:num_properties
    prop_arg_name = ['P' num2str(k)];
    val_arg_name = ['V' num2str(k)];
    prop_arg = lower(eval(prop_arg_name));
    val_arg = eval(val_arg_name);
    if (strcmp(prop_arg, 'promptstring'))
      prompt_string = val_arg;
    elseif (strcmp(prop_arg, 'okcallback'))
      ok_string = val_arg;
    elseif (strcmp(prop_arg, 'cancelcallback'))
      cancel_string = val_arg;
    elseif (strcmp(prop_arg, 'entrystring'))
      entry_string = val_arg;
    else
      set(buffer_fig, prop_arg, val_arg);
    end
  end
  
  promptButton = findobj(buffer_fig, 'Tag', 'Prompt');
  set(findobj(buffer_fig, 'Tag', 'OK'), 'UserData', ok_string, ...
      'Callback', {@okButtonCallback,'mat'});
  set(findobj(buffer_fig, 'Tag', 'Cancel'), 'UserData', cancel_string, ...
      'Callback', @cancelButtonCallback);
  set(promptButton, 'String', prompt_string);
  set(findobj(buffer_fig, 'Tag', 'Entry'), 'String', entry_string);

  % Adjust height of figure and prompt box.
  prompt_lines = size(prompt_string,1);
  if (prompt_lines > 1)
    set([promptButton entry okButton cancelButton], 'Units', 'pixels');
    prompt_position = get(promptButton, 'Position');
    prompt_height = prompt_position(4);
    increase = (prompt_lines-1) * prompt_height;
    fig_position = get(buffer_fig, 'Position');
    set(promptButton, 'Position', prompt_position + [0 0 0 increase]);
    set(buffer_fig, 'Position', fig_position + [0 0 0 increase]);
    set([promptButton entry okButton cancelButton], 'Units', 'normalized');
  end

  drawnow;
  figure(buffer_fig);
  
  return;
  

elseif (strcmp(action, 'get_entry'))
  
  %==================================================================
  % Get the user-entered string in the entry field.
  %
  % string = matqdlg('get_entry');
  %==================================================================
  
  buffer_fig = matqdlg('find');
  if (buffer_fig < 1)
    y = [];
    return;
  end
  
  y = get(findobj(buffer_fig, 'Tag', 'Entry'), 'String');

  return;

else
  
  error(message('pde:matqdl:invalidAction'));
  
end

%--------------------------------------------
function   okButtonCallback(obj,evd,wsormat)

switch(wsormat)
 case 'ws'
  ws2matq
  
 case 'mat'
  matq2ws
  
 otherwise
  error(message('pde:matqdl:okButtonCallback:unknownOption'));

end
%-------------------------------------------

function cancelButtonCallback(obj,evd)

matqueue('clear');
eval(get(findobj(gcbf,'Tag','Cancel'),'UserData'));
close(matqdlg('find'));

将如下代码存为文件 matq2ws 。

%MATQ2WS Helper script for matqdlg.
%  MATQ2WS gets the user-entered comma-delimited string,
%  parses it, and then tries to put the queue contents one
%  at a time into the resulting variable names.  For
%  recoverable errors, the prompt is reset and the user can
%  try again.  Recoverable errors include empty input
%  string, string containing "#", too few variable names,
%  and too many variable names.  If the user types something
%  that cannot be a workspace variable name, that's a
%  nonrecoverable error.  The queue is cleared and made
%  invisible, and an error message is printed to the command
%  window. 

% Variable names (these need to be cleared before returning):
% var_string_ err_string_ new_prompt_ pound_ N_
% fatal_error_flag_ i_ expr_ try_string_ catch_string_ error_message_ 


var_string_ = get(findobj(gcbf,'Tag','Entry'), 'String');
[var_string_, err_string_] = matqparse(var_string_);
if (~isempty(err_string_))
  errordlg(char('Could not parse your expression.', err_string_), ...
      'Workspace Transfer Error', 'on');
  clear var_string_ err_string_ new_prompt_ ...
      pound_ N_ fatal_error_flag_ i_ expr_ try_string_ catch_string_ ...
      error_message_
  return;
end
N_ = size(var_string_, 1);
if (N_ < matqueue('length'))
  errordlg(char('You did not enter enough variable names.', ...
      'Please try again.'), 'Workspace Transfer Error', 'on');
  clear var_string_ err_string_ new_prompt_ ...
      pound_ N_ fatal_error_flag_ i_ expr_ try_string_ catch_string_ ...
      error_message_
  return;
elseif (N_ > matqueue('length'))
  errordlg(char('You entered too many variable names.', ...
      'Please try again.'), 'Workspace Transfer Error', 'on');
  clear var_string_ err_string_ new_prompt_ ...
      pound_ N_ fatal_error_flag_ i_ expr_ try_string_ catch_string_ ...
      error_message_
  return;
end
fatal_error_flag_ = 0;
for i_ = 1:N_
  expr_ = deblank(var_string_(i_, :));
  try
      assignin('base', expr_, matqueue('get'));
  catch
      fatal_error_flag_ = 1;
  end

  if (fatal_error_flag_)
    errordlg(char(sprintf('Error using "%s" as a workspace variable.', ...
  expr_), 'You will need to start over.'), ...
  'Workspace Transfer Error', 'on');
    set(matqdlg('find'), 'Visible', 'off');
    if (~isempty(get(matqdlg('find'),'UserData')))
      if (any(get(0,'Children') == get(matqdlg('find'),'UserData')))
  figure(get(matqdlg('find'),'UserData'));
      end
    end
    matqueue('clear');
    clear var_string_ err_string_ new_prompt_ ...
  pound_ N_ fatal_error_flag_ i_ expr_ try_string_ catch_string_ ...
  error_message_
    return;
  end
end
set(matqdlg('find'), 'Visible', 'off');
if (~isempty(get(matqdlg('find'),'UserData')))
  if (any(get(0,'Children') == get(matqdlg('find'),'UserData')))
    figure(get(matqdlg('find'),'UserData'));
  end
end

try
    char(get(get(matqdlg('find'),'CurrentObject'),'UserData'));
catch
    disp('Error evaluating button callback.')
end
close(matqdlg('find'));
clear var_string_ err_string_ new_prompt_ ...
    pound_ N_ fatal_error_flag_ i_ expr_ try_string_ catch_string_ error_message_ 

如下代码为 matqparse 。

function [m,error_str] = matqparse(str,flag)
%MATQPARSE Dialog entry parser for MATQDLG.
%   [M,ERROR_STR] = MATQPARSE(STR,FLAG) is a miniparser
%   for MATQDLG.
%   eg: 'abc de  f ghij' becomes [abc ]
%                                [de  ]
%                                [f   ]
%                                [ghij]
%   Uses either spaces, commas, semi-colons, or brackets
%   as separators.  Thus 'a 10*[b c] d' will crash. User
%   must instead say 'a [10*[b c]] d'.
%
% See also MATQDLG, MATQUEUE.

% Error checks
error_str = '';
if nargin==0
   error_str = getString(message('pde:matqparse:StringReqd'));
   return
elseif size(str,1)>1 | ~ischar(str)
   error_str = getString(message('pde:matqparse:SingleRowStringReqd'));
   return
end

if nargin<2
   flag = 1;
end

l = length(str);
m = '';
i = 1;
j = 1;
k = 1;
while k<=l
   % Check for missing [
   if str(k)==']'
      error_str = getString(message('pde:matqparse:UnmatchedRightBracket'));
      return
   elseif str(k)=='['
      % Check for missing ]
      index = find(str(k+1:l)==']');
      if isempty(index)
         error_str = getString(message('pde:matqparse:UnmatchedLeftBracket'));
         return
      else
         % Check for mismatched brackets between k+1 and last element
         index1 = find(str(k+1:l)=='[');
         l_index = length(index);
         l_index1 = length(index1);
         if l_index~=l_index1+1
            error_str = getString(message('pde:matqparse:BracketMismatch'));
            return
         else
            % Everything OK so far
            di = find([index1 index(l_index)+1]>index);
            end_ind = index(di(1));
            m_middle = ['[' matqparse(str(k+1:k+end_ind-1),2) ']'];
            if flag==1
               % m and m_end may be multiline matrices
               m_end = matqparse(str(k+end_ind+1:l),1); 
               m = char(m,m_middle,m_end);
            else
               % m and m_end will be single line
               m_end = matqparse(str(k+end_ind+1:l),2);
               m = [m m_middle m_end];
            end
            k = l+1;
         end
      end
   elseif any(str(k)==' ;,') & (flag==1)
      if j>1
         % Only reset to beginning of next row if 
         % NOT already at beginning of a row
         j=1;
         i = i+1;
      end
      k = k+1; % Increment index into str
   else
      m(i,j) = str(k);
      j = j+1; % Increment column of resultant matrix, m
      k = k+1; % Increment index into str
   end
end

% Since char of zero is end-of-string flag, change to blanks
if ~isempty(m)
   EndOfString = find(abs(m)==0);
   m(EndOfString) = char(' '*ones(size(EndOfString)));

   % Eliminate any empty rows
   if size(m,2)>1
      m  = m(find(any(m'~=' ')),:);
   end

end

% end matqparse

在生成的主文件求解程序末尾添加和修改为如下代码，即可导出数据。

clc
clear
close all
[pde_fig,ax]=pdeinit;
pdetool('appl_cb',1);
set(ax,'DataAspectRatio',[1.5 1 1]);
set(ax,'PlotBoxAspectRatio',[1 0.74375917767988253 0.74375917767988253]);
set(ax,'XLim',[-1.5 1.5]);
set(ax,'YLim',[-1 1]);
set(ax,'XTickMode','auto');
set(ax,'YTickMode','auto');

% Geometry description:
pdepoly([ -1,...
    1,...
    1,...
    0,...
    0,...
    -1,...
    ],...
    [ -1,...
    -1,...
    1,...
    1,...
    0,...
    0,...
    ],...
    'P1');
set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','P1')

% Boundary conditions:
pdetool('changemode',0)
pdesetbd(6,...
    'dir',...
    1,...
    '1',...
    '0')
pdesetbd(5,...
    'dir',...
    1,...
    '1',...
    '0')
pdesetbd(4,...
    'dir',...
    1,...
    '1',...
    '0')
pdesetbd(3,...
    'dir',...
    1,...
    '1',...
    '0')
pdesetbd(2,...
    'dir',...
    1,...
    '1',...
    '0')
pdesetbd(1,...
    'dir',...
    1,...
    '1',...
    '0')

% Mesh generation:
setappdata(pde_fig,'Hgrad',1.3);
setappdata(pde_fig,'refinemethod','regular');
setappdata(pde_fig,'jiggle',char('on','mean',''));
setappdata(pde_fig,'MesherVersion','preR2013a');
pdetool('initmesh')
pdetool('refine')

% PDE coefficients:
pdeseteq(4,...
    '1.0',...
    '0.0',...
    '10.0',...
    '1.0',...
    '0:10',...
    '0.0',...
    '0.0',...
    '[0 100]')
setappdata(pde_fig,'currparam',...
    ['1.0 ';...
    '0.0 ';...
    '10.0';...
    '1.0 '])

% Solve parameters:
setappdata(pde_fig,'solveparam',...
    char('0','1548','10','pdeadworst',...
    '0.5','longest','0','1E-4','','fixed','Inf'))

% Plotflags and user data strings:
setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 0 1]);
setappdata(pde_fig,'colstring','');
setappdata(pde_fig,'arrowstring','');
setappdata(pde_fig,'deformstring','');
setappdata(pde_fig,'heightstring','');

% Solve PDE:
pdetool('solve')
for flag=1:6
    % case: export variables to workspace
    pde_fig=findobj(allchild(0),'flat','Tag','PDETool');
    
    if flag==1
        % export geometry data:
        gd=get(findobj(get(pde_fig,'Children'),'flat',...
            'Tag','PDEMeshMenu'),'UserData');
        ns=getappdata(pde_fig,'objnames');
        evalhndl=findobj(get(pde_fig,'Children'),'flat','Tag','PDEEval');
        sf=get(evalhndl,'String');
        matqueue('put',gd,sf,ns)
        pstr='Variable names for geometry data, set formula, labels:';
        estr='gd sf ns';
    elseif flag==2
        % export decomposed list, boundary conditions:
        dl1=getappdata(pde_fig,'dl1');
        h=findobj(get(pde_fig,'Children'),'flat','Tag','PDEBoundMenu');
        bl=get(findobj(get(h,'Children'),'flat',...
            'Tag','PDEBoundMode'),'UserData');
        matqueue('put',dl1,bl)
        pstr='Variable names for decomposed geometry, boundary cond''s:';
        estr='g b';
    elseif flag==3
        % export mesh:
        h=findobj(get(pde_fig,'Children'),'flat','Tag','PDEMeshMenu');
        p=get(findobj(get(h,'Children'),'flat','Tag','PDEInitMesh'),...
            'UserData');
        e=get(findobj(get(h,'Children'),'flat','Tag','PDERefine'),...
            'UserData');
        t=get(findobj(get(h,'Children'),'flat','Tag','PDEMeshParam'),...
            'UserData');
        matqueue('put',p,e,t)
        pstr='Variable names for mesh data (points, edges, triangles):';
        estr='p e t';
    elseif flag==4
        % export PDE coefficients:
        params=get(findobj(get(pde_fig,'Children'),'Tag','PDEPDEMenu'),...
            'UserData');
        ns=getappdata(pde_fig,'ncafd');
        nc=ns(1); na=ns(2); nf=ns(3); nd=ns(4);
        c=params(1:nc,:);
        a=params(nc+1:nc+na,:);
        f=params(nc+na+1:nc+na+nf,:);
        d=params(nc+na+nf+1:nc+na+nf+nd,:);
        matqueue('put',c,a,f,d)
        pstr='Variable names for PDE coefficients:';
        estr='c a f d';
    elseif flag==5
        % export solution:
        u=get(findobj(get(pde_fig,'Children'),'flat','Tag','PDEPlotMenu'),...
            'UserData');
        l=get(findobj(get(pde_fig,'Children'),'flat','Tag','winmenu'),...
            'UserData');
        if isempty(l)
            pstr='Variable name for solution:';
            estr='u';
            matqueue('put',u)
        else
            pstr='Variable names for solution and eigenvalues:';
            estr='u l';
            matqueue('put',u,l)
        end
    elseif flag==6
        % export movie:
        M=getappdata(pde_fig,'movie');
        matqueue('put',M)
        pstr='Variable name for PDE solution movie:';
        estr='M';
    end
    pdeinfo('Change the variable name(s) if desired. OK when done.',0);
    %matqdlg('buffer2ws','Name','Export','PromptString',pstr,...
    %    'OKCallback','pdeinfo;','CancelCallback','pdeinfo;','EntryString',estr);
    
end

出现 You did not enter enough variable names. Please try again. 如何解决？

不要调用matqdlg('buffer2ws','Name','Export','PromptString',pstr,'OKCallback','pdeinfo;','CancelCallback','pdeinfo;','EntryString',estr);即可。

0.1 基础：编程调用 PDE 工具箱

有的朋友说，PDE 工具箱求解 PDE 生成的代码，运行的时候会跳出界面，一看就显得很没有 B 格，有没有办法纯代码操作呢？当然有，界面也只不过是一些代码的集合而已。不想要 PDE 工具箱的界面，又想快速地写出有限元代码，需要一点点代码和有限元基础。

由工具箱界面生成的代码，一定是和图形界面高度耦合的，我们想把图形界面去掉不显示，并不容易。所以我们考虑使用 MATLAB 脚本完全定义问题。举一个简单的例子来说明它的操作。

我们还是以拉普拉斯特征值为例：
− Δ u = λ u -\Delta u=\lambda u −Δu=λu

代码如下：

clc
clear
close all
model = createpde();%创建PDE模型
geometryFromEdges(model,@squareg);%从边界生成几何
pdegplot(model,'EdgeLabels','on')%可视化
ylim([-1.5,1.5])
axis equal
applyBoundaryCondition(model,'dirichlet','Edge',4,'u',0);%左边界 0 狄利克雷边界条件
applyBoundaryCondition(model,'neumann','Edge',[1,3],'g',0,'q',0);%上下边界 0 纽曼边界条件
applyBoundaryCondition(model,'neumann','Edge',2,'g',0,'q',-3/4);%由边界混合边界条件，\frac{\partial u}{\partial n}-\frac{3}{4} u=0
specifyCoefficients(model,'m',0,'d',1,'c',1,'a',0,'f',0);%指定系数，表示特征值问题
r = [-Inf,10];%找小于10的特征值和特征向量
generateMesh(model,'Hmax',0.05);%生成网格
results = solvepdeeig(model,r);%在指定范围求解特征值问题，找六个特征值
l = results.Eigenvalues;%获得特征值
u = results.Eigenvectors;%获得特征值对应的特征向量
pdeplot(model,'XYData',u(:,1));%画第一个特征函数
pdeplot(model,'XYData',u(:,length(l)));%画最后一个特征函数
%l(2) - l(1) - pi^2/4
%l(5) - l(1) - pi^2

上面用的是矩形区域。当然，更复杂的区域我们可以使用 decsg。区域的矩阵表示可以参考这个链接。

decsg 使用的简单示例如下：

clc
clear
close all
rect1 = [3
    4
    -1
    1
    1
    -1
    0
    0
    -0.5
    -0.5];
C1 = [1
    1
    -0.25
    0.25];
C2 = [1
    -1
    -0.25
    0.25];
C1 = [C1;zeros(length(rect1) - length(C1),1)];
C2 = [C2;zeros(length(rect1) - length(C2),1)];
gd = [rect1,C1,C2];
ns = char('rect1','C1','C2');
ns = ns';
sf = '(rect1+C1)-C2';
[dl,bt] = decsg(gd,sf,ns);

期间的刚度矩阵和质量矩阵也可以通过 assembleFEMatrices 获得。最后给一个区域稍微复杂一点的，通俗易懂的例子吧。顺便和直接把刚度矩阵和质量矩阵导出来调用 eigs 求解做个比较。

clc
clear
close all
%% 创建模型
model = createpde;
radius = 2;
g = decsg([1 0 0 radius]','C1',('C1')');%通过简单集合图形生成区域
geometryFromEdges(model,g);
pdegplot(model,'EdgeLabels','on')%可视化
axis equal
title 'Geometry with Edge Labels'
c = 1;a = 0;f = 0;d = 1;
specifyCoefficients(model,'m',0,'d',d,'c',c,'a',a,'f',f);
applyBoundaryCondition(model,'dirichlet','Edge',(1:4),'u',0);
generateMesh(model,'Hmax',0.2);
%% 通过导出的刚度矩阵求特征值
FEMatrices = assembleFEMatrices(model,'nullspace');
K = FEMatrices.Kc;
B = FEMatrices.B;
M = FEMatrices.M;
sigma = 10; 
numberEigenvalues = 5;
[eigenvectorsEigs,eigenvaluesEigs] = eigs(K,M,numberEigenvalues,sigma);
eigenvaluesEigs = diag(eigenvaluesEigs);
[maxEigenvaluesEigs,maxIndex] = max(eigenvaluesEigs);
eigenvectorsEigs = B*eigenvectorsEigs;
%% 通过工具箱直接求特征值
r = [min(eigenvaluesEigs)*0.99 max(eigenvaluesEigs)*1.01];
result = solvepdeeig(model,r);
eigenvectorsPde = result.Eigenvectors;
eigenvaluesPde = result.Eigenvalues;
%% 对比两种方法求出的特征值和特征向量的差距
eigenValueDiff = sort(eigenvaluesPde) - sort(eigenvaluesEigs);
fprintf('Maximum difference in eigenvalues from solvepdeeig and eigs: %e\n', ...
  norm(eigenValueDiff,inf));
%% 画所选范围最大特征值对应的特征函数
h = figure;
h.Position = [1 1 2 1].*h.Position;
subplot(1,2,1)
axis equal
pdeplot(model,'XYData', eigenvectorsEigs(:,maxIndex),'Contour','on')
title(sprintf('eigs eigenvector, eigenvalue: %12.4e', eigenvaluesEigs(maxIndex)))
xlabel('x')
ylabel('y')
subplot(1,2,2)
axis equal
pdeplot(model,'XYData',eigenvectorsPde(:,end),'Contour','on')
title(sprintf('solvepdeeig eigenvector, eigenvalue: %12.4e',eigenvaluesPde(end)))
xlabel('x')
ylabel('y')