⭐️前面的话⭐️
大家好!博主开辟了一个新的专栏——剑指offer,我要开始刷题了!这个专栏会介绍《剑指offer》书上所有的面试编程题。并且会分享一些我的刷题心得。由于博主水平有限,如有错误,欢迎指正,如果有更好的解题思路和算法可以分享给博主哦!一起加油!一起努力!
📒博客主页:未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创,CSDN首发!
📆首发时间:🌴2021年9月11日🌴
✉️坚持和努力一定能换来诗与远方!
💭参考书籍:📚《剑指offer第1版》,📚《剑指offer第2版》
💬参考在线编程网站:🌐牛客网🌐力扣
🙏作者水平很有限,如果发现错误,一定要及时告知作者哦!感谢感谢!
博主的码云gitee,平常博主写的程序代码都在里面。
📌导航小助手📌
- ⭐️剑指 Offer 21. 调整数组顺序使奇数位于偶数前面⭐️
- 🔐题目详情
- 💡解题思路
- 🔑源代码
- 🌱总结
⭐️剑指 Offer 21. 调整数组顺序使奇数位于偶数前面⭐️
🔐题目详情
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4] 也是正确的答案之一。
限制:
0 <= nums.length <= 50000
1 <= nums[i] <= 10000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/diao-zheng-shu-zu-shun-xu-shi-qi-shu-wei-yu-ou-shu-qian-mian-lcof/
💡解题思路
解决这道题肯定是需要用到奇偶判断的,除了使用模2法,还可以利用运算符&实现奇偶的判断。我们可以将目的数与1进行按位与操作,因为1的二进制序列只有末位是1其他位都为0,所以如果目的数的二进制序列末位为1,则按位与的结果为1否则为0,我们知道一个整数二进制序列末位为1为奇数,末位为0为偶数,所以目的数 & 1结果为1,表示目的数为奇数,结果为0,表示目的数为偶数。
方法1: 奇偶分别拷贝。
如果不考虑在原本的数组上进行修改,我们可以可以申请一个与原数组一样大的数组,创建双指针从数组的两头拷贝数组元素,左边拷贝奇数,右边拷贝偶数,直到填满数组为止!
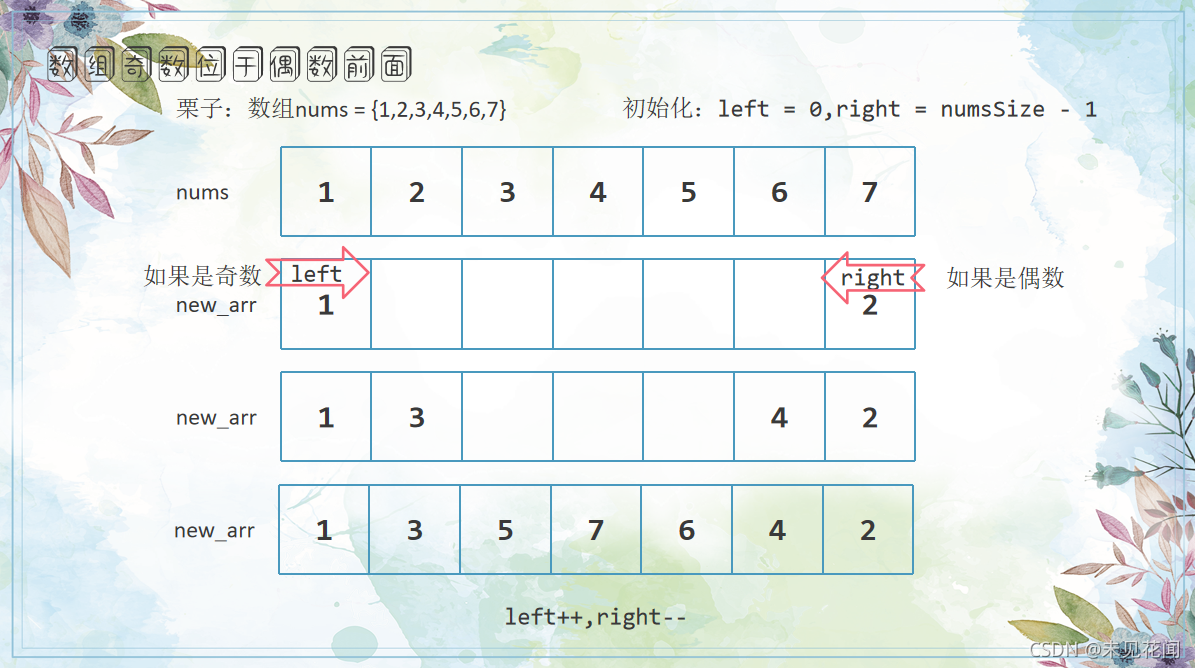
时间复杂度: O(N)
空间复杂度: O(N)
方法2: 双指针。假设目标数组为nums,利用左右两个指针left right,满足nums[left]为偶数,nums[right]为奇数,则交换这两个数!循环条件为left < right。
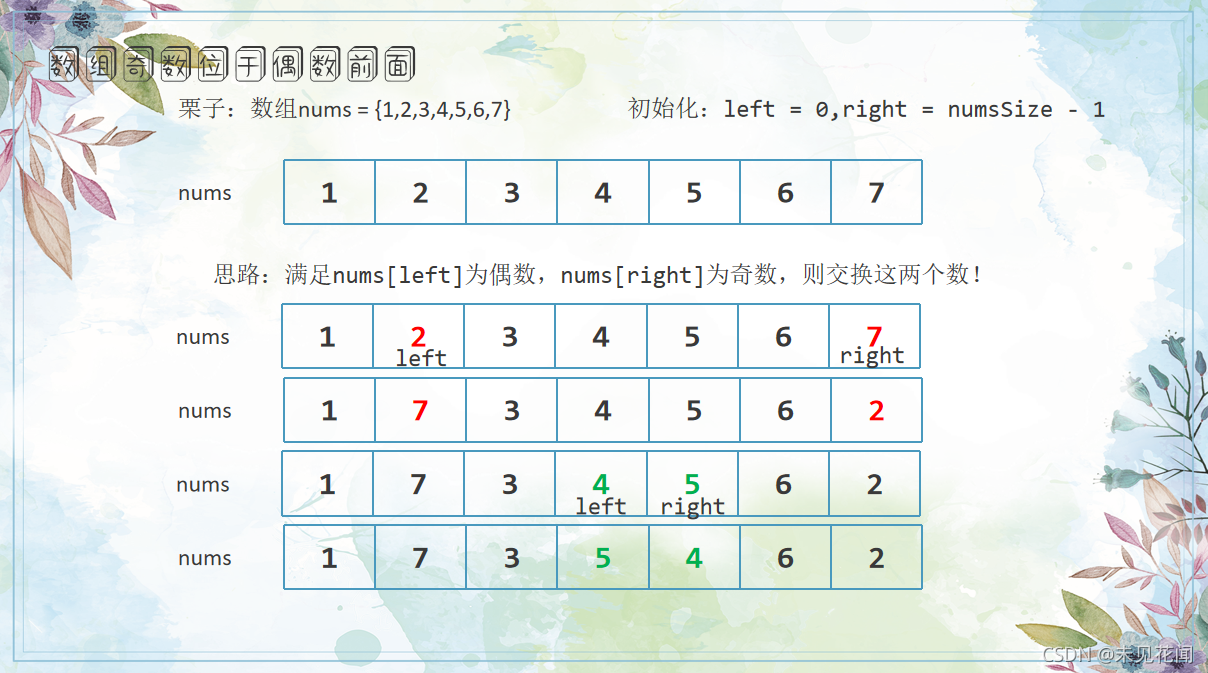
时间复杂度: O(N)
空间复杂度: O(1)
🔑源代码
编程语言:C语言
在线编程平台:力扣
//方法1
int* exchange(int* nums, int numsSize, int* returnSize){
int left = 0;
int right = numsSize - 1;
int* new_arr = (int*)malloc(sizeof(int) * numsSize);
int i = 0;
for (i = 0; i < numsSize; i++)
{
if (*(nums + i) & 1)
{
*(new_arr + left) =*(nums + i);//奇数存左边
left++;
}
else
{
*(new_arr + right) = *(nums + i);//偶数存右边
right--;
}
}
*returnSize = numsSize;
return new_arr;
}
int* exchange(int* nums, int numsSize, int* returnSize){
int left = 0;
int right = numsSize - 1;
//满足nums[left]为偶数,nums[right]为奇数,则交换这两个数!
while(left < right)
{
if (*(nums + left) % 2 == 0)
{
while (left < right)
{
if (*(nums + right) % 2 == 1)
{
int tmp = *(nums + left);
*(nums + left) = *(nums + right);
*(nums + right) = tmp;
right-- ;
break;
}
else
{
right--;
}
}
}
left++;
}
*returnSize = numsSize;
return nums;
}
🌱总结
首先,这道调整数组奇偶顺序问题,可以在数组本身进行调整,也可以通过判断奇偶按照特定的规则存入新数组中,如果空间足够多,时间上后者较优一点点,当然如果空间不够用,后者显然是不可用的,整体比较还是在数组本身调整较优。然后通过这道题,我们不要局限于调整奇偶顺序,因为这本质上还是奇偶数的判断,假设面试官需要我们使用一个函数实现多个功能,提高此函数的扩展性,鲁棒性,比如能实现调整奇偶数的顺序同时还能调整质数与非质数的顺序,调整负数与非负数的顺序等等。这些功能只需要改变判断的条件而不需要改变整体的程序框架,调整奇偶顺序是判断是否奇数(或偶数),调整质数与非质数顺序是判断是否为质数,调整负数与非负数的顺序是判断是否是负数等等。这时候我们可以给这个函数传入一个函数指针,这个函数指针所指向的函数用来判断是否是奇数,是否是质数,是否是负数等等,实现不同场景下不同条件的判断,这样我们仅仅需要改变传入的函数指针就能改变函数的功能,做到一个函数多个功能。