题目
描述
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例1
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2示例2
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5示例3
输入:nums1 = [0,0], nums2 = [0,0]
输出:0.00000示例4
输入:nums1 = [], nums2 = [1]
输出:1.00000示例5
输入:nums1 = [2], nums2 = []
输出:2.00000提示
(1)nums1.length == m
(2)nums2.length == n
(3)0 <= m <= 1000
(4)0 <= n <= 1000
(5)1 <= m + n <= 2000
(6)-106 <= nums1[i], nums2[i] <= 106
进阶
你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗?
解题思路
(1)将两个列表进行合并
(2)通过sort函数进行排序
(3)判断两个列表合并后的长度
(4)长度位奇数,那么中位数的index 为(len_list + 1) / 2
(5)长度为偶数的话,那么中位数的index为 len_list / 2
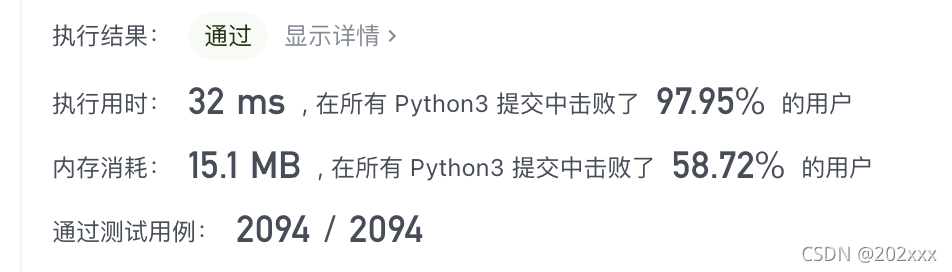
代码
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
num_list = nums1 + nums2
num_list.sort()
print(num_list)
if len(num_list)%2==0:
index = int(len(num_list)/2)
return (num_list[index] + num_list[index-1])/2
else:
index = int((len(num_list)-1)/2)
return num_list[index]进阶
(1)二分法查找
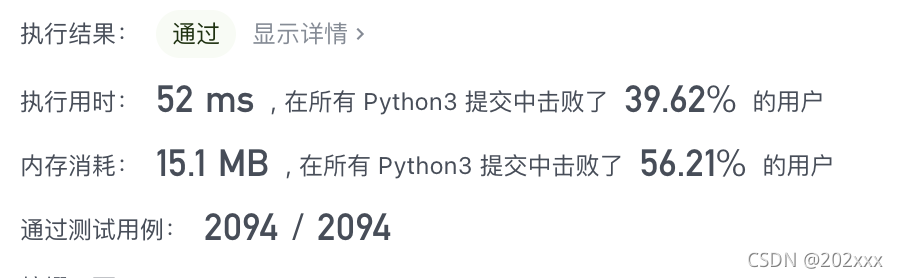
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
def getKthElement(k):
"""
- 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
- 这里的 "/" 表示整除
- nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
- nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
- 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
- 这样 pivot 本身最大也只能是第 k-1 小的元素
- 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组
- 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组
- 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
"""
index1, index2 = 0, 0
while True:
# 特殊情况
if index1 == m:
return nums2[index2 + k - 1]
if index2 == n:
return nums1[index1 + k - 1]
if k == 1:
return min(nums1[index1], nums2[index2])
# 正常情况
newIndex1 = min(index1 + k // 2 - 1, m - 1)
newIndex2 = min(index2 + k // 2 - 1, n - 1)
pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
if pivot1 <= pivot2:
k -= newIndex1 - index1 + 1
index1 = newIndex1 + 1
else:
k -= newIndex2 - index2 + 1
index2 = newIndex2 + 1
m, n = len(nums1), len(nums2)
totalLength = m + n
if totalLength % 2 == 1:
return getKthElement((totalLength + 1) // 2)
else:
return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2(2)划分数组
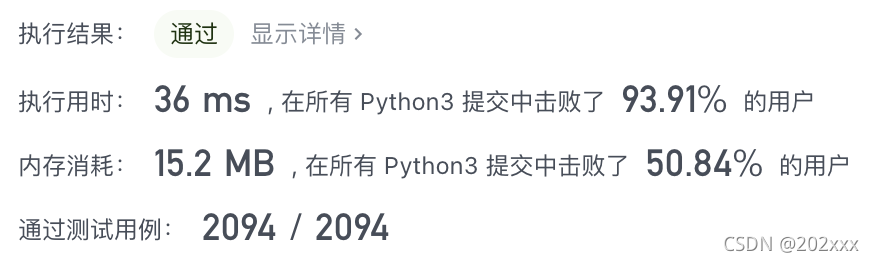
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
if len(nums1) > len(nums2):
return self.findMedianSortedArrays(nums2, nums1)
infinty = 2**40
m, n = len(nums1), len(nums2)
left, right = 0, m
# median1:前一部分的最大值
# median2:后一部分的最小值
median1, median2 = 0, 0
while left <= right:
# 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
# // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
i = (left + right) // 2
j = (m + n + 1) // 2 - i
# nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
nums_im1 = (-infinty if i == 0 else nums1[i - 1])
nums_i = (infinty if i == m else nums1[i])
nums_jm1 = (-infinty if j == 0 else nums2[j - 1])
nums_j = (infinty if j == n else nums2[j])
if nums_im1 <= nums_j:
median1, median2 = max(nums_im1, nums_jm1), min(nums_i, nums_j)
left = i + 1
else:
right = i - 1
return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1Reference
题库 - 力扣 (LeetCode) 全球极客挚爱的技术成长平台