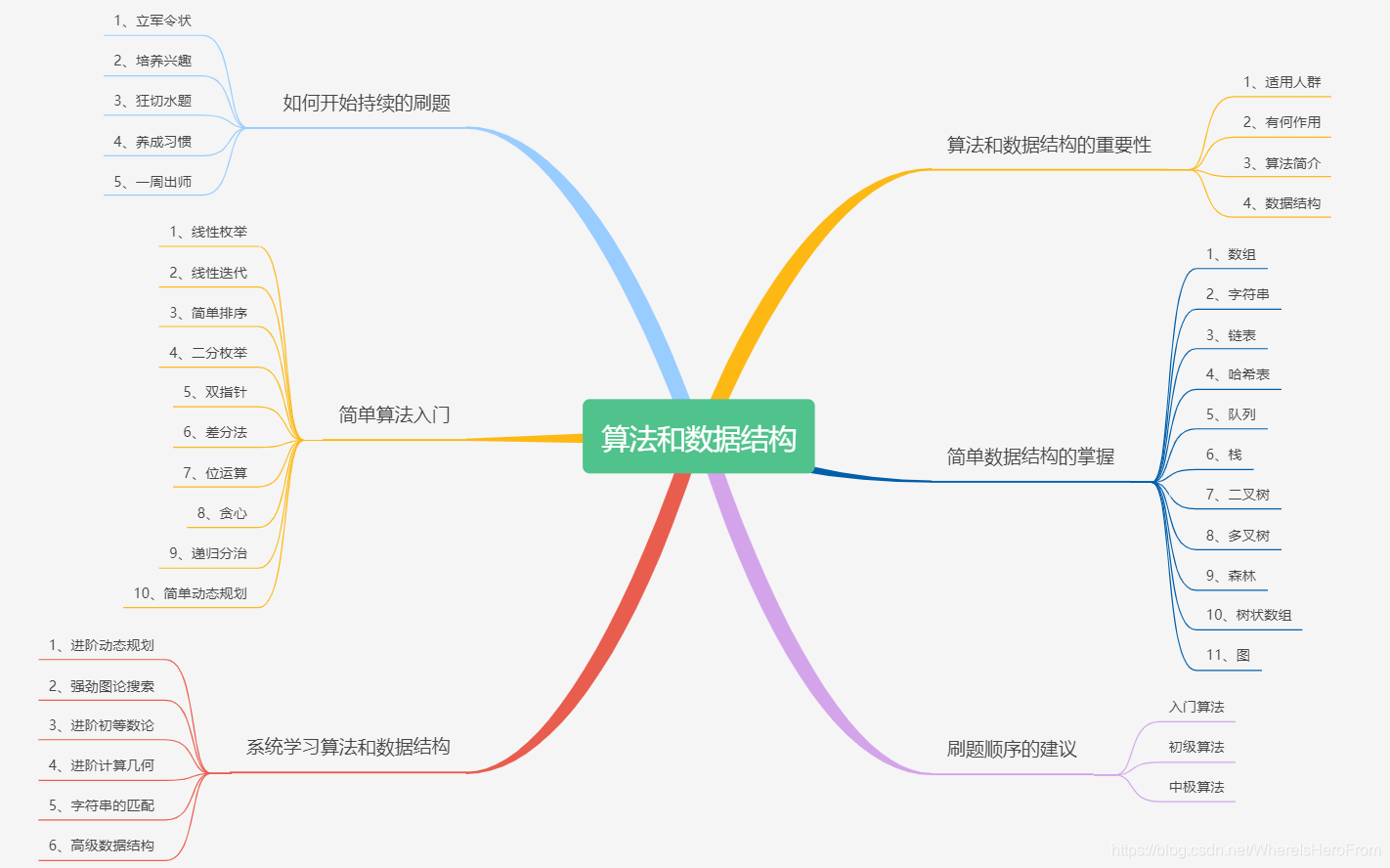
文章目录
- 1️⃣前言:追忆我的刷题经历
- 2️⃣算法和数据结构的重要性
- 👪1、适用人群
- 🎾2、有何作用
- 📜3、算法简介
- 🌲4、数据结构
- 3️⃣如何开始持续的刷题
- 📑1、立军令状
- 👩❤️👩2、培养兴趣
- 🚿3、狂切水题
- 💪🏻4、养成习惯
- 🈵5、一周出师
- 4️⃣简单数据结构的掌握
- 🚂1、数组
- 🎫2、字符串
- 🎇3、链表
- 🌝4、哈希表
- 👨👩👧5、队列
- 👩👩👦👦6、栈
- 🌵7、二叉树
- 🌳8、多叉树
- 🌲9、森林
- 🍀10、树状数组
- 🌍11、图
- 5️⃣简单算法的入门
- 💨1、线性枚举
- 🥖2、线性迭代
- 💤3、简单排序
- 🥂4、二分枚举
- 🥢5、双指针
- 🍴6、差分法
- 🅱7、位运算
- 🧡8、贪心
- ♈9、递归分治
- 🚊10、简单动态规划
- 6️⃣刷题顺序的建议
- 👨👦1、入门算法
- 👩👧👦2、初级算法
- 👩👩👧👦3、中级算法
- 7️⃣系统学习算法和数据结构
- 🚍1、进阶动态规划
- 🪐2、强劲图论搜索
- 0️⃣3、进阶初等数论
- 🛑4、进阶计算几何
- 📏5、字符串的匹配
- 🎄6、高級数据结构
1️⃣前言:追忆我的刷题经历
大学的时候比较疯狂,除了上课的时候,基本都是在机房刷题,当然,有时候连上课都在想题目,纸上写好代码,一下课就冲进机房把代码敲了,目的很单纯,为了冲排行榜,就像玩游戏一样,享受霸榜的快感。
当年主要是在 杭电OJ (HDOJ) 和 北大OJ(POJ) 这两个在线平台上刷题,那时候应该还没有(LeetCode、洛谷、牛客 这些主流的刷题网站),后来参加工作以后,剩余的时间不多了,也就没怎么刷了, 但是 算法思维 也就是靠上大学那四年锻炼出来的。
当年题目少,刷题的人也少,所以勉强还冲到过第一,现在去看已经 58 名了,可见 长江后浪推前浪,前浪 S 在沙滩上。时势造英雄啊!
北大人才辈出,相对题目也比较难,所以明显有点 心有余而力不足 的感觉,刷的相对就少很多,而且这个 OJ 也没什么人维护了,看我的签名,当时竟然还想着给博客引点流,现在估计都没什么人去那个网站了吧,如果有,记得评论区告诉我,一起缅怀一下逝去的青春。🙉饭不食,水不饮,题必须刷🙉
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
LeetCode 太难?先看简单题! 🧡《C语言入门100例》🧡
LeetCode 太简单?算法学起来! 🌌《夜深人静写算法》🌌

2️⃣算法和数据结构的重要性
👪1、适用人群
- 这篇文章会从 「算法和数据结构」 零基础开始讲,所以,如果你是算法大神,可以尽情在评论区嘲讽我哈哈,目的当然是帮助想要涉足算法领域,或者正在找工作的朋友,以及将要找工作的大学生,更加有效快速的掌握算法思维,能够在职场面试和笔试中一展身手。
- 这篇文章中,我会着重讲解一些常见的 「算法和数据结构」 的设计思想,并且配上动图。主要针对面试中常见的问题和新手朋友们比较难理解的点进行解析。当然,后面也会给出面向算法竞赛的提纲,如果有兴趣深入学习的欢迎在评论区留言,一起成长交流。
- 零基础学算法的最好方法,莫过于刷题了。任何事情都是需要坚持的,刷题也一样,没有刷够足够的题,就很难做出系统性的总结。所以上大学的时候,我花了三年的时间来刷题, 工作以后还是会抽点时间出来刷题。
千万不要用工作忙来找借口,时间挤一挤总是有的。
- 我现在上班地铁上一个小时,下班地铁又是一个小时。比如这篇文章的起草,就是在 地铁 上完成的。如何利用这两个小时的时间,做一些有建设性的事情,才是最重要的。刷抖音一个小时过得很快,刷题也是同样的道理。
- 当然,每天不需要花太多时间在这个上面,把这个事情做成一个规划,按照长期去推进。反正也没有 KPI 压力,就当成是工作之余的一种消遣,还能够提升思维能力。
所以,无论你是 小学生,中学生,高中OIer,大学ACMer,职场人士,只要想开始,一切都不会太晚!
🎾2、有何作用
- 我们平常使用的 智能手机、搜索引擎、网站、操作系统、游戏、软件、人工智能,都大量地应用了 「算法与数据结构」 的知识,以及平时你用到的各种库的底层实现,也是通过各种算法和数据结构组合出来的,所以可以说,有程序的地方,就有
江湖算法,有算法就一定会有对应的数据结构。 - 如果你只是想学会写代码,或许 「算法与数据结构」 并不是那么重要,但是想要往更深一步发展,「算法与数据结构」 是必不可少的。
现在一些主流的大厂,在面试快结束的时候都会 奉上一道算法题,如果你敲不出来,可能你的 offer 年包就打了 七折,或者直接与 offer 失之交臂,都是有可能的(因为我自己也是万恶的面试官,看到候选人的算法题写不出来我也是操碎了心,但是我一般会给足容错,比如给三个算法题,挑一个写,任意写出一个都行)。
- 当然,它不能完全代表你的编码能力,因为有些算法确实是很巧妙,加上紧张的面试氛围,想不出来其实也是正常的,但是你能确保面试官是这么想的吗?我们要做的是十足的准备,既然决定出来,offer 当然是越高越好,毕竟大家都要养家糊口,房价又这么贵,如果能够在算法这一块取得先机,也不失为一个捷径。
所以,你问我算法和数据结构有什么用?我可以很明确的说,和你的年薪息息相关。
- 当然,面试中 「算法与数据结构」 知识的考察只是面试内容的一部分。其它还有很多面试要考察的内容,当然不是本文主要核心内容,这里就不做展开了。
📜3、算法简介
- 算法是什么东西?
- 它是一种方法,一种解决问题的方案。
- 举个例子,你现在要去上班,可以选择 走路、跑步、坐公交、坐地铁、自己开车 等等,这些都是解决方案。但是它们都会有一些衡量指标,让你有一个权衡,最后选择你认为最优的策略去做。
- 而衡量的指标诸如:时间消耗、金钱消耗、是否需要转车、是否可达 等等。
时间消耗就对应了:时间复杂度
金钱消耗就对应了:空间复杂度
是否可达就对应了:算法可行性
- 当然,是否需要转车,从某种程度上都会影响 时间复杂度 或者 空间复杂度。
🌲4、数据结构
- 对于实现某个算法,我们往往会用到一些数据结构。
- 因为我们通常不能一下子把数据处理完,更多的时候需要先把它们放在一个容器或者说缓存里面,等到一定的时刻再把它们拿出来。
- 这其实是一种 「空间换时间」 思想的体现, 恰当使用数据结构可以帮助我们高效地处理数据。
- 常用的一些数据结构如下:
| 数据结构 | 应用场景 |
|---|---|
| 数组 | 线性存储、元素为任意相同类型、随机访问 |
| 字符串 | 线性存储、元素为字符、结尾字符、随机访问 |
| 链表 | 链式存储、快速删除 |
| 栈 | 先进后出 |
| 队列 | 先进先出 |
| 哈希表 | 随机存储、快速增删改查 |
| 二叉树 | 对数时间增删改查,二叉查找树、线段树 |
| 多叉树 | B/B+树 硬盘树、字典树 字符串前缀匹配 |
| 森林 | 并查集 快速合并数据 |
| 树状数组 | 单点更新,成段求和 |
- 为什么需要引入这么多数据结构呢?
答案是:任何一种数据结构是不是 完美的。所以我们需要根据对应的场景,来采用对应的数据结构,具体用哪种数据结构,需要通过刷题不断刷新经验,才能总结出来。
3️⃣如何开始持续的刷题
- 有朋友告诉我,题目太难了,根本不会做,每次都是看别人的解题报告。
📑1、立军令状
- 所谓 「军令状」,其实就是给自己定一个目标,给自己树立一个目标是非常重要的,有 「目标才会有方向,有目标才会有动力,有目标才会有人生的意义」 。而军令状是贬义的,如果不达成就会有各种惩罚,所以其实你是心不甘情不愿的,于是这件事情其实是无法持久下去的。
事实证明,立军令状是不可取的。
- 啊这……所以我们还是要采用一些能够持久下去的方法。
👩❤️👩2、培养兴趣
- 为了让这件事情能够持久下去,一定要培养出兴趣,适时的给自己一些正反馈。正反馈的作用就是每过一个周期,如果效果好,就要有奖励,这个奖励机制可以自己设定,但是 「不能作弊」 ,一旦作弊就像单机游戏修改数值,流失是迟早的事。
- 举个例子,我们可以给每天制定一些 「不一样的目标和奖励」 ,比如下图所示:
| 刷题的第?天 | 目标题数 | 是否完成 | 完成奖励 |
|---|---|---|---|
| 1 | 1 | ? | 攻击力 + 10 |
| 2 | 1 | ? | 防御力 + 10 |
| 3 | 2 | ? | 出去吃顿好的 |
| 4 | 2 | ? | 攻击力 + 29 |
| 5 | 3 | ? | 防御力 + 60 |
| 6 | 1 | ? | 攻击力 + 20 |
| 7 | 4 | ? | 出去吃顿好的 |
| 8 | 1 | ? | 防御力 + 50 |
- 当然,这个完成奖励你可以自己定,总而言之,要是对你有诱惑的奖励才是有意义的。
🚿3、狂切水题
- 刚开始刷的 300 题一定都是 「水题」 ,刷 「水题」 的目的是让你养成一个每天刷题的习惯。久而久之,不刷题的日子会变得无比煎熬。当然,刷着刷着,你会发现,水题会越来越多,因为刷题的过程中,你已经无形中不断成长起来了。
- 至少这个方法我用过,非常灵验!推荐刷题从水题开始。
如果不知道哪里有水题,推荐:
C语言入门水题:《C语言入门100例》
C语言算法水题:《LeetCode算法全集》
💪🏻4、养成习惯
- 相信如果切了 300 个 「水题」 以后,刷题自然而然就成了习惯,想放弃都难。这个专业上讲,其实叫 沉没成本。有兴趣的可以自行百度,这里就不再累述了。
🈵5、一周出师
- 基本上如果能够按照这样的计划去执行,一周以后,一定会有收获,没有收获的话,可以来找我。
4️⃣简单数据结构的掌握
🚂1、数组
内存结构:内存空间连续
实现难度:简单
下标访问:支持
分类:静态数组、动态数组
插入时间复杂度: O ( n ) O(n) O(n)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( n ) O(n) O(n)
🎫2、字符串
内存结构:内存空间连续,类似字符数组
实现难度:简单,一般系统会提供一些方便的字符串操作函数
下标访问:支持
插入时间复杂度: O ( n ) O(n) O(n)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( n ) O(n) O(n)
🎇3、链表
内存结构:内存空间连续不连续,看具体实现
实现难度:一般
下标访问:不支持
分类:单向链表、双向链表、循环链表、DancingLinks
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( 1 ) O(1) O(1)
🌝4、哈希表
内存结构:哈希表本身连续,但是衍生出来的结点逻辑上不连续
实现难度:一般
下标访问:不支持
分类:正数哈希、字符串哈希、滚动哈希
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度: O ( 1 ) O(1) O(1)
删除时间复杂度: O ( 1 ) O(1) O(1)
- 哈希表相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(九)- 哈希表
👨👩👧5、队列
内存结构:看用数组实现,还是链表实现
实现难度:一般
下标访问:不支持
分类:FIFO、单调队列、双端队列
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度:理论上不支持
删除时间复杂度: O ( 1 ) O(1) O(1)
- 队列相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(十)- 单向广搜
👩👩👦👦6、栈
内存结构:看用数组实现,还是链表实现
实现难度:一般
下标访问:不支持
分类:FILO、单调栈
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度:理论上不支持
删除时间复杂度: O ( 1 ) O(1) O(1)
- 栈相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(十一)- 单调栈
🌵7、二叉树
优先队列 是 堆实现的,所以也属于 二叉树 范畴。它和队列不同,不属于线性表。
内存结构:内存结构一般不连续,但是有时候实现的时候,为了方便,一般是物理连续,逻辑不连续
实现难度:较难
下标访问:不支持
分类:二叉树 和 多叉树
插入时间复杂度:看情况而定
查找时间复杂度:理论上 O ( l o g 2 n ) O(log_2n) O(log2n)
删除时间复杂度:看情况而定
🌳8、多叉树
内存结构:内存结构一般不连续,但是有时候实现的时候,为了方便,一般是物理连续,逻辑不连续
实现难度:较难
下标访问:不支持
分类:二叉树 和 多叉树
插入时间复杂度:看情况而定
查找时间复杂度:理论上 O ( l o g 2 n ) O(log_2n) O(log2n)
删除时间复杂度:看情况而定
- 一种经典的多叉树是字典树,可以参考我的这篇文章:
- 夜深人静写算法(七)- 字典树
🌲9、森林
- 比较经典的森林是:并查集,可以参考我的这篇文章:
- 夜深人静写算法(五)- 并查集
🍀10、树状数组
- 树状数组是用来做 单点更新,成端求和 的问题的,有关于它的内容,可以参考:
- 夜深人静写算法(十三)- 树状数组
🌍11、图
内存结构:不一定
实现难度:难
下标访问:不支持
分类:有向图、无向图
插入时间复杂度:根据算法而定
查找时间复杂度:根据算法而定
删除时间复杂度:根据算法而定
1、图的概念
- 在讲解最短路问题之前,首先需要介绍一下计算机中图(图论)的概念,如下:
- 图 G G G 是一个有序二元组 ( V , E ) (V,E) (V,E),其中 V V V 称为顶点集合, E E E 称为边集合, E E E 与 V V V 不相交。顶点集合的元素被称为顶点,边集合的元素被称为边。
- 对于无权图,边由二元组 ( u , v ) (u,v) (u,v) 表示,其中 u , v ∈ V u, v \in V u,v∈V。对于带权图,边由三元组 ( u , v , w ) (u,v, w) (u,v,w) 表示,其中 u , v ∈ V u, v \in V u,v∈V, w w w 为权值,可以是任意类型。
- 图分为有向图和无向图,对于有向图, ( u , v ) (u, v) (u,v) 表示的是 从顶点 u u u 到 顶点 v v v 的边,即 u → v u \to v u→v;对于无向图, ( u , v ) (u, v) (u,v) 可以理解成两条边,一条是 从顶点 u u u 到 顶点 v v v 的边,即 u → v u \to v u→v,另一条是从顶点 v v v 到 顶点 u u u 的边,即 v → u v \to u v→u;
2、图的存储
- 对于图的存储,程序实现上也有多种方案,根据不同情况采用不同的方案。接下来以图二-3-1所表示的图为例,讲解四种存储图的方案。

1)邻接矩阵
- 邻接矩阵是直接利用一个二维数组对边的关系进行存储,矩阵的第 i i i 行第 j j j 列的值 表示 i → j i \to j i→j 这条边的权值;特殊的,如果不存在这条边,用一个特殊标记 ∞ \infty ∞ 来表示;如果 i = j i = j i=j,则权值为 0 0 0。
- 它的优点是:实现非常简单,而且很容易理解;缺点也很明显,如果这个图是一个非常稀疏的图,图中边很少,但是点很多,就会造成非常大的内存浪费,点数过大的时候根本就无法存储。
- [ 0 ∞ 3 ∞ 1 0 2 ∞ ∞ ∞ 0 3 9 8 ∞ 0 ] \left[ \begin{matrix} 0 & \infty & 3 & \infty \\ 1 & 0 & 2 & \infty \\ \infty & \infty & 0 & 3 \\ 9 & 8 & \infty & 0 \end{matrix} \right] ⎣⎢⎢⎡01∞9∞0∞8320∞∞∞30⎦⎥⎥⎤
2)邻接表
- 邻接表是图中常用的存储结构之一,采用链表来存储,每个顶点都有一个链表,链表的数据表示和当前顶点直接相邻的顶点的数据 ( v , w ) (v, w) (v,w),即 顶点 和 边权。
- 它的优点是:对于稀疏图不会有数据浪费;缺点就是实现相对邻接矩阵来说较麻烦,需要自己实现链表,动态分配内存。
- 如图所示,
d
a
t
a
data
data 即
(
v
,
w
)
(v, w)
(v,w) 二元组,代表和对应顶点
u
u
u 直接相连的顶点数据,
w
w
w 代表
u
→
v
u \to v
u→v 的边权,
n
e
x
t
next
next 是一个指针,指向下一个
(
v
,
w
)
(v, w)
(v,w) 二元组。

- 在 C++ 中,还可以使用 vector 这个容器来代替链表的功能;
vector<Edge> edges[maxn];
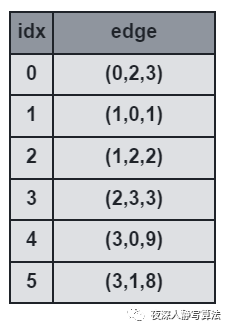
3)前向星
- 前向星是以存储边的方式来存储图,先将边读入并存储在连续的数组中,然后按照边的起点进行排序,这样数组中起点相等的边就能够在数组中进行连续访问了。
- 它的优点是实现简单,容易理解;缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序,带来了时间开销,实用性也较差,只适合离线算法。
- 如图所示,表示的是三元组
(
u
,
v
,
w
)
(u, v, w)
(u,v,w) 的数组,
i
d
x
idx
idx 代表数组下标。
- 那么用哪种数据结构才能满足所有图的需求呢?
- 接下来介绍一种新的数据结构 —— 链式前向星。
4)链式前向星
- 链式前向星和邻接表类似,也是链式结构和数组结构的结合,每个结点 i i i 都有一个链表,链表的所有数据是从 i i i 出发的所有边的集合(对比邻接表存的是顶点集合),边的表示为一个四元组 ( u , v , w , n e x t ) (u, v, w, next) (u,v,w,next),其中 ( u , v ) (u, v) (u,v) 代表该条边的有向顶点对 u → v u \to v u→v, w w w 代表边上的权值, n e x t next next 指向下一条边。
- 具体的,我们需要一个边的结构体数组
edge[maxm],maxm表示边的总数,所有边都存储在这个结构体数组中,并且用head[i]来指向 i i i 结点的第一条边。 - 边的结构体声明如下:
struct Edge {
int u, v, w, next;
Edge() {}
Edge(int _u, int _v, int _w, int _next) :
u(_u), v(_v), w(_w), next(_next)
{
}
}edge[maxm];
- 初始化所有的
head[i] = -1,当前边总数edgeCount = 0; - 每读入一条
u
→
v
u \to v
u→v 的边,调用
addEdge(u, v, w),具体函数的实现如下:
void addEdge(int u, int v, int w) {
edge[edgeCount] = Edge(u, v, w, head[u]);
head[u] = edgeCount++;
}
- 这个函数的含义是每加入一条边 ( u , v , w ) (u, v, w) (u,v,w),就在原有的链表结构的首部插入这条边,使得每次插入的时间复杂度为 O ( 1 ) O(1) O(1),所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现,空间上没有浪费,时间上也是最小开销。
- 调用的时候只要通过
head[i]就能访问到由 i i i 出发的第一条边的编号,通过编号到edge数组进行索引可以得到边的具体信息,然后根据这条边的next域可以得到第二条边的编号,以此类推,直到next域为 -1 为止。
for (int e = head[u]; ~e; e = edges[e].next) {
int v = edges[e].v;
ValueType w = edges[e].w;
...
}
- 文中的
~e等价于e != -1,是对e进行二进制取反的操作(-1 的的补码二进制全是 1,取反后变成全 0,这样就使得条件不满足跳出循环)。
5️⃣简单算法的入门

- 入门十大算法是 线性枚举、线性迭代、简单排序、二分枚举、双指针、差分法、位运算、贪心、分治递归、简单动态规划。
- 对于这十大算法,我会逐步更新道这个专栏里面:《LeetCode算法全集》。
💨1、线性枚举
- 枚举一般可以理解成一个循环,具体循环里面做什么事情,要根据实际问题而定,举个例子:
LeetCode 344. 反转字符串
【例题1】编写一个函数,将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。必须原地修改输入数组、使用 O ( 1 ) O(1) O(1) 的额外空间解决这一问题。
样例输入: [ ‘ ’ a ” , “ b ” , “ c ” ] [‘’a”, “b”, “c”] [‘’a”,“b”,“c”]
样例输出: [ “ c ” , “ b ” , “ a ” ] [ “c”, “b”, “a”] [“c”,“b”,“a”]
a. 思路分析
翻转的含义,相当于就是 第一个字符 和 最后一个交换,第二个字符 和 最后第二个交换,… 以此类推,所以我们首先实现一个交换变量的函数
swap,然后再枚举 第一个字符、第二个字符、第三个字符 …… 即可。
对于第 i i i 个字符,它的交换对象是 第 l e n − i − 1 len-i-1 len−i−1 个字符 (其中 l e n len len 为字符串长度)。swap函数的实现,可以参考:《C语言入门100例》 - 例2 | 交换变量。
b. 时间复杂度
- 线性枚举为 O ( n ) O(n) O(n),交换变量为 O ( 1 ) O(1) O(1),两个过程是相乘的关系,所以整个算法的时间复杂度为 O ( n ) O(n) O(n)。
c. 代码详解
class Solution {
public:
void swap(char& a, char& b) { // (1)
char tmp = a;
a = b;
b = tmp;
}
void reverseString(vector<char>& s) {
int len = s.size();
for(int i = 0; i < len / 2; ++i) { // (2)
swap(s[i], s[len-i-1]);
}
}
};
-
(
1
)
(1)
(1) 实现一个变量交换的函数,其中
&是C++中的引用,在函数传参是经常用到,被称为:引用传递(pass-by-reference),即被调函数的形式参数虽然也作为局部变量在堆栈中开辟了内存空间
,但是这时存放的是由主调函数放进来的实参变量的地址。被调函数对形参的任何操作都被处理成间接寻址,即通过堆栈中存放的地址访问主调函数中的实参变量。
简而言之,函数调用的参数,可以传引用,从而使得函数返回时,传参值的改变依旧生效。
- ( 2 ) (2) (2) 这一步是做的线性枚举,注意枚举范围是 [ 0 , l e n / 2 − 1 ] [0, len/2-1] [0,len/2−1]。
🥖2、线性迭代
- 每一次对过程的重复称为一次 “迭代”,而每一次迭代得到的结果会作为下一次迭代的初始值,周而复始,直到问题全部解决。
LeetCode 206. 反转链表
【例题2】给定单链表的头节点 h e a d head head ,要求反转链表,并返回反转后的链表头。
样例输入: [ 1 , 2 , 3 , 4 ] [1,2,3,4] [1,2,3,4]
样例输出: [ 4 , 3 , 2 , 1 ] [4, 3, 2, 1] [4,3,2,1]
- c++ 版本给出的基础框架代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
}
};
- 这里引入了一种数据结构 链表
ListNode; - 成员有两个:数据域
val和指针域next。 - 返回的是链表头结点;
a. 思路分析
- 这个问题,我们可以采用头插法,即每次拿出第 2 个节点插到头部,拿出第 3 个节点插到头部,拿出第 4 个节点插到头部,… 拿出最后一个节点插到头部。
- 于是整个过程可以分为两个步骤:删除第 i i i 个节点,将它放到头部,反复迭代 i i i 即可。
- 如图所示:

- 我们发现,图中的蓝色指针永远固定在最开始的链表头结点上,那么可以以它为契机,每次删除它的
next,并且插到最新的头结点前面,不断改变头结点head的指向,迭代 n − 1 n-1 n−1 次就能得到答案了。
b. 时间复杂度
- 每个结点只会被访问一次,执行一次头插操作,总共 n n n 个节点的情况下,时间复杂度 O ( n ) O(n) O(n)。
c. 代码详解
class Solution {
ListNode *removeNextAndReturn(ListNode* now) { // (1)
if(now == nullptr || now->next == nullptr) {
return nullptr; // (2)
}
ListNode *retNode = now->next; // (3)
now->next = now->next->next; // (4)
return retNode;
}
public:
ListNode* reverseList(ListNode* head) {
ListNode *doRemoveNode = head; // (5)
while(doRemoveNode) { // (6)
ListNode *newHead = removeNextAndReturn(doRemoveNode); // (7)
if(newHead) { // (8)
newHead->next = head;
head = newHead;
}else {
break; // (9)
}
}
return head;
}
};
-
(
1
)
(1)
(1)
ListNode *removeNextAndReturn(ListNode* now)函数的作用是删除now的next节点,并且返回; - ( 2 ) (2) (2) 本身为空或者下一个节点为空,返回空;
- ( 3 ) (3) (3) 将需要删除的节点缓存起来,供后续返回;
- ( 4 ) (4) (4) 执行删除 now->next 的操作;
-
(
5
)
(5)
(5)
doRemoveNode指向的下一个节点是将要被删除的节点,所以doRemoveNode需要被缓存起来,不然都不知道怎么进行删除; - ( 6 ) (6) (6) 没有需要删除的节点了就结束迭代;
- ( 7 ) (7) (7) 删除 doRemoveNode 的下一个节点并返回被删除的节点;
- ( 8 ) (8) (8) 如果有被删除的节点,则插入头部;
-
(
9
)
(9)
(9) 如果没有,则跳出迭代。

💤3、简单排序
- 既然是入门,千万不要去看快排、希尔排序这种冷门排序。
- 冒泡排序、选择排序、简单插入排序 原理好懂,先看懂再说,其他不管。因为这三者都是基于枚举的。
- C中有现成
qsort排序函数,C++中有现成sort排序函数,直接拿来用,等算法进阶时再回头来看快速排序的算法实现。
【例题3】LeetCode 88. 合并两个有序数组
【例题3】给你两个有序整数数组 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2,请你将 n u m s 2 nums2 nums2 合并到 n u m s 1 nums1 nums1 中,使 n u m s 1 nums1 nums1 成为一个有序数组。初始化 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2 的元素数量分别为 m m m 和 n n n 。你可以假设 n u m s 1 nums1 nums1 的空间大小等于 m + n m + n m+n,这样它就有足够的空间保存来自 n u m s 2 nums2 nums2 的元素。
样例输入: n u m s 1 = [ 1 , 2 , 3 , 0 , 0 , 0 ] , m = 3 , n u m s 2 = [ 2 , 5 , 6 ] , n = 3 nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 nums1=[1,2,3,0,0,0],m=3,nums2=[2,5,6],n=3
样例输出: [ 1 , 2 , 2 , 3 , 5 , 6 ] [1,2,2,3,5,6] [1,2,2,3,5,6]
a. 思路分析
这个题别想太多,直接把第二个数组的元素加到第一个数组元素的后面,然后直接排序就成。
b. 时间复杂度
- STL 排序函数的时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n),遍历的时间复杂度为 O ( n ) O(n) O(n),所以总的时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。
c. 代码详解
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
for(int i = m; i < n + m; ++i) {
nums1[i] = nums2[i-m]; // (1)
}
sort(nums1.begin(), nums1.end()); // (2)
}
};
- ( 1 ) (1) (1) 简单合并两个数组;
- ( 2 ) (2) (2) 对数组1进行排序;
只要能够达到最终的结果, O ( n ) O(n) O(n) 和 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) 的差距其实并没有那么大。
🥂4、二分枚举
- 二分一般指二分查找,当然有时候也指代二分枚举。
LeetCode 704. 二分查找
【例题4】给定 n ( 1 ≤ n ≤ 1 0 4 ) n(1 \le n \le 10^4) n(1≤n≤104) 个元素的升序整型数组 n u m s nums nums 和一个值 t a r g e t target target,求实现一个函数查找 n u m s nums nums 中 t a r g e t target target 的下标,如果查找不到则返回 − 1 -1 −1。
- c++ 版本给出的基础框架代码如下,要求实现的是
search这个函数,数组参数传入的是一个vector<int>,是 STL 中常用的数组容器,支持动态扩容,vector的动态扩容有兴趣了解的,可以参考以下这篇文章:《C/C++ 面试 100 例》(四)vector 扩容策略。
class Solution {
public:
int search(vector<int>& nums, int target) {
}
};
a. 思路分析
- 1)令初始情况下,数组下标从 0 开始,且数组长度为 n n n,则定义一个区间,它的左端点是 l = 0 l=0 l=0,右端点是 r = n − 1 r = n-1 r=n−1;
- 2)生成一个区间中点 m i d = ( l + r ) / 2 mid = (l + r) / 2 mid=(l+r)/2,并且判断 m i d mid mid 对应的数组元素和给定的目标值的大小关系,主要有三种:
- 2.a)目标值 等于 数组元素,直接返回 m i d mid mid;
- 2.b)目标值 大于 数组元素,则代表目标值应该出现在区间 [ m i d + 1 , r ] [mid+1, r] [mid+1,r],迭代左区间端点: l = m i d + 1 l = mid + 1 l=mid+1;
- 2.c)目标值 小于 数组元素,则代表目标值应该出现在区间 [ l , m i d − 1 ] [l, mid-1] [l,mid−1],迭代右区间端点: r = m i d − 1 r = mid - 1 r=mid−1;
- 3)如果这时候 l > r l > r l>r,则说明没有找到目标值,返回 − 1 -1 −1;否则,回到 2)继续迭代。
b. 时间复杂度
- 由于每次都是将区间折半,所以二分查找的时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)。
c. 代码详解
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1; // (1)
while(l <= r) { // (2)
int mid = (l + r) >> 1; // (3)
if(nums[mid] == target) {
return mid; // (4)
}else if(target > nums[mid]) {
l = mid + 1; // (5)
}else if(target < nums[mid]) {
r = mid - 1; // (6)
}
}
return -1; // (7)
}
};
-
(
1
)
(1)
(1) 由于
vector的下标和数组一样是从 0 开始的,所以初始的左右查找区间端点为 0 和 数组长度减一,nums.size()返回的是数组的长度; - ( 2 ) (2) (2) 一直迭代左右区间的端点,直到 左端点 大于 右端点 结束;
-
(
3
)
(3)
(3)
>> 1等价于除 2,也就是这里mid代表的是l和r的中点; -
(
4
)
(4)
(4)
nums[mid] == target表示正好找到了这个数,则直接返回下标mid; -
(
5
)
(5)
(5)
target > nums[mid]表示target这个数在区间 [ m i d + 1 , r ] [mid+1, r] [mid+1,r] 中,所以才有左区间赋值如下:l = mid + 1; -
(
6
)
(6)
(6)
target < nums[mid]表示target这个数在区间 [ l , m i d − 1 ] [l, mid - 1] [l,mid−1] 中,所以才有右区间赋值如下:r = mid - 1; -
(
7
)
(7)
(7) 这一步呼应了
(
2
)
(2)
(2),表示这不到给定的数,直接返回
-1;
🥢5、双指针
- 接下来,以一个非常经典的面试题【最长不重复子串】为例,展开对双指针算法的讲解。
【例题5】给定一个长度为 n ( 1 ≤ n ≤ 1 0 7 ) n (1 \le n \le 10^7) n(1≤n≤107) 的字符串 s s s,求一个最长的满足所有字符不重复的子串。
a. 初步分析
- 首先我们分析一下这个问题的关键词,主要有以下几个:
- 1) n ≤ 1 0 7 n \le 10^7 n≤107;
- 2)最长;
- 3)所有字符不重复;
- 4)子串;
- 根据以上的几个关键词,我们可以得出一些结论。首先,根据 n n n 的范围已经能够大致确认这是一个需要 O ( n ) O(n) O(n) 或者 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) 的算法才能解决的问题;其次,“最长” 这个词告诉我们,可能是一个动态规划问题或者贪心问题,也有可能是搜索,所以这个关键词给我们的信息用处不大;而判断字符是否重复可以用 哈希表 在 O ( 1 ) O(1) O(1) 的时间内判断;最后,枚举所有 “子串” 的时间复杂度是 O ( n 2 ) O(n^2) O(n2) 的。
b. 朴素算法
- 由以上分析,我们可以发现第(1)个 和 第(4)个关键词给我们得出的结论是矛盾的,那么,我们可以先尝试减小 n n n 的范围,如果 n ≤ 1000 n \le 1000 n≤1000 时,怎么解决这个问题呢?
- 因为最后求的是满足条件的最长子串,所以我们如果能够枚举所有子串,那么选择长度最长的满足条件的子串就是答案了(这里的条件是指子串中所有字符都不同)。
用 a n s ans ans 记录我们需要求的最大不重复子串的长度,用一个哈希表 h h h 来代表某个字符是否出现过,算法描述如下:
1)枚举子串的左端点 i = 0 → n − 1 i = 0 \to n-1 i=0→n−1;
2)清空哈希表 h h h;
3)枚举子串的右端点 j = i → n − 1 j = i \to n-1 j=i→n−1,如果当前这个字符 s j s_j sj 出现过(即 h [ s j ] = t r u e h[s_j] = true h[sj]=true),则跳出 j j j 的循环;否则,令 h [ s j ] = t r u e h[s_j] = true h[sj]=true,并且用当前长度去更新 a n s ans ans(即 a n s = m a x ( a n s , j − i + 1 ) ans= max(ans, j - i +1) ans=max(ans,j−i+1));
4)回到 2);
- c++ 代码实现如下:
int getmaxlen(int n, char *str, int& l, int& r) {
int ans = 0, i, j, len;
memset(h, 0, sizeof(h));
for(i = 0; i < n; ++i) { // 1)
j = i;
memset(h, false, sizeof(h)); // 2)
while(j < n && !h[str[j]]) {
h[ str[j] ] = true; // 3)
len = j - i + 1;
if(len > ans)
ans = len, l = i, r = j;
++j;
}
}
return ans;
}
- 1)这一步枚举对应子串的左端点 i i i;
- 2)这一步用于清空哈希表 h h h,其中 h [ s j ] = t r u e h[ s_j ] = true h[sj]=true 代表原字符串的第 j j j 个字符 s j s_j sj 是否出现在以第 i i i 个字符为左端点的子串中;
- 3)而第三步可以这么理解:如果字符串 s [ i : j ] s[i:j] s[i:j] 中已经出现重复的字符,那么 s [ i : j + 1 ] , s [ i : j + 2 ] , . . . , s [ i : n − 1 ] s[i:j+1],s[i:j+2], ... , s[i:n-1] s[i:j+1],s[i:j+2],...,s[i:n−1] 必然会有重复字符,所以这里不需要继续往下枚举,直接跳出第二层循环即可。
- 这个算法执行完毕, a n s ans ans 就是我们要求的最长不重复子串的长度, [ l , r ] [l, r] [l,r] 代表了最长不重复子串在原字符串的区间。正确性毋庸置疑,因为已经枚举了所有子串的情况,如果字符集的个数 z z z,算法的时间复杂度就是 O ( n z ) O(nz) O(nz)。
- 最后奉上一张动图,代表了上述朴素算法的求解过程,如图所示:

- 字符串下标从 0 开始,最长无重复子串为: s [ 1 : 5 ] = b c a e d s[1:5] = bcaed s[1:5]=bcaed,长度为 5。
- 由于是字符串,字符集的个数 z z z 最多 256,所以时间复杂度基本就是 O ( 256 n ) O(256n) O(256n),当 n ≤ 1 0 7 n \le 10^7 n≤107 时,这个时间复杂度是无法接受的,需要想办法优化。
c. 优化算法
- 如果仔细思考上面朴素算法的求解过程,就会发现:枚举子串的时候有很多区间是重叠的,所以必然存在许多没有必要的重复计算。
- 我们考虑一个子串以
s
i
s_i
si 为左端点,
s
j
s_j
sj 为右端点,且
s
[
i
:
j
−
1
]
s[i:j-1]
s[i:j−1] 中不存在重复字符,
s
[
i
:
j
]
s[i:j]
s[i:j] 中存在重复字符(换言之,
s
j
s_j
sj 和
s
[
i
:
j
−
1
]
s[i:j-1]
s[i:j−1] 中某个字符相同)。如图所示:

- 那么我们没必要再去检测 s [ i : j + 1 ] s[i:j+1] s[i:j+1], s [ i : j + 2 ] s[i:j+2] s[i:j+2], s [ i : n − 1 ] s[i:n-1] s[i:n−1] 这几个字符串的合法性,因为当前情况 s [ i : j ] s[i:j] s[i:j] 是非法的,而这些字符串是完全包含 s [ i : j ] s[i:j] s[i:j] 的,所以它们必然也是不合法的。
- 那么我们可以把枚举的左端点自增,即: i = i + 1 i = i +1 i=i+1,这时,按照朴素算法的实现,右端点需要重置,即 j = i j = i j=i,实际上这里的右端点可以不动。
- 可以这么考虑,由于
s
j
s_j
sj 这个字符和
s
[
i
:
j
−
1
]
s[i:j-1]
s[i:j−1] 中的字符产生了重复,假设这个重复的字符的下标为
k
k
k,那么
i
i
i 必须满足
i
>
k
i \gt k
i>k,换言之,
i
i
i 可以一直自增,直到
i
=
k
+
1
i = k+1
i=k+1,如图所示:

- 利用上述思路,我们重新实现 最长不重复子串 的算法, c++ 代码实现如下:
int getmaxlen(int n, char *str, int& l, int& r) {
int ans = 0, i = 0, j = -1, len; // 1)
memset(h, 0, sizeof(h)); // 2)
while (j++ < n - 1) { // 3)
++h[ str[j] ]; // 4)
while (h[ str[j] ] > 1) { // 5)
--h[ str[i] ];
++i;
}
len = j - i + 1;
if(len > ans) // 6)
ans = len, l = i, r = j;
}
return ans;
}
- 1)初始化
i = 0, j = -1,代表 s [ i : j ] s[i:j] s[i:j] 为一个空串,从空串开始枚举; - 2)同样需要维护一个哈希表,哈希表记录的是当前枚举的区间 s [ i : j ] s[i:j] s[i:j] 中每个字符的个数;
- 3)只推进子串的右端点;
- 4)在哈希表中记录字符的个数;
- 5)当
h[ str[j] ] > 1满足时,代表出现了重复字符,这时候左端点 i i i 推进,直到没有重复字符为止; - 6)记录当前最优解
j-i+1; - 这个算法执行完毕,我们就可以得到最长不重复子串的长度为 a n s ans ans,并且 i i i 和 j j j 这两个指针分别只自增 n n n 次,两者自增相互独立,是一个相加而非相乘的关系,所以这个算法的时间复杂度为 O ( n ) O(n) O(n) 。
- 利用该优化算法优化后的最长不重复子串的求解过程如图所示:

- 参考这个图,一个比较通俗易懂的解释:当区间 [ i , j ] [i, j] [i,j] 中存在重复(红色)字符时,左指针 i i i 自增;否则,右指针 j j j 自增。
🍴6、差分法
- 差分法一般配合前缀和。
- 对于区间 [ l , r ] [l, r] [l,r] 内求满足数量的数,可以利用差分法分解问题;
- 假设
[
0
,
x
]
[0, x]
[0,x] 内的
g
o
o
d
n
u
m
b
e
r
good \ number
good number 数量为
g
x
g_x
gx,那么区间
[
l
,
r
]
[l, r]
[l,r] 内的数量就是
g
r
−
g
l
−
1
g_r - g_{l-1}
gr−gl−1;分别用同样的方法求出
g
r
g_r
gr 和
g
l
−
1
g_{l-1}
gl−1,再相减即可;
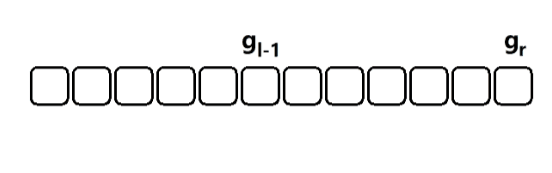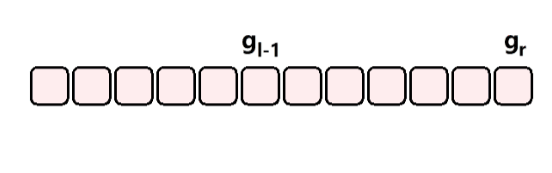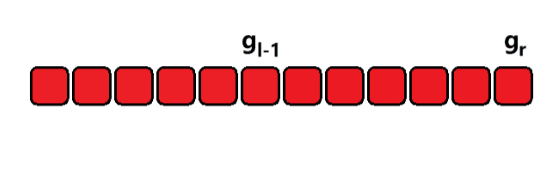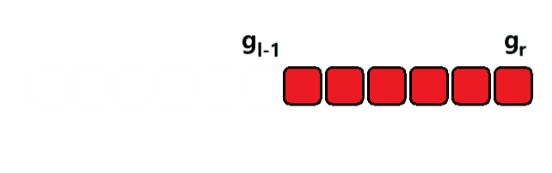
🅱7、位运算
- 位运算可以理解成对二进制数字上的每一个位进行操作的运算。
- 位运算分为 布尔位运算符 和 移位位运算符。
- 布尔位运算符又分为 位与(&)、位或(|)、异或(^)、按位取反(~);移位位运算符分为 左移(<<) 和 右移(>>)。
- 如图所示:

- 位运算的特点是语句短,但是可以干大事!
a、位与
【例题7】给出一个整数,现在要求将这个整数转换成二进制以后,将末尾连续的1都变成0,输出改变后的数(以十进制输出即可)。
- 我们知道,这个数的二进制表示形式一定是:
- . . . 0 11...11 ⏟ k ...0\underbrace{11...11}_{\rm k} ...0k 11...11
- 如果,我们把这个二进制数加上1,得到的就是:
- . . . 1 00...00 ⏟ k ...1\underbrace{00...00}_{\rm k} ...1k 00...00
- 我们把这两个数进行位与运算,得到:
- . . . 0 00...00 ⏟ k ...0\underbrace{00...00}_{\rm k} ...0k 00...00
- 所以,你学会了吗?代码如下:
x &= x - 1;
b、位或
【例题8】给定一个整数 x x x,将它低位连续的 0 都变成 1。
- 假设这个整数低位连续有 k k k 个零,二进制表示如下:
- . . . 1 00...00 ⏟ k ...1\underbrace{00...00}_{\rm k} ...1k 00...00
- 那么,如果我们对它进行减一操作,得到的二进制数就是:
- . . . 0 11...11 ⏟ k ...0\underbrace{11...11}_{\rm k} ...0k 11...11
- 我们发现,只要对这两个数进行位或,就能得到:
- . . . 1 11...11 ⏟ k ...1\underbrace{11...11}_{\rm k} ...1k 11...11
- 也正是题目所求,所以代码实现如下:
#include <stdio.h>
int main() {
int x;
scanf("%d", &x);
printf("%d\n", x | (x-1) ); // (1)
return 0;
}
-
(
1
)
(1)
(1)
x | (x-1)就是题目所求的 “低位连续零变一” 。
c、异或
【例题9】给定两个数 a a a 和 b b b,用异或运算交换它们的值。
- 这个是比较老的面试题了,直接给出代码:
#include <stdio.h>
int main() {
int a, b;
while (scanf("%d %d", &a, &b) != EOF) {
a = a ^ b; // (1)
b = a ^ b; // (2)
a = a ^ b; // (3)
printf("%d %d\n", a, b);
}
return 0;
}
- 我们直接来看
(
1
)
(1)
(1) 和
(
2
)
(2)
(2) 这两句话,相当于
b等于a ^ b ^ b,根据异或的几个性质,我们知道,这时候的b的值已经变成原先a的值了。 - 而再来看第
(
3
)
(3)
(3) 句话,相当于
a等于a ^ b ^ a,还是根据异或的几个性质,这时候,a的值已经变成了原先b的值。 - 从而实现了变量
a和b的交换。
d、左移
- 对于 x x x 模上一个 2 的次幂的数 y y y,我们可以转换成位与上 2 y − 1 2^y-1 2y−1。
- 即在数学上的:
- x m o d 2 y x \ mod \ 2^y x mod 2y
- 在计算机中就可以用一行代码表示:
x & ((1 << y) - 1)。
🧡8、贪心
- 贪心,一般就是按照当前最优解,去推算全局最优解。
- 所以,只有当当前最优解和全局最优解一致时才能用贪心算法。贪心算法的证明是比较难的,但是一些简单的贪心问题会比较直观,很容易看出来这个能够这么贪。
♈9、递归分治
- 分治,就是把问题分成若干子问题求解,子问题解决后,问题就解决了。一般利用递归实现。属于初学者比较头疼的内容。递归一开始学习的时候,一定要注意全局变量和局部变量的关系。
🙉饭不食,水不饮,题必须刷🙉
还不会C语言,和我一起打卡! 🌞《光天化日学C语言》🌞
LeetCode 太难?上简单题! 🧡《C语言入门100例》🧡
LeetCode 太简单?大神盘他! 🌌《夜深人静写算法》🌌
LeetCode 46. 全排列
【例题10】给定一个 不含重复数字 的长度小于 7 的数组 n u m s nums nums ,返回其 所有可能的全排列。
样例输入: n u m s = [ 1 , 2 , 3 ] nums = [1,2,3] nums=[1,2,3]
样例输出: [ [ 1 , 2 , 3 ] , [ 1 , 3 , 2 ] , [ 2 , 1 , 3 ] , [ 2 , 3 , 1 ] , [ 3 , 1 , 2 ] , [ 3 , 2 , 1 ] ] [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
a. 思路分析
- 全排列的种数是 n ! n! n!,这是最典型的深搜问题。我们可以把 n n n 个数两两建立无向边(即任意两个结点之间都有边,也就是一个 n n n 个结点的完全图),然后对每个点作为起点,分别做一次深度优先搜索,当所有点都已经标记时,输出当前的搜索路径,就是其中一个排列;
- 这里需要注意的是,回溯的时候需要将原先标记的点的标记取消,否则只能输出一个排列。
- 如下图,代表的是3个数的图表示:

- 3个数的全排列的深度优先搜索空间树如下图所示:

- 关于深度优先搜索的更深入内容,可以参考这篇文章:夜深人静写算法(一)- 搜索入门。
b. 时间复杂度
- 由于每次访问后会将标记过的节点标记回来,所以时间复杂度就是排列数,即 O ( n ! ) O(n!) O(n!)。
c. 代码详解
class Solution {
int hash[6];
void dfs(int dep, int maxdep, vector<int>& nums, vector<vector<int>>& ans, vector<int>& st) { // (1)
if(dep == maxdep) {
ans.push_back( st ); // (2)
return ;
}
for(int i = 0; i < maxdep; ++i) {
if(!hash[i]) { // (3)
hash[i] = 1;
st.push_back( nums[i] );
dfs(dep + 1, maxdep, nums, ans, st); // (4)
st.pop_back(); // (5)
hash[i] = 0; // (6)
}
}
}
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
memset(hash, 0, sizeof(hash));
vector<int> st;
dfs(0, nums.size(), nums, ans, st);
return ans;
}
};
-
(
1
)
(1)
(1)
dep代表本地递归访问第几个节点,maxdep代表递归的层数,vector<int>& nums则代表原始输入数组,vector<vector<int>>& ans代表结果数组,vector<int>& st代表存储当前搜索结果的栈; -
(
2
)
(2)
(2)
dep == maxdep代表一次全排列访问,这时候得到一个可行解,放入结果数组中; -
(
3
)
(3)
(3) 如果节点
i
i
i 未访问,则将第
i
i
i 个节点的值塞入搜索结果栈,并且用
hash数组标记已访问; - ( 4 ) (4) (4) 继续递归调用下一层;
- ( 5 ) (5) (5) 将栈顶元素弹出,代表本次访问的回溯;
- ( 6 ) (6) (6) 取消数组标记;
🚊10、简单动态规划
LeetCode 746. 使用最小花费爬楼梯
数组的每个下标作为一个阶梯,第 i i i 个阶梯对应着一个非负数的体力花费值 c o s t [ i ] cost[i] cost[i](下标从 0 开始)。每当爬上一个阶梯,都要花费对应的体力值,一旦支付了相应的体力值,就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时,可以选择从下标为 0 或 1 的元素作为初始阶梯。
样例输入: c o s t = [ 1 , 99 , 1 , 1 , 1 , 99 , 1 , 1 , 99 , 1 ] cost = [1, 99, 1, 1, 1, 99, 1, 1, 99, 1] cost=[1,99,1,1,1,99,1,1,99,1]
样例输出: 6 6 6
如图所以,蓝色的代表消耗为 1 的楼梯,红色的代表消耗 99 的楼梯。
a、思路分析
- 令走到第 i i i 层的最小消耗为 f [ i ] f[i] f[i]
- 假设当前的位置在 i i i 层楼梯,那么只可能从 i − 1 i-1 i−1 层过来,或者 i − 2 i-2 i−2 层过来;
- 如果从 i − 1 i-1 i−1 层过来,则需要消耗体力值: f [ i − 1 ] + c o s t [ i − 1 ] f[i-1] + cost[i-1] f[i−1]+cost[i−1];
- 如果从 i − 2 i-2 i−2 层过来,则需要消耗体力值: f [ i − 2 ] + c o s t [ i − 2 ] f[i-2] + cost[i-2] f[i−2]+cost[i−2];
- 起点可以在第 0 或者 第 1 层,于是有状态转移方程:
-
f
[
i
]
=
{
0
i
=
0
,
1
min
(
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
,
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
)
i
>
1
f[i] = \begin{cases} 0 & i=0,1\\ \min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\end{cases}
f[i]={0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])i=0,1i>1

b. 时间复杂度
- 状态数: O ( n ) O(n) O(n)
- 状态转移: O ( 1 ) O(1) O(1)
- 时间复杂度: O ( n ) O(n) O(n)
c. 代码详解
class Solution {
int f[1100]; // (1)
public:
int minCostClimbingStairs(vector<int>& cost) {
f[0] = 0, f[1] = 0; // (2)
for(int i = 2; i <= cost.size(); ++i) {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]); // (3)
}
return f[cost.size()];
}
};
-
(
1
)
(1)
(1) 用
f[i]代表到达第 i i i 层的消耗的最小体力值。 - ( 2 ) (2) (2) 初始化;
- ( 3 ) (3) (3) 状态转移;
有没有发现,这个问题和斐波那契数列很像,只不过斐波那契数列是求和,这里是求最小值。
6️⃣刷题顺序的建议
然后介绍一下刷题顺序的问题,我们刷题的时候千万不要想着一步到位,一开始,没有刷满三百题,姿态放低,都把自己当成小白来处理。
这里以刷 LeetCode 为例,我目前只刷了不到 50 题,所以我是小白。
当我是小白时,我只刷入门题,也就是下面这几个专题。先把上面所有的题目刷完,在考虑下一步要做什么。
👨👦1、入门算法
| 种类 | 链接 |
|---|---|
| 算法 | 算法入门 |
| 数据结构 | 数据结构入门 |
| 数组字符串专题 | 数组和字符串 |
| 动态规划专题 | 动态规划入门、DP路径问题 |
当入门的题刷完了,并且都能讲述出来自己刷题的过程以后,我们再来看初级的一些算法和简单的数据结构,简单的数据结构就是线性表了,包含:数组、字符串、链表、栈、队列 等等,即下面这些专题。
👩👧👦2、初级算法
| 种类 | 链接 |
|---|---|
| 算法 | 初级算法 |
| 栈和队列专题 | 队列 & 栈 |
上面的题刷完以后,其实已经算是基本入门了,然后就可以开始系统性的学习了。
当然,基本如果真的到了这一步,说明你的确已经爱上了刷题了,那么我们可以尝试挑战一下 LeetCode 上的一些热门题,毕竟热门题才是现在面试的主流,能够有更好的结果,这样刷题的时候也会有更加强劲的动力不是吗!
👩👩👧👦3、中级算法
| 种类 | 链接 |
|---|---|
| 算法 | 中极算法 |
| 二叉树专题 | 二叉树 |
| 热门题 | 热门题 TOP 100 |
7️⃣系统学习算法和数据结构
🚍1、进阶动态规划
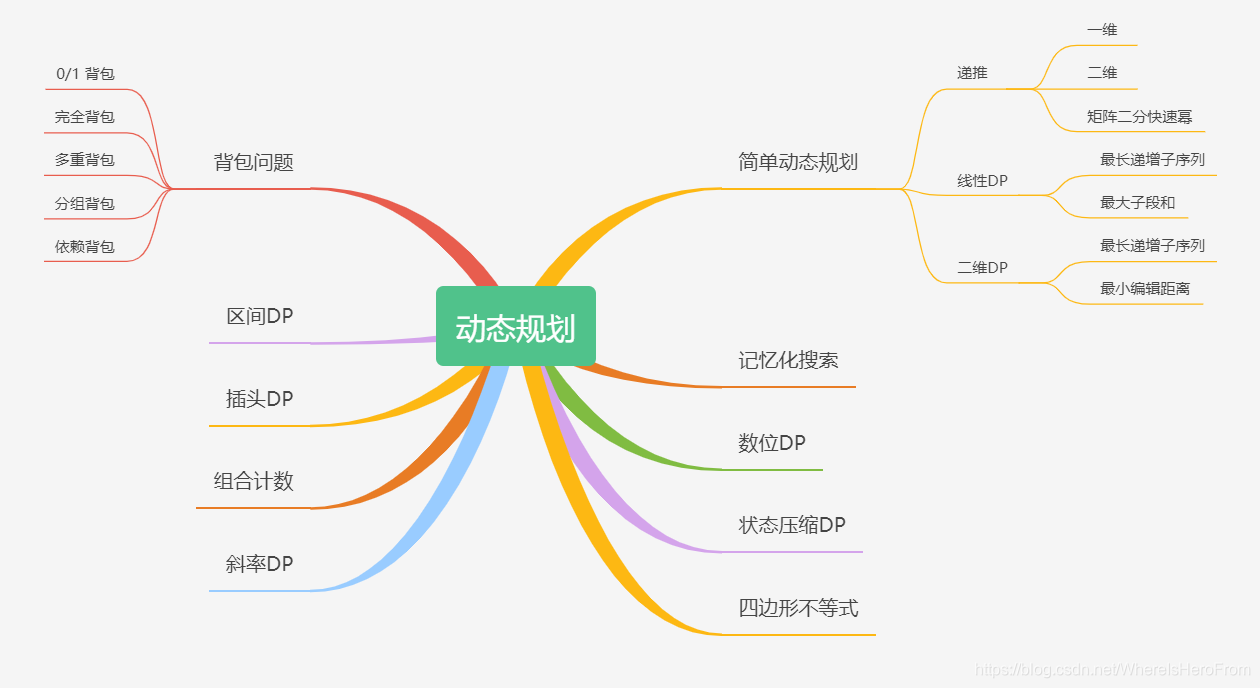
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(二)- 动态规划入门 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十六)- 记忆化搜索 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(十九)- 背包总览 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十)- 最长单调子序列 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十一)- 最长公共子序列 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十二)- 最小编辑距离 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十四)- 0/1 背包 | ★☆☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十五)- 完全背包 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十六)- 多重背包 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(二十七)- 区间DP | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(二十九)- 数位DP | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(十七)- 分组背包 | ★★★☆☆ | ★★★☆☆ |
| 夜深人静写算法(十八)- 依赖背包 | ★★★★☆ | ★★☆☆☆ |
| 夜深人静写算法(六)- RMQ | ★★★☆☆ | ★★☆☆☆ |
| 树形DP | 待更新 | … |
| 组合博弈 | 待更新 | … |
| 组合计数DP | 待更新 | … |
| 四边形不等式 | 待更新 | … |
| 状态压缩DP/TSP | 待更新 | … |
| 斜率优化的动态规划 | 待更新 | … |
| 插头DP | 待更新 | … |
🪐2、强劲图论搜索
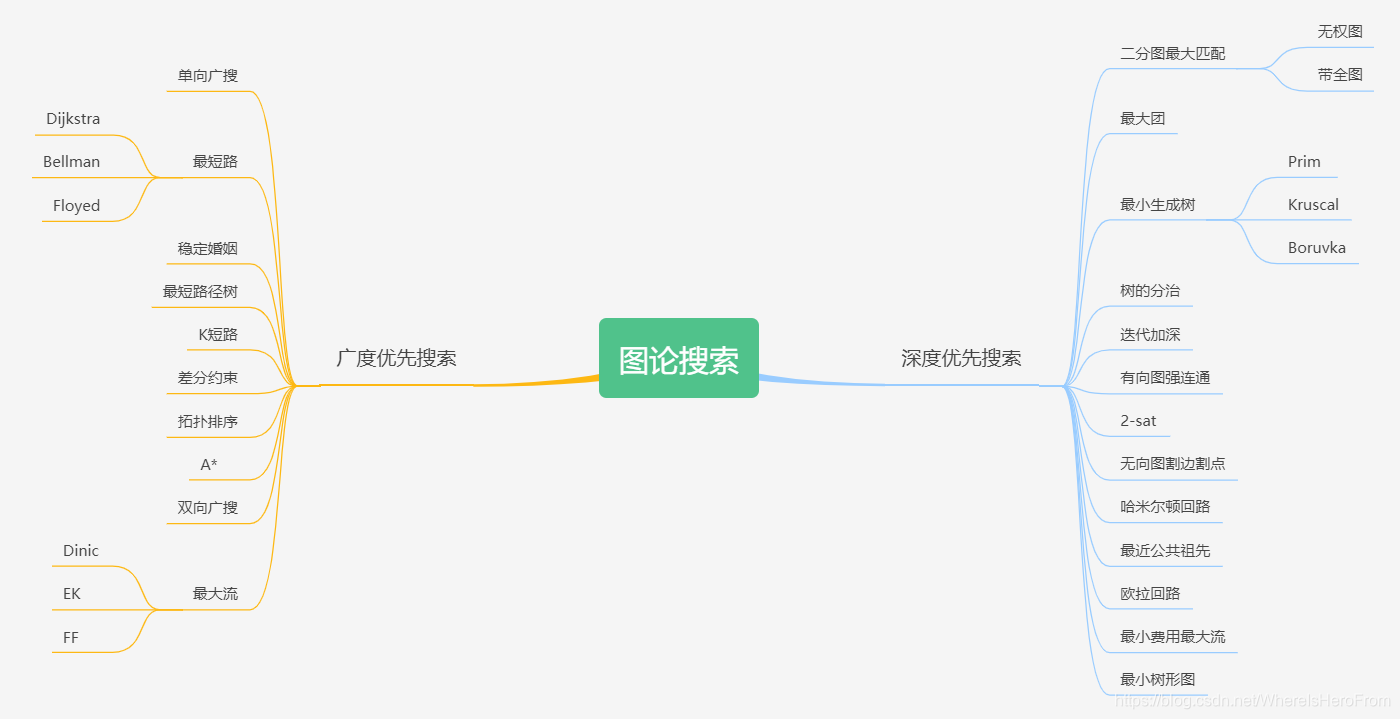
1、深度优先搜索
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(一)- 搜索入门 | ★☆☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(八)- 二分图最大匹配 | ★★☆☆☆ | ★★☆☆☆ |
| 最大团 | 待更新 | … |
| 最小生成树 | 待更新 | … |
| 树的分治 | 待更新 | … |
| 迭代加深 IDA* | 待更新 | … |
| 有向图强连通分量和2-sat | 待更新 | … |
| 无向图割边割点 | 待更新 | … |
| 带权图的二分图匹配 | 待更新 | … |
| 哈密尔顿回路 | 待更新 | … |
| 最近公共祖先 | 待更新 | … |
| 欧拉回路圈套圈 | 待更新 | … |
| 最小费用最大流 | 待更新 | … |
| 最小树形图 | 待更新 | … |
2、广度优先搜索
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(十)- 单向广搜 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(二十三)- 最短路 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(二十五)- 稳定婚姻 | ★★☆☆☆ | ★★☆☆☆ |
| 夜深人静写算法(二十四)- 最短路径树 | ★★★☆☆ | ★☆☆☆☆ |
| K 短路 | 待更新 | … |
| 差分约束 | 待更新 | … |
| 拓扑排序 | 待更新 | … |
| A* | 待更新 | … |
| 双向广搜 | 待更新 | … |
| 最大流 最小割 | 待更新 | … |
0️⃣3、进阶初等数论

| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(三)- 初等数论入门 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(三十)- 二分快速幂 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(三十一)- 欧拉函数 | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(三十二)- 费马小定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十三)- 扩展欧拉定理 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(三十四)- 逆元 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(三十五)- RSA 加密解密 | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(三十六)- 中国剩余定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十七)- 威尔逊定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十八)- 整数分块 | ★★☆☆☆ | ★★★★☆ |
| 卢卡斯定理 | 待更新 | … |
| 狄利克雷卷积 | 待更新 | … |
| 莫比乌斯反演 | 待更新 | … |
| 容斥原理 | 待更新 | … |
| 拉宾米勒 | 待更新 | … |
| Pollard rho | 待更新 | … |
| 莫队 | 待更新 | … |
| 原根 | 待更新 | … |
| 大步小步算法 | 待更新 | … |
| 二次剩余 | 待更新 | … |
| 矩阵二分快速幂 | 待更新 | … |
| Polya环形计数 | 待更新 | … |
🛑4、进阶计算几何
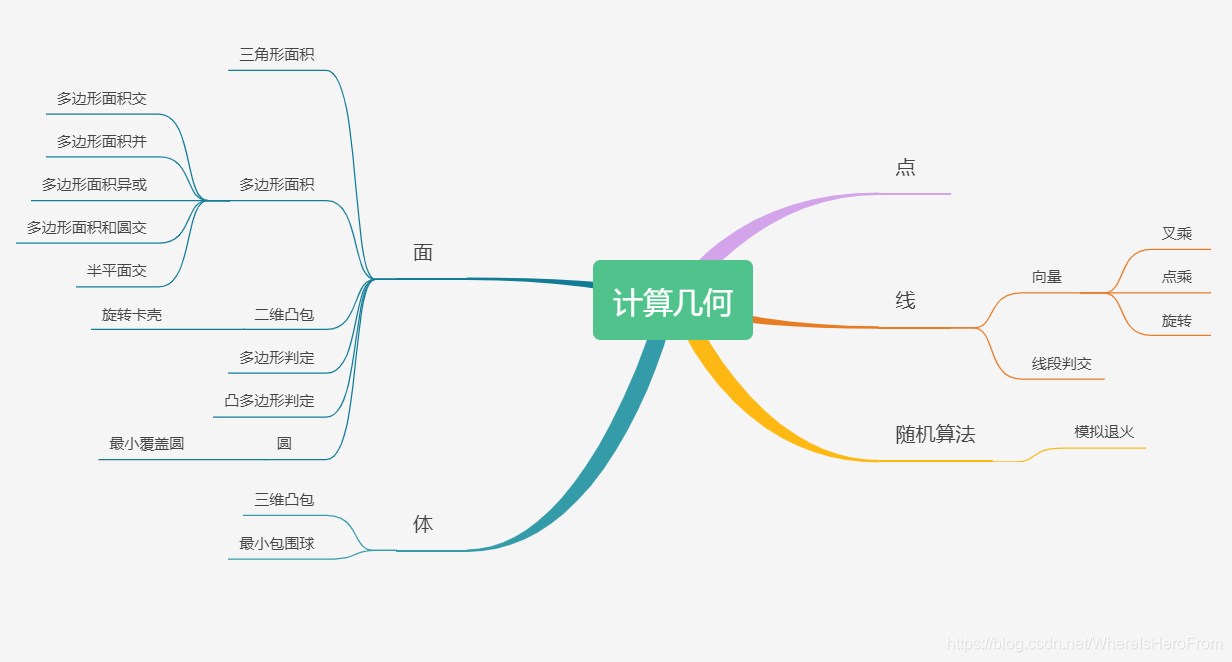
📏5、字符串的匹配
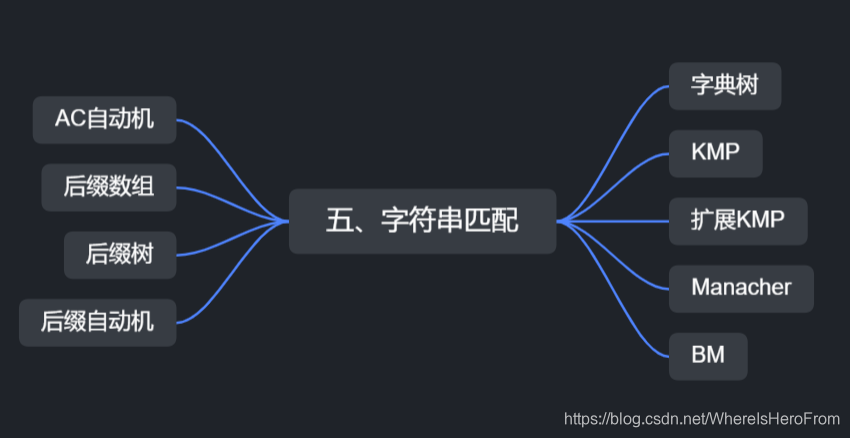
🎄6、高級数据结构
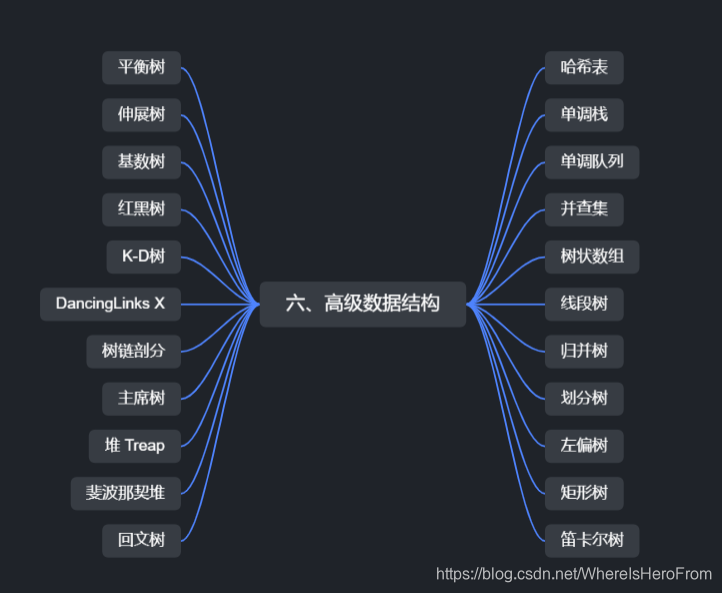
🙉饭不食,水不饮,题必须刷🙉
还不会C语言,和我一起打卡! 🌞《光天化日学C语言》🌞
LeetCode 太难?上简单题! 🧡《C语言入门100例》🧡
LeetCode 太简单?大神盘他! 🌌《夜深人静写算法》🌌



