推荐算法--协同过滤--小白理解_hcxddd的博客

一.协同过滤是什么？
协同过滤，英文又称Collaborative Filtering，简称CF，注意这里不是指游戏cf。
举个例子，你想和女朋友出去看场电影，但是你们两个都不知道看什么好，这个时候，你就会想，要不我问问身边和我兴趣差不多的伙伴有什么值得看的吧？这就是协同过滤的核心思想，即协同过滤是一种基于一组兴趣相同的用户或项目进行的推荐。
算法优点：
①协同推荐是应用最广泛的推荐算法，可以过滤掉许多人难以量化描述的概念标签的构建；
②仅使用用户行为的进行推荐，极大的提升了速度与准确度；
③可以很好地发现用户的潜在兴趣偏好。
算法缺点
①用户对商品的评价非常稀疏，而有些用户对使用过的商品根本不做评价，这样基于用户的评价所得到的用户间的相似性可能不准确；
②随着用户和物品的增多，系统的性能会越来越低，甚至会出现内存耗尽；
③对于新用户或者新物品，推荐的质量会较差，即常说的冷启动问题。

二.相似度的计算
在相似度的计算中，使用sim来代替英文similarity（相似度），用sim（a,b）来表示a与b的相似度。下面为3个关于相似度的经典算法。
1.余弦相似度：2.1 余弦定理相似性度量余弦距离通过向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。三角形余弦定理公式： c o s A = b 2 + c 2 − a 2 2 b c cosA=\frac{b^{2}+c^{2}-a^{2}}{2bc} cosA=2bcb2+c2−a2​由三角形余弦定理公式可知，角 A 越小，bc 两边越接近。当 A 为 0 度时，bc 两边完全重合。在向量空间中，对于向量 a 和向量 b 符合公式： c o s C = < a ⃗ , b ⃗ > ∣ a ⃗ ∣ ∣ b ⃗ ∣ cosC=\frac{<\vec a,\vec b>}{|\vec a||\vec b|} cosC=∣a ∣∣b ∣<a ,b >​当 a 和 b 越接近（越相似）时，余弦值就越大，最大为 1.所以在比对 a 和 b 的相似度时，可以将其向量化后，计算它的余弦值，从而比较其相似度。即： s i m ( a , b ) = c o s ( a ⃗ b ⃗ ) = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ sim(a,b)=cos(\vec a\vec b)=\frac{\vec a·\vec b}{|\vec a|·|\vec b|} sim(a,b)=cos(a b )=∣a ∣⋅∣b ∣a ⋅b ​类似的也可以推广到多个样本的相似性度量公式： s i m ( a , b , ⋅ ⋅ ⋅ ) = c o s θ = x 1 y 1 + x 2 y 2 + ⋅ ⋅ ⋅ + x n y n x 1 2 + x 2 2 + ⋅ ⋅ ⋅ + x n 2 ⋅ y 1 2 + y 2 2 + ⋅ ⋅ ⋅ + y n 2 sim(a,b,···)=cosθ=\frac{x_{1}y_{1}+x_{2}y_{2}+···+x_{n}y_{n}}{\sqrt{x_{1}^{2}+x_{2}^{2}+···+x_{n}^{2}}·\sqrt{y_{1}^{2}+y_{2} ^{2}+···+y_{n}^{2}}} sim(a,b,⋅⋅⋅)=cosθ=x12​+x22​+⋅⋅⋅+xn2​ ​⋅y12​+y22​+⋅⋅⋅+yn2​ ​x1​y1​+x2​y2​+⋅⋅⋅+xn​yn​​对于集合 A 和集合 B 的相似性度量，为了方便计算，我们往往会用到下面的公式（计算的结果大小和上面的公式计算的结果是一样的）： s i m ( A , B ) = A ∩ B ∣ A ∣ ⋅ ∣ B ∣ sim(A,B)=\frac{A∩B}{\sqrt{|A|·|B|}} sim(A,B)=∣A∣⋅∣B∣ ​A∩B​

2.欧几里得距离（euclidea nmetric）（也称欧式距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
那距离是如何反映出相似度的呢，很简单，我们总是希望相似度越大返回的值越大。所以我们取距离的倒数即可（因为距离越大相似度越小），又因为分母不能为0，所以我们往往取函数值加1的倒数。

3：皮尔逊相关度
皮尔逊相关系数是一种度量两个变量间相关程度的方法。它是一个介于 1 和 -1 之间的值，其中，1 表示变量完全正相关， 0 表示无关，-1 表示完全负相关。公式有很多，这里取其中一个我认为最好理解的。

相关系数：一般指两个事物（在函数里经常说变量）之间的关系程度。
如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

(1)、当相关系数为0时，X和Y两变量无关系。
(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：
相关系数：
0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关

三.
1.基于物品（ItemCF）的协同过滤：

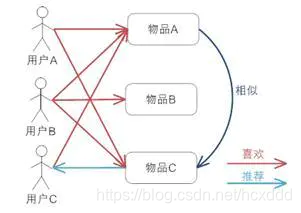
基本原理：通过某个用户的浏览记录，来分析用户对于某类物品的偏好程度，从而为用户推荐相似的物品。即相似的物品可能会被同一用户喜欢。

算法过程实现：
1.建立 物品 — 用户 倒排表；
物品 a：用户 A、用户 B、用户 C
物品 b：用户 C
物品 c：用户 A、用户 B
2.计算各物品之间的相似度(使用余弦定理相似性度量）；可以构建如下的相似度矩阵：

3.根据物品的相似度和用户的历史记录给用户生成推荐列表

通过如下公式计算用户 u 对一个物品 j 的购买预测值：
p ( u , j ) = ∑ i ∈ N ( u ) ∩ S ( i , k ) w j i r u i p(u,j)=\sum_{i∈N(u)∩S(i,k)}w_{ji}r_{ui} p(u,j)=∑i∈N(u)∩S(i,k)​wji​rui​
其中， p ( u , j ) p(u,j) p(u,j) 表示用户 u u u 对物品 j j j 的兴趣， N ( u ) N(u) N(u) 表示用户喜欢的物品集合（ i i i 是该用户喜欢的某一个物品）， S ( i , k ) S(i,k) S(i,k) 表示和物品 i i i 最相似的 K K K 个物品集合（ j j j 是这个集合中的某一个物品）， w j i w_{ji} wji​ 表示物品 j 和物品 i 的相似度， r u i r_{ui} rui​ 表示用户 u u u 对物品 i i i 的兴趣（这里简化 r u i r_{ui} rui​ 都等于 1）。
例如：我们默认K等于1, p ( C , c ) = 2 6 p(C,c)=\frac{2}{\sqrt{6}} p(C,c)=6 ​2​， p ( B , b ) = 1 3 p(B,b)=\frac{1}{\sqrt{3}} p(B,b)=3 ​1​

4.向用户展示推荐物品

**代码实现：**
import numpy as np
from math import sqrt
'''
用户/物品 | 物品a | 物品b | 物品c 
用户A    |   √    |          |   √
用户B    |   √    |          |   √
用户C    |   √    |   √     |
'''
#定义余弦相似性度量计算
def cosine(ls_1,ls_2,m): #ls_1,ls_2表示用户1,2的相关数组，m表示总的物品数
    Numerator = 0 #公式中的分子
    abs_1 = abs_2 = 0 #分母中两向量的绝对值,即代表模
    for i in range(m):
        Numerator += ls_1[i] * ls_2[i]#同时喜欢才加一，就算一个人喜欢，另一个人不喜欢，相乘仍为零
        if ls_1[i] == 1:
            abs_1 += ls_1[i]#喜欢就加一
        if ls_2[i] == 1:
            abs_2 += ls_2[i]#喜欢就加一
    Denominator = sqrt(abs_1 * abs_2) #公式中的分母
    return Numerator/Denominator
    
#定义预测函数
def predict(w_uv,r_vi=1):
    p = w_uv * r_vi
    return p
    
if __name__ == "__main__":#一些牛b的代码都会有
    #建立用户 - 物品矩阵
    user_item = np.array([[1,0,1],
                        [1,0,1],
                        [1,1,0]])
    print("用户-物品矩阵：")
    print(user_item)#打印用户-物品矩阵
    user = ['用户A','用户B','用户C']
    item = ['物品a','物品b','物品c']
    n = len(user) #n 个用户
    m = len(item) #m 个物品
    K = 1 #只找到一个最相似物品
    
    
    #建立物品 - 用户倒排表
    item_user = user_item.T
    print("物品-用户矩阵：")
    print(item_user)
    
    #构建物品 - 物品相似度矩阵
    sim = np.zeros((n,n)) #相似度矩阵，默认全为 0
    for i in range(n): 
        for j in range(n):
            if i < j:
                sim[i][j] = cosine(item_user[i],item_user[j],m)#用到了前面定义的函数
                sim[j][i] = sim[i][j]#代表用户顺序不同但相似度一样
    print("得到的物品-物品相似度矩阵：")
    print(sim) #打印物品 - 物品相似度矩阵
    
    #推荐物品
    max_sim = [0,0,0] #存放每个物品的相似物品
    r_list = [[],[],[]] #存放推荐给每个用户的物品
    p = [[],[],[]] #每个用户被推荐物品的预测值列表
    for i in range(m): #m 个物品循环 m 次
        #找到与物品 i 最相似的物品
        for j in range(len(sim[i])): #range () 里面写 m 也可以，二者等同
            if max(sim[i]) != 0 and sim[i][j] == max(sim[i]):#max代表最大值
                max_sim[i] = item[j] #此时的 j 就是相似物品的编号
                break #break 目的：一是结束当前循环，二是当前的 j 后面有用
        if max_sim[i] == 0:
            continue #等于 0，表明当前物品无相似物品，继续下个物品
        #找出应该推荐的物品，并计算预测值
        for k in range(K): #为了更契合预测值计算公式，因为这里 K=1，所以也可以省去这个 for
            for x in range(n): #n 个用户循环 n 次
                if item_user[i][x] == 1 and item_user[j][x] == 0:#当前物品用户知道，而相似物品该用户不知道
                    r_list[x].append(max_sim[i])
                    p[x].append(predict(sim[i][j])) 
    
    #打印结果
    for i in range(n): #n 个用户循环 n 次
        if len(r_list[i]) > 0: #当前用户有被推荐的物品
            print("向{:}推荐的物品有：".format(user[i]),end='')#end的作用是防止光标移动到下一行
            print(r_list[i])
            print("该用户对以上物品该兴趣的预测值为：",end='')
            print(p[i])
        print()#输出一行空白，即换行

**输出结果：**
用户-物品矩阵：
[[1 0 1]
 [1 0 1]
 [1 1 0]]
物品-用户矩阵：
[[1 1 1]
 [0 0 1]
 [1 1 0]]
得到的物品-物品相似度矩阵：
[[0.         0.57735027 0.81649658]
 [0.57735027 0.         0.        ]
 [0.81649658 0.         0.        ]]


向用户C推荐的物品有：['物品c']
该用户对以上物品该兴趣的预测值为：[0.8164965809277261]

2.基于用户的(userCF）的协同过滤：
基本原理：通过寻找与当前查询者口味或偏好类似的用户，将他们的一些喜好物品推荐给当前查询者。即相似的用户会喜欢相同的物品

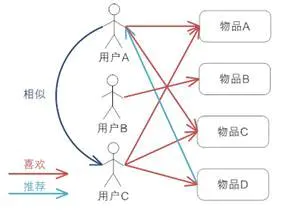
由图片我们可以观察出来，用户A与用户C的偏好类似，而用户C又在喜欢物品A和B的基础上喜欢物品C，所以我们考虑将物品C推荐给用户A。

算法过程实现：
1.计算各个用户之间的相似度（使用余弦定理相似性度量）；可以构建如下的相似度矩阵：

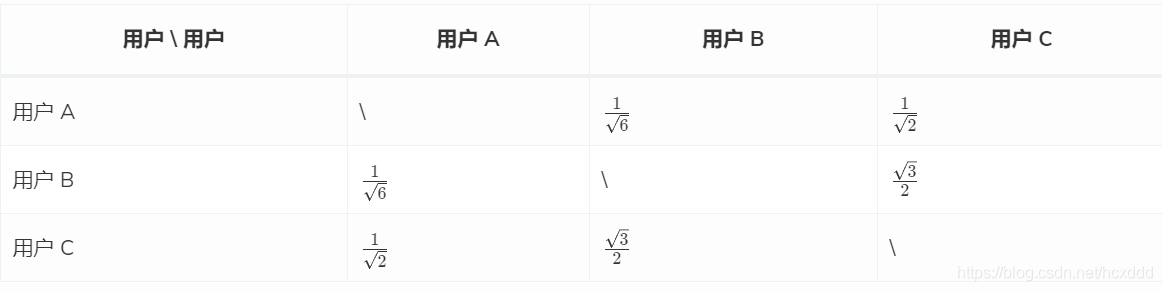
2.根据相似度的高低找到各用户的相似用户；
用户 A 的相似用户为用户 C；
用户 B 的相似用户为用户 C；
用户 C 的相似用户为用户 B。

3.找到相似用户购买过而目标用户不知道的物品，计算目标用户对这样的物品感兴趣的预测值（就是预测目标用户购买的可能性），向目标用户推荐这些物品。

通过如下公式计算用户 u 对一个物品 i的购买预测值： p ( u , i ) = ∑ i ∈ N ( v ) ∩ S ( u , k ) w u v r v i p(u,i)=\sum_{i∈N(v)∩S(u,k)}w_{uv}r_{vi} p(u,i)=i∈N(v)∩S(u,k)∑​wuv​rvi​其中， p ( u , j ) p(u,j) p(u,j) 表示用户 u u u 对物品 j j j 的兴趣， N ( v ) N(v) N(v) 表示用户喜欢的物品集合（ i i i 是该用户喜欢的某一个物品）， S ( u , k ) S(u,k) S(u,k) 表示和用户 u u u 最相似的 K K K 个用户集合（ u u u 是这个集合中的某一个用户）， w u v w_{uv} wuv​ 表示用户u 和用户v的相似度， r v i r_{vi} rvi​ 表示用户 v v v 对物品 i i i 的兴趣（这里简化 r v i r_{vi} rvi​ 都等于 1）。
例如：我们默认 K = 1 K=1 K=1， p ( A , b ) = 1 2 p(A,b)=\frac{1}{\sqrt{2}} p(A,b)=2 ​1​， p ( B , c ) = 3 2 p(B,c)=\frac{\sqrt{3}}{2}\qquad p(B,c)=23 ​​

4.向用户展示推荐物品。

**代码实现：**
import numpy as np
from math import sqrt
'''
用户/物品 | 物品a | 物品b | 物品c | 物品d
用户A     |   √  |       |   √   | 
用户B     |   √  |   √   |       |   √
用户C     |   √  |   √   |   √   |   √ 
'''
#定义余弦相似性度量计算
def cosine(ls_1,ls_2,m):#ls_1,ls_2表示用户1,2的相关数组，m表示总的物品数
    Numerator = 0 #公式中的分子
    abs_1 = abs_2 = 0 #分母中两向量的绝对值，即代表模
    for i in range(m):
        Numerator += ls_1[i] * ls_2[i]#同时喜欢才加一，就算一个人喜欢，另一个人不喜欢，相乘仍为零
        if ls_1[i] == 1:
            abs_1 += ls_1[i]#喜欢就加一
        if ls_2[i] == 1:
            abs_2 += ls_2[i]#喜欢就加一
    Denominator = sqrt(abs_1 * abs_2) #公式中的分母
    return Numerator/Denominator
    
#定义预测函数
def predict(w_uv,r_vi=1):
    p = w_uv * r_vi
    return p
    
if __name__ == "__main__":
    #建立用户 - 物品矩阵
    user_item = np.array([[1,0,1,0],
                        [1,1,0,1],
                        [1,1,1,1]])
    print("用户-物品矩阵：")
    print(user_item)
    user = ['用户A','用户B','用户C']
    item = ['物品a','物品b','物品c','物品d']
    n = len(user) #n 个用户
    m = len(item) #m 个物品
    K = 1 #只找到一个最相似用户
    
    #构建用户 - 用户相似度矩阵
    sim = np.zeros((n,n)) #相似度矩阵，默认全为 0
    for i in range(n): 
        for j in range(n):
            if i < j:
                sim[i][j] = cosine(user_item[i],user_item[j],m)#用到了前面定义的函数
                sim[j][i] = sim[i][j]#代表用户顺序不同但相似度一样
    print("得到的用户-用户相似度矩阵：")
    print(sim) #打印用户 - 用户相似度矩阵
    # 推荐物品
    max_sim = [0, 0, 0]  # 存放每个用户的相似用户
    r_list = [[], [], []]  # 存放推荐给每个用户的物品
    p = [[], [], []]  # 每个用户被推荐物品的预测值列表
    for i in range(n):  # n 个用户循环 n 次
        # 找到与用户 i 最相似的用户
        for j in range(len(sim[i])):  # range () 里面写 n 也可以，二者等同
            if max(sim[i]) != 0 and sim[i][j] == max(sim[i]):#max代表最大值
                max_sim[i] = user[j]  # 此时的 j 就是相似用户的编号
                break  # break 目的：一是结束当前循环，二是当前的 j 后面有用
        if max_sim[i] == 0:
            continue  # 等于 0，表明当前用户无相似用户，无需推荐，继续下个用户

        # 找出应该推荐的物品，并计算预测值
        for k in range(K):  # 为了更契合预测值计算公式，因为这里 K=1，所以也可以省去这个 for
            for x in range(m):  # m 个物品循环 m 次
                if user_item[i][x] == 0 and user_item[j][x] == 1:  # 目标用户不知道，而相似用户知道
                    r_list[i].append(item[x])
                    p[i].append(predict(sim[i][j]))

                    # 打印结果
    for i in range(n):  # n 个用户循环 n 次
        if len(r_list[i]) > 0:  # 当前用户有被推荐的物品
            print("向{:}推荐的物品有：".format(user[i]), end='')#end的作用是防止光标移动到下一行
            print(r_list[i])
            print("该用户对以上物品该兴趣的预测值为：", end='')
            print(p[i])
        print()#输出一行，即换行

**输出结果：**
用户-物品矩阵：
[[1 0 1 0]
 [1 1 0 1]
 [1 1 1 1]]
得到的用户-用户相似度矩阵：
[[0.         0.40824829 0.70710678]
 [0.40824829 0.         0.8660254 ]
 [0.70710678 0.8660254  0.        ]]
向用户A推荐的物品有：['物品b', '物品d']
该用户对以上物品该兴趣的预测值为：[0.7071067811865475, 0.7071067811865475]

向用户B推荐的物品有：['物品c']
该用户对以上物品该兴趣的预测值为：[0.8660254037844387]

四.UserCF和ItemCF的比较
Item CF是利用物品间的相似性来推荐的，所以假如用户的数量远远超过物品的数量，那么可以考虑使用Item CF，比如购物网站，因其物品的数据相对稳定，因此计算物品的相似度时不但计算量较小，而且不必频繁更新;
User CF更适合做新闻、博客或者微内容的推荐系统，因为其内容更新频率非常高，特别是在社交网络中，User CF是一个更好的选择，可以增加用户对推荐解释的信服程度。
总结：即如果人流量太大，考虑ItemCF，可以减少计算量；如果物流量太大，考虑UserCF，同样也是减少了计算量。

五.人工智能实践过程分为三个步骤：数据，学习与决策。
因此，有了评分矩阵后，我们便可以预测决策了。
例如：某个用户喜欢图书1，那我们怎么才能知道该不该向他推荐图书二或其他书呢？这里我介绍两种方法：
一.根据相似度预测评分来推荐物品


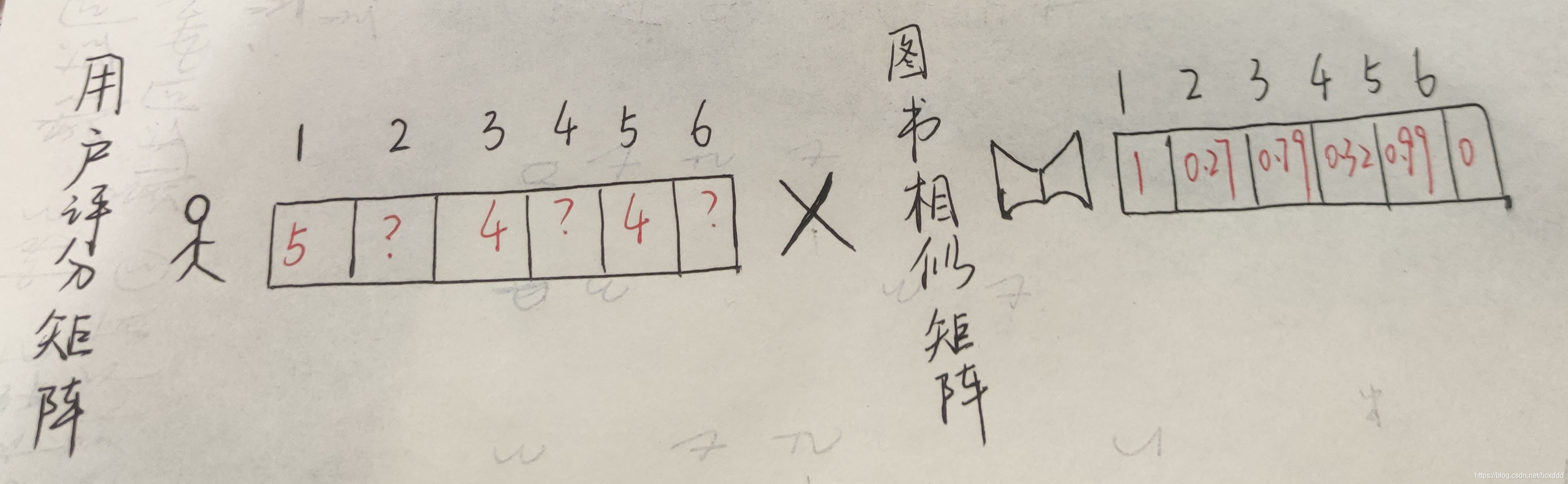
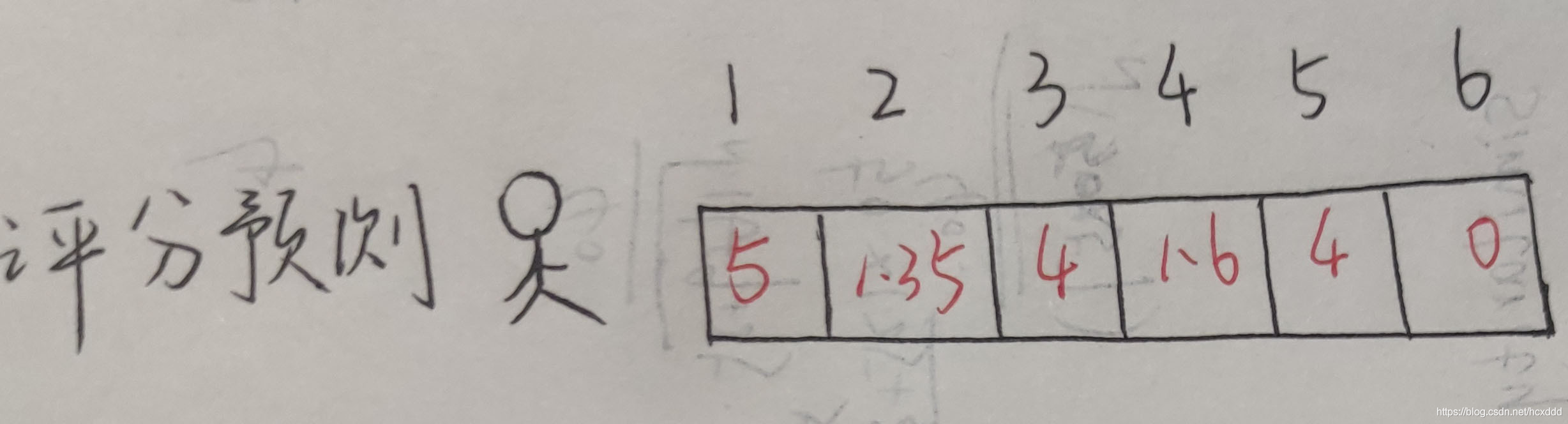
即通过将用户评分矩阵与图书相似矩阵进行乘积来获得最后的评分预测，评分越高，推荐的可信度就越大；同理，评分越低，推荐的可信度就越小。

二.根据相似度排序推荐物品

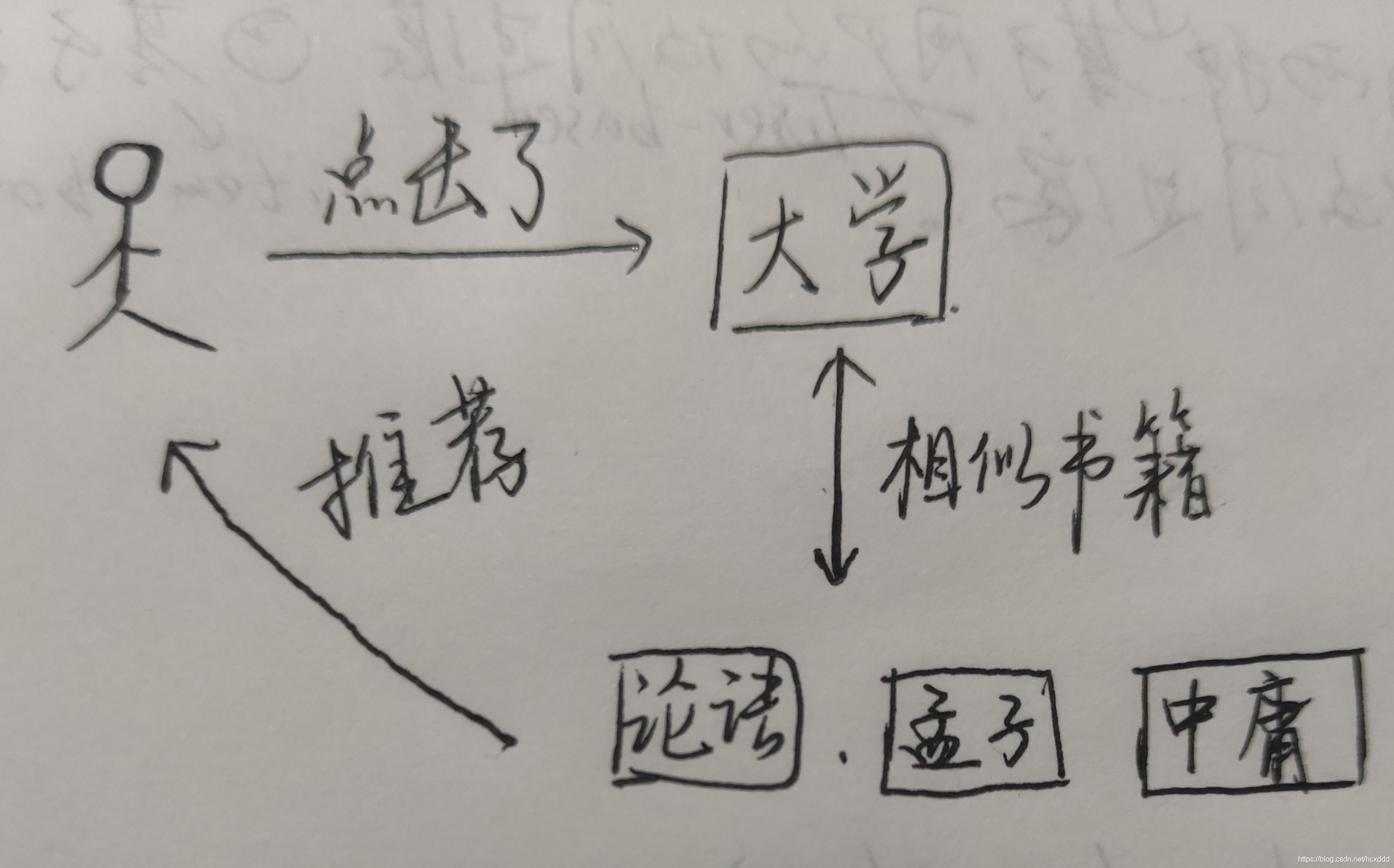
即用户看了大学这本书，然后我们发现与其类似的论语等书，便可根据相似度向用户推荐。

补充：