一、为什么要引入AM
引入 AM(幅度调制)调制与解调 是为了在通信系统中有效地传输信号。大部分原始信号(如语音、音频等)的频率范围较低,直接传输这些低频信号会受到传输距离和质量的限制。通过调制,将低频信号的频率迁移到较高的载波频率上,而高频信号对干扰的抗性通常更强,因为许多自然噪声源的频率范围较低。
二、AM调制与解调的原理
1.AM调制原理
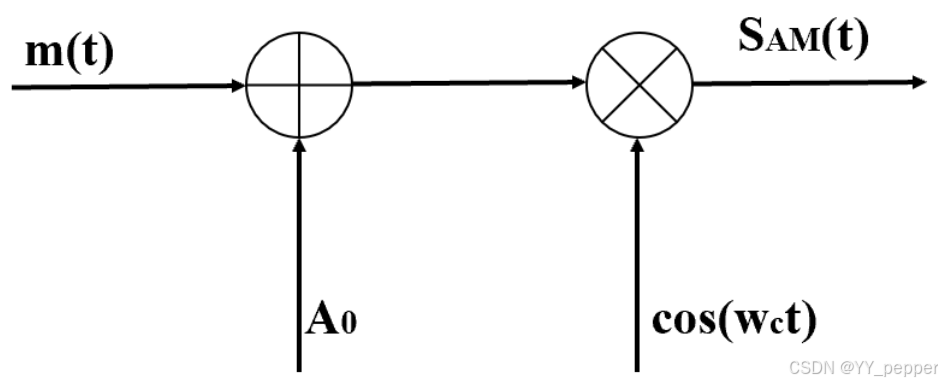
基带信号m(t)与直流分量A0相加,然后和高频载波相乘实现AM信号的调制。
2.AM解调原理
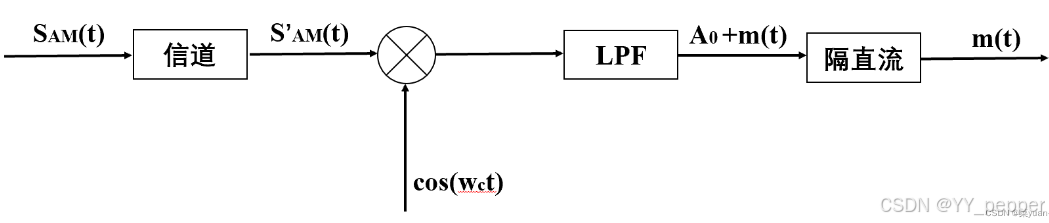
AM信号经信道传输,引入噪声后,得到Sam'(t),再和载波相乘,经过低通滤波器,隔直流后会付出原始基带信号。
三、 matlab代码实现
1.AM.m文件,主文件
%AM调制过程clc;close all;%% 基本参数fm = 100; %基带信号频率T = 2; %信号持续2sfs = 20000; %采样频率,满足奈奎斯特定理即可; %这里取20倍为了绘制更多的细节,让时域信号更平滑dt = 1/fs; %采样间隔N = T/dt; %采样点数t = 0:dt:dt*N-dt; %横坐标时间轴%% *****************调制信号的时域波形*****************Am = 1; %调制信号幅值mt = Am*cos(2*pi*fm*t); %调制信号figure(1); %创建一个新图形subplot(3,2,1); %创建3×2的子图集合,并在第一个位置显示plot(t,mt,'Linewidth',1); %绘图,线条宽度为1xlabel('t/时间'); %必须放在plot后面ylabel('调制信号m(t)');title('调制信号时域波形');axis([0,0.1,-1.1,1.1]); %横纵坐标范围[xmin,xmax,ymin,ymax]%% *****************调制信号的频域波形*****************[f,mf] = T2F(t,mt); %傅里叶变换,调用T2F函数,并返回f、mf的值subplot(3,2,2);plot(f,abs(mf),'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度/m(f)');title('调制信号的频谱');axis([-150,150,-inf,inf]); %调制信号是fm=100,所以观察范围要将其包含进去%% *****************载波信号的时域波形*****************fc = 1000; %载波信号频率zaibo = cos(2*pi*fc*t); %载波信号时域表达式subplot(3,2,3);plot(t,zaibo,'Linewidth',1);xlabel('t/时间');ylabel('载波信号');axis([0,0.02,-1.1,1.1])%% *****************载波信号的频域波形*****************[f1,zaibof] = T2F(t,zaibo);subplot(3,2,4);plot(f1,zaibof,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度/zaibo(f)');axis([-1200,1200,-inf,inf]);%% *****************AM波信号的时域波形*****************A0 = 1; %叠加的直流分量sam = (A0+mt).*zaibo;subplot(3,2,5);plot(t,sam,'Linewidth',1);hold on;plot(t,A0+mt,'r','Linewidth',1);%画包络xlabel('t/时间');ylabel('AM调制信号幅度');title('AM调制信号及其包络');axis([0,0.02,-2.1,2.1]);%% *****************AM波信号的频域波形*****************[f2,samf] = T2F(t,sam);subplot(3,2,6);plot(f2,samf,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度/sam(f)');axis([-1200,1200,-inf,inf]);%% 相干解调%% ****************已调信号与载波信号相乘****************%信道传输中考虑噪声干扰SNR = 20; %信噪比20dBsam_noisy = awgn(sam,SNR,'measured');st = sam_noisy.*cos(2*pi*fc*t);figure();subplot(2,1,1);plot(t,st,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('已调信号与载波信号相乘');axis([0,0.02,-2.5,2.5]);%% *************已调信号与载波信号相乘的频谱*************[f,sf] = T2F(t,st);subplot(2,1,2);plot(f,sf,'r','Linewidth',1);xlabel('f/Hz');ylabel('幅度');title('AM调制信号频谱');axis([-2500,2500,-inf,inf]);%% ********************解调出来的信号********************yf = lpf(f,sf,2*fm); %经低通滤波器,滤除高频载波[t,st] = F2T(f,yf); %傅里叶逆变换figure();subplot(2,1,1);plot(t,st*2-A0,'Linewidth',1);xlabel('t/时间');ylabel('幅度');title('解调出来的信号');axis([0,0.1,-1.1,1.1]);%% ***********************原始信号***********************subplot(2,1,2);plot(t,mt,'g-','Linewidth',1); % 绘制原始基带信号title('原始基带信号'); xlabel('t/时间'); ylabel('幅度'); axis([0 0.1 -1.1 1.1]); 2.T2F.m文件,FFT功能
%傅里叶变换--FFTfunction [f,mf] = T2F(t,mt)T = t(end); %④输入信号的时间最大值df = 1/T; %③频率分辨率,由定义式df=fs/N推导可得N = length(t); %②[0, Δt, 2Δt, ..., T-Δt],t的长度就是采样点数f = -N/2*df:df:(N/2-1)*df; %①频谱图的横坐标mf = fft(mt);mf = T/N*fftshift(mf); %将0-fs频谱搬移到-fs/2-fs/2频谱,乘以T/N实现幅度归一化3.F2T.m文件,IFFT功能
%傅里叶逆变换function [t,st] = F2T(f,yf)df = f(2)-f(1); %频率间隔fmax =( f(end)-f(1)+df); %最大频率,+df是要把f(end)的值包含进去dt = 1/fmax; %时域的分辨率,可类比T2F中的频谱分辨率N = length(f); %采样点数t = 0:dt:(N-1)*dt;yf = fftshift(yf); %将0-fs频谱搬到-fs/2-fs/2st = fmax*ifft(yf); %做IFFTst = real(st); %取实部4.lpf.m文件,低通滤波功能
%低通滤波器function yf = lpf(f,sf,B)N = length(f); %采样点数df = f(2)-f(1); %频率间隔ym = zeros(1,N); %创建1×N的全零数组xm = floor(B/df); %带宽/频率间隔,向下取整,计算需要的采样点数xm_shift = [-xm:xm-1]+floor(N/2); % 因为前面做FFT将0频率搬移到中心处, % 因此,低通低频频率相应地搬移fN/2,才是对应的频率点ym(xm_shift) = 1; % 低通通过频率处幅度为1,其余为0,相当于理想低通yf = ym.*sf; %信号经过理想低通滤波器四、结果图
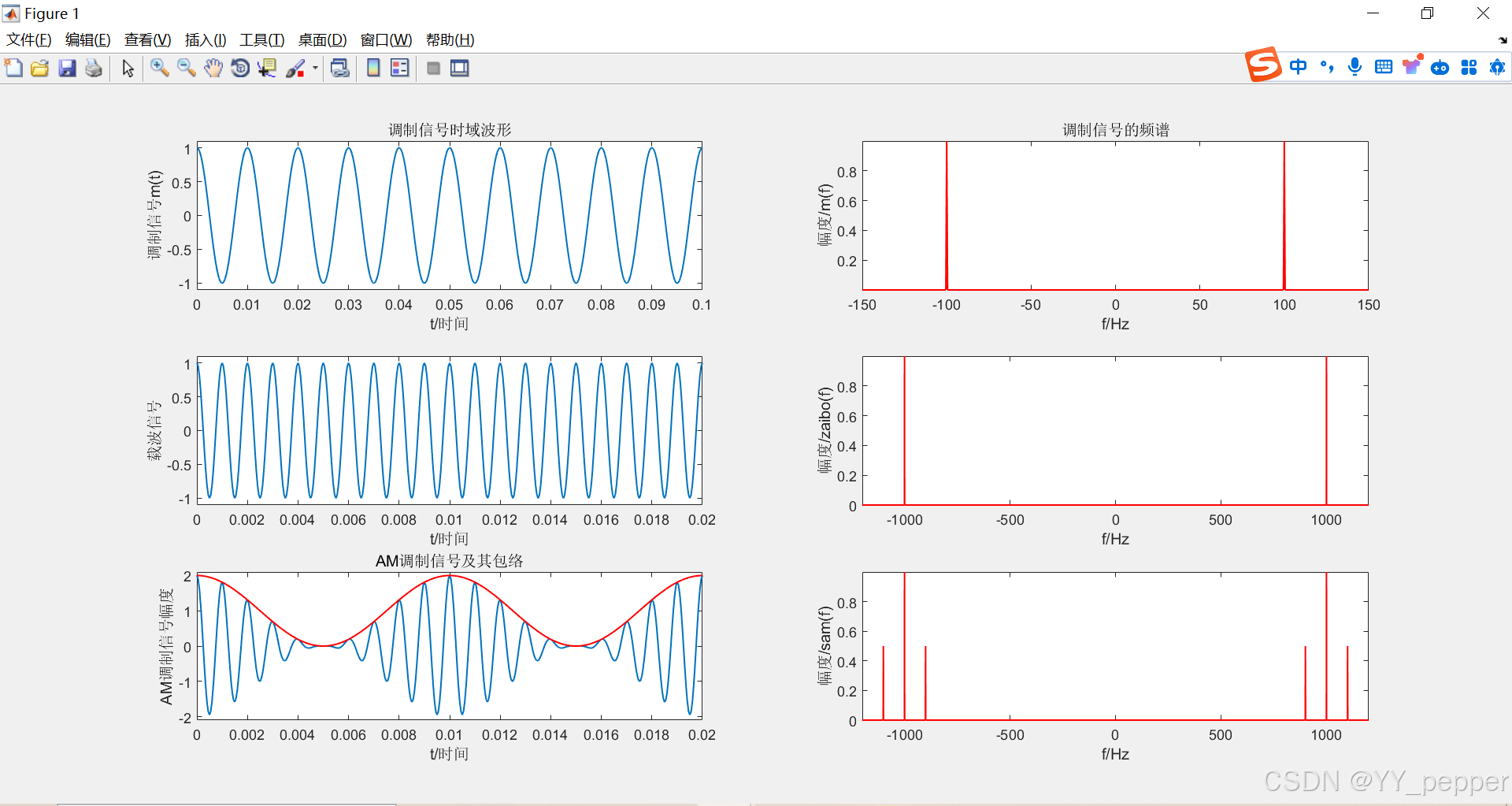
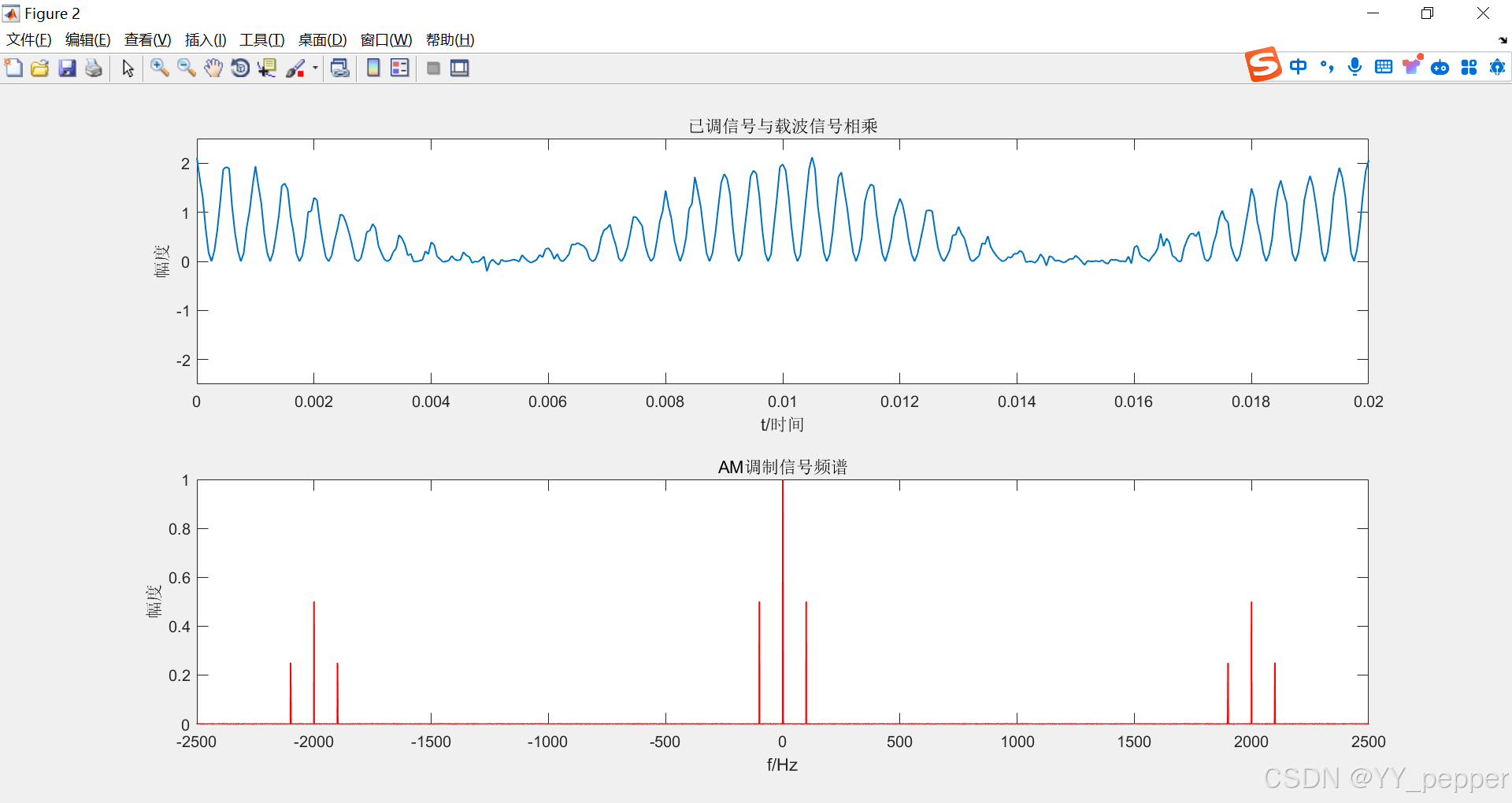
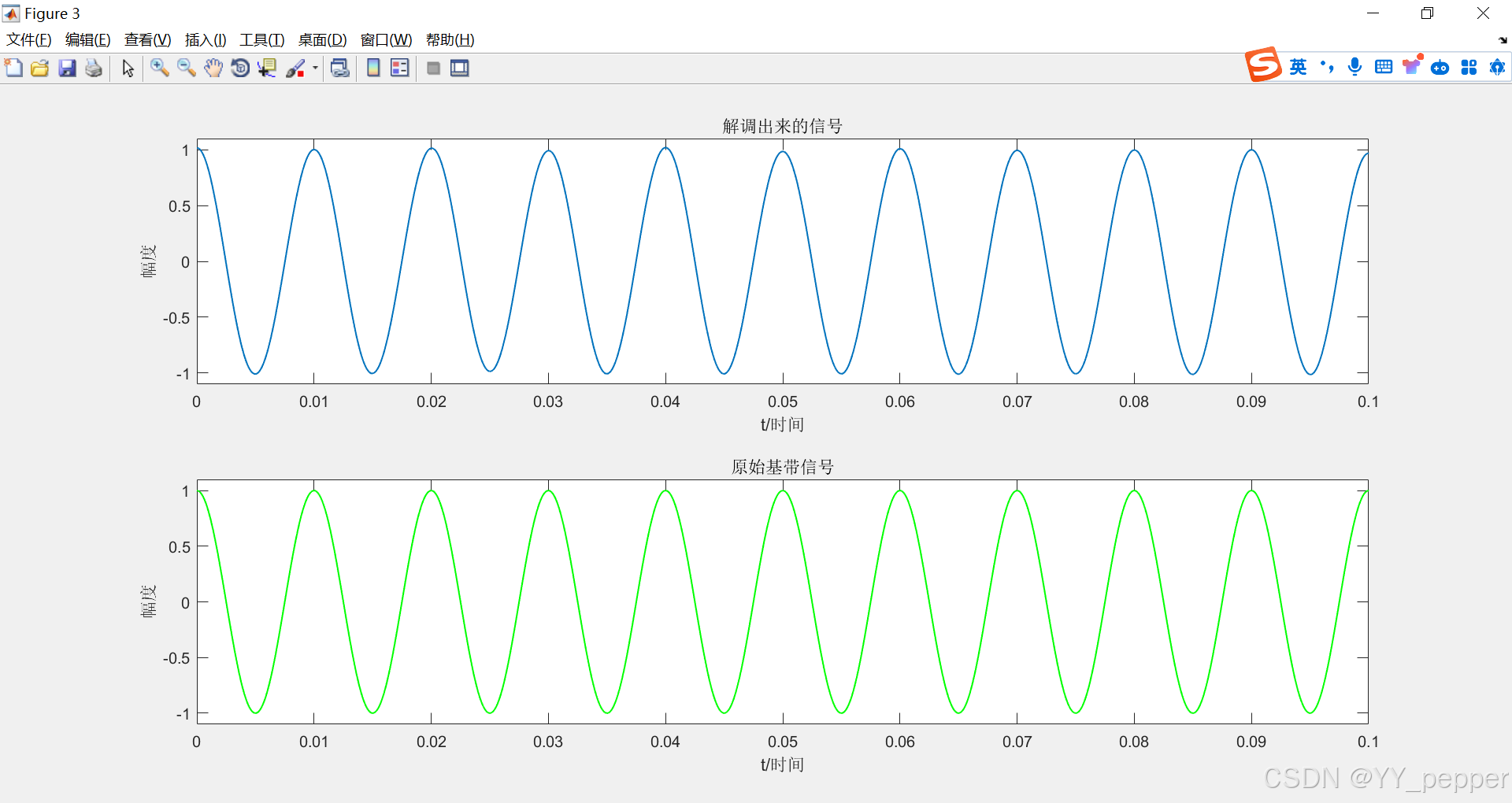
五、思考
1.采样点数 N=length(t)
在实际信号处理中,信号通常是连续的。为了在计算机中处理这种信号,我们需要将其离散化,这个过程称为采样。
假设有一个时间向量 t,表示信号的采样时间点。例如,如果 t 是从 0 秒开始,以 Δt 间隔(即采样周期)采样,直到 T 秒结束,那么 t 就是 [0, Δt, 2Δt, ..., T-Δt]。那么时间向量 t 的长度,也就是信号的采样点数。
2.频率分辨率&时域的分辨率
df = fs/N = fs/(T/dt) = fs/(T*fs) = 1/T 。类似的,dt = 1/fmax 。
3.DFT与IDFT的幅度归一化
直接计算的 FFT 输出没有经过归一化,频谱的幅度通常会比时域信号的幅度大。为了确保频谱的幅度与实际信号幅度保持一致,引入归一化。具体来说,经过适当的归一化处理后,频域中的幅度能够真实地代表时域信号的能量或振幅分布,各个频率分量的幅度准确地反映了原始时域信号在这些频率上的贡献。
| 归一化因子(简化) | 归一化因子(精确) | |
| DFT | 1/N | T/N |
| IDFT | N | fmax(频谱带宽) |
在 FFT 中的归一化,乘以T/N是为了调整由于求和过程导致的幅度膨胀。这是因为 FFT 的计算是对整个信号的加总。
![]()
在 IFFT 中的归一化,乘以 fmax 是为了补偿频谱宽度对时域信号的影响,确保信号幅度与原始信号一致。

这两种归一化的目的是相同的:确保信号在不同域之间转换时,幅度保持一致,但它们在计算方法上有所不同,因为它们适用于不同的转换过程(FFT 和 IFFT)。
4.fftshift()的理解
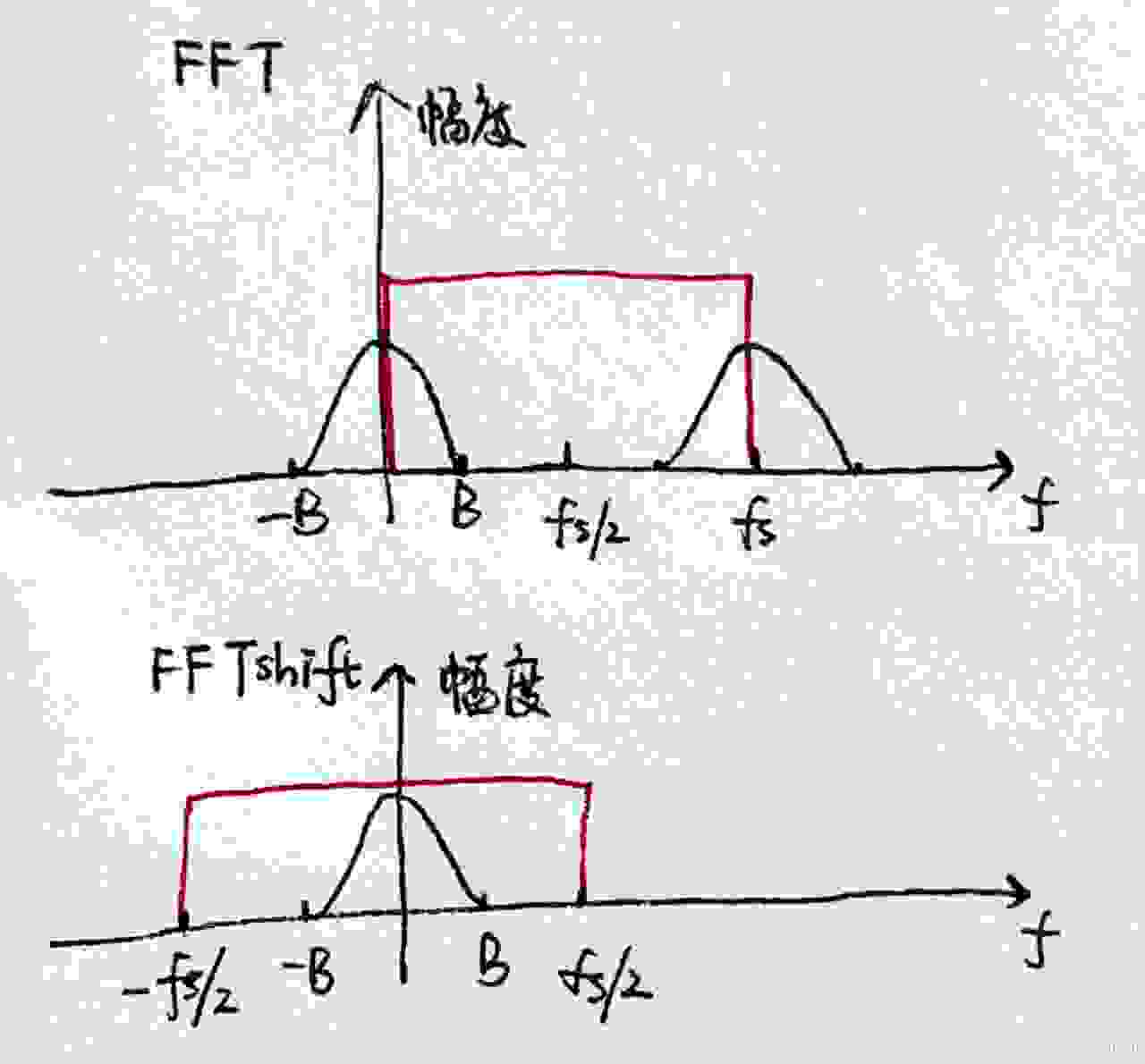
fft: 计算信号的傅里叶变换,频率分量从零到正再到负。
fftshift: 将 fft 的输出进行重新排列,调整频谱排列,将零频率分量移动到中心,使频谱更加直观对称。