三万多字长文！让你秒懂编译原理(四)——第四章 语法分析—自上而下分析

系列文章传送门：
万字长文+独家思维导图！让你秒懂编译原理(一)——第一章 引论
万字长文！让你秒懂编译原理(二)——第二章 高级语言及其语法描述
近三万字长文！让你秒懂编译原理(三)——第三章 词法分析
三万多字长文！让你秒懂编译原理(四)——第四章 语法分析—自上而下分析

编译程序总框

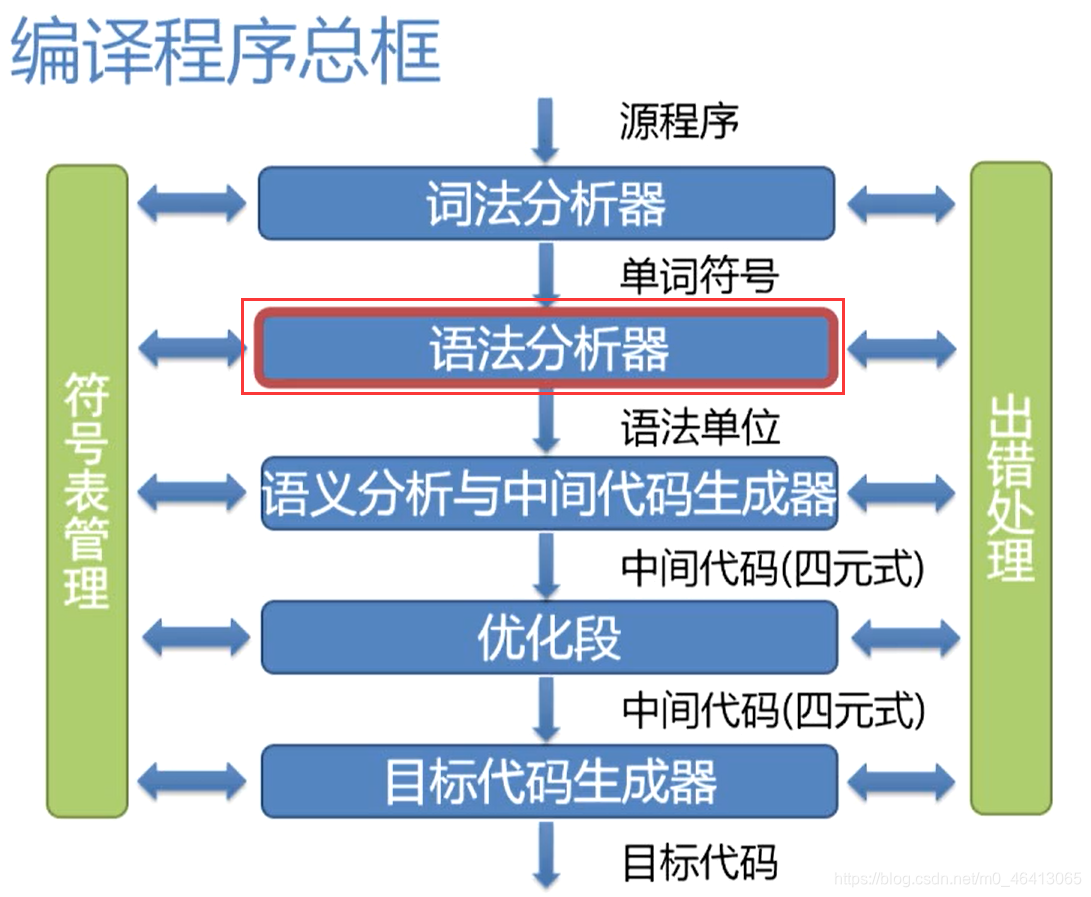
本章主要介绍语法分析的处理
要进行语法分析，必须对语言的语法结构进行描述。

回顾

• 采用正规式和有限自动机可以描述和识别语言的单词符号；
• 用上下文无关文法来描述语法规则。

注：
开始符S至少必须在某个产生式的左部出现一次。
产生式集合给出了一个非终结符的定义（→定义为）
说明这个非终结符由怎样的非终结符和终结符构成
即只要左边是非终结符，就能产生任何符
( V T ∪ V N ) (V_T∪V_N) (VT​∪VN​)表示终结符和非终结符组成的字符集合
( V T ∪ V N ) ∗ (V_T∪V_N)^* (VT​∪VN​)∗表示该集合中的符号所组成的字的全体

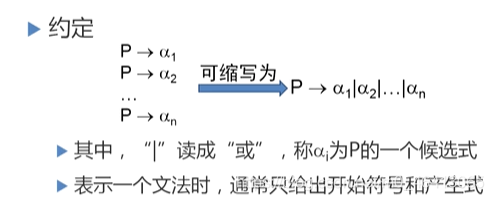
表示一个文法时，通常只给出开始符号和产生式，如上例，可表示为：
G(E)： E → i | E+E | E*E | (E)

把一个字符串中的一个终结符的一次出现（不是所有一起替换）替换成候选

句子也是句型

要证明是一个句子，必须证明它只有终结符，即只有{i，+，*，(，)}，然后再证明他能从文法开始的符号推出来。

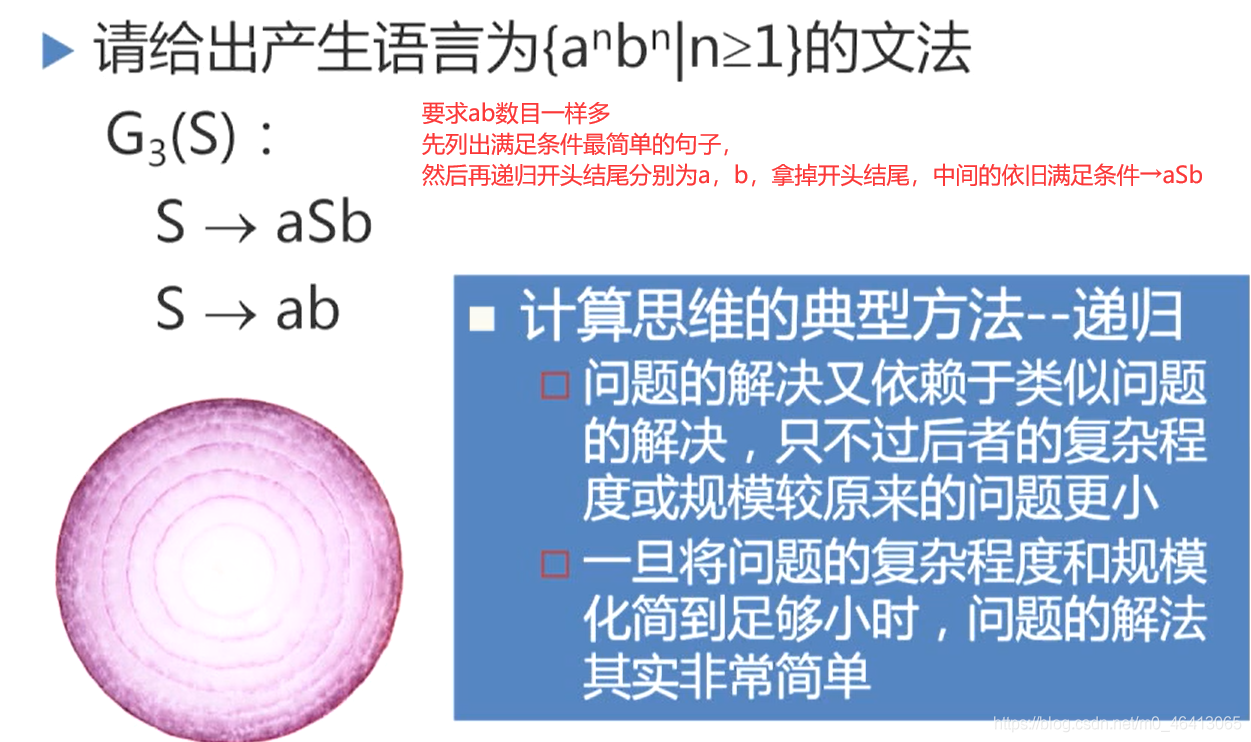
4.1 语法分析器的功能

• 语法分析的任务是分析一个文法的句子结构。
• 语法分析器的功能：按照文法的产生式(语言的语法规则)，识别输入符号串是否为一个句子(合式程序)。
  注：语法分析是编译程序的核心部分

语法分析器在编译器中的地位

编译程序有词法分析器、语法分析器、符号表等模块。
编译程序中起主导或驱动作用的是语法分析器

1. 语法分析器需要下一个单词的时候需要调用词法分析器，即词法分析子程序
2. 词法分析器从源程序当前位置开始处理
3. 按照词法规则，识别出一个单词符号，将单词符号返回给语法分析程序
4. 语法分析器拿到这个单词后，继续开展语法分析，得到一部分语法树，交给编译程序后续部分进行分析处理
5. 如果分析处理不下去了，需要读入下一个单词的时候， 语法分析器就会继续调用词法分析器，取得下一个单词，语法分析器就继续工作下去

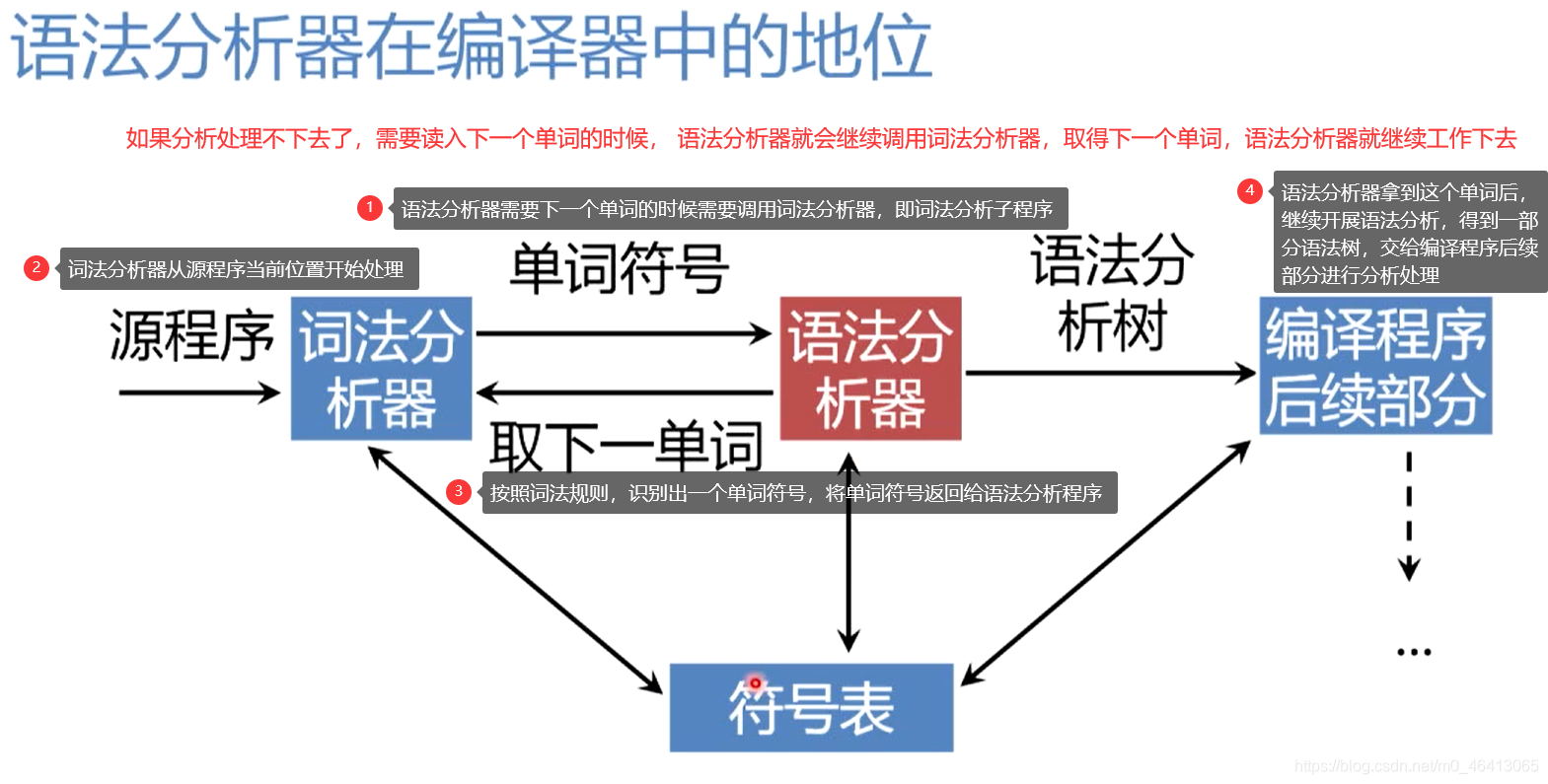
在整个分析过程中，语法分析器，词法分析器都会跟符号表打交道，在符号表中记录，访问，修改编译过程的信息，所以语法分析器在编译程序中处于主导地位

语法分析的方法：

自下而上分析法(Bottom-up)

• 基本思想：从输入串开始，逐步进行“归约”，直到文法的开始符号。即从树末端开始，构造语法树。
• 所谓归约，是指根据文法的产生式规则，把产生式的右部替换成左部符号。
• 算符优先分析法：按照算符的优先关系和结合性质进行语法分析。适合分析表达式。
• LR分析法：规范归约
  

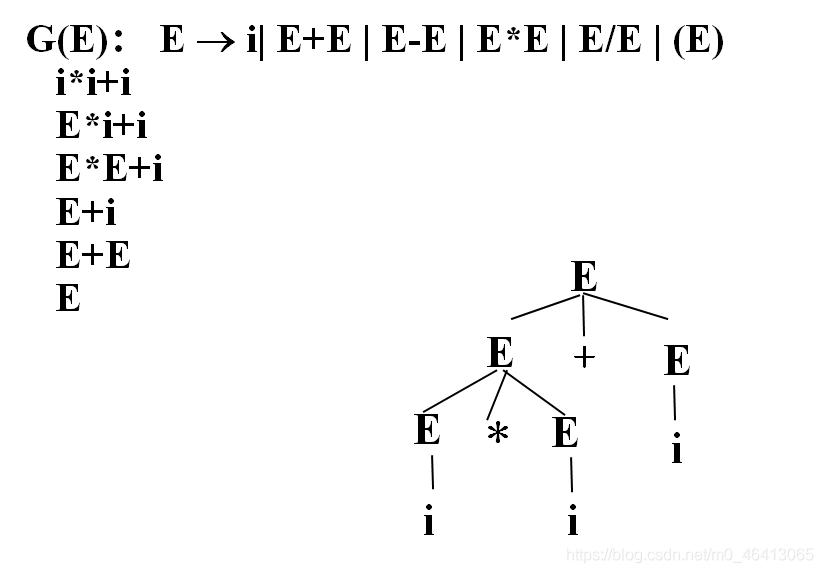
自上而下分析法(Top-down)

• 基本思想：它从文法的开始符号出发，反复使用各种产生式，寻找"匹配"的推导。

• 递归下降分析法：对每一语法变量(非终结符)构造一个相应的子程序，每个子程序识别一定的语法单位，通过子程序间的信息反馈和联合作用实现对输入串的识别。

• 预测分析程序
  优点：直观、简单和宜于手工实现

• 自上而下就是从文法的开始符号出发，向下推导，推出句子。
  ①带“回溯”的
  ②不带回溯的递归子程序(递归下降)分析方法。

• 自上而下分析的主旨：对任何输入串，试图用一切可能的办法，从文法开始符号(根结点)出发，自上而下地为输入串建立一棵语法树。或者说，为输入串寻找一个最左推导。

4.2 自上而下分析(Bottom-up)及其面临的问题

基本思想

• 从文法的开始符号出发，向下推导，推出句子
• 针对输入串，试图用一切可能的办法，从文法开始符号(根结点)出发，自上而下地为输入串建立一棵语法树

匹配过程

先由树的根结点，从S出发，向下推导，从左到右跟x*y匹配。
有一个IP指针，相当于词法分析器，每调用一次词法分析器，就返回一个单词，指针就往前进一个。
从x开始推导，S本身无法跟x匹配，将S扩展为它的定义式x,A,y
x与x匹配（都是同一个终结符），匹配成功。

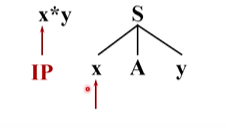
语法分析器前进，读入下一个单词 * ，语法树由小x后面的符号开始，去跟输入串后面的 * 匹配，因此匹配指针也向后移动，由x到A，A与*匹配，非终结符与一个终结符没法直接匹配

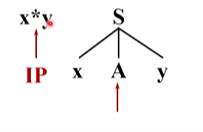
只能把这个非终结符替换成它的定义式，A有两个定义式，选择第一个候选**来扩展A，左边的 *能够与输入串当前的单词 * 匹配（两个为同一个终结符）

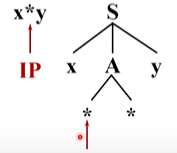
然后两个指针均向后移动，注意到语法树中第二个 * 和输入串当前的单词都是终结符，且不同。 *没办法替换成别的符号，所以分析无法进行

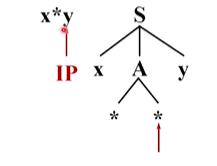
回溯，将A替换为第二个候选，两个 * 匹配成功，前进

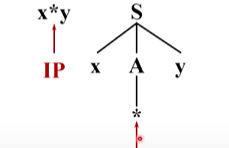
这时候输入串指向y，语法树也是指向y，匹配成功

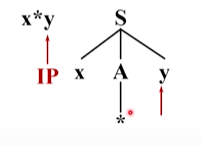
多个产生式候选带来的问题

某个非终结符有多个产生式候选时，可能带来如下问题:

1. 回溯问题

• 分析过程中，当一个非终结符用某一个候选匹配成功时，这种匹配可能是暂时的。
• 出错时，不得不 “回溯”。

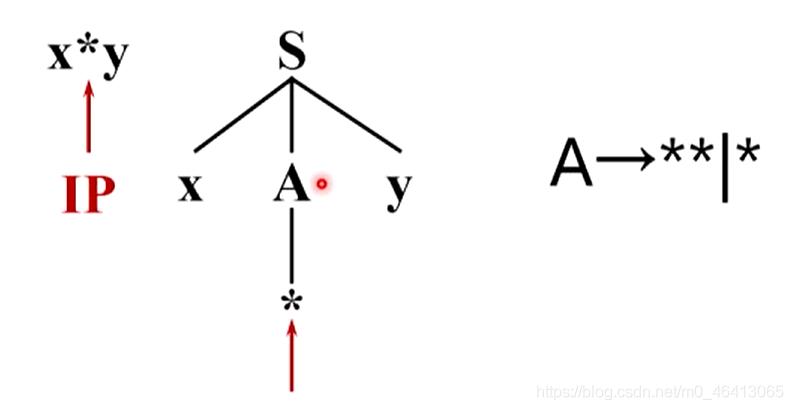
待回溯的分析程序设计起来非常麻烦，我们希望得到不需要回溯的分析程序，也就是确保我们每一次在多个候选做选择的时候，都是唯一可能正确的

2. 文法左递归问题。

• 一个文法是含有左递归的，如果存在非终结符P
  
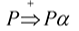
  P经过一步/多步推导之后，能推出一个串，这个串以其自身开头，后面可以是任意串。(左递归)

从文法开始符号出发向下推导:
推导到P，并在左递归的这条通路上依次扩展下去，向下扩展的过程中，单词符号没有读入任何新的符号，没有任何推进，但这个树不断向下增长
导致语法树不断生长，而单词的语法树不断前进，最后导致整个分析器陷入死循环。

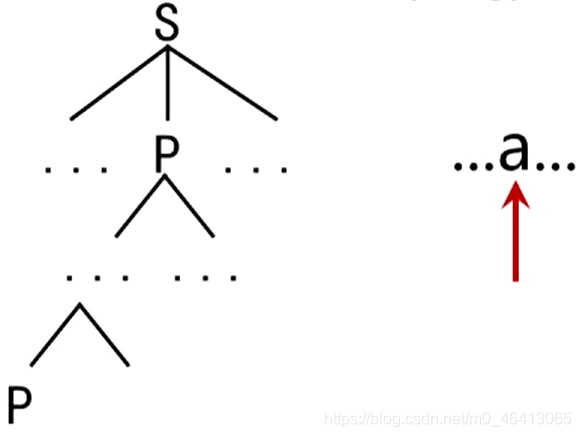
含有左递归的文法将使自上而下的分析陷入无限循环。

4.3 LL(1)分析法

构造不带回溯的自上而下分析算法

• 要消除文法的左递归性
• 克服回溯

4.3.1 左递归的消除

两个候选

多个候选

E和T都有直接左递归。

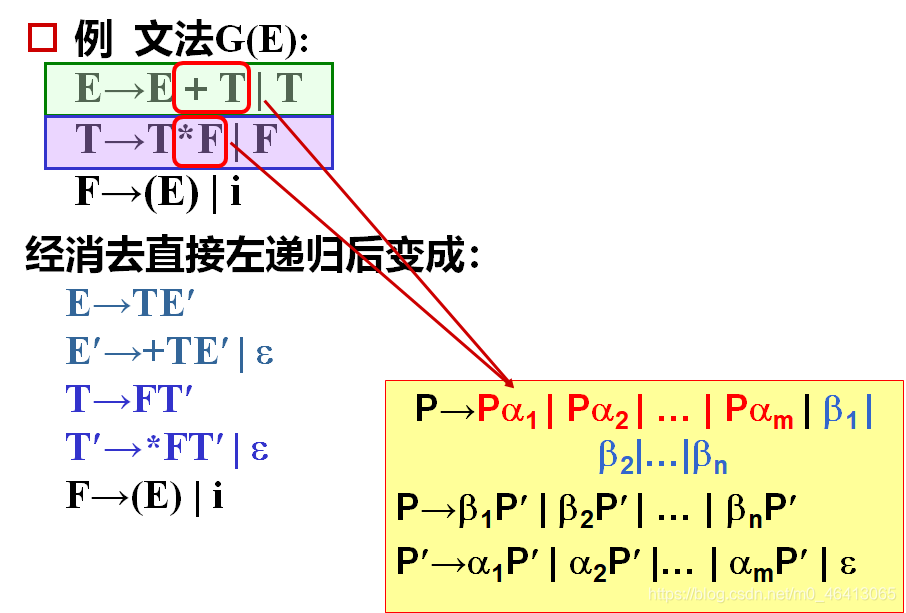
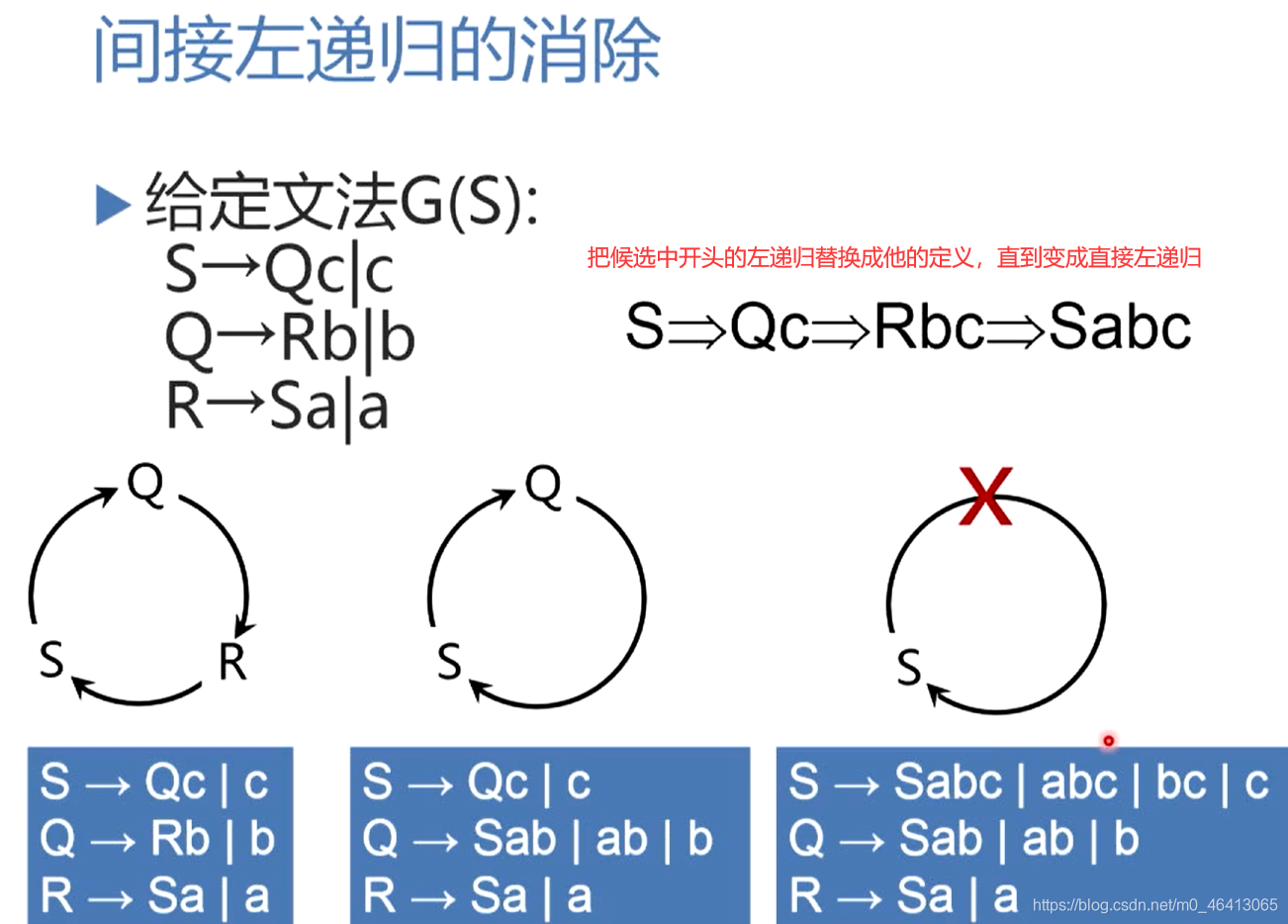
把候选中开头的左递归替换成他的定义，逐步减少定义种圈中的节点，最后变成自圈，从而变成直接左递归。

构造一个循环，使之达到这样的一个目的：
使Pi的规则要么以终结符开头，如果以非终结符开头，只能以排在Pi后面的这些非终结符开头。也就是说Pi的定义不能出现有在这个序列当中排在他前面的非终结符开头的这种定义式（候选式）

在循环体内嵌一个循环j(1 ~ i-1)，处理Pi的产生式，如果Pi定义候选以Pj开头，将Pj替换成他的定义式，（当处理Pi的时候，P1 ~ Pi-1已经达到上述目标规则形式，也就是Pj的定义式符合上述：要么以终结符开头，如果以非终结符开头，只能以排在Pj后面的这些非终结符开头）,从而使Pi要么以终结符开头，要么以Pj后面的非终结符开头，当j一直循环，Pi也达到目标规则形式：要么以终结符开头，如果以非终结符开头，只能以排在Pj后面的这些非终结符开头

这个时候Pi如果有Pi开头的候选极为直接左递归。按照直接左递归做法消除左递归。

即：

4.3.2 消除回溯、提左因子

• 产生回溯的原因：
  推导时，若产生式存在多个候选式，选择哪个进行推导存在不确定性。
• 为了消除回溯就必须保证：
  对文法的任何非终结符，当要它去匹配输入串时，能够根据它所面临的输入符号准确地指派它的一个候选去执行任务，并且此候选的工作结果应是确信无疑的。

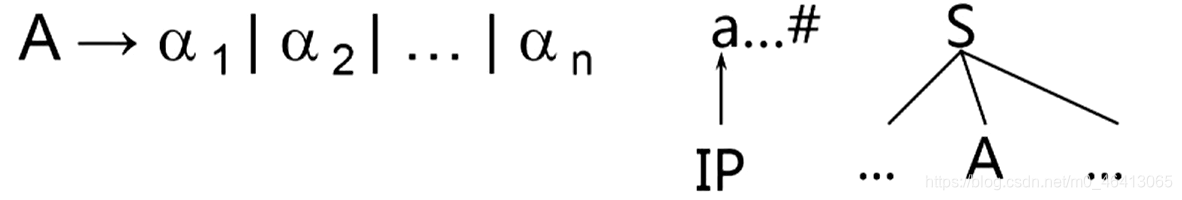
任务：根据当前的输入符号a在当前A的所有候选中准确的指出一个候选去扩展A

如何选择？

如果当前A的所有候选，有且只有一个是以a(当前单词)开头的话就毫不犹豫选择这个候选。

即根据当前的单词符号去看他出现在哪一个候选的开头，如果有一个候选的开头是终结符且恰好是该单词符号的话就选它(a)

如果候选的开头都是非终结符，非终结符能推出当前单词开头的(a)的串

FIRST集合

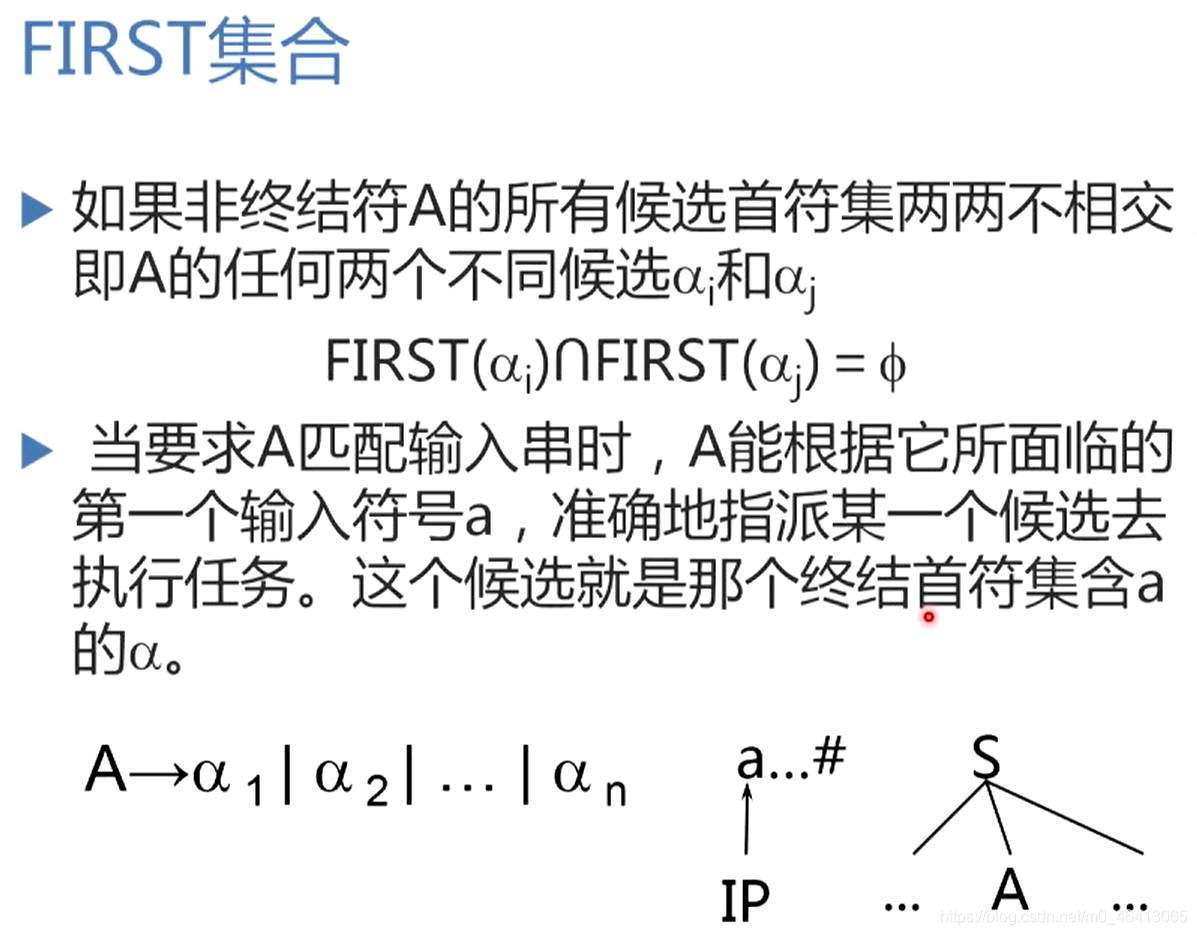
提取公共左因子:

一个文法可能开始并不具备，非终结符的首符集两两不相交的情况一开始可能不成立，因此我们需要用一个算法进行改造——提取公共左因子，使得候选尽可能的不相交。

4.3.3 LL(1)分析条件

ε候选

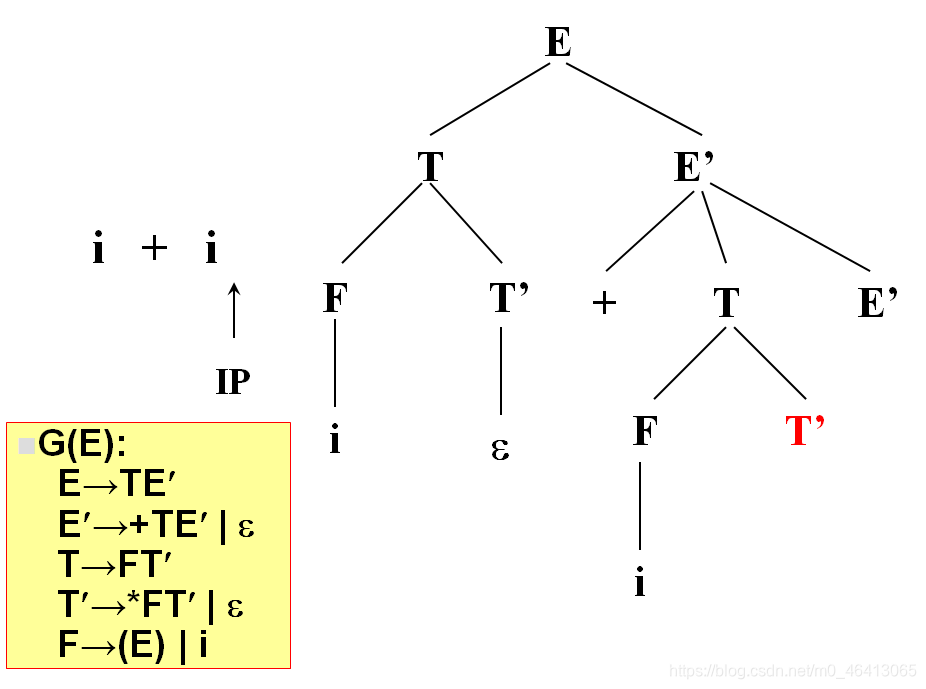
开始时，当前符号为i，自上而下分析，从文法的开始符号开始E作为树的根，向下扩展

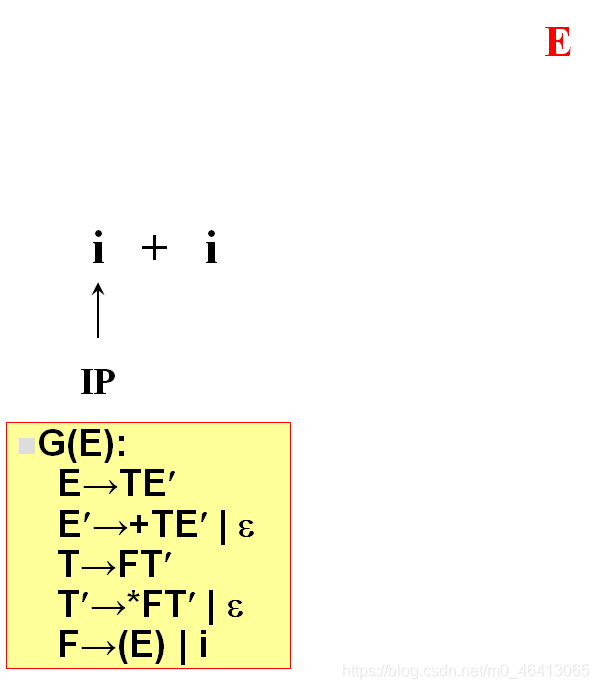
T,E’（唯一候选）

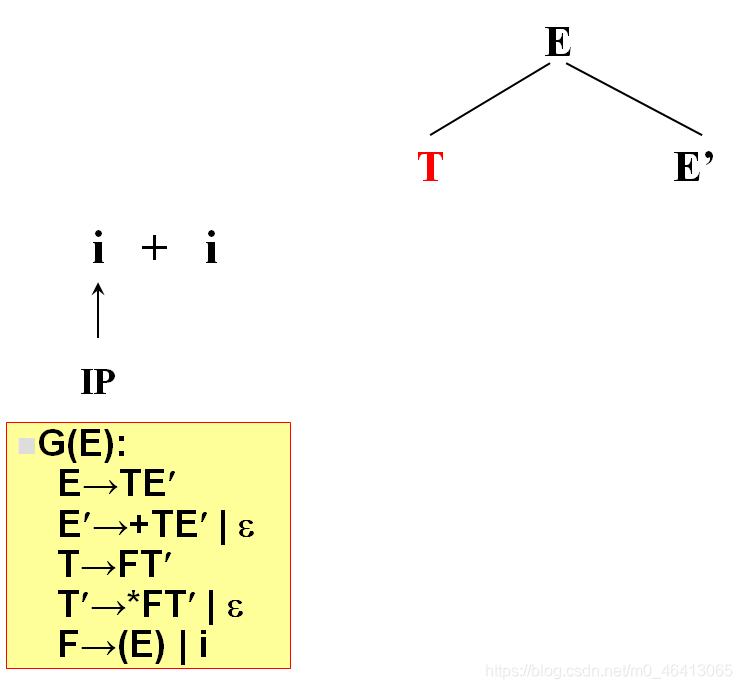
T为非终结符，对T进行扩展，T只有唯一的候选F，T’

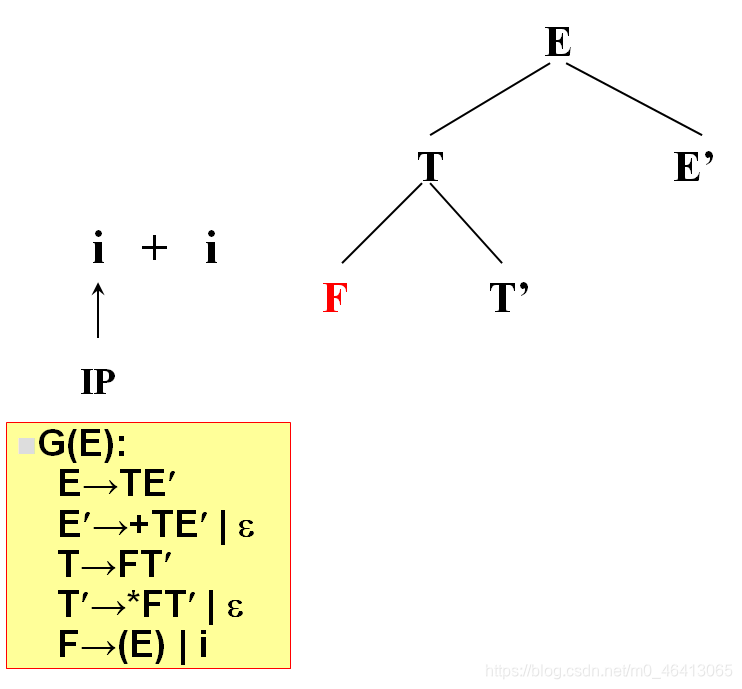
由F匹配i，F为非终结符，向下扩展，有两个候选（E）和i，根据当前字符i，选候选，选择依据为每个候选的FIRST集合，二者分别为(和i，i匹配，选i，与输入单词为同一个符号，匹配成功，读入下一个符号

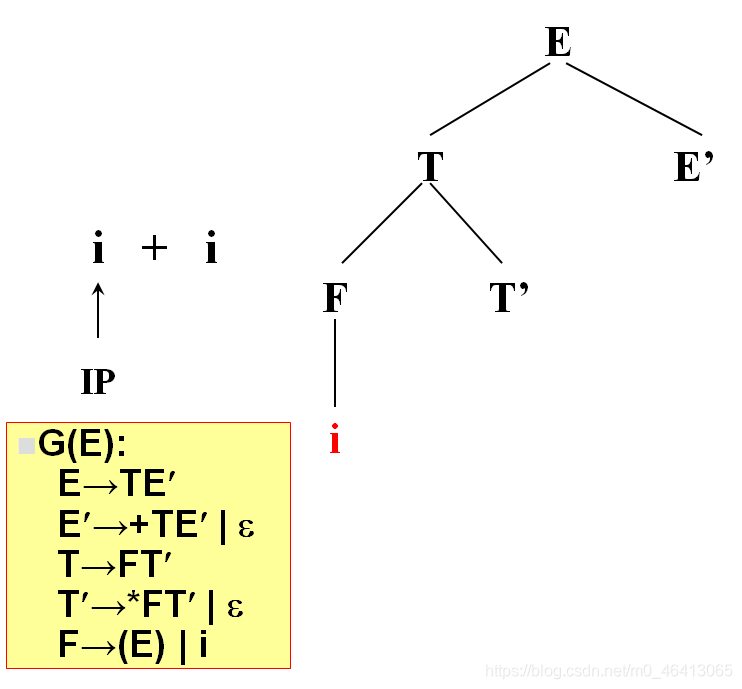
+由T’来匹配，T’有两个候选，* FT’和ε，由于+无法与 * FT’匹配，因此只能选择ε

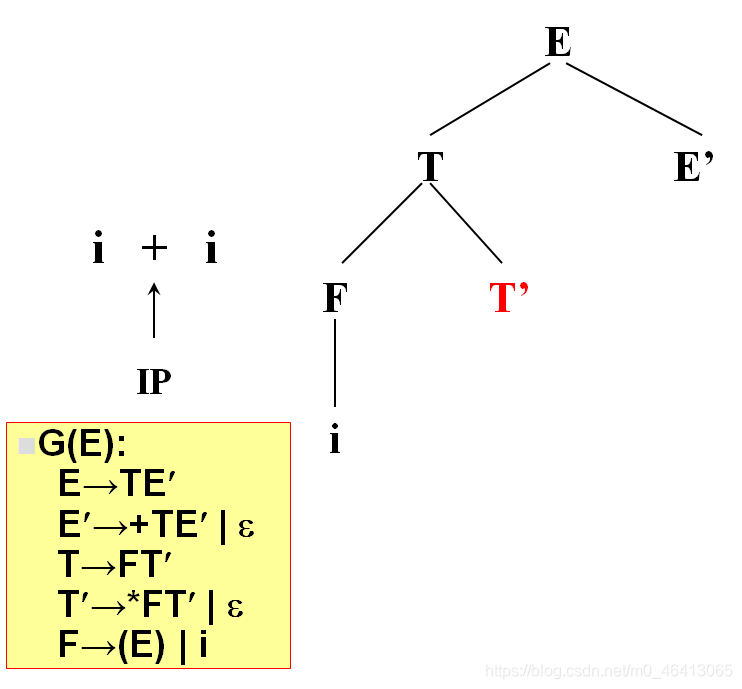
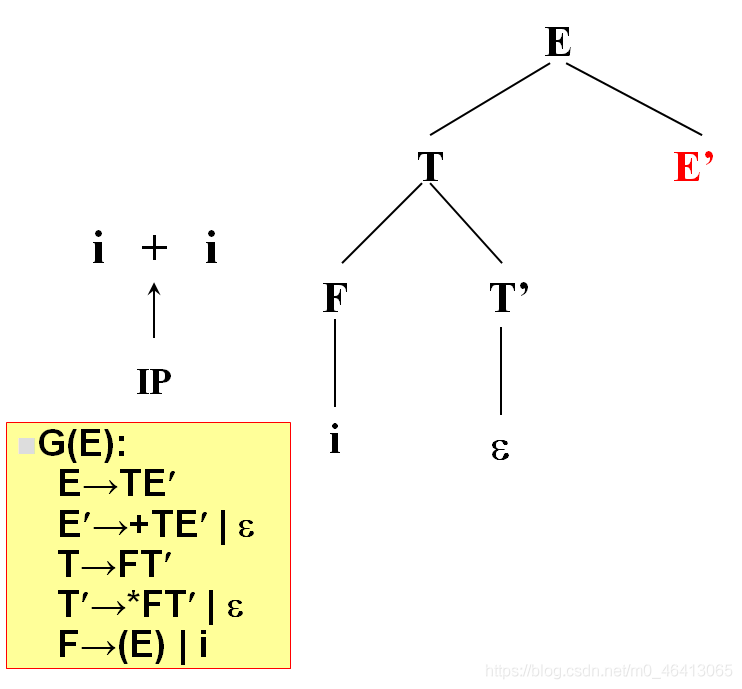
+由E’来匹配，E’有两个候选，+TE’和ε，+与第一个候选的首符集相同，E’扩展成+TE’。
+匹配成功，读入下一个字符。

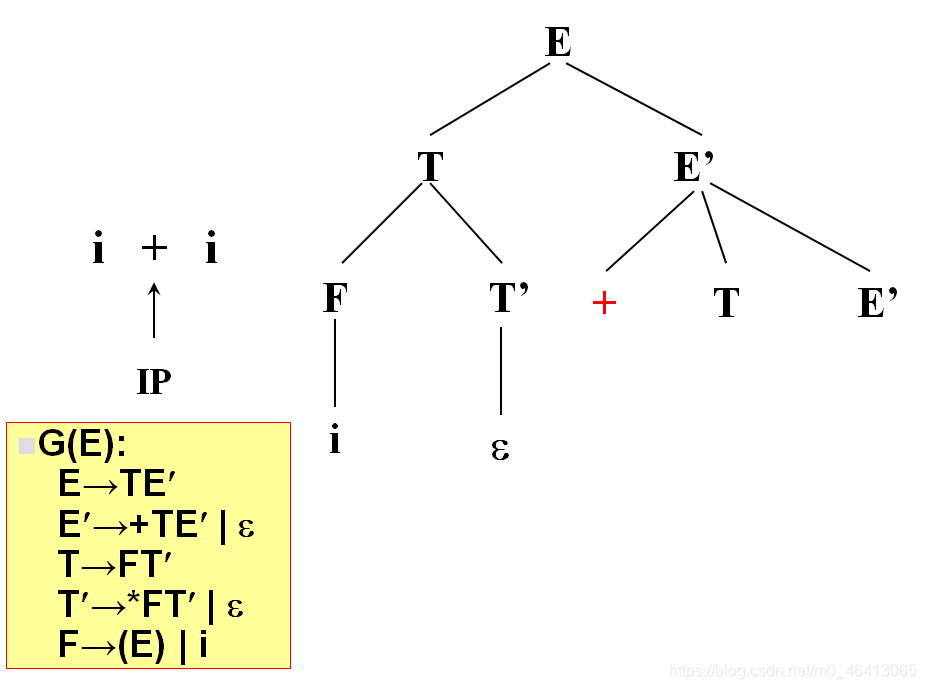
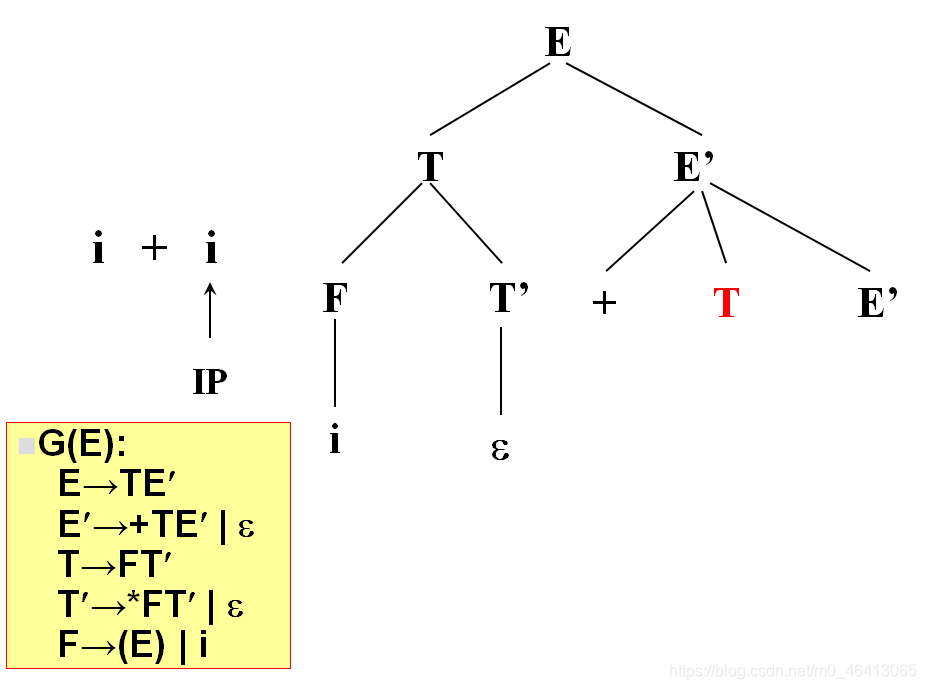
i与T匹配，T扩展FT’,F扩展为i与i匹配成功，

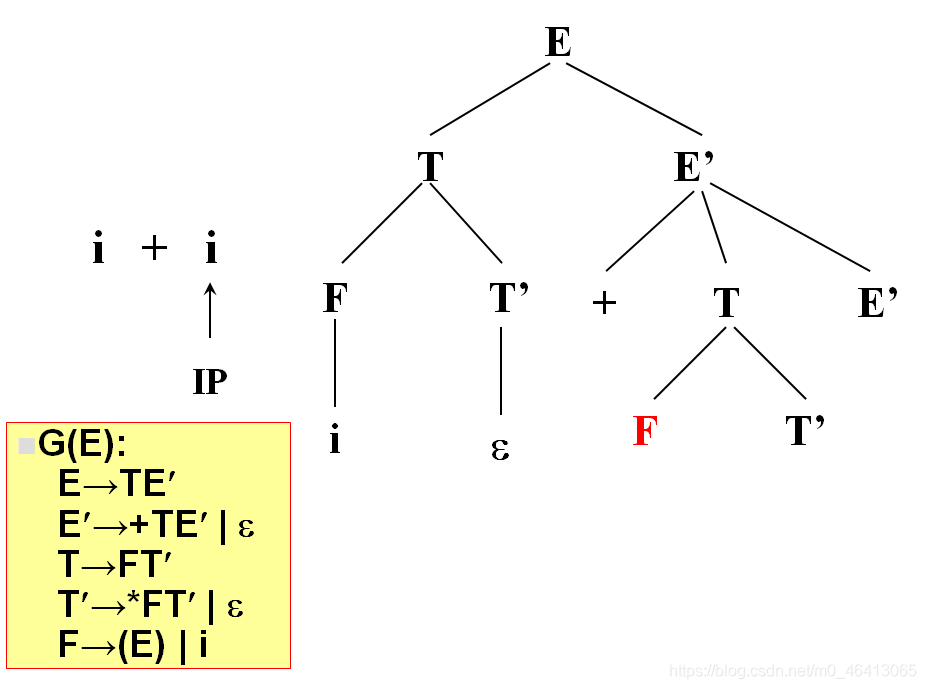
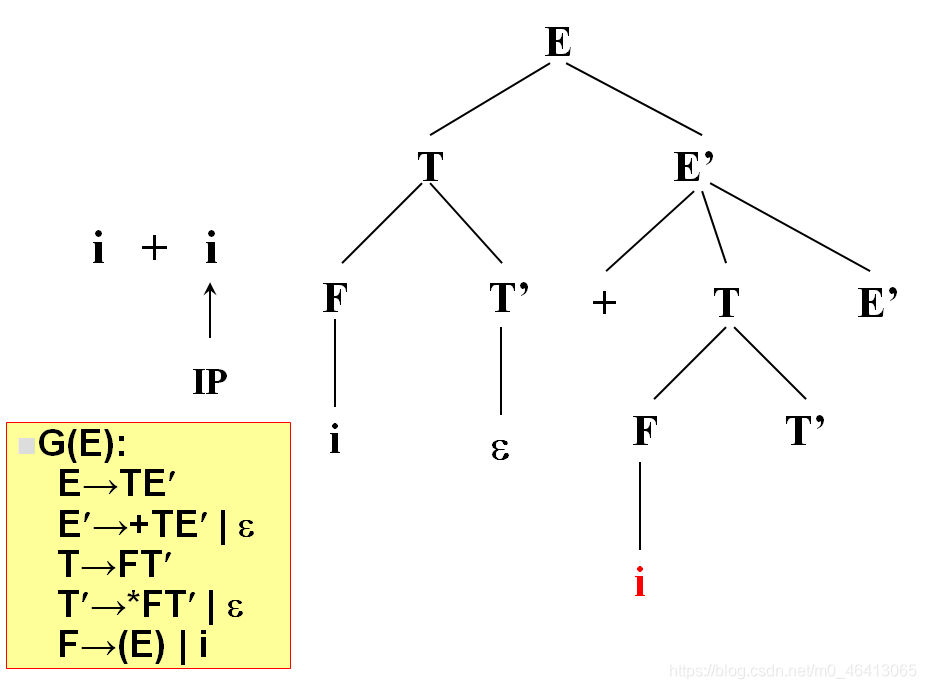
没有字符了，因此后面都用ε匹配



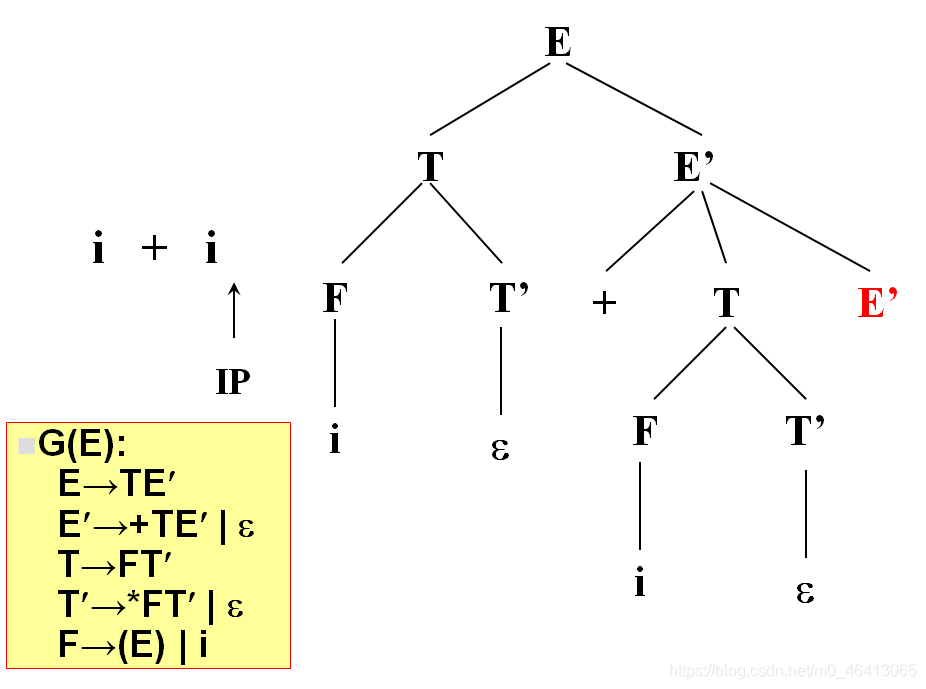
匹配完了，得到分析树

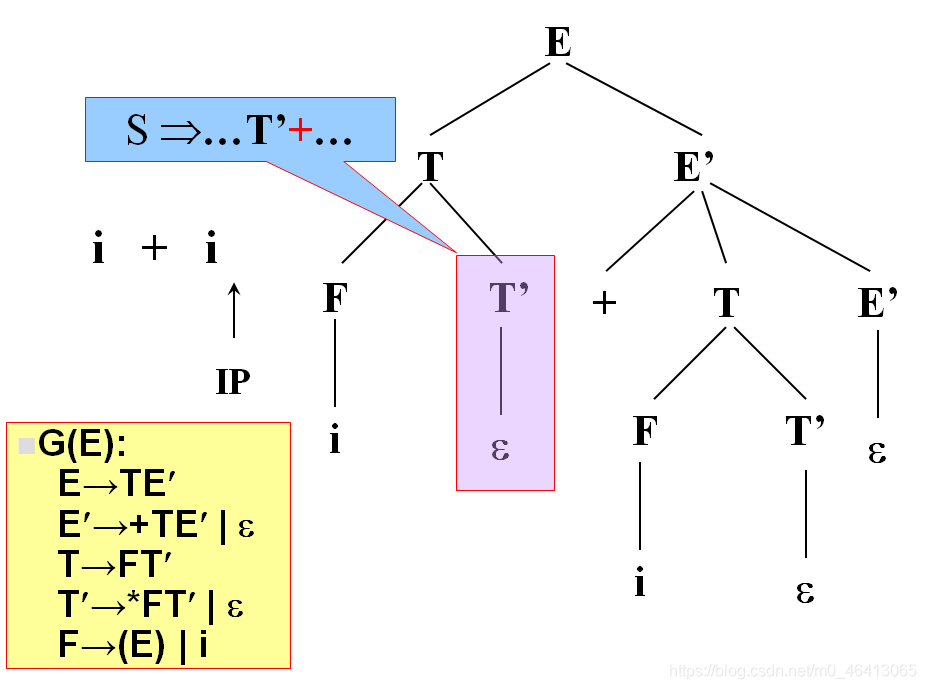
当T’替换成ε时，我希望T’不匹配任何一个单词，即我希望+由T’后面的去匹配，也就是当时能匹配的成功的条件是：
这个文法存在一种句型，在这个句型里面，+能跟在T’后面，所以T’替换成ε，后面有人去匹配+

下面要把当前的终结符是不是在某一个句型里能跟在非终结符后面这个事情说清楚

定义集合——FOLLOW集合

FOLLOW集合

总结一下，如果一个非终结符A，A有多个候选，当面临输入符号a要用A去匹配的时候，且a不在A的任何一个首符集里面，但有一个候选是ε，或首符集有ε（候选推着推着就能变成ε，可以看成ε），但这个并不一定能把A替换成ε。
还有条件，要求a一定在某个句型的时候能够跟在A的后面，才能选择A的ε候选去扩展A

如果把和每个非终结符都有这种相关性的终结符构成一个集合——FOLLOW集合

能够在某个句型里面，跟在A后面的终结符都在A的FOLLOW集合里面。
瞄着ε匹配的条件来的

注意：如果S能够推出A结尾的一个串的句型，则#(句子末尾)也属于A的FOLLOW集合。

LL(1)文法

一个文法先消除左递归，再消除左公共因子，然后再验证它是不是满足这三个条件，满足LL(1)文法的条件就可以用LL(1)分析法：

LL(1)分析法

每一个分析动作都是确定无疑的，这样就不需要回溯，同时我们文法也没有左递归，也不用担心陷入无限循环。

FIRST集合和FOLLOW集合的构造

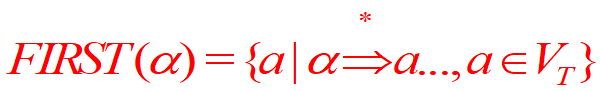
α的FIRST集合，是指这个串能够推出的任意串中间，排在开头位置的终结符构成的集合

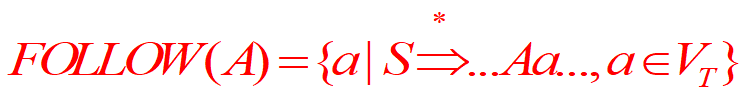
一个非终结符的FOLLOW集合是指在某个句型里面，能够跟在非终结符后面的终结符构成的集合

FIRST集合的构造

对α的情况进行分类讨论

• α长度是1，要么是终结符要么是非终结符
• α长度大于1，由n个符号构成，这n个符号长度要么是终结符，要么是非终结符

FIRST集合定义是基于推导的，如果要计算一个α的所有的FIRST集合里面的元素，理论上要遍历非常大的推导空间，甚至是无穷大的推导空间，才能保证不会遗漏可能的终结符。

把对无穷推导可能的考察转换为对有限产生式的反复扫描(因为推导过程都是对有限产生式的反复使用)，对有限产生式的反复扫描从而找到FIRST集合里面的元素。

构造每个文法符号的FIRST集合

注，从第一个产生式开始，判断三个条件，更新FIRST集合，再处理下一个产生式，再处理下一个产生式，到最后一个产生式，如果从第一个产生式到最后一个产生式的考察过程中，有任意一个符号的FIRST集合发生变化，都要重新从第一个产生式再次考察。直到考察到最后一个产生式。
直到从第一个产生式扫描到最后一个产生式，没有任何一个FIRST集合发生变化了（哪怕只有一个符号的FIRST集合发生变化，都要重头开始扫描）

构造任何符号串的FIRST集合

先把X1FIRST集合中的ε拿掉

FOLLOW集合的构造

一个非终结符的FOLLOW集合是指在任何一个句型当中能够跟在非终结符后面的终结符构成的集合

FOLLOW集合的定义也是跟推导相关，也涉及到非常大都推导空间，或者是无穷大的推导空间的考察，他的构造的基本思想也是和FIRST集合一样,把对无穷推导可能的考察转换为对有限产生式的反复扫描(因为推导过程都是对有限产生式的反复使用)，来计算每一个非终结符的FOLLOW集合。

注，从第一个产生式开始，进行扫描，看看满足这三步中的哪一步，满足哪一步就修改相应的FOLLOW集合，再处理下一个产生式，再处理下一个产生式，到最后一个产生式，如果从第一个产生式到最后一个产生式的考察过程中，只要有任意一个非终结符的FOLLOW集合发生变化，都要重新从第一个产生式开始到最后一个产生式再次扫描。直到从第一个产生式扫描到最后一个产生式，在整个这一遍的过程中没有任何一个FOLLOW集合发生变化了（哪怕只有一个符号的FOLLOW集合发生变化，都有可能导致其他的发生变化，都要重头开始扫描）

举例

构造FIRST集合（详细步骤）

回顾构造方案：

挨个分析，初始时 ，每个非终结符的FIRST集合为空

根据FIRST集合计算算法
处理第一个产生式：E→TE’
符合算法第3大步
第一小步：

则把FIRST(T)中的所有非ε-元素都加到FIRST(E)中；

但FIRST(T)目前没有元素，没法加
第二小步：
但FIRST(T)目前不确定有没有ε，所以也没有变化

处理第二个产生式：E’→+TE’| ε

根据第一个候选+TE’

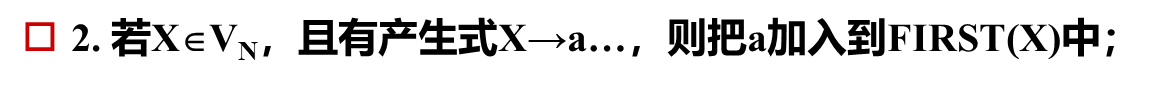
将加号加入FIRST(E’)

根据第二个候选：ε

处理第三个产生式：T→FT’

符合算法第3大步
第一小步：

则把FIRST(F)中的所有非ε-元素都加到FIRST(T’)中；

但FIRST(F)目前没有元素，没法加

处理第四个产生式：T’→FT’| ε

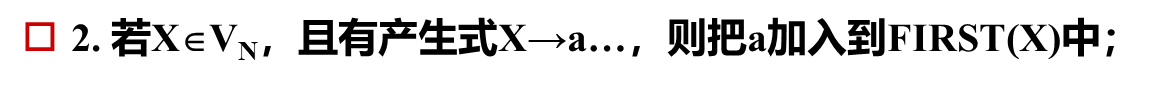
将加入FIRST(T’)

根据第二个候选：ε


处理第五个产生式（最后一个）：F→(E)| i

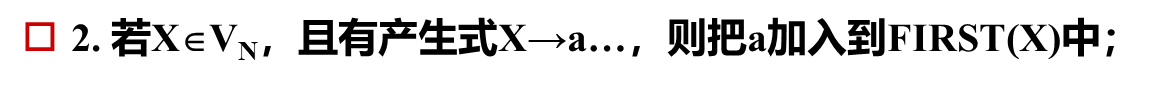
将 ( 和 i 加入FIRST(F)中

再从头到尾再把产生式扫描一遍
也就是第二遍的过程
在这一遍中
处理第三个产生式：T’→FT’

符合算法第3大步
第一小步：

则把FIRST(F)中的所有非ε-元素都加到FIRST(T’)中；

其余没变化。
也就是第二遍扫描，FIRST集合发生了变化，还得重新再扫描一遍

在第三遍扫描中
处理第一个产生式：E→TE’
符合算法第3大步
第一小步：

则把FIRST(T)中的所有非ε-元素都加到FIRST(E)中；
第三遍的时候FIRST(E)发生了变化，因此再扫描一遍
第四遍扫描，所有FIRST集后都没有发生变化，可以停止

构造FOLLOW集合（详细步骤）

回顾构造方案：

对于非终结符 E
这是文法的开始符号，按照算法的第一个步骤，#应该在E的FOLLOW集合中，然后看每个产生式的定义

E→TE’
符合算法第二步骤模式：

α为空，B为T，E’为β
FIRST(E’)={+, ε}
FIRST(E’)/{ε}={+}
得到

注意，在求FOLLOW集合的过程中一个产生式可以套上算法的2/3步多种模式，因此需要格外小心反复检查

E→TE’
也符合算法第3步骤模式：

意味着FOLLOW(E)集合中的元素要加到FOLLOW(E’)中

同时又符合第三步骤或的情况
E为A，α为空，B为T，E’为β
且正好ε∈FRIST(E’)，所以到时候推到的时候E’可能会推没了，因此FOLLOW E的也能FOLLOW T,所以算法 FOLLOW(E)集合中的元素要加到FOLLOW(T)

对于E’定义：E’→+TE’| ε
符合算法第二步骤模式：

α为+，B为T，E’为β
FIRST(E’)={+, ε}
FIRST(E’)/{ε}={+}
这个跟刚刚第一步的过程一样，没有变化
E→TE’
也符合算法第3步骤模式：

A→αB模式,α为+T，B为E’
意味着FOLLOW(E‘)集合中的元素要加到FOLLOW(E’)中

A→αBβ模式，α为+，B为T，E’为β
FIRST(E’)中有ε，把FOLLOW(E‘)集合中的元素要加到FOLLOW(T)中

但上述两步没变化

E’还有一个候选式ε，它队FOLLOW集合的运算没有直接影响。

处理第三个产生式：T→FT’
这个告诉我们FOLLOW T的都可以FOLLOW T’
由算法的第三步：

把FOLLOW(T)加入导FOLLOW(T’)中

由于ε∈FIRST(T’)，由步骤3的第二种情况，
FOLLOW T的还能FOLLOW F

同时T→FT’还符合步骤2

即FIRST(T’)中的非空符号都能FOLLOW F

再检查第4个产生式：T’→*FT’|ε
由算法的2，3步发现没有变化。

再检查第5个产生式：F→(E)| i
根据算法第二大步


根据算法的第三大步
再进行第二遍检查:

E→TE’
也符合算法第3步骤模式：

意味着FOLLOW(E)集合中的元素要加到FOLLOW(E’)中

同时又符合第三步骤或的情况
E为A，α为空，B为T，E’为β
且正好ε∈FRIST(E’)，所以到时候推到的时候E’可能会推没了，因此FOLLOW E的也能FOLLOW T,所以算法 FOLLOW(E)集合中的元素要加到FOLLOW(T)

对于E’定义：E’→+TE’| ε（第1，2遍都没有任何变化）
符合算法第二步骤模式：

α为+，B为T，E’为β
FIRST(E’)={+, ε}
FIRST(E’)/{ε}={+}
这个跟刚刚第一步的过程一样，没有变化
E→TE’

也符合算法第3步骤模式：

A→αB模式,α为+T，B为E’
意味着FOLLOW(E‘)集合中的元素要加到FOLLOW(E’)中

A→αBβ模式，α为+，B为T，E’为β
FIRST(E’)中有ε，把FOLLOW(E‘)集合中的元素要加到FOLLOW(T)中

但上述两步没变化

E’还有一个候选式ε，它队FOLLOW集合的运算没有直接影响。

处理第三个产生式：T→FT’
这个告诉我们FOLLOW T的都可以FOLLOW T’
由算法的第三步：

把FOLLOW(T)加入导FOLLOW(T’)中

由于ε∈FIRST(T’)，由步骤3的第二种情况，FOLLOW T的还能FOLLOW F

同时T→FT’还符合步骤2

即FIRST(T’)中的非空符号都能FOLLOW F
没有变化

再检查第4个产生式：T’→*FT’|ε
由算法的2，3步发现没有变化。

再检查第5个产生式：F→(E)| i
根据算法第二大步

也没有任何变化

由于第二遍FOLLOW集合发生变化，因此还需检查第三遍

发现第三遍没有变化，FOLLOW集合生成结束。

4.4 递归下降分析分析程序构造

构造不带回溯的自上而下分析程序

• 要消除文法的左递归性
• 克服回溯

• 构造不带回溯的自上而下分析器
• 分析程序由一组递归过程组成，文法中每个非终结符对应一个过程；所以这样的分析程序称为递归下降分析器。(因为文法的定义通常是递归的)

定义全局过程和变量：

• ADVANCE，把输入串指示器IP指向下一个输入符号，即读入一个单字符号
• SYM，IP当前所指的输入符号
• ERROR，出错处理子程序
  

看当前所指的输入符号是不是在FIRST(TE’)中

• 如果当前所指的输入符号是在FIRST(TE’)中

选择TE’这个候选去扩展A 选择这个候选去扩展A，相当于调用非终结符T所对应的子程序T去完成前一部分输入串的匹配推导。
当T匹配扩展完了后，调用非终结符E’所对应的子程序E’去完成后续输入串的匹配推导

当T,E’都扩展匹配完了后，A就识别完了

如果当前所指的输入符号不是在FIRST(TE’)中，则判断当前单词是不是在FIRST(BC)中,

• 如果当前所指的输入符号是在FIRST(BC)中

选择BC这个候选去扩展A，相应的推导/识别就通过调用语法单位B,C所对应的子程序来完成语法单位B,C的匹配。如果B,C匹配成功，A的匹配完毕。

如果当前单词既不在FIRST(TE’)中，也不在FIRST(BC)中，那我们是不是该选择ε呢？

按照LL(1)分析思路，应该首先判断当前的单词符号是不是在FOLLOW(A)中

• 如果当前的单词符号是不是在FOLLOW(A)中

即可以把A替换成ε，选择ε去扩展A相当于什么都不做。

• 如果当前单词既不在FIRST(TE’)中，也不在FIRST(BC)中，也不在FOLLOW(A)中，就应该报错。

文法的另一种表示法和转换图

扩充的巴科斯范式

引入上述元符号的文法亦称扩充的巴科斯范式

语法图

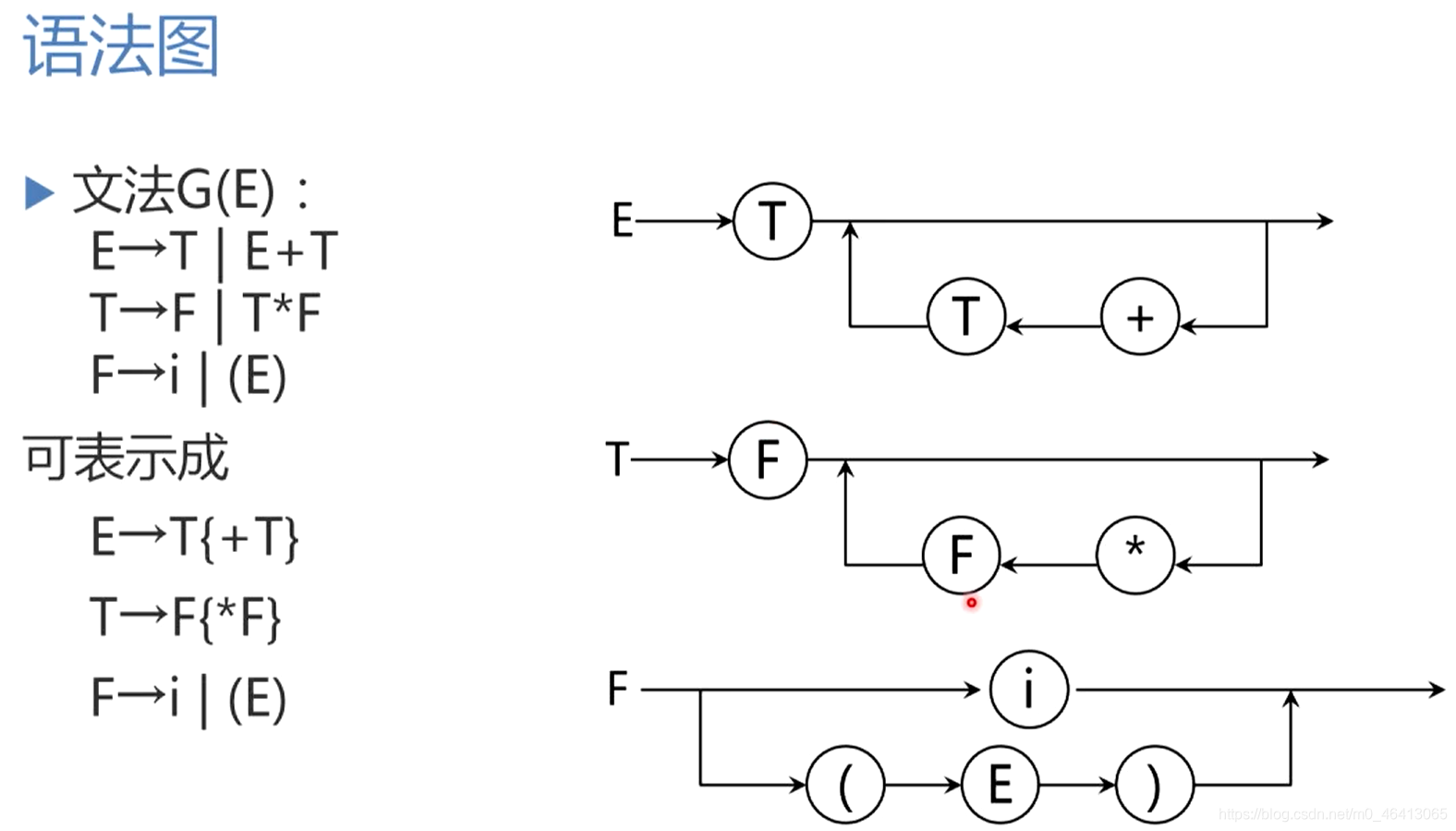
用巴科斯范式来描述文法对于实现递归下降程序非常方便。

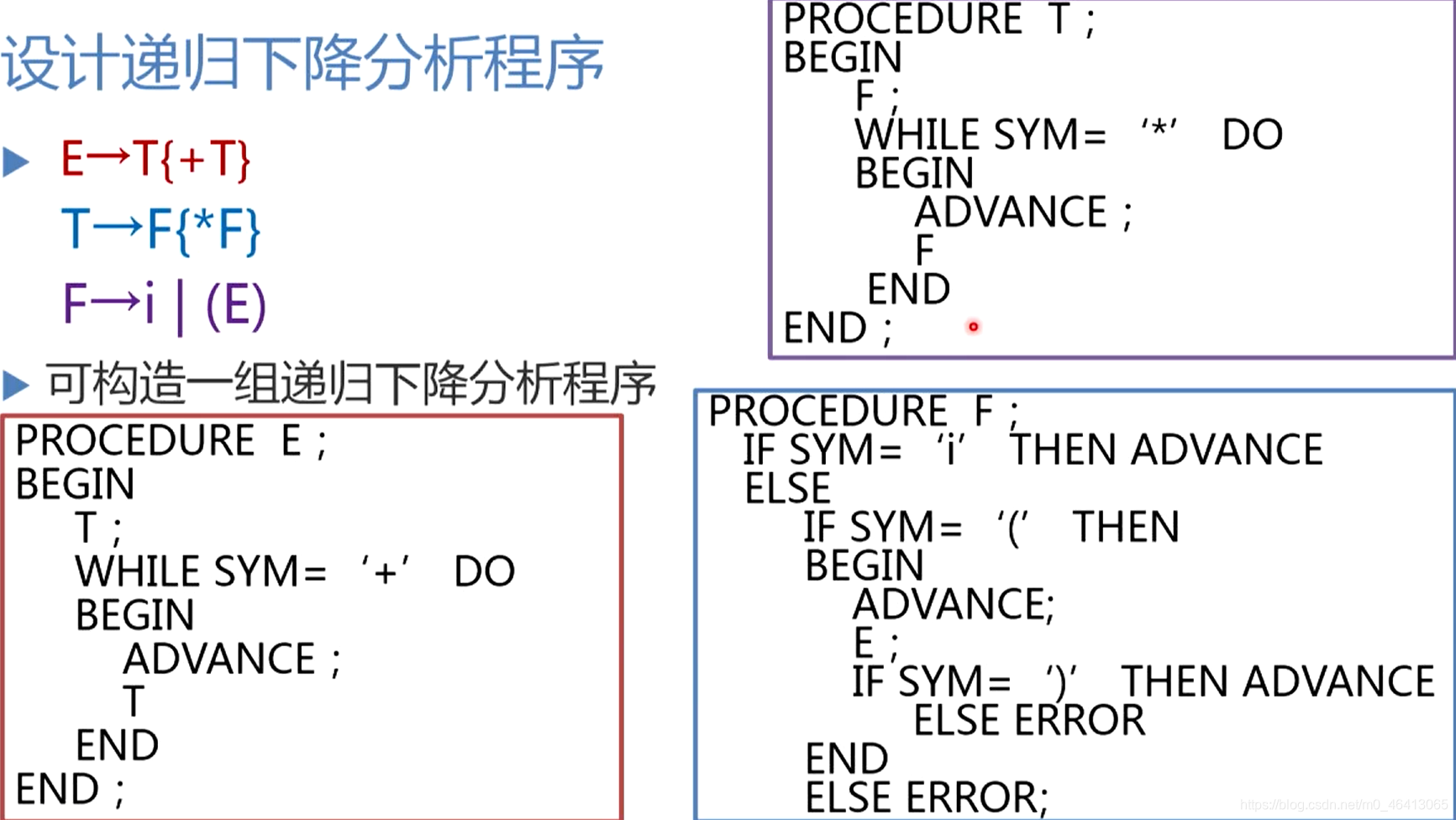
4.5 预测分析程序

预测分析程序工作原理

预测分析程序或LL(1)分析法：

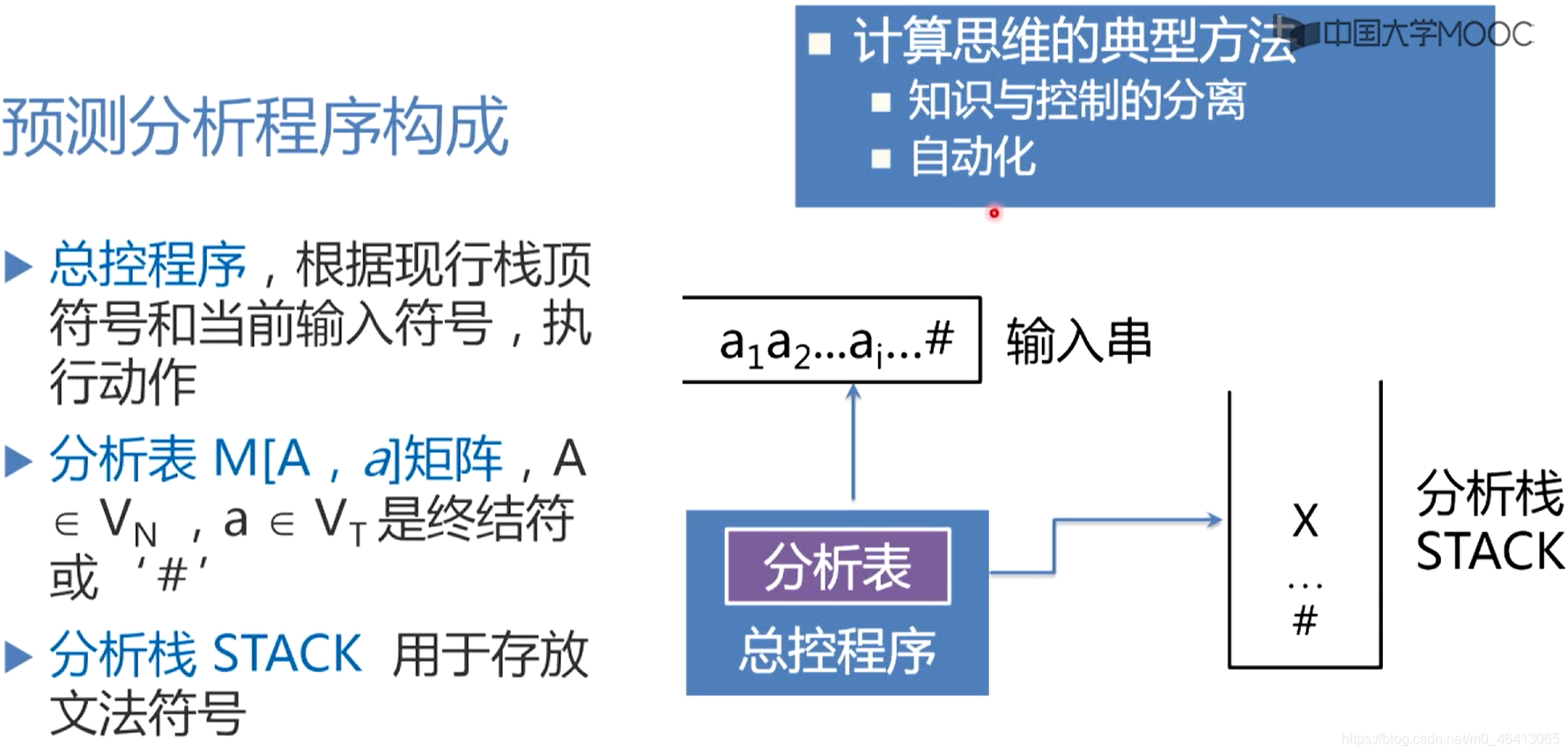
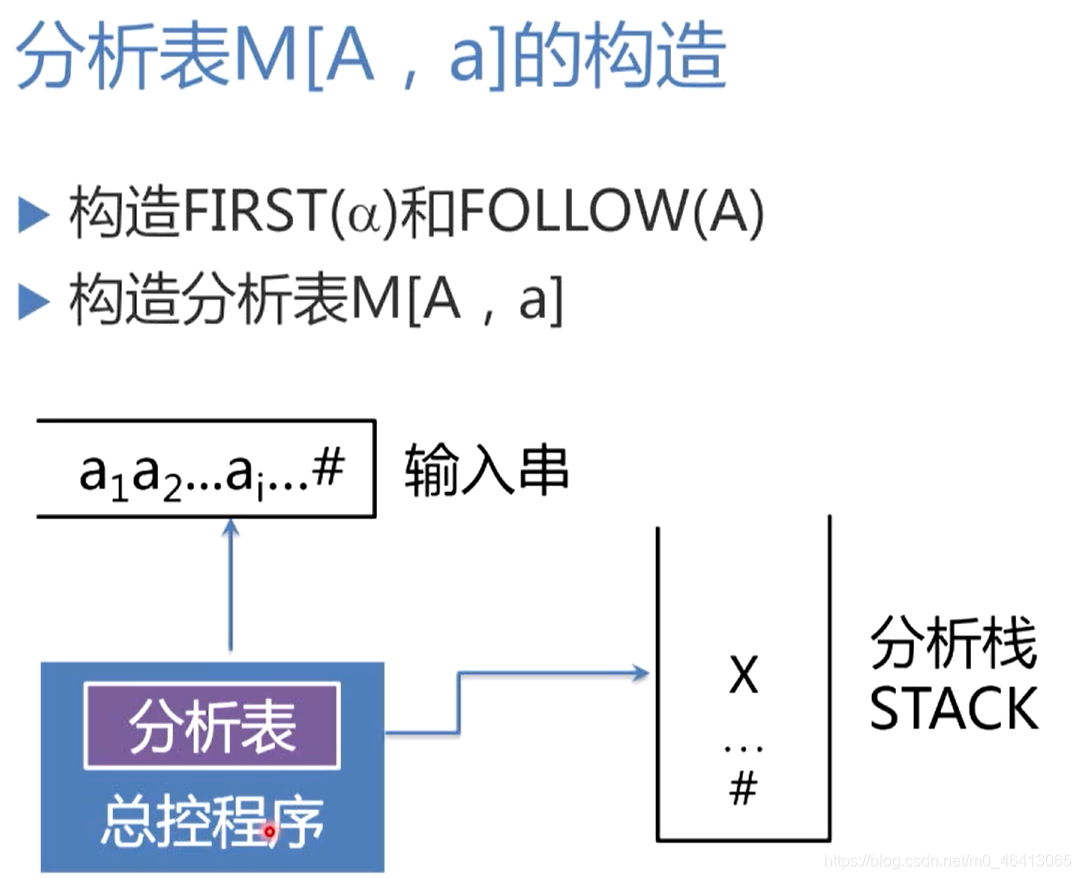
总控程序
通用的控制功能，总是根据现行栈顶符号和当前输入符号，查找分析表，执行分析表指定的动作。

分析表
是一个二维矩阵，也称为预测分析表，负责指导分析程序如何对栈顶符号进行操作，特别是指导分析程序面临栈顶符号是非终结符的时候，预测/选择非终结符是哪个候选，对它进行扩展。分析表是一个具有指导分析能力的数据结构。

它是个二维矩阵，第一维下标是文法的非终结符，第二维的下标是文法的终结符（句末符#也看成一个特殊的终结符），而二维矩阵的元素指明了当栈顶是非终结符A，面临输入符号是终结符a时，应该执行什么动作，用哪个候选进行扩展，如果是进行扩展的话，分析程序就会把这个候选压到栈里面，替换原来的非终结符，也就是说把栈顶的非终结符替换为它的候选，所以说总控程序总是根据现行栈顶的符号和当前的输入符号，来操作分析栈STACK

分析栈 STACK 用于存放需要匹配的文法符号，注意，栈的底部有一个文法符号，表示栈的底，输入串的最后，有一个#代边输入串的结束

注意，所有与语法相关的知识都在分析表中，控制程序/总控程序对不同的语法分析程序来说都是通用的

预测分析过程

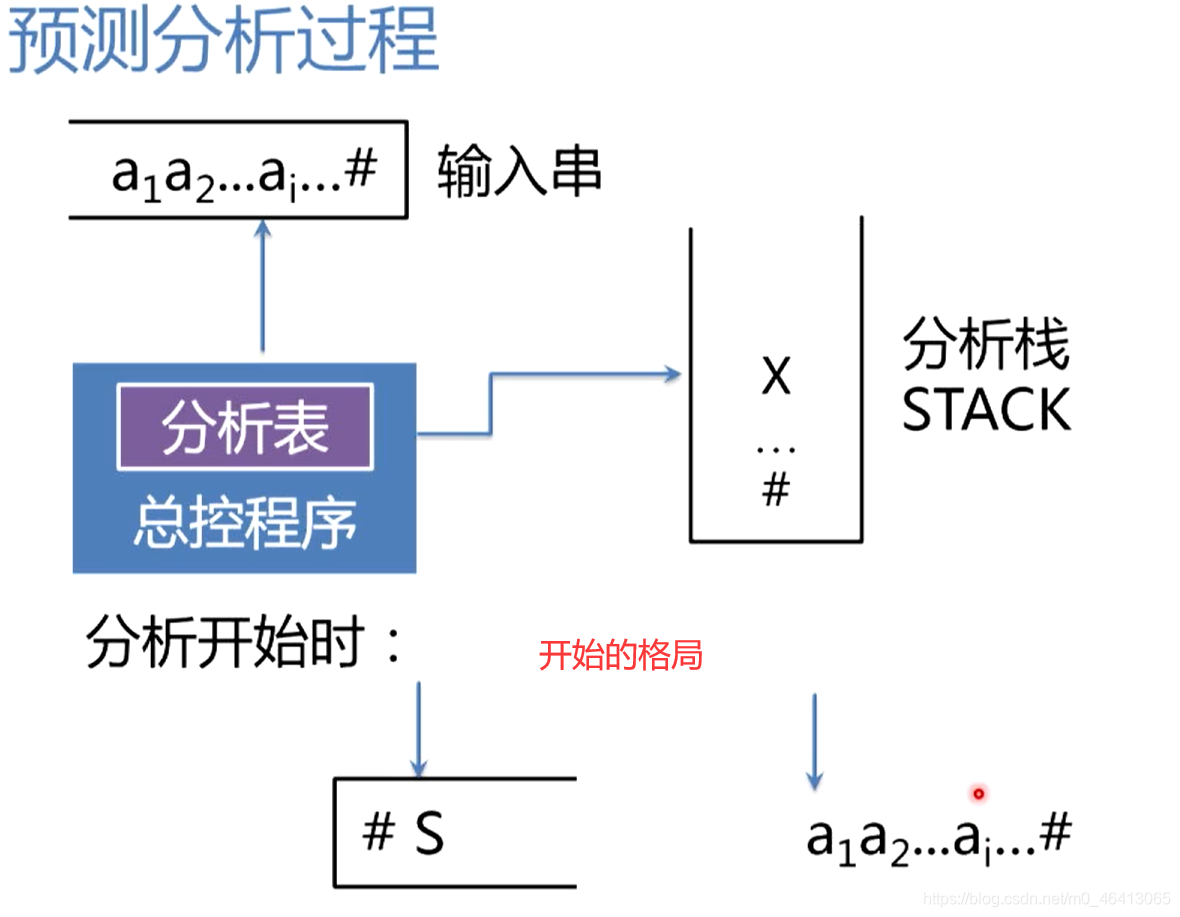
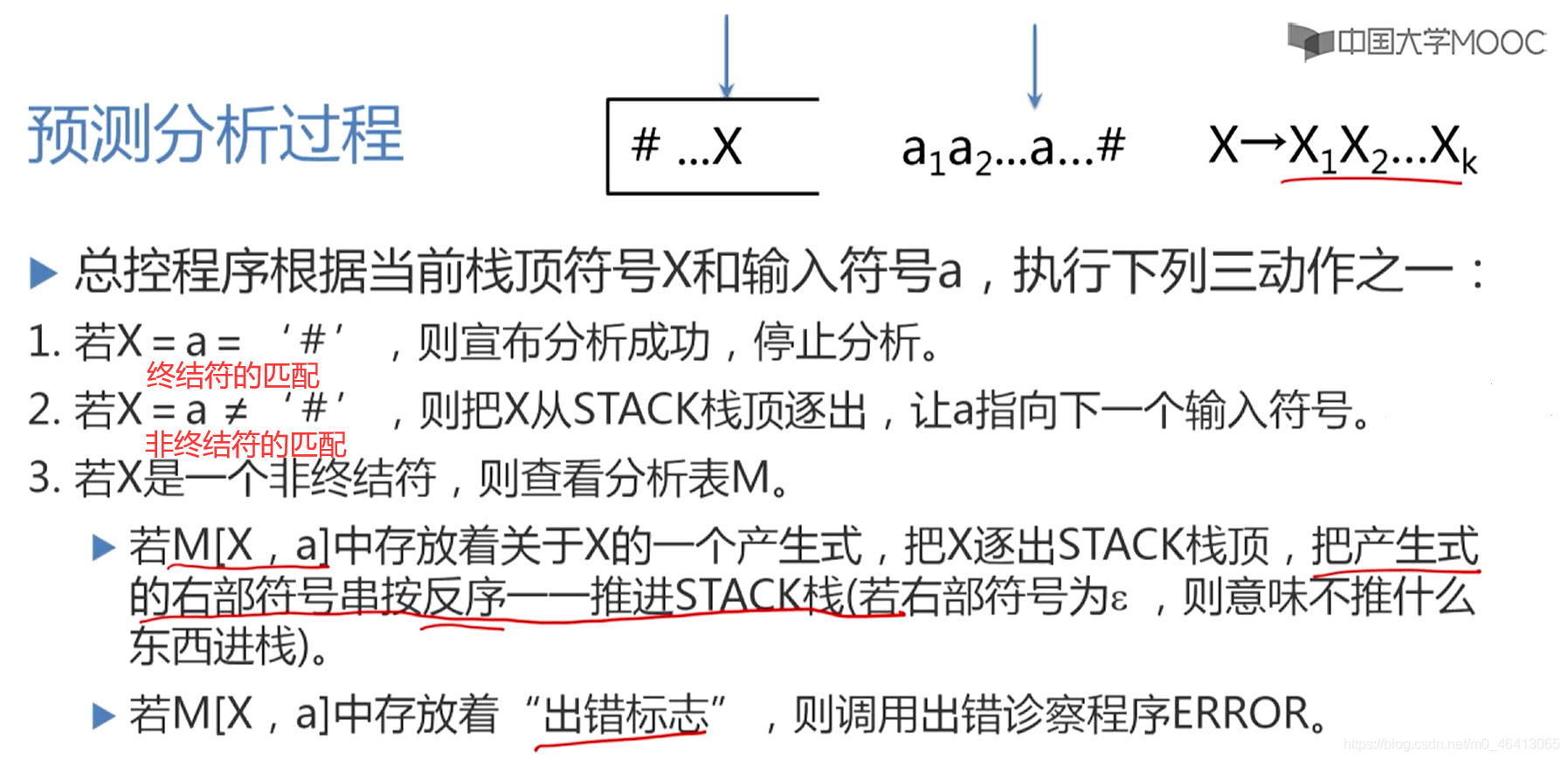
总控程序的基本实现

预测分析示例

看分析表，第一维的下标为非终结符，
第二维的下标都是终结符
每个格子里面要么是产生式，要么为空(意味着放的是出错标志)
同一行放的是同一个非终结符的定义
（关于它的第一维下标的终结符的定义式）

通过四元组描述每一步分析过程变化：

预测分析表的生成

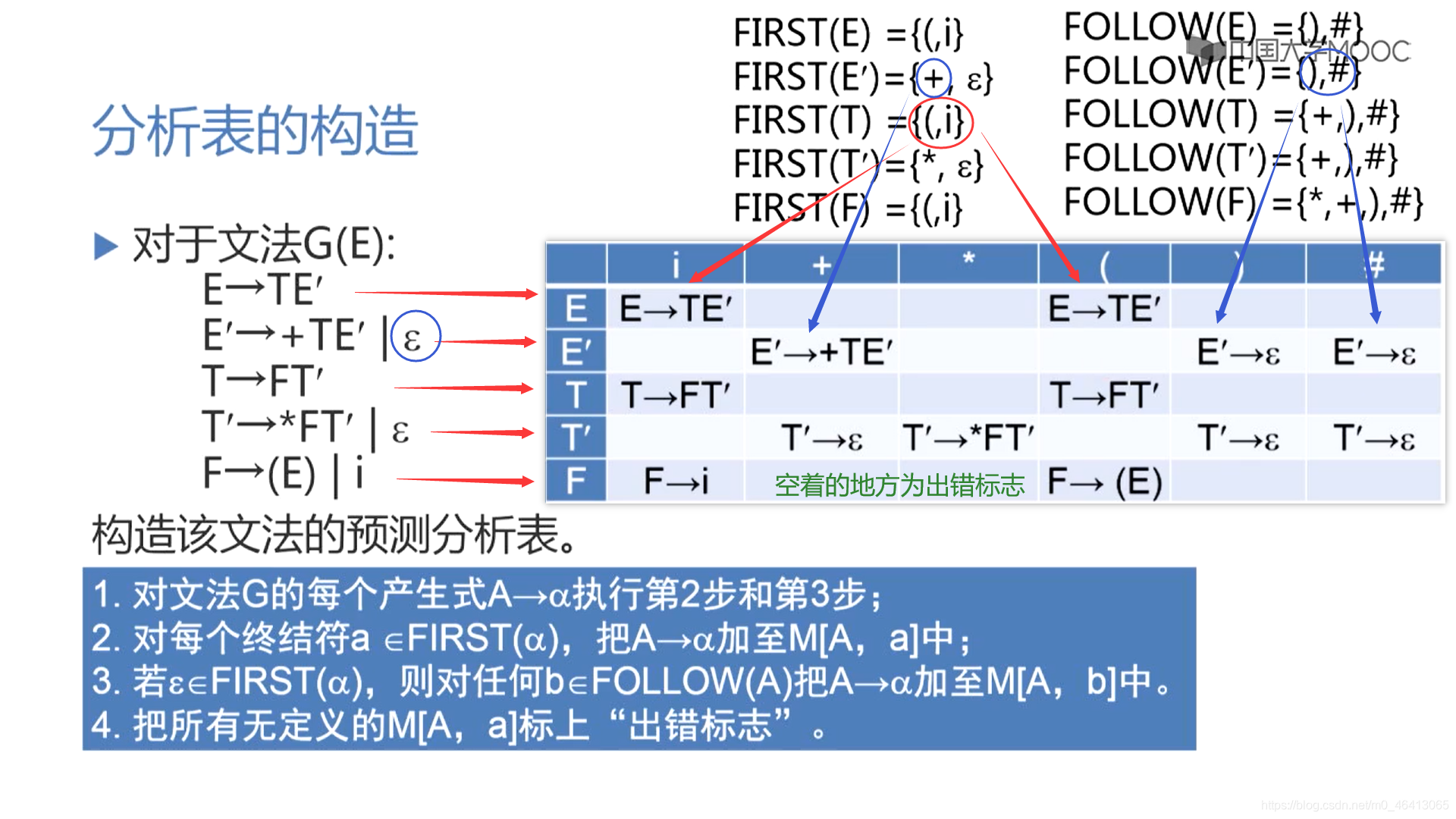
LL(1)文法与二义性