[数学]二维对数正态分布的概率分布，期望，方差和相关系数_子鱼inf_lyceum的博客

最近遇到了一个联合对数正态分布的相关系数的问题，搜遍全网无果，索性自己动手。本文借鉴了这个知乎回答

首先我们有二维正态分布：
X , Y ∼ B V N ( μ x , μ y , σ x 2 , σ y 2 , ρ x y ) X,Y\sim \mathbf{BVN}(\mu_x,\mu_y,\sigma_x^2,\sigma_y^2,\rho_{xy}) X,Y∼BVN(μx​,μy​,σx2​,σy2​,ρxy​)

取对数之后我们会得到二维对数正态分布的概率密度函数。只写了第一象限的函数表达式，其他地方都是0。
f ( x , y ) = 1 2 π 1 − ρ x y 2 σ x σ y x y exp ⁡ [ − 1 2 ( 1 − ρ x y 2 ) ( ( ln ⁡ x − μ x ) 2 σ x 2 − 2 ρ x y ( ln ⁡ x − μ x ) ( ln ⁡ y − μ y ) σ x σ y + ( ln ⁡ y − μ y ) 2 σ y 2 ) ] f(x,y)=\frac{1}{2\pi \sqrt{1-\rho_{xy}^2}\sigma_x\sigma_y xy}\exp \left[\frac{-1}{2(1 - \rho_{xy}^2)}\left(\frac{(\ln x-\mu_x)^2}{\sigma_x^2}-\frac{2\rho_{xy}(\ln x-\mu_x)(\ln y-\mu_y)}{\sigma_x\sigma_y}+\frac{(\ln y-\mu_y)^2}{\sigma_y^2}\right)\right] f(x,y)=2π1−ρxy2​ ​σx​σy​xy1​exp[2(1−ρxy2​)−1​(σx2​(lnx−μx​)2​−σx​σy​2ρxy​(lnx−μx​)(lny−μy​)​+σy2​(lny−μy​)2​)]

引用链接里有边缘分布（一维情况下）的期望和方差的推导过程，这里只写结论：
E ( X ) = exp ⁡ ( μ x + σ x 2 2 ) D ( X ) = exp ⁡ ( 2 μ x + σ x 2 ) ( exp ⁡ ( σ x 2 ) − 1 ) E(X)=\exp(\mu_x+\frac{\sigma_x^2}{2}) \\ D(X)=\exp(2\mu_x+\sigma_x^2)(\exp(\sigma_x^2)-1) E(X)=exp(μx​+2σx2​​)D(X)=exp(2μx​+σx2​)(exp(σx2​)−1)

接下来想算相关系数。首先我们有相关系数的公式：
ρ = C O V ( X , Y ) D ( X ) D ( Y ) = E ( X Y ) − E ( X ) E ( Y ) D ( X ) D ( Y ) \rho=\frac{COV(X,Y)}{\sqrt{D(X)D(Y)}}=\frac{E(XY)-E(X)E(Y)}{\sqrt{D(X)D(Y)}} ρ=D(X)D(Y) ​COV(X,Y)​=D(X)D(Y) ​E(XY)−E(X)E(Y)​

关键一步是计算 E ( X Y ) E(XY) E(XY)
E ( X Y ) = ∫ − ∞ + ∞ ∫ − ∞ + ∞ x y f ( x , y ) d x d y E(XY) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}xyf(x,y)\mathbf{d}x\mathbf{d}y E(XY)=∫−∞+∞​∫−∞+∞​xyf(x,y)dxdy

代入 f ( x , y ) f(x,y) f(x,y)
E ( X Y ) = ∫ 0 + ∞ ∫ 0 + ∞ 1 2 π 1 − ρ x y 2 σ x σ y exp ⁡ [ − 1 2 ( 1 − ρ x y 2 ) ( ( ln ⁡ x − μ x ) 2 σ x 2 − 2 ρ x y ( ln ⁡ x − μ x ) ( ln ⁡ y − μ y ) σ x σ y + ( ln ⁡ y − μ y ) 2 σ y 2 ) ] d x d y E(XY) = \int_{0}^{+\infty}\int_{0}^{+\infty}\frac{1}{2\pi \sqrt{1-\rho_{xy}^2}\sigma_x\sigma_y}\exp \left[\frac{-1}{2(1 - \rho_{xy}^2)}\left(\frac{(\ln x-\mu_x)^2}{\sigma_x^2}-\frac{2\rho_{xy}(\ln x-\mu_x)(\ln y-\mu_y)}{\sigma_x\sigma_y}+\frac{(\ln y-\mu_y)^2}{\sigma_y^2}\right)\right]\mathbf{d}x\mathbf{d}y E(XY)=∫0+∞​∫0+∞​2π1−ρxy2​ ​σx​σy​1​exp[2(1−ρxy2​)−1​(σx2​(lnx−μx​)2​−σx​σy​2ρxy​(lnx−μx​)(lny−μy​)​+σy2​(lny−μy​)2​)]dxdy

作变换（下面做了三步变换，只是处于计算直觉上的方便，其实完全可以只用一步。）
t x = ln ⁡ ( x ) − μ x 2 ( 1 − ρ x y 2 ) σ x , t y = ln ⁡ ( y ) − μ y 2 ( 1 − ρ x y 2 ) σ y t_x=\frac{\ln(x)-\mu_x}{\sqrt{2(1-\rho_{xy}^2)}\sigma_x},\quad t_y=\frac{\ln(y)-\mu_y}{\sqrt{2(1-\rho_{xy}^2)}\sigma_y} tx​=2(1−ρxy2​) ​σx​ln(x)−μx​​,ty​=2(1−ρxy2​) ​σy​ln(y)−μy​​

逆变换及其微分（由于对称只写x）
x = e 2 ( 1 − ρ x y 2 ) σ x t x + μ x , d x = 2 ( 1 − ρ x y 2 ) σ x e 2 ( 1 − ρ x y 2 ) σ x t x + μ x d t x x=e^{\sqrt{2(1-\rho_{xy}^2)}\sigma_x t_x+\mu_x},\quad \mathbf{d}x=\sqrt{2(1-\rho_{xy}^2)}\sigma_xe^{\sqrt{2(1-\rho_{xy}^2)}\sigma_x t_x+\mu_x}\mathbf{d}t_x x=e2(1−ρxy2​) ​σx​tx​+μx​,dx=2(1−ρxy2​) ​σx​e2(1−ρxy2​) ​σx​tx​+μx​dtx​

代入 E ( X Y ) E(XY) E(XY)得（节省空间不写积分上下限了）
E ( X Y ) = 1 π ∬ exp ⁡ [ − ( t x 2 − 2 ρ x y t x t y + t y 2 ) + 2 ( 1 − ρ x y 2 ) σ x t x + 2 ( 1 − ρ x y 2 ) σ y t y + μ x + μ y ] d t x d t y E(XY) = \frac{1}{\pi}\iint \exp \left[-\left( t_x^2-2\rho_{xy}t_xt_y+t_y^2\right)+\sqrt{2(1-\rho_{xy}^2)}\sigma_x t_x+\sqrt{2(1-\rho_{xy}^2)}\sigma_y t_y+\mu_x+\mu_y\right]\mathbf{d}t_x\mathbf{d}t_y E(XY)=π1​∬exp[−(tx2​−2ρxy​tx​ty​+ty2​)+2(1−ρxy2​) ​σx​tx​+2(1−ρxy2​) ​σy​ty​+μx​+μy​]dtx​dty​

提出含 μ \mu μ的常数项后，考虑指数上的二元多项式 t x 2 − 2 ρ x y t x t y + t y 2 − 2 ( 1 − ρ x y 2 ) σ x t x − 2 ( 1 − ρ x y 2 ) σ y t y t_x^2-2\rho_{xy}t_xt_y+t_y^2-\sqrt{2(1-\rho_{xy}^2)}\sigma_x t_x-\sqrt{2(1-\rho_{xy}^2)}\sigma_y t_y tx2​−2ρxy​tx​ty​+ty2​−2(1−ρxy2​) ​σx​tx​−2(1−ρxy2​) ​σy​ty​

利用沿轴平移来消掉一次项（步骤略，直接写变换）
u = t x − ρ x y σ y + σ x 2 ( 1 − ρ x y 2 ) , v = t y − ρ x y σ x + σ y 2 ( 1 − ρ x y 2 ) u=t_x-\frac{\rho_{xy}\sigma_y+\sigma_x}{\sqrt{2(1-\rho_{xy}^2)}},\quad v=t_y-\frac{\rho_{xy}\sigma_x+\sigma_y}{\sqrt{2(1-\rho_{xy}^2)}} u=tx​−2(1−ρxy2​) ​ρxy​σy​+σx​​,v=ty​−2(1−ρxy2​) ​ρxy​σx​+σy​​

原多项式变成了 u 2 − 2 ρ x y u v + v 2 − 1 2 ( σ x 2 + 2 ρ x y σ x σ y + σ y 2 ) u^2-2\rho_{xy}uv+v^2-\frac{1}{2}(\sigma_x^2+2\rho_{xy}\sigma_x\sigma_y+\sigma_y^2) u2−2ρxy​uv+v2−21​(σx2​+2ρxy​σx​σy​+σy2​)

提出原积分中的常数项，我们得到
E ( X Y ) = 1 π exp ⁡ ( μ x + μ y + 1 2 ( σ x 2 + 2 ρ x y σ x σ y + σ y 2 ) ) ∬ exp ⁡ [ − u 2 + 2 ρ x y u v − v 2 ] d u d v E(XY) = \frac{1}{\pi}\exp(\mu_x+\mu_y+\frac{1}{2}(\sigma_x^2+2\rho_{xy}\sigma_x\sigma_y+\sigma_y^2))\iint \exp \left[-u^2+2\rho_{xy}uv-v^2\right]\mathbf{d}u\mathbf{d}v E(XY)=π1​exp(μx​+μy​+21​(σx2​+2ρxy​σx​σy​+σy2​))∬exp[−u2+2ρxy​uv−v2]dudv

再对 u u u， v v v做一个伸缩变换，把积分函数配成正态分布形式
u ′ = 2 ( 1 − ρ x y 2 ) u , v ′ = 2 ( 1 − ρ x y 2 ) v u'=\sqrt{2(1-\rho_{xy}^2)}u,\quad v'=\sqrt{2(1-\rho_{xy}^2)}v u′=2(1−ρxy2​) ​u,v′=2(1−ρxy2​) ​v

于是得到
E ( X Y ) = exp ⁡ ( μ x + μ y + 1 2 ( σ x 2 + 2 ρ x y σ x σ y + σ y 2 ) ) 1 2 π ( 1 − ρ x y 2 ) ∬ exp ⁡ [ − 1 2 ( 1 − ρ x y 2 ) ( u 2 − 2 ρ x y u v + v 2 ) ] d u d v E(XY) =\exp(\mu_x+\mu_y+\frac{1}{2}(\sigma_x^2+2\rho_{xy}\sigma_x\sigma_y+\sigma_y^2)) \frac{1}{2\pi(1-\rho_{xy}^2)}\iint \exp \left[\frac{-1}{2(1-\rho_{xy}^2)}(u^2-2\rho_{xy}uv+v^2)\right]\mathbf{d}u\mathbf{d}v E(XY)=exp(μx​+μy​+21​(σx2​+2ρxy​σx​σy​+σy2​))2π(1−ρxy2​)1​∬exp[2(1−ρxy2​)−1​(u2−2ρxy​uv+v2)]dudv

指数项右边是一个正态分布概率密度的积分，因此等于1，于是得到了一个很简单的形式
E ( X Y ) = exp ⁡ ( μ x + μ y + 1 2 ( σ x 2 + 2 ρ x y σ x σ y + σ y 2 ) ) E(XY) = \exp(\mu_x+\mu_y+\frac{1}{2}(\sigma_x^2+2\rho_{xy}\sigma_x\sigma_y+\sigma_y^2)) E(XY)=exp(μx​+μy​+21​(σx2​+2ρxy​σx​σy​+σy2​))

然后我们把 E ( X Y ) E(XY) E(XY)， E ( X ) E(X) E(X)， E ( Y ) E(Y) E(Y)， D ( X ) D(X) D(X)， D ( Y ) D(Y) D(Y)代入相关系数公式化简得

ρ = exp ⁡ ( ρ x y σ x σ y ) − 1 ( exp ⁡ ( σ x 2 ) − 1 ) ( exp ⁡ ( σ y 2 ) − 1 ) \rho=\frac{\exp \left(\rho_{xy}\sigma_x\sigma_y \right)-1}{\sqrt{(\exp(\sigma_x^2)-1)(\exp(\sigma_y^2)-1)}} ρ=(exp(σx2​)−1)(exp(σy2​)−1) ​exp(ρxy​σx​σy​)−1​

但是这个相关系数的结果有个很奇怪的性质，困扰了我一天，那就是当 σ x ≠ σ y \sigma_x\neq \sigma_y σx​​=σy​的时候 ρ \rho ρ取不到 [ − 1 , 1 ] [-1,1] [−1,1]，我用数字帝国画了个 σ x = 1 ， σ y = 2 \sigma_x=1，\sigma_y=2 σx​=1，σy​=2时的草图，长这样：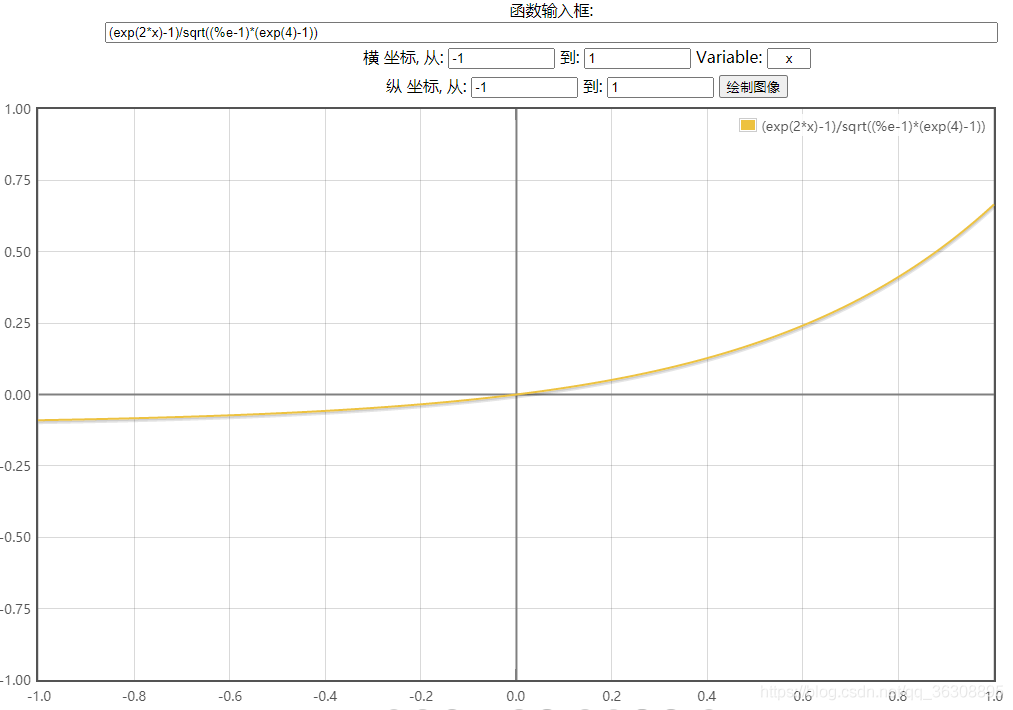
然后就怀疑我哪里做错了，后来想着还是拿matlab数值计算一下。代码如下：

rho = 0.99;
sigma_x = 2;
sigma_y = 1;
mu_x = 1;
mu_y = 1;
%ff = @(x,y)(exp(-((((log(x)-mu_x).^2./sigma_x.^2)-(2.*rho.*(log(x)-mu_x).*(log(y)-mu_y)./(sigma_x.*sigma_y))+((log(y)-mu_y).^2)./sigma_y.^2)./(2.*(1-rho.^2))))./(2*sigma_x*sigma_y.*pi.*sqrt(1-rho.^2).*x.*y));原始函数
fexy = @(x, y)(exp(-((((log(x)-mu_x).^2./sigma_x.^2)-(2.*rho.*(log(x)-mu_x).*(log(y)-mu_y)./(sigma_x.*sigma_y))+((log(y)-mu_y).^2)./sigma_y.^2)./(2.*(1-rho.^2))))./(2*sigma_x*sigma_y.*pi.*sqrt(1-rho.^2)));
exy = integral2(fexy,0,inf,0,inf,'Method','iterated','AbsTol',0,'RelTol',1e-10);
exey = exp(mu_x+mu_y+sigma_x^2/2+sigma_y^2/2);
corr = (exy-exey)/(exey*sqrt((exp(sigma_x^2)-1)*(exp(sigma_y^2)-1)));

结果是0.6505，和图像相符，也就是说二维对数正态分布的相关系数取值范围确实不总是 [ − 1 , 1 ] [-1,1] [−1,1]。
再附一个画二维正态和二维对数正态概率分布的代码：

X1=[0.01:0.01:3];
Y1=[0.01:0.01:3];
[x,y]=meshgrid(X1,Y1);
rho = 0.5;
sigma_x = 1;
sigma_y = 1;
mu_x = 1;
mu_y = 1;
BVLN=(exp(-((((log(x)-mu_x).^2./sigma_x.^2)-(2.*rho.*(log(x)-mu_x).*(log(y)-mu_y)./(sigma_x.*sigma_y))+((log(y)-mu_y).^2)./sigma_y.^2)./(2.*(1-rho.^2))))./(2*sigma_x*sigma_y.*pi.*sqrt(1-rho.^2).*x.*y));
BVN=(exp(-((((x-mu_x).^2./sigma_x.^2)-(2.*rho.*(x-mu_x).*(y-mu_y)./(sigma_x.*sigma_y))+((y-mu_y).^2)./sigma_y.^2)./(2.*(1-rho.^2))))./(2*sigma_x*sigma_y.*pi.*sqrt(1-rho.^2)));
subplot(1,2,1);surf(x,y,BVLN);
subplot(1,2,2);surf(x,y,BVN);

画出来是这种感觉：

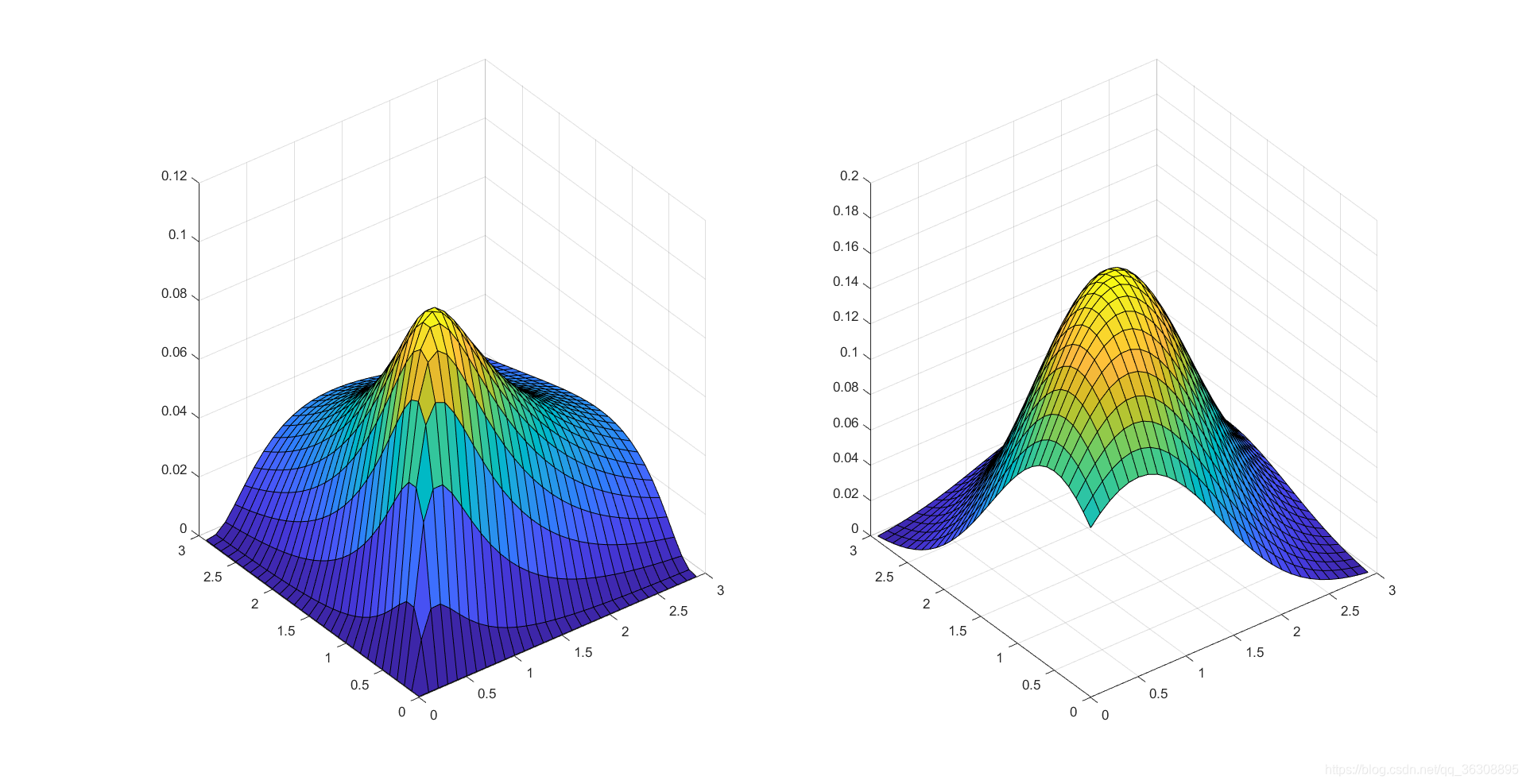
断断续续算了四天（主要是开始时不知道如何做变换），算的心态爆炸，给个免费的赞再走吧。