目录
0 专栏介绍1 线段与线段相交检测2 线段与圆相交检测3 线段与矩形相交检测4 算法仿真与可视化4.1 核心算法4.2 仿真实验
0 专栏介绍
?课设、毕设、创新竞赛必备!?本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
?详情:运动规划实战进阶:轨迹优化篇
本期实现如下的碰撞检测效果
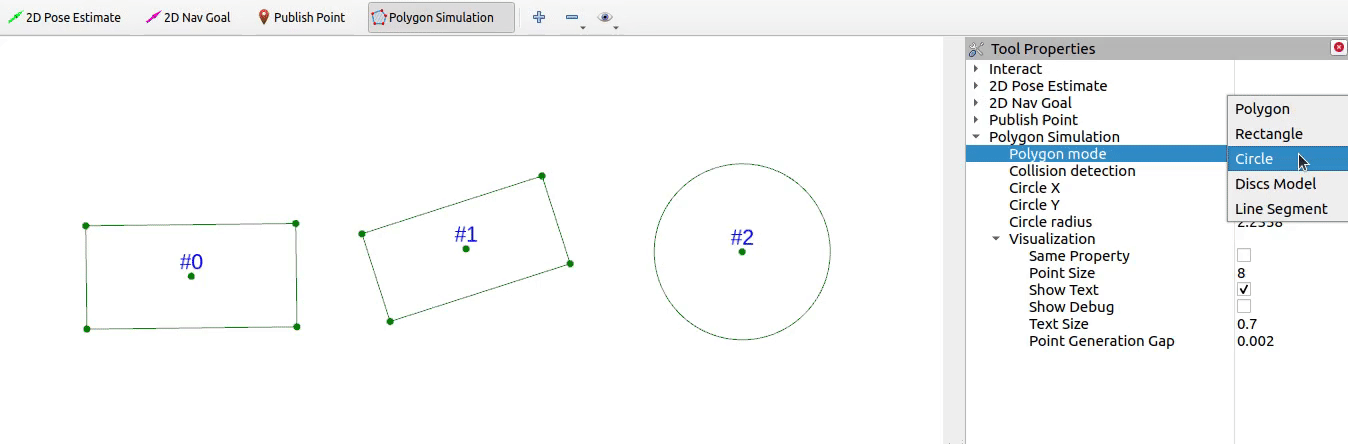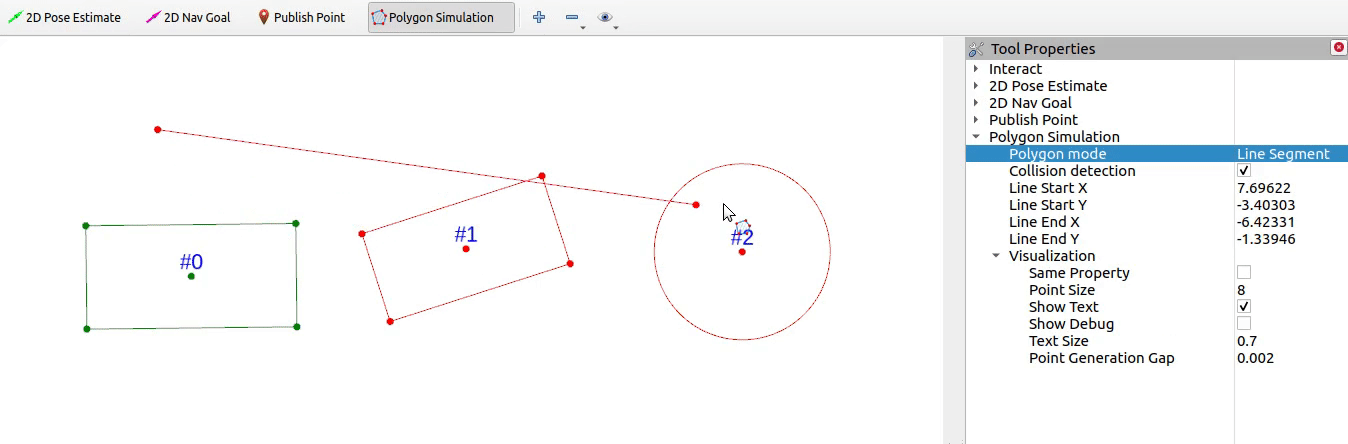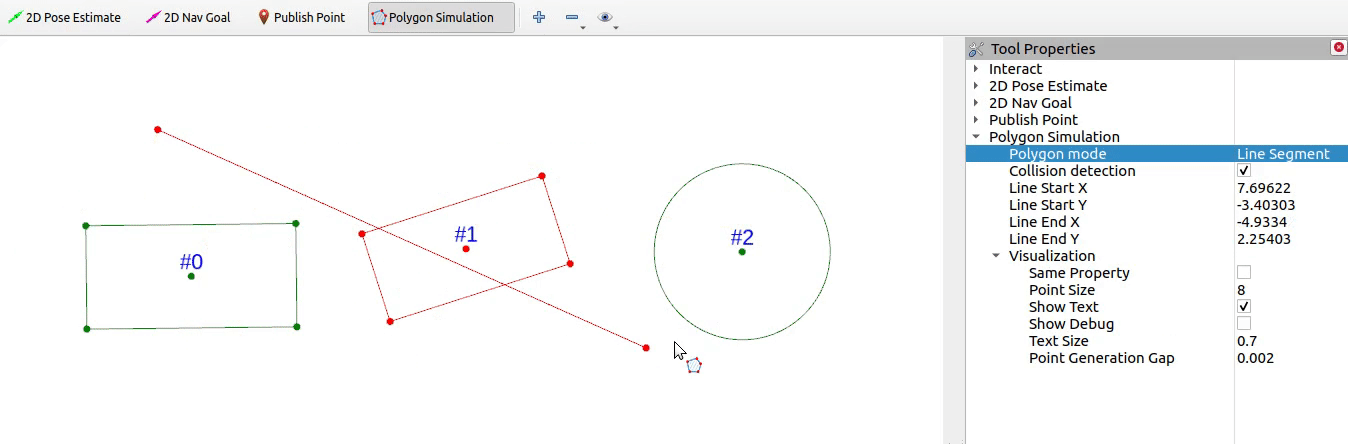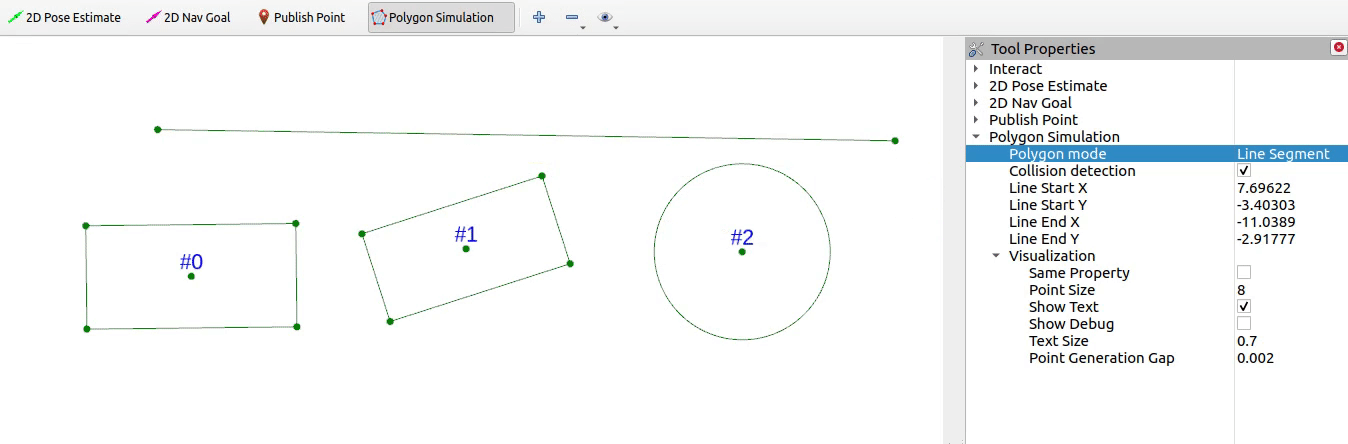
1 线段与线段相交检测
线段相交检测是广义多边形计算几何的基础,一般分为两个步骤:快速排斥与跨立实验
快速排斥
如图所示,快速排斥通过检测两条线段对应的轴对齐包围盒来快速检测潜在的相交可能性,如果两个AABB不重叠,则表明一定不相交,否则需要进一步进行跨立实验
跨立实验
跨立实验通过向量积运算判断线段的跨立性:设两条线段的起始点分别为 s 1 \boldsymbol{s}_1 s1、 e 1 \boldsymbol{e}_1 e1和 s 2 \boldsymbol{s}_2 s2、 e 2 \boldsymbol{e}_2 e2,选定其中一条线段 s 1 e 1 = e 1 − s 1 \boldsymbol{s}_1\boldsymbol{e}_1=\boldsymbol{e}_1-\boldsymbol{s}_1 s1e1=e1−s1和该线段端点与另一条线段的两个端点连成的向量 s 1 s 2 \boldsymbol{s}_1\boldsymbol{s}_2 s1s2、 s 1 e 2 \boldsymbol{s}_1\boldsymbol{e}_2 s1e2,若 ( s 1 e 1 × s 1 s 2 ) ⋅ ( s 1 e 1 × s 1 e 2 ) < 0 \left( \boldsymbol{s}_1\boldsymbol{e}_1\times \boldsymbol{s}_1\boldsymbol{s}_2 \right) \cdot \left( \boldsymbol{s}_1\boldsymbol{e}_1\times \boldsymbol{s}_1\boldsymbol{e}_2 \right) <0 (s1e1×s1s2)⋅(s1e1×s1e2)<0则表明另一条线段的两个端点分布在当前线段左右两侧,称线段 s 2 e 2 \boldsymbol{s}_2\boldsymbol{e}_2 s2e2跨立线段 s 1 e 1 \boldsymbol{s}_1\boldsymbol{e}_1 s1e1。当前仅当两条线段互相跨立时,线段相交
算法流程如下所示
2 线段与圆相交检测
如图所示,设线段参数方程为
x = s + t ⋅ ( e − s ) , t ∈ [ 0 , 1 ] \boldsymbol{x}=\boldsymbol{s}+t\cdot \left( \boldsymbol{e}-\boldsymbol{s} \right) , t\in \left[ 0,1 \right] x=s+t⋅(e−s),t∈[0,1]
圆的方程为
∥ x − c ∥ 2 = r 2 \left\| \boldsymbol{x}-\boldsymbol{c} \right\| ^2=r^2 ∥x−c∥2=r2
联立可得
∥ e − s ∥ 2 t 2 + 2 ( e − s ) T ( s − c ) t + ∥ s − c ∥ 2 − r 2 = 0 \left\| \boldsymbol{e}-\boldsymbol{s} \right\| ^2t^2+2\left( \boldsymbol{e}-\boldsymbol{s} \right) ^T\left( \boldsymbol{s}-\boldsymbol{c} \right) t+\left\| \boldsymbol{s}-\boldsymbol{c} \right\| ^2-r^2=0 ∥e−s∥2t2+2(e−s)T(s−c)t+∥s−c∥2−r2=0
该二次方程的判别式为 Δ \varDelta Δ,若 Δ < 0 \varDelta <0 Δ<0则一定不相交;若 Δ ⩾ 0 \varDelta \geqslant 0 Δ⩾0且 ∃ t ∈ [ 0 , 1 ] \exists t\in \left[ 0,1 \right] ∃t∈[0,1]则相交,其中区间限制保证了线段相交而非直线相交。
3 线段与矩形相交检测
线段与多边形是否相交可以简单地通过两两线段的相交检测判定,但对于矩形而言,可以特化为两步
若线段端点在矩形内部则一定相交;若线段与矩形对角线相交则一定相交。当上述两步都不相交时说明线段与矩形相离。步骤2与线段相交检测相同,这里仅介绍步骤1。
如图所示,对于轴对齐包围盒,仅需要对端点进行AABB碰撞检测即可;对于旋转包围盒,则按照圆-矩形碰撞检测的思路,将中心向量 v \boldsymbol{v} v绕矩形中心反向旋转 α \alpha α,再按AABB碰撞检测即可。可以参考:
碰撞检测 | 详解圆-矩形碰撞检测与N圆覆盖模型(附ROS C++可视化)碰撞检测 | 详解矩形AABB与OBB碰撞检测算法(附ROS C++可视化)4 算法仿真与可视化
4.1 核心算法
核心算法如下所示
线段与线段相交检测
bool VLineSegment::isLineIntersaction(const Ogre::Vector3& start, const Ogre::Vector3& end) const{ if (length_ <= kMathEpsilon || std::hypot(start.x - end.x, start.y - end.y) <= kMathEpsilon) return false; if (_endPointTest(start, end)) return true; if (!_rapidTest(start, end)) return false; if (_straddleTest(start, end)) return true; return false;}线段与圆相交检测
auto isCollisionWithCircle = [&](const Ogre::Vector3& center, const float radius) -> bool { if (std::hypot(center.x - start_.x, center.y - start_.y) < radius) return true; if (std::hypot(center.x - end_.x, center.y - end_.y) < radius) return true; const float a = innerProduct(end_ - start_, end_ - start_); const float b = 2 * innerProduct(end_ - start_, start_ - center); const float c = innerProduct(start_ - center, start_ - center) - radius * radius; const float delta = b * b - 4 * a * c; if (delta < kMathEpsilon) return false; const float t1 = (-b + std::sqrt(delta)) / (2 * a); const float t2 = (-b - std::sqrt(delta)) / (2 * a); if (isWithin(t1, 0.0f, 1.0f) || isWithin(t2, 0.0f, 1.0f)) return true; return false; }; auto other_circle = std::dynamic_pointer_cast<VCircle>(other); const auto& other_circle_center = other_circle->center(); const auto& other_circle_radius = other_circle->radius(); return isCollisionWithCircle(other_circle_center, other_circle_radius);线段与矩形相交检测
const auto other_rect = std::dynamic_pointer_cast<VRectangle>(other);const float cos_angle = other_rect->cos_angle();const float sin_angle = other_rect->sin_angle();const float cx = other_rect->center().x, cy = other_rect->center().y;const float half_l = 0.5f * std::fabs(other_rect->length()), half_w = 0.5f * std::fabs(other_rect->width());auto isPointInRect = [&](const Ogre::Vector3& pt) -> bool { const float pt2rect_x = pt.x - cx; const float pt2rect_y = pt.y - cy; const float rx = pt2rect_x * cos_angle + pt2rect_y * sin_angle + cx; const float ry = -pt2rect_x * sin_angle + pt2rect_y * cos_angle + cy; return (rx <= cx + half_l && rx >= cx - half_l && ry <= cy + half_w && ry >= cy - half_w);};if (isPointInRect(start_) || isPointInRect(end_)) return true;const float theta = -2 * std::atan(half_w / half_l);const auto lt_pt = other_rect->left_top_point();const auto rb_pt = 2 * other_rect->center() - lt_pt;const auto lt2center = lt_pt - other_rect->center();const Ogre::Vector3 lb_pt(lt2center.x * std::cos(theta) - lt2center.y * std::sin(theta) + cx, lt2center.x * std::sin(theta) + lt2center.y * std::cos(theta) + cy, 0.0f);const auto rt_pt = 2 * other_rect->center() - lb_pt;if (isLineIntersaction(lt_pt, rb_pt) || isLineIntersaction(rt_pt, lb_pt)) return true;return false;4.2 仿真实验
通过Rviz->Add New Tool添加Polygon Simulation插件
开启碰撞检测功能后,验证 N N N圆覆盖碰撞检测算法
线段与线段相交检测完整工程代码请联系下方博主名片获取
? 更多精彩专栏:
《ROS从入门到精通》《Pytorch深度学习实战》《机器学习强基计划》《运动规划实战精讲》…?源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系?