欢迎来到动物园!
在已有的众多的优化算法里,生物的行为是研究者们最常模仿的对象,所以你就会经常看到狼啊、麻雀啊、鲸鱼啊,甚至还有小龙虾。
当然这些算法的解决思路都很优秀,而对优化算法的应用和改进,也是写论文中极佳的创新点——能研究出新的优化算法固然最好;就算没有,单是将参数寻优加到你的主算法流程中,也可以算是可以说道说道的创新点之一了,在我们乏善可陈(并不)的论文中,也可以提一点亮色~
然而此时同学们可能就纠结了,究竟哪一种优化算法更好呢?又该怎样实现“无痛”编程呢?
一、为什么要用优化算法
我们在使用优化算法时,就像是在一个大山上寻宝。这座大山就是我们的搜索空间,山上的每一个位置对应着一组参数的取值。而山的高低起伏,则代表了不同参数组合下模型性能的好坏。我们的目标,就是在这座山上找到最高的峰,也就是最优的参数组合。但是山太大了,我们不可能把每个位置都走一遍。所以,我们就需要一些"小伙伴"来帮忙,它们就是优化算法中的"粒子"或"个体"。
一开始,我们让这些小伙伴随机地分散在山的各个位置。然后,它们各自开始向山顶进发。每走一步,小伙伴们就会比较一下当前位置的海拔高度,也就是适应度函数的大小。它们会记住自己走过的最高点,也会跟其他小伙伴交流各自的最高点。这样,大家就可以朝着最有希望的方向前进。

这个过程,就对应着优化算法中的"迭代"。每一轮迭代,都像是小伙伴们爬山的一步。迭代的次数,就是小伙伴们爬山的总步数。迭代越多,小伙伴们就爬得越高,找到山顶的机会也就越大。
当然,小伙伴们爬山也是有规则的。它们不能爬出我们规定的区域,这就是"参数边界"。
此外,小伙伴们的数量,也就是"种群数",也会影响寻宝的效率。种群数越多,搜索的范围就越广,但计算量也会增加。
优化算法的奥妙,就在于如何指挥这些小伙伴,让它们既能高效地寻找山顶,又不会陷入"陷阱"(局部最优)。不同的算法,就像是不同的领队,有不同的搜索策略。
归根究底,大多数寻优算法都是按照上边的思路实现的。
二、我们到底在“优化”什么
回到具体的学术问题上来,很多同学在提到想要对参数做寻优时,并不知道优化的目标是什么。
其实这要从你的研究的目的出发,这里句几个例子大家就明白了:
假设我们正在训练一个图像分类模型:那么模型在验证集上的准确率就是我们的优化目标;学习率、批量大小等这些超参数就是要优化的参数。我们希望找到一组超参数的组合,使得模型在验证集上的准确率最高。假设我们正在使用支持向量机(SVM)进行时间序列预测:模型在测试集上的MSE值就是我们的优化目标,而那些SVM的核函数的类型、惩罚系数C等参数就是要优化的参数。假设我们正在使用变分模态分解(VMD)来分析一个非平稳信号:VMD有一个重要的参数k,表示分解出的模态数。我们希望找到一个最优的k值,使得分解出的各个模态熵值之和最小。这里,熵值就可以作为我们的优化目标,而VMD的参数k就是要优化的参数。所以,寻优首先要明确你想要达到的目标,对于分类算法,目标是正确率最高;对于预测算法,目标是误差值最低——这是两类最常见的场景。这个目标还可以是收益率最高、熵值最低、路径最短等等不一而足。相信看到这儿,你应该知道你的优化目标是什么了。
但是需要强调的是,我们寻优有时候不仅仅要找到目标的极值,还要找到能够计算出该极值对应的参数数值,原因和结果有时候是同样重要的!
寻优通常就在超曲面寻找最大值或最小值
三、优化算法的几个重要组成概念
1.适应度函数
适应度函数是优化算法中最关键的部分之一。(甚至没有之一,因为优化策略我已经帮你们集成好了哈哈)
在前面的例子中,我们提到了一些常见的适应度函数,如准确率、误差等,这些函数都能够量化地反映出解的好坏。
不过需要注意的是,在实操层面,各种优化算法都是向最小值方向搜寻,所以“误差”可以直接作为适应度函数,因为我们一定是希望误差值越小越好;但对于分类算法,是需要将(1-准确率)作为适应度函数的,也即以“错误率”为适应度函数。
除此之外,还会有五花八门的适应度函数。不过只要你知道自己想要的是什么,设计一个合适的适应度函数就不是太大的难题。
2.参数边界值
参数边界值定义了优化搜索的范围。它告诉优化算法,每个参数允许取的最小值和最大值是多少。
设定合理的边界值可以大大缩小搜索空间,提高优化效率。如果边界设置得过宽,算法可能花费大量时间在无意义的区域搜索;如果边界设置得过窄,又可能错过最优解。
参数边界通常由我们对问题的先验知识来决定。
3.优化算法的“种群数”和迭代次数
"种群数"和迭代次数是两个关键的超参数,它们控制着优化算法的计算资源和时间。
"种群数"表示算法在每一轮迭代中维护的候选解的数量。种群数越大,算法的搜索能力越强,但计算开销也越大。当然,这里的“种群数”是笼统的说法,到具体优化算法中,可能指的是狼群数量、麻雀数量、小龙虾数量等等。
迭代次数表示算法运行的轮数。一般来说,迭代次数越多,算法得到的解就越接近最优。但是,迭代次数的增加也意味着计算时间的增长。
在实践中,我们需要根据问题的复杂度和可用的计算资源来权衡种群数和迭代次数。对于比较简单的问题,较小的种群和较少的迭代可能就足够了;但对于复杂的问题,我们可能需要增大这两个参数。
四、常用的优化算法
自20世纪50年代以来,研究者们提出了各种各样的优化算法,从经典的数学规划方法,到启发式的智能优化算法,再到借鉴自然界的生物启发算法,优化算法的发展历程可谓是丰富多彩。这里举几个例子让大家感受一下[1],详细的算法流程我就不展开一一讲了,因为大多还是比较好理解的。想深入了解的,参考论文我也都附在文末了:
1.灰狼优化算法

这种算法模拟了灰狼群体的社会等级制度和狩猎行为。在灰狼群体中,等级最高的是头狼(α),负责决策;其次是副头狼(β)和侍从狼(δ),协助头狼;等级最低的是奥米加狼(ω),服从其他狼的命令。在算法中,候选解被看作是一群灰狼,最优解对应α狼,次优解对应β狼和δ狼,其他解对应ω狼。算法通过模拟灰狼的围捕、攻击和搜索行为来更新解,不断逼近最优解。
2.鲸鱼优化算法

灵感来自座头鲸的独特捕食方式,座头鲸会潜入鱼群下方,吐出气泡形成一个螺旋状的气泡网,将鱼群围困其中,然后穿过气泡网捕食鱼群。鲸鱼算法通过模拟这种行为来搜索最优解。算法分为三个阶段:包围猎物、萃取攻击和搜索猎物。在包围阶段,鲸鱼会不断更新自己的位置,逼近最优解;在萃取攻击阶段,鲸鱼会沿着螺旋路径接近猎物;在搜索阶段,鲸鱼会随机搜索猎物。通过这三个阶段的迭代,算法最终找到最优解。
3.麻雀优化算法

这种算法模拟了麻雀群体的捕食、警戒和迁徙行为。在麻雀群体中,有一部分麻雀负责觅食(生产者),另一部分麻雀负责警戒(防御者)。当生产者找到食物时,会通过发出叫声来吸引其他麻雀;当防御者发现危险时,会通过发出警报来提醒其他麻雀。在算法中,候选解被看作是一群麻雀,分为生产者和防御者两类。算法通过模拟麻雀的觅食、警戒和迁徙行为来更新解。生产者负责探索新的区域,防御者负责在当前最优解附近搜索。通过生产者和防御者的协作,算法可以在探索和利用之间取得平衡,高效地找到最优解。
*剩余十三种优化算法概述及其参考文献我放到文末了。
五、MATLAB实现
网上的各类代码琳琅满目[1],但是大家在使用过程中就会面临一个问题:我想要试验不同的优化算法效果,可能还要做对比图,但是没更换一次优化算法,就需要重构整套代码的方方面面,一不小心就各种报错。
那有没有把各种优化算法集合成一条代码,只需要修改优化算法名称就能轻松使用不同类型算法的代码呢?
现在有了!它集合了总共16种优化算法(见附录介绍)。
使用这个代码,你需要做的基本只有替换你自己的适应度函数,剩下的都交给封装函数做就好了。
下面举个例子,我们将寻优的目标模型设置为这样一个二元二次方程:
% 定义目标函数fitness = (a-1)^2 + (b-2)^2;大家一眼就能看出来,fitness最小值对应的参数值为a=1,b=2。
下边我们交给程序:
%% 1.设置寻优相关参数dim = 2; % 优化参数的个数,这里设定为2,表示有两个需要寻优的参数lb = [-100,-100]; % 定义每个优化参数的取值下限,这里对两个参数都设置为-100ub = [100,100]; % 定义每个优化参数的取值上限,这里对两个参数都设置为100OAmethod = 'SSA'; % 选择使用的优化算法,这里使用'SSA'即麻雀搜索算法dataforFitness = []; % 这里可以定义需要传递给适应度函数的额外数据,由于本测试中不需要,因此留空pop = 300; % 设置优化算法的种群大小Max_iteration = 100; % 设置优化算法的最大迭代次数%% 2.调用优化算法函数,传入上述定义的参数% 返回最优位置Best_pos,最优适应度值Best_score,迭代过程的适应度曲线curve[Best_pos,Best_score,curve] = kOptimizationAlgorithm(OAmethod, dataforFitness, lb, ub, dim, pop, Max_iteration);核心算法就只有调用的最后一行代码,上边七行是必要的参数设置,其中主要参数在上边章节中我们都提到了。
此时运行代码,可以得到:
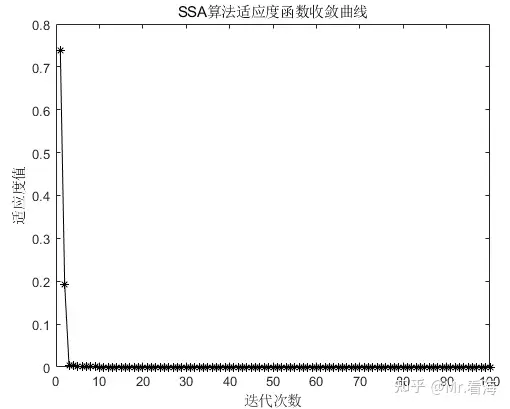
适应度函数收敛曲线
从上边的图中可以看出,寻优算法迅速将适应度函数的输出降到0附近,但是从第5代以后的进一步寻优效果就有些不明显了,此时另外一张对数坐标图就可以派上用场了:
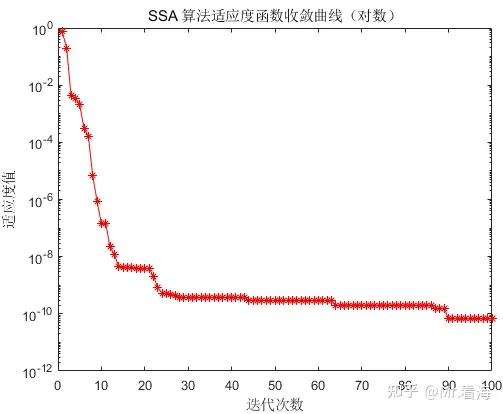
适应度函数收敛曲线-对数坐标
可见从第三代之后,程序还是在不断逼近最优解的。
程序运行完之后,还会在命令行窗口打印出寻优结果、最佳适应度值和程序运行时间,这些都是写论文时必要的参数。

如果我们想换成其他优化算法(比如灰狼优化算法,GWO),只需要将设置改成:
OAmethod ='GWO';% 选择使用的优化算法其他的都不用修改,就可以得到以下结果:
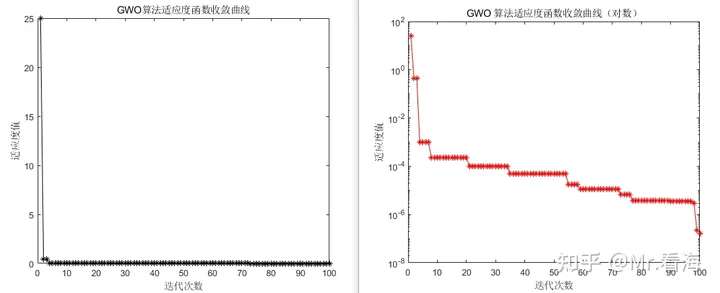
只要你愿意,甚至可以把所有的16种优化算法都试一遍:
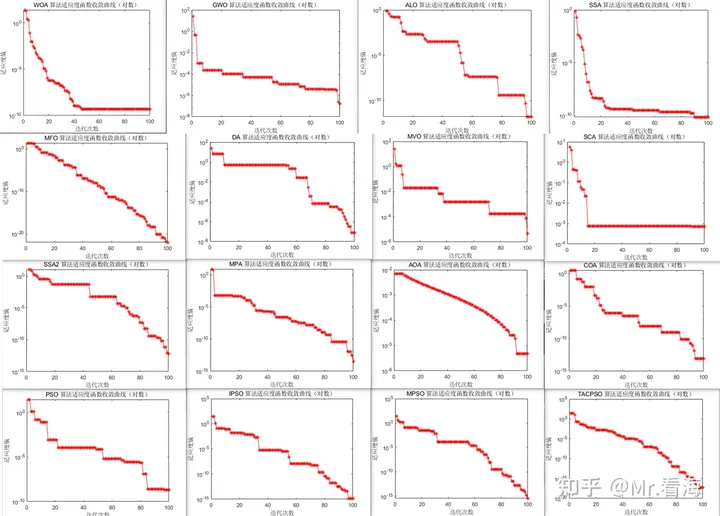
对于上述例子,综合来看MFO飞蛾扑火优化算法的效果是最好的。
上述提到的通用优化算法框架函数的介绍如下:
function [Best_pos,Best_score,curve] = kOptimizationAlgorithm(OAmethod, dataforFitness, lb, ub, dim, pop, Max_iteration)% 通用优化算法框架,该代码提供了多种优化算法的接口。用户可以根据需要选择不同的算法来解决特定的优化问题。% 输入参数:% OAmethod:字符串,指定使用的优化算法。可选方法包括:(截至2024.3.16,共16种方法,后续更新见手册网页:)% 'SSA' - Sparrow Search Algorithm (麻雀搜索算法)% 'GWO' - Grey Wolf Optimizer (灰狼优化算法)% 'WOA' - Whale Optimization Algorithm (鲸鱼优化算法)% 'ALO' - Ant Lion Optimizer (蚁狮优化算法)% 'MFO' - Moth Flame Optimizer (飞蛾扑火优化算法)% 'DA' - Dragonfly Algorithm (蜻蜓优化算法)% 'MVO' - Multi-Verse Optimizer (多元宇宙优化算法)% 'SCA' - Sine Cosine Algorithm (正弦余弦算法)% 'SSA2'- Salp Swarm Algorithm (樽海鞘优化算法)% 'MPA' - Marine Predator Algorithm (海洋捕食者算法)% 'AOA' - Arithmetic Optimization Algorithm (算术优化算法)% 'COA' - Crayfish Optimization Algorithm (小龙虾优化算法)% 'PSO' - Particle Swarm Optimization (粒子群优化算法)% 'IPSO'- 非线性权重粒子群优化算法% 'MPSO'- 运动编码粒子群优化算法% 'TACPSO'- 基于非对称时变加速系数调整策略的粒子群算法% dataforFitness:数据集,用于评估优化问题中目标函数的适应度。% lb:数组,定义了每个参数的下限。% ub:数组,定义了每个参数的上限。% dim:整数,优化问题的维度,即需要优化的参数数量。% pop:整数,优化算法中的种群数量。比如在GWO算法中代表狼群数量% Max_iteration:整数,优化算法的最大迭代次数。%% 输出参数:% Best_pos:数组,表示获得的最佳参数位置。% Best_score:浮点数,最佳位置对应的适应度值。% curve:数组,记录了每次迭代最佳适应度值的变化,用于绘制收敛曲线。
需要上边这个kOptimizationAlgorithm函数文件以及测试代码的同学,可以在公众号 khscience(看海的城堡)中回复“优化算法”获取。
附录
麻雀搜索算法(Sparrow Search Algorithm, SSA): 麻雀搜索算法由Xue和Shen在2020年提出[1]。这种算法模拟了麻雀的觅食行为和反捕食者警戒行为。在SSA中,麻雀分为探索者和追随者两类。探索者在当前最佳位置附近搜索食物,同时使用levy飞行来增强全局搜索能力。追随者则跟随探索者,在局部区域内搜索食物。当探索者发现捕食者时,整群麻雀会迅速飞向安全区域。通过这种机制,SSA可以在全局搜索和局部开发之间取得平衡,高效地解决优化问题。灰狼优化算法(Grey Wolf Optimizer, GWO): 灰狼优化算法由Mirjalili等人在2014年提出[2]。这种算法模拟了灰狼群体的社会等级和狩猎行为。在GWO中,灰狼分为alpha、beta、delta和omega四个等级。alpha狼是群体的领导者,负责做出决策。beta和delta狼协助alpha狼,并参与狩猎。omega狼是服从者,负责跟随其他狼。GWO通过模拟灰狼的围捕、追捕和攻击行为来更新候选解,同时使用一个自适应参数来控制全局搜索和局部开发的平衡。鲸鱼优化算法(Whale Optimization Algorithm, WOA): 鲸鱼优化算法由Mirjalili和Lewis在2016年提出[3]。这种算法模拟了座头鲸的狩猎行为,特别是其独特的气泡网捕食方式。在WOA中,候选解被看作是一群鲸鱼,最优解是捕食的目标。算法通过三种机制来更新鲸鱼的位置:包围猎物、气泡网攻击和搜索猎物。在包围猎物阶段,鲸鱼围绕猎物游动;在气泡网攻击阶段,鲸鱼沿着螺旋路径接近猎物;在搜索猎物阶段,鲸鱼随机搜索猎物。通过这三种机制的交替使用,WOA可以高效地探索和开发搜索空间。蚁狮优化算法(Ant Lion Optimizer, ALO): 蚁狮优化算法由Mirjalili在2015年提出[4]。这种算法模拟了蚁狮的狩猎行为。蚁狮是一种昆虫,其幼虫会在沙地上挖掘漏斗形的陷阱,然后躲在陷阱底部等待猎物。当蚂蚁等昆虫掉入陷阱时,蚁狮会向其抛洒沙粒,使其难以逃脱,最终捕获猎物。在ALO中,候选解被看作是一群蚂蚁,最优解是蚁狮。算法通过模拟蚁狮的建坑、等待、捕食、重建等行为来更新蚂蚁的位置。同时,ALO使用一种适应度平均值的机制来平衡全局搜索和局部开发。飞蛾扑火优化算法(Moth Flame Optimizer, MFO): 飞蛾扑火优化算法由Mirjalili在2015年提出[5]。这种算法模拟了飞蛾在夜间被光源吸引的行为。在算法中,候选解被看作是一群飞蛾,最优解对应光源。飞蛾会围绕光源飞行,但不会直接飞向光源,而是保持一定的距离。算法通过模拟飞蛾的飞行行为来更新解,balance exploration and exploitation,最终找到最优解。蜻蜓优化算法(Dragonfly Algorithm, DA): 蜻蜓优化算法由Mirjalili和Lewis在2016年提出[6]。这种算法模拟了蜻蜓的静态和动态群集行为。在算法中,候选解被看作是一群蜻蜓。蜻蜓的移动由五种因素影响:分离、连贯、吸引、威慑和随机。算法通过模拟这些因素来更新解,在exploration和exploitation之间取得平衡,高效地找到最优解。多元宇宙优化算法(Multi-Verse Optimizer, MVO): 多元宇宙优化算法由Mirjalili等人在2016年提出[8]。这种算法的灵感来自物理学中的多元宇宙理论。在算法中,候选解被看作是一组宇宙,每个宇宙有自己的参数(物理定律)。宇宙之间通过白洞、黑洞和虫洞进行交互。算法通过模拟这些交互来更新解,探索不同的参数空间,最终找到最优解。正弦余弦算法(Sine Cosine Algorithm, SCA): 正弦余弦算法由Mirjalili在2016年提出[9]。这种算法使用正弦和余弦函数来生成候选解。算法开始时,候选解随机分布在搜索空间中。然后,算法通过调整正弦和余弦函数的频率和幅度来更新解,balance exploration and exploitation。这种简单而有效的机制使SCA在许多优化问题上表现出色。樽海鞘群优化算法(Salp Swarm Algorithm, SSA): 樽海鞘群优化算法由Mirjalili等人在2017年提出[10]。这种算法模拟了樽海鞘的链状运动行为。在算法中,候选解被看作是一个樽海鞘链,链头引导整个链的移动。算法通过更新链头的位置来探索新的区域,通过更新追随者的位置来开发已有的解。这种机制使SSA能够在exploration和exploitation之间取得良好的平衡。海洋捕食者算法(Marine Predator Algorithm, MPA): 海洋捕食者算法由Faramarzi等人在2020年提出[11]。这种算法模拟了海洋中捕食者(如虎鲨、虎鲸等)的捕猎行为。在算法中,候选解被看作是一群捕食者。捕食者通过三种阶段来更新自己的位置:高速游动、包围和攻击。这三个阶段分别对应算法的exploration、transition和exploitation。通过模拟捕食者的行为,MPA可以高效地解决许多优化问题。算术优化算法(Arithmetic Optimization Algorithm, AOA): 算术优化算法由Abualigah等人在2021年提出[12]。这种算法的核心思想是使用算术运算(如加、减、乘、除)来更新候选解。算法开始时,候选解随机分布在搜索空间中。然后,算法通过四种算术运算(加法、减法、乘法、除法)来生成新解,同时使用一个自适应的权重来平衡exploration和exploitation。AOA结构简单,易于实现,在许多基准测试问题上表现优异。小龙虾优化算法(Crayfish Optimization Algorithm, COA): 小龙虾优化算法由Zhang等人在2022年提出[13]。这种算法模拟了小龙虾的两种特殊行为:聚集和逃逸。在算法中,候选解被看作是一群小龙虾。当小龙虾遇到食物时,它们会聚集在一起;当遇到威胁时,它们会快速逃逸。算法通过模拟这两种行为来更新解,聚集行为有助于exploitation,逃逸行为有助于exploration,从而高效地找到最优解。粒子群优化算法(Particle Swarm Optimization, PSO): 粒子群优化算法由Kennedy和Eberhart在1995年提出[14]。这种算法模拟了鸟群或鱼群的社会行为。在算法中,候选解被看作是一群粒子。每个粒子有自己的位置和速度,并记住自己找到的最优解。粒子通过跟随群体中的最优粒子来更新自己的位置和速度。通过个体和群体的智慧,PSO可以高效地解决许多优化问题。非线性权重粒子群优化算法(Nonlinear Inertia Weight PSO, IPSO): 非线性权重粒子群优化算法是对标准PSO的一种改进,由Feng等人在2007年提出[15]。这种算法使用非线性的惯性权重来平衡exploration和exploitation。在早期阶段,较大的惯性权重有助于exploration;在后期阶段,较小的惯性权重有助于exploitation。通过动态调整惯性权重,IPSO可以提高算法的收敛速度和解的质量。运动编码粒子群优化算法(Motion-Encoded PSO, MPSO): 运动编码粒子群优化算法由Zhang等人在2019年提出[16]。这种算法使用一种新颖的运动编码方案来表示粒子的位置和速度。在MPSO中,粒子的位置不是直接表示,而是通过一系列运动(如直线运动、旋转运动等)来表示。这种编码方案可以更好地捕捉优化问题的特征,提高算法的性能。非对称时变加速系数粒子群优化算法(PSO with Time-Varying Asymmetric Acceleration Coefficients, TACPSO): 非对称时变加速系数粒子群优化算法由Tian等人在2019年提出[17]。这种算法对标准PSO的加速系数进行了改进。在TACPSO中,个体学习因子和社会学习因子是非对称的,并随时间变化。这种策略可以更好地平衡exploration和exploitation,提高算法的收敛速度和解的质量。参考文献:
[1] Xue, J., & Shen, B. (2020). A novel swarm intelligence optimization approach: sparrow search algorithm. Systems Science & Control Engineering, 8(1), 22-34.
[2] Mirjalili, S., Mirjalili, S. M., & Lewis, A. (2014). Grey wolf optimizer. Advances in engineering software, 69, 46-61.
[3] Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in engineering software, 95, 51-67.
[4] Mirjalili, S. (2015). The ant lion optimizer. Advances in engineering software, 83, 80-98.
[5] Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Systems, 89, 228-249.
[6] Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51-67.
[7] Mirjalili, S., Mirjalili, S. M., & Hatamlou, A. (2016). Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495-513.
[8] Mirjalili, S. (2016). SCA: a sine cosine algorithm for solving optimization problems. Knowledge-Based Systems, 96, 120-133.
[9] Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., & Mirjalili, S. M. (2017). Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163-191.
[10] Faramarzi, A., Heidarinejad, M., Mirjalili, S., & Gandomi, A. H. (2020). Marine predators algorithm: a nature-inspired metaheuristic. Expert Systems with Applications, 152, 113377.
[11] Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., & Gandomi, A. H. (2021). The arithmetic optimization algorithm. Computer Methods in Applied Mechanics and Engineering, 376, 113609.
[12] Zhang, Y., Liu, R., Asghar Heidari, A., Wang, X., Chen, Y., Wang, M., & Chen, H. (2022). Crayfish optimization algorithm: A bio-inspired metaheuristic optimizer for solving constrained engineering problems. Expert Systems with Applications, 195, 116533.
[13] Kennedy, J., & Eberhart, R. (1995, November). Particle swarm optimization. In Proceedings of ICNN'95-international conference on neural networks (Vol. 4, pp. 1942-1948). IEEE.
[14] Feng, Y., Teng, G. F., Wang, A. X., & Yao, Y. M. (2007, August). Chaotic inertia weight in particle swarm optimization. In Second International Conference on Innovative Computing, Informatio and Control (ICICIC 2007) (pp. 475-475). IEEE.
[15] Zhang, J., Xiao, M., Gao, L., & Pan, Q. (2019). Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Applied Mathematical Modelling, 63, 464-490.[16] Tian, D., Zhao, X., & Shi, Y. (2019). Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm and Evolutionary Computation, 51, 100552.