目录
堆算法
概述
向下调整建堆
向上调整建堆
建堆算法
仿函数
概述
使用介绍
emtpy
size
top
push
pop
模拟实现
仿函数
框架
向下调整算法
向上调整算法
pop
push
empty
top
要理解优先级队列,需要有如下知识
STL容器之一的vector,小编写了写了五千字长文详解了vector容器,不过大家只需要知道vector是什么即可http://t.csdnimg.cn/tz9y6
堆算法,虽然小编在学C语言的时候写过一篇,但本篇内容会详细讲解堆算法
仿函数,仿函数属于STL六大组件之一,小编也会精讲
堆算法
概述
小编在学习C语言时写过一篇堆排序,详见http://t.csdnimg.cn/pT5Vw
堆在结构上是一颗二叉树,这颗二叉树只能是满二叉树或完全二叉树。这颗树上的所有数据存放在类似于数组的顺序表中,用顺序表来管理树的数据。(顺序表是一种数据结构,它的底层是线性的空间——存储数据的空间是连续的)
树上的数据是按层序的顺序存入顺序表。如下图
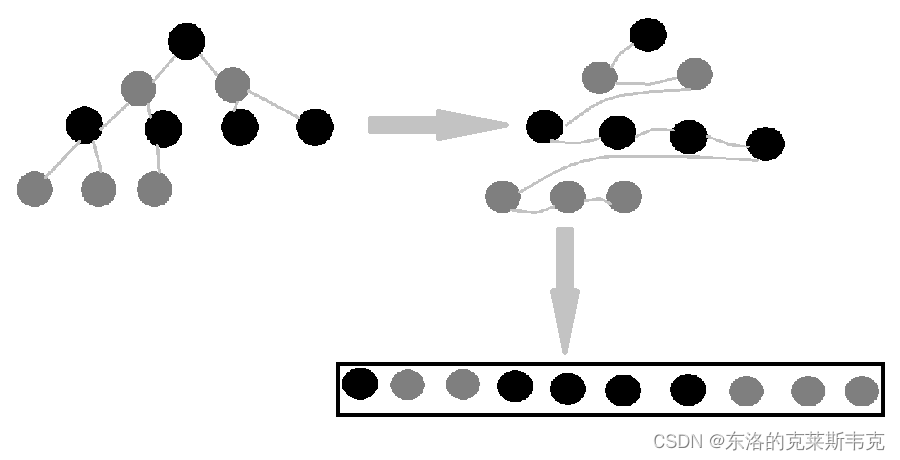
那么顺序表的下标就代表树的节点。父亲节点,左孩子节点,右孩子节点的下标关系如下
| 左孩子节点的下标等于父亲节点的下标乘2加1 |
| 右孩子节点的下标等于左孩子节点的下标加1 |
| 父亲节点的下标等于左孩子节点的下标减1除2 |
| 左孩子节点的下标等于右孩子节点的下标减1 |
到这里大家也看出来了,我们所谓的树结构只是想象的,实际是我们管理的只是类似于数组的顺序表,通过上述公式便可以达到顺序表是一颗树形结构的效果。
为什么非要搞一颗树形结构呢
实际上,只用用树形结构存储数据的话,和顺序表,链表比是没有任何优势的。如果存储数据时加上某些限制,便可以高效的对数据进行排序,查找等。
本来顺序表的排序效率是O(N^2),但如果顺序表管理的是一颗树形结构,那么它的排序效率会被降到O(N * lgN)。O(N * lgN)的效率在所有排序效率中属于第一梯队。
那么在堆存储数据时,存数据时的限制是:父亲节点存入的数据要大于或小于孩子节点存入的数据,如果是大于就是大堆,如果是小于就是小堆。
大堆特性:堆顶的数据是最大的,因为堆顶的节点是所有节点的父亲节点,而存数据时父亲节点存入的数据要大于孩子节点存入的数据,所以堆顶的数据是最大的。
小堆特性:堆顶的树据是最小的,原因同上。
向下调整建堆
如果某一个数据使堆不符合堆的结构,便可以使用向下调整算法。核心逻辑如下
恢复成小堆:
从父亲节点开始
比较出左孩子节点和右孩子节点较小的节点
父亲节点是否大于孩子节点
是:交换父亲节点和孩子节点,并继续比较
否:终止整个逻辑
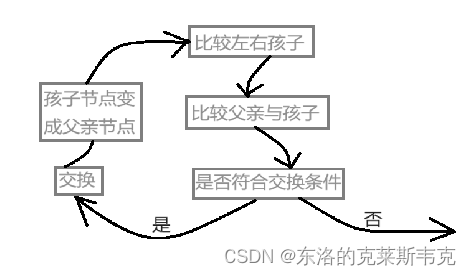

时间复杂度分析:
交换数据最坏的情况下是交换高度次——lgN次。效率是O(lgN)。
向上调整建堆
与向上调整建堆相似,也是一种恢复堆结构的算法。
它是从孩子节点开始,向上比较父亲节点。向上调整建堆是不用比较左右孩子的。每个孩子节点有且只有一个父亲节点。
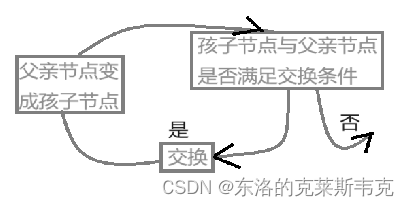
时间复杂度分析:
交换数据最坏的情况下是交换高度次——lgN次。效率是O(lgN)。
建堆算法
如果顺序表中的数据不是一个数据不符合堆结构,而是所有或大部分数据都不符合堆结构呢?
建堆算法就是让顺序表中的无序的数据按照堆结构排序,使顺序表符合堆的结构。
核心逻辑非常简单:
从最后一个父亲节点开始,往前遍历每一个节点,每遍历一个节点就调用一次向下调整算法
最后一个父亲节点的下标等于最后一个孩子节点的下标减1除2
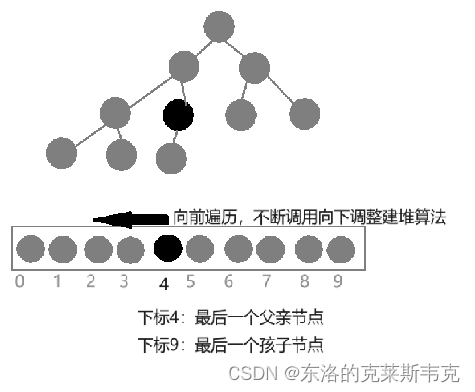
时间复杂度
关于建堆的时间复杂度参考小编的另一篇文章
不推公式,形象理解堆排序的时间复杂度:
http://t.csdnimg.cn/HfH1G
仿函数
仿函数是C++的STL的六大组件之一。
从名字上理解,它具有函数的功能,但不是函数。如果从实现的角度讲的话,叫函数对象比较贴切——有函数功能的对象。
再通俗一点,就是一个类里对 ( ) 进行了运算符重载,不清楚运算符重载的话可参考http://t.csdnimg.cn/1NksT
重载之后,该类实例化的对象即可像函数以样调用,不管从写法还是效果上,与函数无异。如下示意
template <class T> //仿函数 比较是否大于 模板class Less {public:bool operator()(const T& x, const T& y) {return x < y; //如果 x y是自定义类型,那么 < 便是自定义类型的赋值重载(前提是自定义类型支持 < 的赋值重载)}};Less less;//实例化对象
int i = less(3, 5);//像函数一样调用
仿函数的出现是为了代替函数指针。首先函数指针的定义是很繁琐的,可读性极差(虽然可以定义别名)。整个STL的设计都是泛型编程,指针很死板,不适合泛型编程。
概述
到此,所有的知识铺垫完毕,那么什么是优先级队列呢,如下图示意
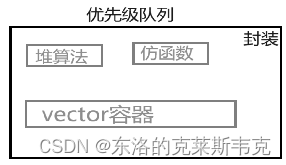
优先级队列实际上还是堆。
vector容器承担顺序表这一数据结构,堆算法负责管理vector容器中的数据,仿函数是为了控制大堆和小堆
优先级队列不提供迭代器,也就是说优先级队列不支持元素遍历。
优先级队列核心功能是入数据和出数据。入数据优先级队列会调用向下调整算法或向上调整算法建堆,出数据会只会出最值
使用介绍
emtpy

| 判断队列是否为空 |
size
| 返回队列数据个数 |
top

| 返回堆顶数据 |
push

| 入数据 |
pop

| 删除数据 |
模拟实现
仿函数
template <class T> //仿函数 比较是否小于class Less {public:bool operator()(const T& x, const T& y) {return x < y; //如果 x y是自定义类型,那么 < 便是自定义类型的赋值重载(前提是自定义类型支持 < 的赋值重载)}};template <class T> //仿函数 比较是否大于class Greater{public:bool operator()(const T& x, const T& y) {return x > y;}};类里的成员函数一定要设计成共有,因为优先级队列要访问。
框架
template <class T, class Container = std::vector<T>, class Comapre = Less<T>> //三个模板参数,<类型, 容器, 仿函数> class priorit_queue{ //......private:Container con;//容器};向下调整算法
//向下调整建堆void AdjustDown(size_t father){//私有接口,不需要检查坐标的合法性Comapre compare; //实例化对象 ,比较大于还是小于传仿函数即可 size_t child = father * 2 + 1; //左孩子的坐标 while (child < con.size()) {if (child + 1 < con.size() && compare(con[child], con[child + 1])) {child += 1;}if (compare(con[father], con[child])){std::swap(con[father], con[child]); //交换两个节点 father = child; //更改下标child = father * 2 + 1;}else{break; //终止循环}}};向上调整算法
void AdjustUp(size_t child){Comapre compare; //实例化对象 size_t father = (child - 1) / 2;while (child > 0) {if (compare(con[father], con[child])){std::swap(con[father], con[child]);child = father;father = (child - 1) / 2;}else{break;}}}向上调整算法和向下调整算法设计成私有即可
pop
void pop() //删除数据{std::swap(con[0], con[con.size() - 1]); //首尾交换 con.pop_back(); //删除尾部数据AdjustDown(0);//重新建堆};push
void push(const T& x) //插入数据{con.push_back(x); //尾插AdjustUp(con.size() - 1); //向上调整算法};empty
bool empty() const //判断是否为空{return con.size() == 0;}top
const T& top() const //返回堆顶元素{ return con[0];}