一、实验背景
波士顿房价预测是一个经典的机器学习任务,类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同,波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素进行房价预测的模型,如 图1 所示。
对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散的标签,区分为回归任务和分类任务。因为房价是一个连续值,所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题,并用神经网络来实现这个模型。
二、实验内容
2.1 假设空间
影响波士顿房价的因素:
feature_names = [ ‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’,‘AGE’,‘DIS’, ‘RAD’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’, ‘MEDV’ ]
假设多个影响房价的因素和房价之间是线性关系,可用线性方程表示
y i = x 1 w 1 + x 2 w 2 + ⋯ + x n w n + b y_{i}= x_{1}w_ {1}+ x_ {2}w_ {2}+\cdots+x_ {n}w_ {n}+b yi=x1w1+x2w2+⋯+xnwn+b
y = ∑ i = 1 n x i w i + b y= \sum _ {i=1}^ {n}x_ {i} w_ {i} +b y=i=1∑nxiwi+b
2.2 线性回归原理
假设房价和各影响因素之间能够用线性关系来描述:
y = M 2 x j w j + b y= \frac {M}{2}x_ {j} w_ {j} +b y=2Mxjwj+b
模型的求解即是通过数据拟合出每个 w j w_j wj和 b b b。其中, w j w_j wj和 b b b分别表示该线性模型的权重和偏置。一维情况下, w j w_j wj和 b b b 是直线的斜率和截距。
线性回归模型使用均方误差作为损失函数(Loss),用以衡量预测房价和真实房价的差异,公式如下
M S E = 1 n ∑ i = 1 n ( Y ^ i − Y i ) 2 MSE= \frac {1}{n} \sum _ {i=1}^ {n} (\widehat {Y}_ {i}-Y_ {i})^ {2} MSE=n1i=1∑n(Y i−Yi)2
线性回归模型的神经网络结构:
2.3 优化目标
评价指标:使用均方差作为损失函数:衡量预测房价和真实房价的差异
L O S S = 1 n ∑ i = 1 n ( Y ^ i − Y i ) 2 LOSS= \frac {1}{n} \sum _ {i=1}^ {n} (\widehat {Y}_ {i}-Y_ {i})^ {2} LOSS=n1∑i=1n(Y i−Yi)2 考虑所有样本的误差,然后取平均数
Y ^ i \widehat {Y}_ {i} Y i 预测值 ~~~~~~~~~~~~~~~~ Y i Y_ {i} Yi真实值
2.3 优化算法
优化算法:极小化损失函数(反向传播,梯度下降),确定参数 w w w 和 b b b 的值
三、实验过程
3.1 数据处理
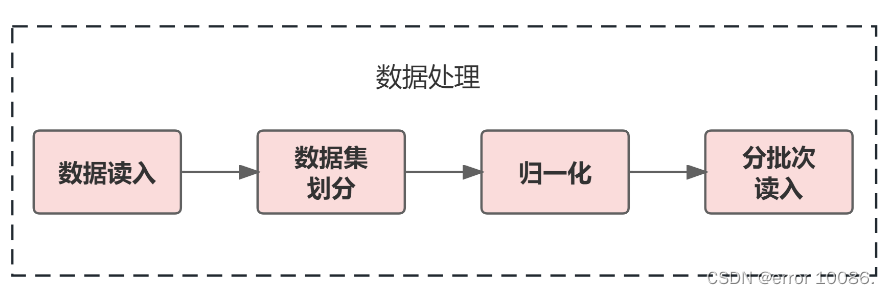
1、数据读入
import numpy as np #导入需要用到的packageimport pandas as pdimport randomdata_path = 'housing.data'feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM','AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]feature_num = len(feature_names)# 数据集列数data = np.fromfile(data_path, sep=' ')data = data.reshape([data.shape[0]//feature_num, feature_num])# 向下取整data#展示数据
2、数据集划分—生成训练集、验证集和测试集
train_num=10eval_num=9train_data = []eval_data = []test_data = []for i in range(len(data)): if i % test_num == 0: test_data.append(data[i]) elif i % eval_num == 0: eval_data.append(data[i]) else: train_data.append(data[i])train_data = np.array(train_data)eval_data = np.array(eval_data)test_data = np.array(test_data)划分比例为:8:1:1
3、数据集处理—归一化
方法一:min-max归一化
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间。
x n e w = x − x min x max − x min x_ {new} = \frac {x-x_ {\min }}{x_ {\max }-x_ {\min }} xnew=xmax−xminx−xmin
其中max为样本数据的最大值,min为样本数据的最小值。这种归一化方法比较适用在数值比较集中的情况。但是,如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定,实际使用中可以用经验常量值来替代max和min。而且当有新数据加入时,可能导致max和min的变化,需要重新定义。
maximums, minimums = train_data.max(axis=0), train_data.min(axis=0) for i in range(feature_num): train_data[:, i] = (train_data[:, i] - minimums[i]) / (maximums[i] -minimums[i]) eval_data[:, i] = (eval_data[:, i] - minimums[i]) / (maximums[i] -minimums[i]) test_data[:, i] = (test_data[:, i] - minimums[i]) / (maximums[i] -minimums[i]) 方法二: z-score归一化
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
x n e w = x − μ σ x_ {new} = \frac {x-\mu }{\sigma } xnew=σx−μ
其中 μ \mu μ是样本数据的均值(mean), σ \sigma σ是样本数据的标准差(std)。此外,标准化后的数据保持异常值中的有用信息,使得算法对异常值不太敏感,这一点归一化就无法保证。
if method == "z-score" : train_data = stats.zscore(train_data, axis=None) eval_data = stats.zscore(eval_data, axis=None) test_data = stats.zscore(test_data, axis=None)最值归一化和均值方差归一化的区别:
最值归一化缩放仅仅跟最大、最小值的差别有关
均值归一化的缩放和每个点都有关系,通过方差体现出来。与归一化
对比,标准化中所有数据点都有贡献(通过均值和标准差造成影响)
归一化后,不同维度之间的特征在数值上有一定比较性,加速模型收敛,可以大大提高分类器的准确性、数据集批次读入
4、数据集分批次读入
mini_batches = [training_data[k:k+batch_size] for k in range(0, n,batch_size) for iter_id, mini_batch in enumerate(mini_batches): x = mini_batch[:, :-1] y = mini_batch[:, -1:]5、数据集乱序分成批次
np.random.shuffle(training_data)3.2 模型设计
构建前向网络结构(假设空间)
def __init__(self, num_of_weights): #为了保持程序每次运行结果的一致性,设置固定的随机数种子 np.random.seed(2023) self.w = np.random.normal(0,0.01,(13, 1)) #使用正态分布随机初始化w self.b = 0 #前向计算 def forward(self, x): return np.dot(x, self.w) + self.b3.3 模型配置
在 Network 类下面添加损失函数
# 计算损失函数 def loss(self, z, y): error = z - y num = error.shape[1] cost = (1/num)*np.sum(np.dot(error,error.T)) return cost3.4 模型训练
循环调用“前向计算+损失函数+计算梯度+反向传播” 更新参数(优化算法)
通过构建的前馈神经网络完成了计算预测值和损失函数
接下来就是如何根据计算出来的损失函数,通过反馈(反向传播和梯度下降)去将神经网络的参数优化到一个最优状态,即机器学习第三个要素—优化算法寻解。
如何去计算和优化参数 w w w 和 b b b 的数值,这个过程也称为模型训练。
模型训练的目标是让定义的损失函数尽可能的小,即根据样本数据,找到一组参数( w w w, b b b)的值,使得 L o s s Loss Loss取最小值。
#反向传播更新权重参数 def update(self, gradient_w, gradient_b, lr): self.w = self.w - lr*gradient_w self.b = self.b - lr*gradient_b def test_or_eval(self,eval_data,batch_size): n= len(eval_data) losses = [] mini_batches = [eval_data[k:k+batch_size] for k in range(0,n,batch_size)] for iter_id, mini_batch in enumerate(mini_batches): x = mini_batch[:, :-1] y = mini_batch[:, -1:] z=self.forward(x) loss = self.loss(z, y ) losses.append(loss) return np.mean(losses) #训练数据集 def train(self, training_data, eval_data, num_epochs, batch_size,lr=0.01): n = len(training_data) losses = [] eval_losses = [] for epoch_id in range(num_epochs): # 在每轮迭代开始之前,将训练数据的顺序随机打乱 # 然后再按每次取 batch_size 条数据的方式取出 np.random.shuffle(training_data) # 将训练数据进行拆分,每个 mini_batch 包含 batch_size 条的数据 mini_batches = [training_data[k:k+batch_size] for k in range(0, n,batch_size)] for iter_id, mini_batch in enumerate(mini_batches): x = mini_batch[:, :-1] y = mini_batch[:, -1:] a = self.forward(x) loss = self.loss(a, y) eval_loss = self.test_or_eval(eval_data,batch_size=batch_size) gradient_w, gradient_b = self.gradient(x, y) self.update(gradient_w, gradient_b, lr) losses.append(loss) eval_losses.append(eval_loss) print("Epoch: %d train_loss= %f,eval_loss= %f"%(epoch_id,loss,eval_loss)) return losses,eval_losses训练结果:
3.5 模型保存和测试
模型的初始训练结果: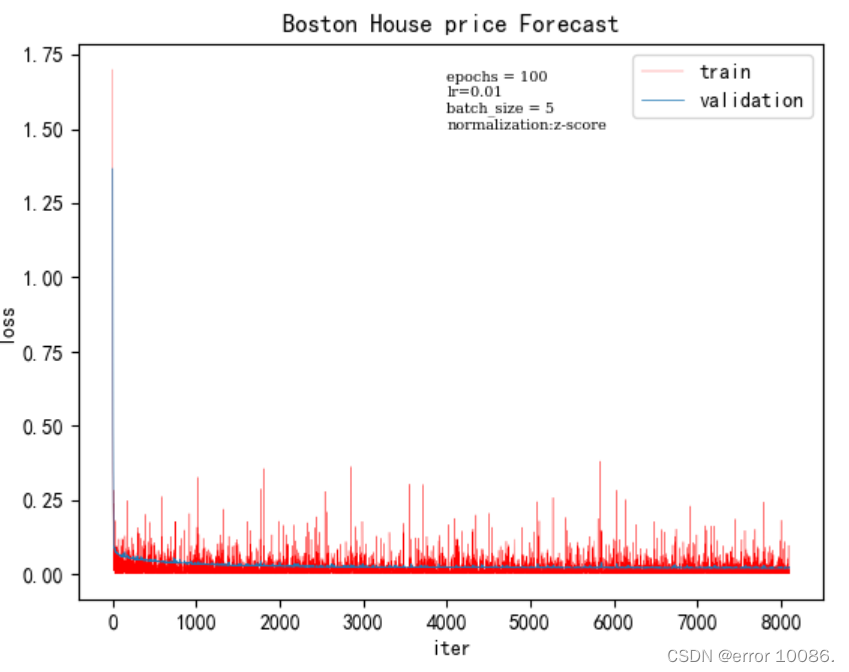
计算测试集的损失:
test_loss = net.test_or_eval(test_data,batch_size=10)test_loss结果为:
![[Pasted image 20231129171042.png]]
四、模型参数调整
1、对epoch的调整
| epoch | 训练时间 | 验证集loss |
|---|---|---|
| 20 | 0.03125 | 0.00186 |
| 50 | 0.078125 | 0.0013 |
| 100 | 0.140625 | 0.0006773 |
| 200 | 0.28125 | 0.000424 |
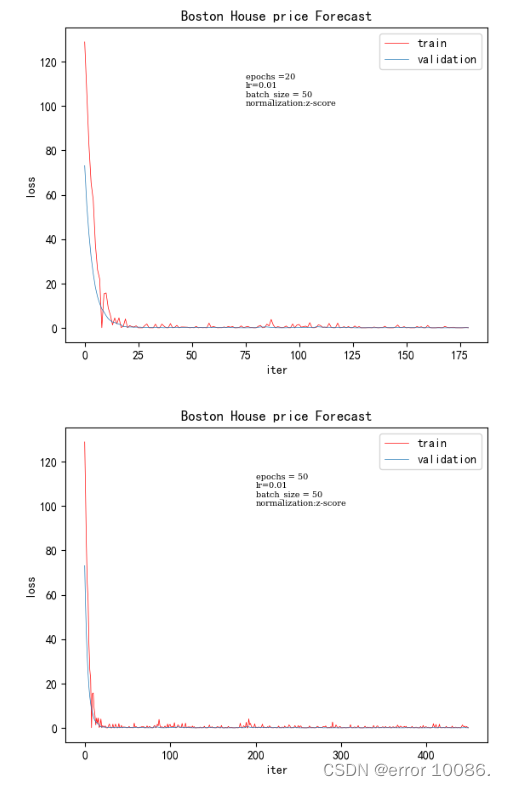

epoch 的数量会影响模型中权重参数的更新,随着 epoch 的增加,模型会逐渐从欠拟合走向过拟合。而我们要的是一个合适的模型,因此就必须选取一个合适的 epoch 更新出来的参数作为我们模型的最终参数(所以在训练模型时可以先将 epoch 设的稍大些,以便选取收敛最合适的时刻,使得模型的拟合效果最优)
根据实验结果可知,随着epoch的增大验证集的loss逐渐减小。
2、对归一化方法的调整
| 归一化方法 | 训练时间 | 验证集loss |
|---|---|---|
| z-score | 0.0625 | 0.0013 |
| max-min | 0.21223 | 0.03698 |
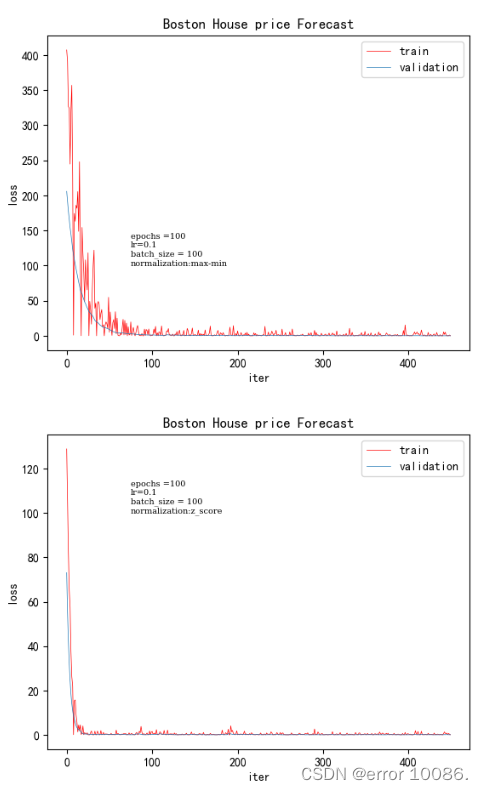
对于归一化方法,本实验采取了两种归一化方法,左图为min_max归一化,右图为z-score归一化,在其他参数不变的情况下,通过改变归一化方法,可以看出,z-score的收敛速度更快,收敛的效果更好,得到的损失值明显减小。
3、对是否打乱数据的调整

在其他超参数不变的情况下,对“是否打乱数据进行”对照,左图未打乱的数据,右图为未打乱训练。可以明显看出,打乱后的数据收敛效果更好,切收敛速度更快,而未打乱的训练损失,呈现明显的规律性,波动性也比打乱后的打,这样训练的结果可能会导致过拟合,模型的泛化能力差。
4、对学习率的调整
| 学习率 | 训练时间 | 验证集loss |
|---|---|---|
| 0.01 | 0.078125 | 0.00130036 |
| 0.05 | 0.0625 | 0.00036027 |
| 0.1 | 0.0625 | 0.0002048 |
| 0.2 | 0.078125 | 未收敛 |
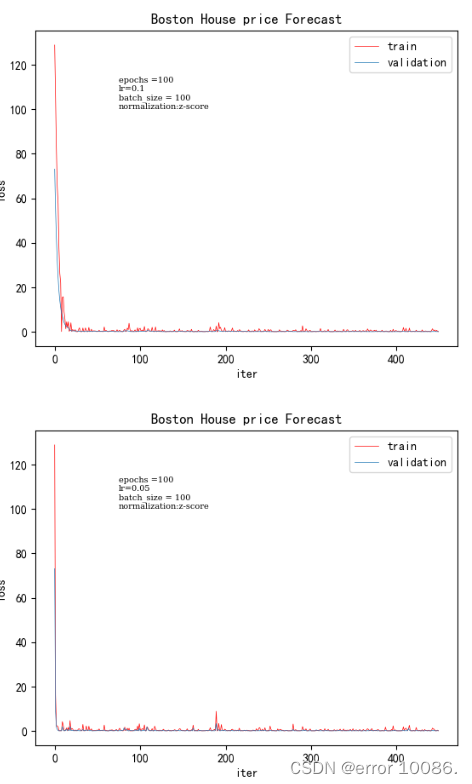
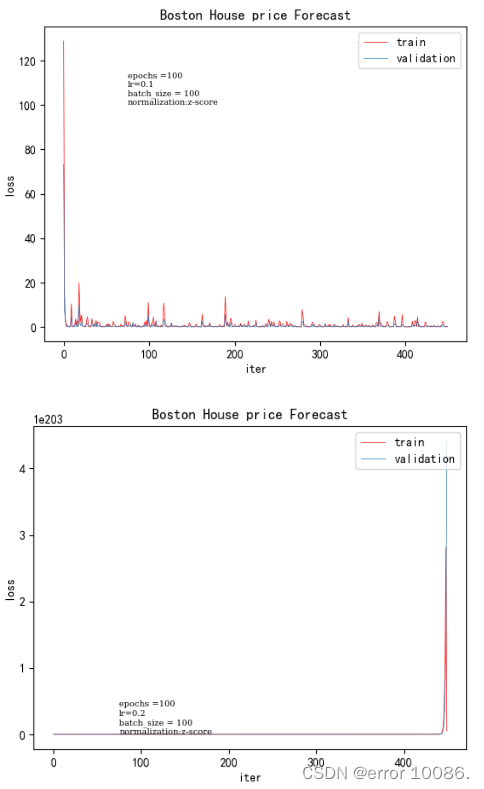
学习率设置太大会造成网络不能收敛,在最优值附近徘徊,也就是说直接跳过最低的地方跳到对称轴另一边,从而忽视了找到最优值的位置
如果学习率设置太小,网络收敛非常缓慢,会增大找到最优值的时间,也就是说从山坡上像蜗牛一样慢慢地爬下去。虽然设置非常小的学习率是可以到达,但是这很可能会进入局部极值点就收敛,没有真正找到的最优解。
可以使用学习率衰减机制
在训练过程中,一般根据训练轮数设置动态变化的学习率。
刚开始训练时:学习率以设置为0.01 ~ 0.001 。
一定轮数过后:逐渐减缓。
接近训练结束:学习速率的衰减应该在100倍以上
指数衰减方式:decayed_lr =lr0*(decay_rate^(global_steps/decay_steps)
参数解释:
decayed_lr:衰减后的学习率,也就是当前训练不使用的真实学习率
lr0: 初始学习率
decay_rate: 衰减率,每次衰减的比例
global_steps:当前训练步数
decay_steps:衰减步数,每隔多少步衰减一次。
5、对batch_size大小的调整
| batch_size | 训练时间 | 验证集loss |
|---|---|---|
| 5 | 0.765625 | 0.02108 |
| 10 | 0.390625 | 0.02504 |
| 50 | 0.078125 | 0.0013003 |
| 100 | 0.046875 | 0.000067729 |
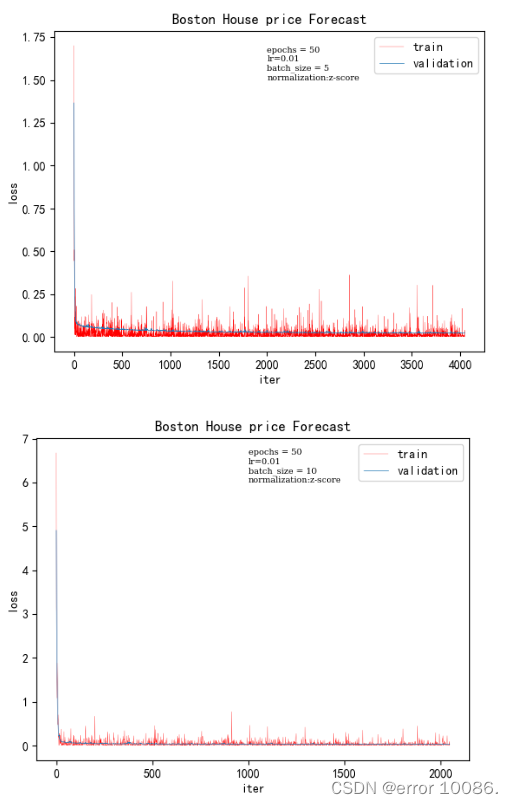

batch_size是一次训练所选取的样本数,它的大小会影响模型的优化程度和速度。理论上来说,batch_size 越大,模型参数的训练速度越快。梯度在计算时用的是一次迭代的数据,即 batch_size 大小的数据,为了使得梯度下降的方向更加精准,就需要合适的 batch_size。
在每个迭代中,模型会处理 Batch Size 个样本并计算其损失,然后使用反向传播算法来更新模型的参数。因此,一个 Epoch 包含了多个迭代,每个迭代包含了 Batch Size 个样本的处理和参数更新。
需要注意的是,在实际训练中,可能需要在数据集的最后一个 Batch 中进行填充,以确保每个 Batch 都有相同数量的样本。填充操作会导致最后一个 Batch 的样本数不足 Batch Size,因此在计算迭代次数时,需要将其考虑在内。
五、实验收获
1 标准化方法选择
对于z-score:数据像正太分布时,使用zscore效果最好,收敛速度更快,z-score会改变原有数据的分布结构,不适合用于对稀疏数据
对于min-max:在本实验中的收敛速度和效果不如z-score,最值归一化缩放仅仅跟最大、最小值的差别有关,将样本数据集映射到[0,1]区间里
2 打乱mini-batch
模型和人有相似的地方,就是对最后看到的样本有更深的印象。即越接近最后的几个批次数据对模型参数的影响越大,通过打乱数据,使用随机抽取的方式,预防训练过拟合,得到更低的损失值。
3 batch_size的选择
batch_size 越大,模型参数的训练速度越快,loss的收敛效果更强。
4 学习率的选择
学习率的过大和过小都会对模型产生影响,因此要不断尝试,找到最优的学习率
通过此次学习,让我进一步了解了深度学习内部的网络结构和工作原理,使得我对模型的认知更加清晰,了解了网络内部的算法,我可以根据自己的想法对模型参数进行调整,得到最优的结果,此次学习也加强了我对深度学习的热爱。