张士玉小黑屋

文章目录一、前言二、命名冲突三、命名空间1、域作用限定符2、命名空间的概念?示例1?示例23、命名空间的定义4、命名空间的使用①指定命名空间访问【做项目】②使用using部分展开【做项目】③使用usingnamespace全局展开【日常练习】5、小结解答：为何使用usingnamespacestd?一、前言相信大部分在学校学习过C++的同学你们的老师一定会和你们说：现在要写C++的代码了，要换一下头文件用#include<iostream>，后面还要带上一个usingnamespacestd;对于前一个头文件的包含和C语言中一样，若是需要使用对应库函数的话就要包一下这个头文件，但是你真的清楚后者吗？今天我们就来聊聊有关C++中命

提示：前面写了A*、Dijkstra算法文章目录前言一、RRT的原理与步骤二、RRT算法编写的步骤1.算法步骤2.算法的实现三、RRT*算法编写的步骤1.算法的步骤2.算法的实现三、所有程序附录RRT算法RRT*算法前言RRT和RRT*的区别：RRT的中文名为快速随机探索树，它的原理很简单，实际上就是维护一棵路径树：从起点开始，在空间中随机采样，并找到路径树上与采样点最接近且能与它无障碍地连接的点，连接这个点与采样点，将采样点加入路径树，直至终点附近区域被探索到。这种方式无法保证得到的路径是最优的。RRT*在RRT基础上做了改进，主要是进行了重新选择父节点和重布线的操作。试想在RRT中，我们的采样点最终与整棵树上和它最近的点连了起来，但这未必是最好的选择，我们的最

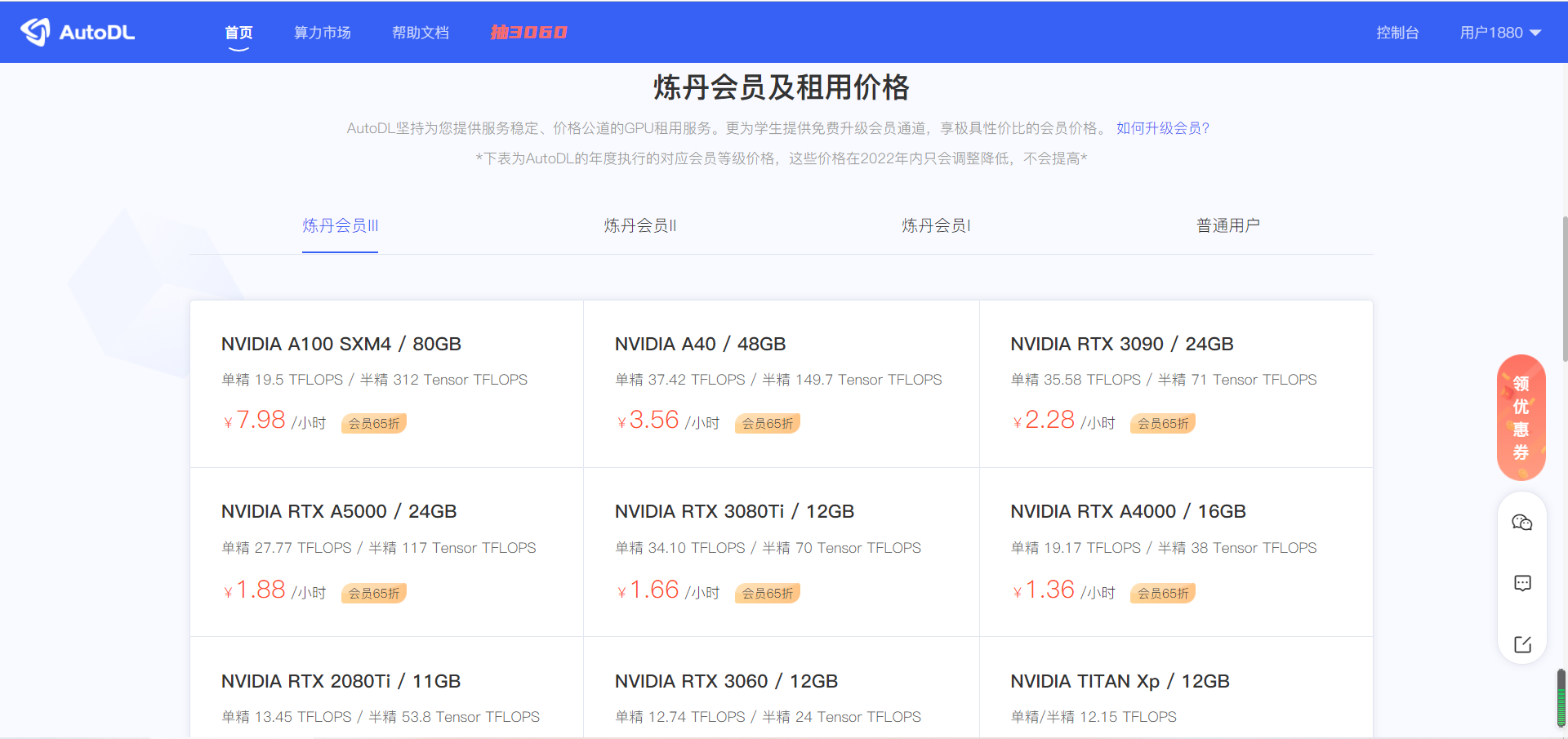
AutoDL是一个国内的GPU租用平台，最近使用了一下，体验感还是很nice的，所以写了篇博客来介绍一下该平台的具体使用方式，也可以当做一个教程来学习^_^网址：AutoDL-品质GPU租用平台-租GPU就上AutoDL一、进入平台页面可以看到下面罗列出了各种GPU的租用价格，还算是比较亲民的。二、创建实例1.注册登录后进入控制台（页面右上角），点击“我的实例”，选择“租用新实例”：2.注册登录后进入控制台（页面右上角），点击“我的实例”，选择“租用新实例”：在页面最下方可以选择镜像，比如我用的是PyTorch1.10+Python3.8+Cuda11.3：点击创建之后我们就能在控制台的“我的实例”中看到已创建的实例：三、使用JupyterLab+Vscode

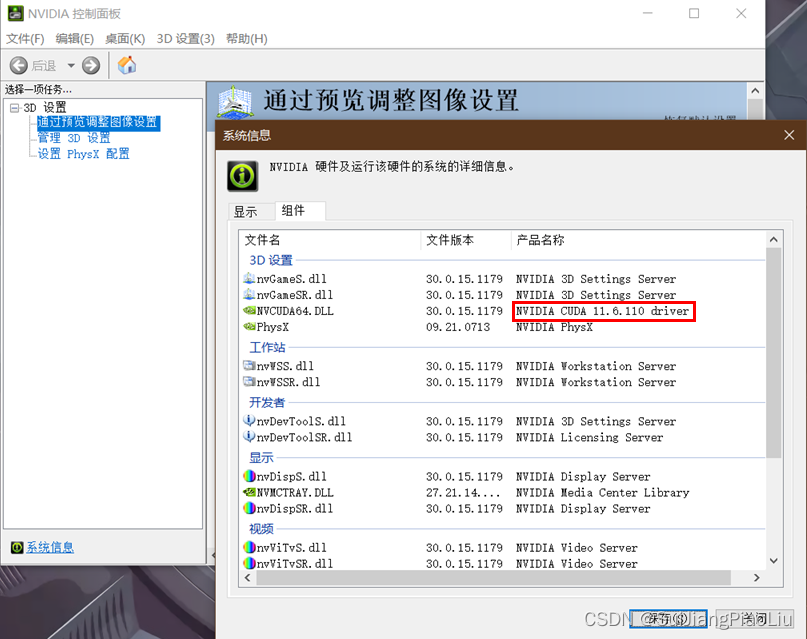
玩转OpenPose【玩转OpenPose】编译篇一、开发环境二、下载与安装2.1CUDA（用于高性能计算）与CUDNN（用于深度神经网络计算的支持）2.2下载Cmake2.3下载0penPose源码2.4下载caffe-openpose源码2.5下载pybind11源码三、编译OpenPose(以上步骤完成-开始编译)3.1编译GPU3.2编译CPU3.3demo测试（GPU版和CPU版都相同）四、建立OpenPoseDemo项目4.1先创建项目，建立bin目录和models目录，bin目录放依赖的相关文件，models放模型文件。4.2将build_GPU(build_CPU)/x64/Release目录下的openpose.dll复制到项目的bin

Python的下载安装1、Python的官网地址：https://www.python.org/2、点击Downloads，然后点击Windows3、选择下载64位安装包【Windowsinstaller(64-bit)】4、打开安装包，这个一定要选上AddPython3.xxtoPATH（不然后续需要自己配置环境变量）5、默认全选，点击Next6、勾选Installforallusers，点击Browse选择安装位置，点击Install7、可选禁用路径长度限制，或者直接点击Close8、到这里安装就结束了，可以检测一下是否成功9、按Windows+R打开运行，输入cmd，点击确定，打开命令提示符10、输入python，

问题描述：我们在开发过程中经常会遇到使用富文本编辑器进行操作，当前插件市场上关于富文本的编辑器挺多的，我们就不一一个介绍了，现在我们主要讲解一些vue-quill-editor富文本编辑器的使用操作和注意事项。效果图具体操作使用1.安装npminstallvue-quill-editor-S2.引入到项目中有两种挂载方式：全局挂载和在组件中挂载，根据自己的项目需求选择，一般用到富文本编辑都是在某一个项目中，我们这里为了方便大家选择，两种引用方案都写下来以便大家参考：（1），页面中引用import{quillEditor}from'vue-quill-editor'import'quill/dist/quill.core.css'import

 文章目录一、动态求连续区间和1、1题目描述1、2 题解关键思路与解答二、数星星2、1题目描述2、2题解关键思路与解答三、数列区间最大值3、1题目描述3、2题解关键思路与解答标题：树状数组与线段树问题作者：@Ggggggtm寄语：与其忙着诉苦，不如低头赶路，奋路前行，终将遇到一番好风景一、动态求连续区间和1、1题目描述题目来源：《信息学奥赛一本通》,Acwing模板题题目难度：简单题目描述：给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。输入格式： 第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。 第二行包含 n 个整数，表

背景开发小伙伴都知道线上服务挂掉，基本都是因为cpu或者内存不足，出现GC频繁OOM之类的情况。本篇文章区别以上的情况给小伙伴们带来不一样的服务挂掉。还记得哔哩哔哩713事故中那场诡计多端的0吗？对就是这个0，和本次事故没关系，但三省同学深受学习。相关阅读：2021.07.13我们是这样崩的线上服务假死解决IDEA插件JProfiler安装使用　Tomcat10下载安装及各个线程作用详解问题排查老规矩在集群环境中同一个服务几个节点无响应。如不及时解决会可能形成雪崩效应。优先查看服务日志是否有报错，礼貌习惯性查看服务cpu及内存情况。先复习下，若服务无报错。cpu或内存出现异常,按如下步骤排查。常规排查1、查看服务进程中线程情况top-H-ppid或

前言本文为【SpringMVC教程】跨域问题相关内容介绍。当一个请求url的协议、域名、端口三者之间任意一个与当前页面url不同时，就会产生跨域。那么究竟什么是跨域，跨域问题该如何解决，本文具体将对同源策略，什么是跨域，简单请求与非简单请求，跨域问题解决等进行详尽介绍~?博主主页：小新要变强的主页?Java全栈学习路线可参考：【Java全栈学习路线】最全的Java学习路线及知识清单，Java自学方向指引，内含最全Java全栈学习技术清单~?算法刷题路线可参考：算法刷题路线总结与相关资料分享，内含最详尽的算法刷题路线指南及相关资料分享~?Java微服务开源项目可参考：企业级Java微服务开源项目（开源框架，用于学习、毕设、公司项目、私活等，减少开发工作，让您只关注业务！）↩

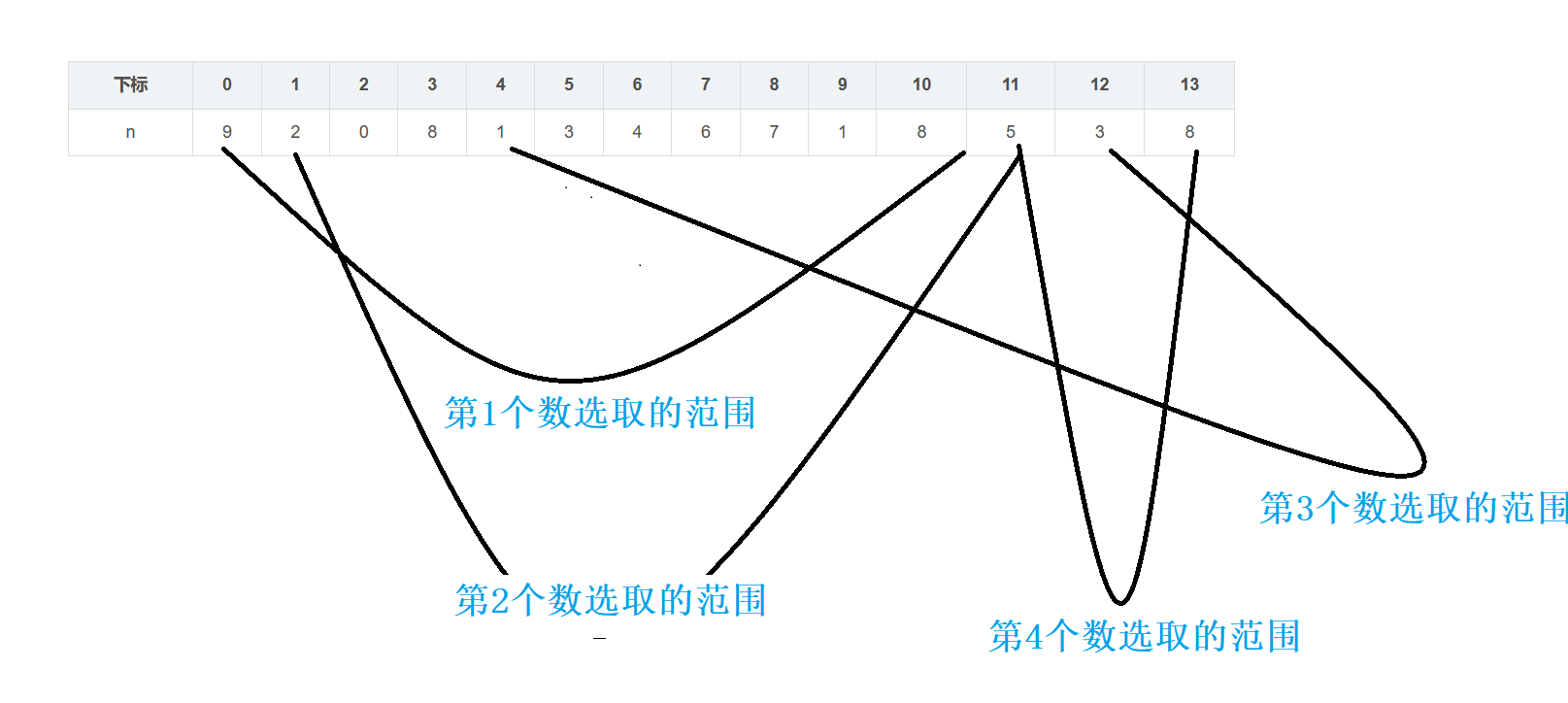
?系列专栏:蓝桥杯?个人主页:个人主页目录1.找零问题①暴力枚举②贪心2.人性总是贪婪的3.堆果子4.图书推荐 1.找零问题有币种1、2、4、5、10若干张，找零n元，输出找零方案。①暴力枚举这是一个找零问题，我们需要找到一种方案，使得用给定的硬币找零时，所需的硬币数量最少。在这个代码中，我们使用了暴力枚举的思路，即枚举每种硬币的数量，然后判断是否能够凑出目标金额。如果能够凑出目标金额，则输出方案。这种方法的时间复杂度为O(n^5)，因为我们需要枚举每种硬币的数量，而硬币的种类有5种，所以总共需要枚举5层循环。这种方法的优点是代码简单易懂，容易实现。缺点是时间复杂度较高，不适用于大规模数据的处理。publicclassA{pu