
文章目录
一、动态求连续区间和
1、1 题目描述
1、2 题解关键思路与解答
二、数星星
2、1 题目描述
2、2 题解关键思路与解答
三、数列区间最大值
3、1 题目描述
3、2 题解关键思路与解答
标题:树状数组与线段树问题
作者:@Ggggggtm
寄语:与其忙着诉苦,不如低头赶路,奋路前行,终将遇到一番好风景

一、动态求连续区间和
1、1 题目描述
题目来源:《信息学奥赛一本通》,Acwing模板题
题目难度:简单
题目描述:给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式:
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 1 开始计数。
输出格式:
输出若干行数字,表示 k=0时,对应的子数列 [a,b] 的连续和。
数据范围:
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 51 2 3 4 5 6 7 8 9 101 1 50 1 30 4 81 7 50 4 8输出样例:
1130351、2 题解关键思路与解答
我们知道求一段区间的和用前缀和数组会很方便,时间复杂度也很快。但是当修改数组的数据时,我们又要重新求前缀和数组,这样下来时间复杂的就较高了,为O(n*n)的级别的。这个时候我们就可以用到树状数组来求解。树状数组是一个一维数组,每个位置存储的数据是一段区间的和。以下为书抓鬼呢数组的模板:
 我们只需要记住树状数组有三个比较重要的函数,lowbit(找下一个要操作的数)、add(改变大小)、query(求区间和)。我们看代码:
我们只需要记住树状数组有三个比较重要的函数,lowbit(找下一个要操作的数)、add(改变大小)、query(求区间和)。我们看代码:
#include <cstdio>#include <cstring>#include <iostream>#include <algorithm>using namespace std;const int N = 100010;int n, m;int a[N], tr[N];int lowbit(int x){ return x & -x;}void add(int x, int v){ for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;}int query(int x){ int res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res;}int main(){ scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); for (int i = 1; i <= n; i ++ ) add(i, a[i]); while (m -- ) { int k, x, y; scanf("%d%d%d", &k, &x, &y); if (k == 0) printf("%d\n", query(y) - query(x - 1)); else add(x, y); } return 0;}二、数星星
2、1 题目描述
题目来源:《信息学奥赛一本通》 , Ural 1028
题目难度:中等
题目描述:
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
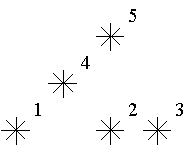
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。
例图中有 1 个 0 级,2 个 1 级 1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
换句话说,给定 N 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式:
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y 表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
输出格式:
N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1 级的星星的数目。
数据范围:
1≤N≤15000,
0≤x,y≤32000。
输入样例:
51 15 17 13 35 5输出样例:
121102、2 题解关键思路与解答
我们仔细分析上述题目,题目中说道:不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。也就是输入的星星的做标顺序是按照从下往上,从左往右依次给出的。我们只需要判断该星星的左下方位置有多少个星星来确定等级就行。由于是按照坐标顺序给出的,所以这就给我们的统计带来了很大的方便。我们只需要看该坐标的横坐标,有多少个比该做的横坐标小的数就是星星的个数。在统计时还不断插入新坐标,相当于就是动态求数组的前缀和,我们在这里就可以利用树状数组即可解决问题。我们看代码:
#include<iostream>#include<cstdio>#include<cstring>#include<algorithm>using namespace std;const int N=32010;int n;int c[N],level[N];int lowbit(int x){ return x&-x;} int sum(int x){ int res=0; for(int i=x;i;i-=lowbit(i)) res+=c[i]; return res;}void add(int x){ for(int i=x;i<N;i+=lowbit(i)) c[i]++;}int main(){ cin>>n; for(int i=0;i<n;i++) { int x,y; scanf("%d%d",&x,&y); x++; level[sum(x)]++; add(x); } for(int i=0;i<n;i++) printf("%d\n",level[i]);}三、数列区间最大值
3、1 题目描述
题目来源:《信息学奥赛一本通》
题目难度:中等
题目描述:输入一串数字,给你 M 个询问,每次询问就给你两个数字 X,Y,要求你说出 X 到 Y 这段区间内的最大数。
输入格式:
第一行两个整数 N,M 表示数字的个数和要询问的次数;
接下来一行为 N 个数;
接下来 M 行,每行都有两个整数 X,Y。
输出格式:
输出共 M 行,每行输出一个数。
数据范围:
1≤N≤1e5,
1≤M≤1e6,
1≤X≤Y≤N,
数列中的数字均不超过2^31−1
输入样例:
10 23 2 4 5 6 8 1 2 9 71 43 8输出样例:
583、2 题解关键思路与解答
我们正常可以想到的就是暴力循环,时间复杂度为O(n*n)的级别。题目中歌的数据范围较大,所以暴力是通过不了的。我们这个时候就可以使用线段树。线段树可以动态求一段区间的和、一段区间的最大值、最小值等问题。这个题中我们就是要求一段区间的最大值。什么是线段树呢?线段树是一棵平衡二叉树。母结点代表整个区间的和,越往下区间越小。注意,线段树的每个节点都对应一条线段(区间),但并不保证所有的线段(区间)都是线段树的节点,这两者应当区分开。
我们在使用线段树时,通常会先建立一个结构体,该结构体包含左右区间,以及要求的值。每个节点 u 的左右子节点的编号分别为 2u 和 2u+1 ,假如节点 u 储存区间 [l,r] 的和,设 mid=⌊(l+r/)2⌋ ,那么两个子节点分别储存 [l, mid] 和 [mid+1,r] 的和。可以发现,左节点对应的区间长度,与右节点相同或者比之恰好多1。
线段树有四个重要的函数:pushup(通过子节点向上求父节点的和)、build(通过递归建立线段树)、query(求一段区间的最大值或最小值或 和)、modify(修该某个值)。
我们来结合本题的代码一起理解一下:
#include<iostream>#include<cstdio>#include<algorithm>#include<cstring>#include<climits>using namespace std;const int N=1e5+10;int w[N];struct Node{ int l,r; int maxv;}tr[4*N];void build(int u,int l,int r){ if(l==r) tr[u]={l,r,w[r]}; else { tr[u]={l,r}; int mid=l+r>>1; build(u<<1,l,mid),build(u<<1 | 1,mid+1,r); tr[u].maxv=max(tr[u<<1].maxv,tr[u<<1 | 1].maxv); }}int query(int u,int l,int r){ if(tr[u].l>=l && tr[u].r<=r) return tr[u].maxv; int mid=tr[u].l+tr[u].r>>1; int maxv=INT_MIN; if(l<=mid) maxv=query(u<<1,l,r); if(r>mid) maxv=max(maxv,query(u<<1|1,l,r)); return maxv;}int main(){ int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&w[i]); build(1,1,n); int l,r; while(m--) { scanf("%d%d",&l,&r); printf("%d\n",query(1,l,r)); } return 0;}