题目pdf下载:第十四届蓝桥杯省赛pdf下载
目录
试题 A: 特殊日期
试题 B: 与或异或
试题 C: 平均
试题 D: 棋盘
试题 E: 互质数的个数
试题 F: 阶乘的和
试题 G: 小蓝的旅行计划
试题 H: 太阳
试题 I: 高塔
试题 J: 反异或 01 串
试题 A: 特殊日期

题意:找出指定时间内,年数是月数和天数的倍数,也就是年%月==0 && 年%日==0
思路:模拟,我的答案是:35813063
就是用for来枚举天数,蓝桥杯挺经常出这个的
代码:
import java.util.*;public class Main { static int pre[]={0,31,28,31,30,31,30,31,31,30,31,30,31}; public static void main(String[] args) { int sum=0; //i是年,j是月,k是日 for(int i=2000;i<=2000000;i++){ for(int j=1;j<=12;j++){ int r=pre[j]; if(j==2 && (i%400==0 || (i%100!=0 && i%4==0))) r++; //2月的闰年是29天 for(int k=1;k<=r;k++){ if(i%j==0 && i%k==0) sum++; if(i==2000000) { //2000000年1月1号过后,直接跳出 i=2000001; j=13; break; } } } } System.out.println(sum); }}
试题 B: 与或异或
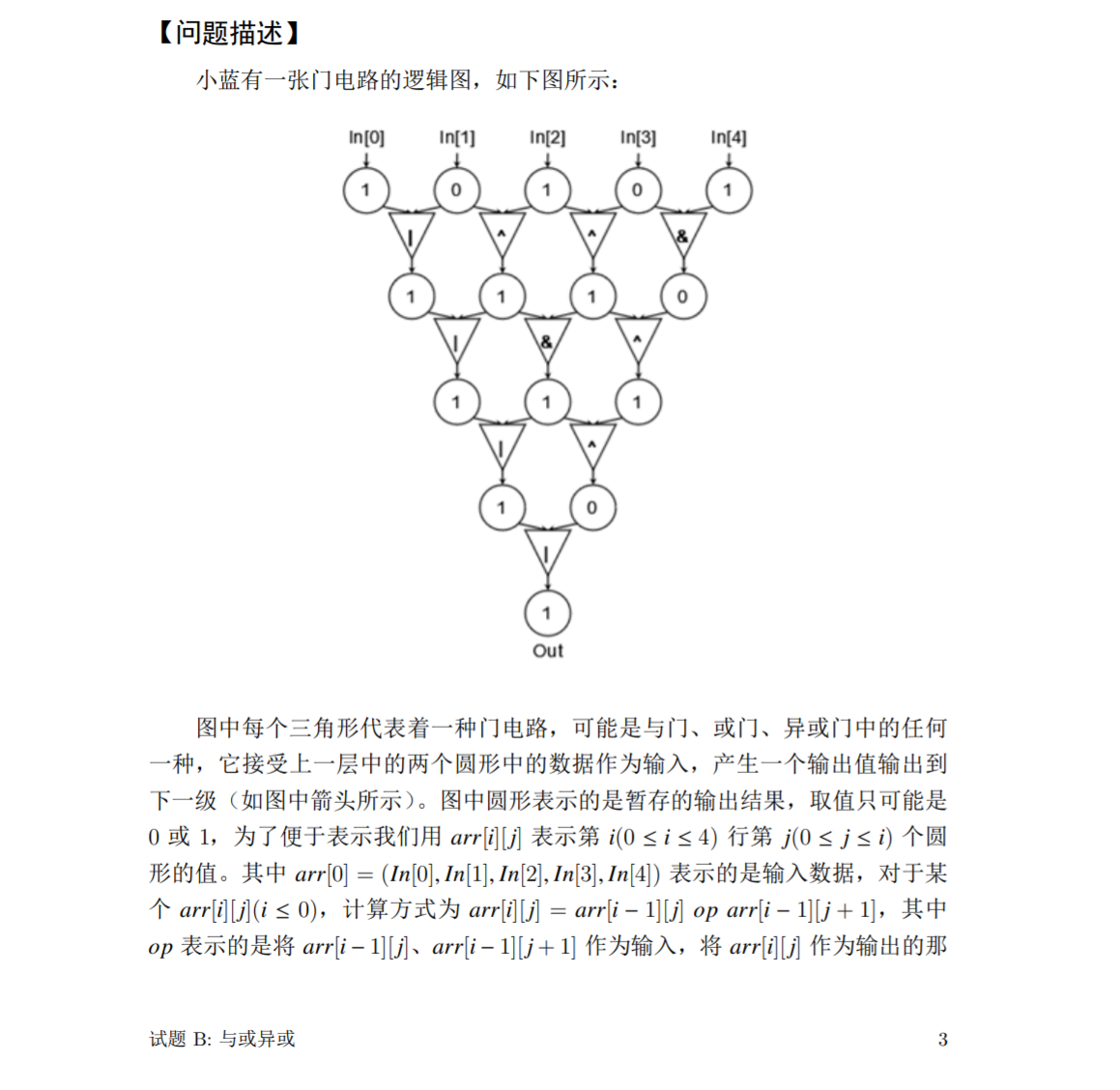
题意:5个数从上往下,相邻的两个两两计算,运算符是&,或|,或^。已知这5个数,求多少种运算符情况可以最后答案是1
思路:dfs搜索,我的答案是:30528
dfs枚举所有运算符的排列情况,就是pow(3,10)=59049种,然后把这5个数从上往下计算,要是最后结果为1答案数+1。
代码(c++写的):
#include <bits/stdc++.h>using namespace std;int sum=0;int a[100005];int dp[10][10];int mp[10][10];void dfs(int d){ if(d==11){ for(int i=1;i<=4;i++) mp[1][i]=a[i]; for(int i=1;i<=3;i++) mp[2][i]=a[i+4]; for(int i=1;i<=2;i++) mp[3][i]=a[i+7]; for(int i=1;i<=1;i++) mp[4][i]=a[10]; for(int i=1;i<=4;i++){ for(int j=1;j<=4-i+1;j++){ if(mp[i][j]==0) dp[i][j]=dp[i-1][j]|dp[i-1][j+1]; if(mp[i][j]==1) dp[i][j]=dp[i-1][j]^dp[i-1][j+1]; if(mp[i][j]==2) dp[i][j]=dp[i-1][j]&dp[i-1][j+1]; } } if(dp[4][1]==1) sum++; return; } a[d]=0; dfs(d+1); a[d]=1; dfs(d+1); a[d]=2; dfs(d+1);}int main(){ dp[0][1]=1; dp[0][2]=0; dp[0][3]=1; dp[0][4]=0; dp[0][5]=1; dfs(1); cout<<sum<<endl; return 0;}
试题 C: 平均

 题意:给若干个数(范围是0-9),和他们的更改的花费,求最小花费,使得0-9最终数量相同
题意:给若干个数(范围是0-9),和他们的更改的花费,求最小花费,使得0-9最终数量相同
思路:贪心
只将数量>n/10的数改为其他数,也就是数量>n/10要改掉 (数量-n/10)个。当然是找其中最小的改
通过:思路的时间复杂度可以100%,具体通过看情况
代码:
import java.util.*;public class Main{public static void main(String[] args){Scanner cin =new Scanner(System.in);int n=cin.nextInt();int A[][]=new int[11][100005];int len[]=new int[15];for(int i=1;i<=n;i++) {int x=cin.nextInt();int y=cin.nextInt();A[x][++len[x]]=y;}for(int i=0;i<10;i++) Arrays.sort(A[i],1,len[i]+1); //排序,不用list是因为没有板子,手敲不出来long sum=0;for(int i=0;i<10;i++) {for(int j=1;j<=len[i]-n/10;j++) {sum+=A[i][j];}}System.out.println(sum);}}
试题 D: 棋盘


题意:一个n*m的棋盘,开始全是白子,选择一个矩形全部反转,最后的棋盘情况打印一下
思路:差分前缀和
就是将这个矩形全部数+1(刚开始全是0),最后%2就是答案
因为最大数据也只是2000,每次在将要改变的行中,差分修改。总执行次数也不过是2000*2000。
最后逐行前缀和,打印这些数%2,注意打印时没有空格
通过:思路的时间复杂度可以100%,具体通过看情况
代码:
import java.util.*;public class Main{public static void main(String[] args){Scanner cin =new Scanner(System.in);int n=cin.nextInt();int m=cin.nextInt();int A[][]=new int[2005][2005];for(int i=1;i<=m;i++) {int x1=cin.nextInt();int y1=cin.nextInt();int x2=cin.nextInt();int y2=cin.nextInt();for(int j=x1;j<=x2;j++) {A[j][y1]++; //差分A[j][y2+1]--;}}for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) {A[i][j]+=A[i][j-1]; //前缀和System.out.print(A[i][j]%2);}System.out.println();}}}
试题 E: 互质数的个数

题意:1-pow(a,b)中有多少个数,和pow(a,b)互质
思路:思维+gcd+快速幂
答案就是pow(a,b-1)*r,r是1-a中和a互质的数量
和a*a*a*a....互质,就是和a互质的数。
a,b互质就是gcd(a,b)==1。而(a,b)和(a,b+a),和(a,b+a*2)...的互质情况是一样的,求gcd()那个公式应该能看出来
也就是有循环,只看1-a就行。而r就是欧拉函数
通过:
欧拉函数求可以100%
100%代码:
import java.util.*;public class Main{ static long mod=998244353; static long Euler(long n){ //求欧拉函数值 long res=n; for(long i=2;i*i<=n;++i){ if(n%i==0){ res=res/i*(i-1); while(n%i==0) n/=i; } } if(n>1) res-=res/n; return res; } static long qpow(long a,long b){ long ans=1; while(b!=0){ if(b%2==1) ans=ans*a%mod; a=a*a%mod; b/=2; } return ans; } public static void main(String[] args){ Scanner cin =new Scanner(System.in); long a=cin.nextLong(); long b=cin.nextLong(); long r=Euler(a); //1-a中有多少个数和a互质 System.out.println(qpow(a,b-1)*(r%mod)%mod); }}
试题 F: 阶乘的和

题意:
思路:这题没有比较好的思路。
只有用乘法求余公式,暴力计算最大的m。
ans=1,2,6,24,120...。计算这些阶乘的和是否是能被ans其整除,也就是判断:
A[1]!%ans+A[2]!%ans+....+A[n]!%ans==0
要是不行的话,就输出当前ans对应的阶乘数。
通过:
可以看到方法不一定能过前40%,但是大多情况下,也有可能过些
代码:
import java.util.*;public class Main{public static void main(String[] args){Scanner cin =new Scanner(System.in);int n=cin.nextInt();int a[]=new int[n+10];for(int i=1;i<=n;i++) {a[i]=cin.nextInt();}long ans=1,p=1;while(true) {long sum=0;for(int i=1;i<=n;i++) {long res=1;for(int j=2;j<=a[i];j++) {res=res*j%ans;}sum=(sum+res)%ans; //算和}if(sum==0) {ans*=(++p);}else {break;}}System.out.println(p-1);}}
试题 G: 小蓝的旅行计划


思路:思维+优先队列
把前面的所有能买的单价和其数量记录下来,然后一旦没有油就从中去除最小的价格。
100%的思路应该是优先队列,存储长度为2的list,每次弹出最小价格,并修改其数量。一旦为0就不再压入。
根据评论,因为油箱有m的上限,所以这个思路不完全正确,具体我也想不到完全正确的思路了
通过:
优先队列,存储长度为2的list可以100%。
代码(优先队列按数量存60%):
import java.util.*;public class Main{ public static void main(String[] args){ Scanner cin =new Scanner(System.in); PriorityQueue q=new PriorityQueue(); int n=cin.nextInt(); int m=cin.nextInt(); long sum=0; for(int i=1;i<=n;i++) { int x=cin.nextInt(); int y=cin.nextInt(); int z=cin.nextInt(); m-=x; while(m<0) { if(q.isEmpty()) { sum=-1; i=n+1; break; } int r=(int)q.poll(); sum+=r; m++; } for(int j=1;j<=z;j++) { q.add(y); } } System.out.println(sum); }}代码(优先队列按序列存100%):
import java.lang.reflect.Array;import java.util.*;public class Main{ static ArrayList fun(int x,int y){ ArrayList<Integer> t=new ArrayList(); t.add(x); t.add(y); return t; } public static void main(String[] args){ Scanner cin =new Scanner(System.in); PriorityQueue<ArrayList<Integer>> q=new PriorityQueue<>(new Comparator<ArrayList<Integer>>(){ @Override public int compare(ArrayList<Integer> a, ArrayList<Integer> b){ return a.get(0)-b.get(0); } }); int n=cin.nextInt(); int m=cin.nextInt(); long sum=0; for(int i=1;i<=n;i++) { int x=cin.nextInt(); int y=cin.nextInt(); int z=cin.nextInt(); m-=x; while(m<0) { if(q.isEmpty()) { sum=-1; i=n+1; break; } List<Integer> r=q.poll(); //前面价格最小的 int res=Math.min(r.get(1),-m); //这次使用r的数量 sum+=(long)res*r.get(0); m+=res; if(res!=r.get(1)) //要是还有剩余,将剩余数量再加入q中 q.add(fun(r.get(0),r.get(1)-res)); } q.add(fun(y,z)); } System.out.println(sum); }}
试题 H: 太阳


题意:给若干个线段,和一个光源。判断有多少个线段可以被光源找到
思路:计算几何
100%的思路没有,只有30%的,也就是双for判断有没有被其他挡到
显示判断可能被挡的,高度至少是被挡<档<光源 or 被挡>档>光源 才有可能会挡到
接下来是被挡线段的两个端点,连接光源后不能与挡的线段相交
方法是叉积求两个线段不相交,要在两点同一侧才不相交
通过:
该思路时间复杂度可以30%,再优的应该是极角排序了
核心代码:
static double add(Node a,Node x,Node y) { //叉积 return (a.x-x.x)*(a.y-y.y)-(a.y-x.y)*(a.x-y.x); } static boolean solve(int i,int j) { //只有高度合适的时候,i才有可能被j挡到 if((b[i]<=b[j] && b[j]<=y) || (y<=b[j] && b[j]<=b[i])) { double h1 = add(new Node(a[j], b[j]), new Node(a[i], b[i]), new Node(x, y)); double h2 = add(new Node(a[j] + l[j], b[j]), new Node(a[i], b[i]), new Node(x, y)); if ((h1 * h2) < 0) return true; h1 = add(new Node(a[j], b[j]), new Node(a[i] + l[i], b[i]), new Node(x, y)); h2 = add(new Node(a[j] + l[j], b[j]), new Node(a[i] + l[i], b[i]), new Node(x, y)); if ((h1 * h2) < 0) return true; } return false; }代码:
import java.util.*;public class Main{ static int n,x,y; static int a[]=new int[1000000],b[]=new int[1000000],l[]=new int[1000000]; static double add(Node a,Node x,Node y) { //叉积 return (a.x-x.x)*(a.y-y.y)-(a.y-x.y)*(a.x-y.x); } static boolean solve(int i,int j) { if((b[i]<=b[j] && b[j]<=y) || (y<=b[j] && b[j]<=b[i])) { double h1 = add(new Node(a[j], b[j]), new Node(a[i], b[i]), new Node(x, y)); double h2 = add(new Node(a[j] + l[j], b[j]), new Node(a[i], b[i]), new Node(x, y)); if ((h1 * h2) < 0) return true; h1 = add(new Node(a[j], b[j]), new Node(a[i] + l[i], b[i]), new Node(x, y)); h2 = add(new Node(a[j] + l[j], b[j]), new Node(a[i] + l[i], b[i]), new Node(x, y)); if ((h1 * h2) < 0) return true; } return false; } public static void main(String[] args){ Scanner cin =new Scanner(System.in); n=cin.nextInt(); x=cin.nextInt(); y=cin.nextInt(); for(int i=1;i<=n;i++) { a[i]=cin.nextInt(); b[i]=cin.nextInt(); l[i]=cin.nextInt(); } int sum=0; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i!=j && solve(i,j)) { break; } if(j==n) sum++; } } System.out.println(sum); }}class Node{ public double x,y; public Node(){} public Node(double a,double b){ this.x=a; this.y=b; }}
试题 I: 高塔


样例算不出来,什么都没有
通过:0%
试题 J: 反异或 01 串

 题意:
题意:
思路:前缀和+回文字串判断
这种题思路感觉细究下就会错
我的思路:反异或操作后,字串只能是以0为中心的奇数长度回文串,或者是偶数长度的任意回文串。只有一次这个操作,且其他都是在两边添加0和1,那么这个回文字串一定还在给的字符串中
所以在其中找回文子串,我用的中心扩展法。用1的数量=左端点的左边1的数量+右端点的右边1的数量+回文字串中的1数量/2
也就是O(n的平方)求出所有情况的最小1的数量
通过:
时间复杂度是O(n的平方),也就是60%。
O(n)或者O(nlogn)求回文子串(不是最长)不知道有没有方法。当然是建立在这个思路正确的前提下
代码:
import java.util.*;public class Main{ static String s; static int f[]=new int[1000000]; static int n,mi=10000000; static int get(int x,int y){ //前缀和 if(y<1 || x>n || x>y) return 0; return f[y]-f[x-1]; } static void solve(int l,int r){ while(l-1!=0 && r+1!=n+1 && s.charAt(l-1)==s.charAt(r+1)){ l--; r++; } mi=Math.min(mi,get(l,r)/2+get(1,l-1)+get(r+1,n)); } public static void main(String[] args){ Scanner cin =new Scanner(System.in); s=cin.next(); n=s.length(); s=" "+s; for(int i=1;i<=n;i++){ f[i]+=f[i-1]+(s.charAt(i)=='1'?1:0); } for(int i=1;i<=n;i++){ if(s.charAt(i)=='0') solve(i,i); if(i!=n && s.charAt(i)==s.charAt(i+1)) solve(i,i+1); } System.out.println(mi); }}