
目录
前言
A.日期统计
B.01串的熵
C.冶炼金属
D.飞机降落
E.接龙数列
F.岛屿个数
G.子串缩写
H.整数删除
I.景区导游
J.砍树
前言
2023年第十四届蓝桥杯C/C++ B组省赛个人题解,欢迎大家提意见!
A.日期统计
题目:
小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的范围之内。
数组中的元素从左至右如下所示:
5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 27 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1 0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3现在他想要从这个数组中寻找一些满足以下条件的子序列:
1. 子序列的长度为 8;
2. 这个子序列可以按照下标顺序组成一个 yyyymmdd 格式的日期,并且
要求这个日期是 2023 年中的某一天的日期,例如 20230902,20231223。
yyyy 表示年份,mm 表示月份,dd 表示天数,当月份或者天数的长度只有一位时需要一个前导零补充。
请你帮小蓝计算下按上述条件一共能找到多少个不同的 2023 年的日期。
对于相同的日期你只需要统计一次即可。
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
输入:
无
输出:
写个程序直接输出结果即可。
问题解析:
蓝桥杯喜闻乐见的关于日期的题目,因为是填空题,没有对复杂度进行限制,所以我们休闲考虑简单枚举,直接进行八重循环即可,但我们仍需注意两个方面:
1、日期的合理性:八重循环的时间消耗实在太大,我们可以在枚举前先进行日期合理性判断,能省去不少无用的循环时间,例如前四位只能是2023,月份的第一位只能是0或1等等。
2、去重:题目明确说明相同日期只统计一次,我们可以使用C++的stl库中的set容器进行去重。
实现代码如下:
#include<cstdio>#include<set>#include<iostream>using namespace std;set<int> st;int a[110];int check[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};int main(){ for(int i=0;i<100;i++) scanf("%d",&a[i]); for(int x1=0;x1<100;x1++){ if(a[x1]!=2) continue; for(int x2=x1+1;x2<100;x2++){ if(a[x2]!=0) continue; for(int x3=x2+1;x3<100;x3++){ if(a[x3]!=2) continue; for(int x4=x3+1;x4<100;x4++){ if(a[x4]!=3) continue; //以上都是判断年份是否为2023 for(int x5=x4+1;x5<100;x5++){ if(a[x5]!=0&&a[x5]!=1) continue; //判断月份的第一位是否为0或1 for(int x6=x5+1;x6<100;x6++){ for(int x7=x6+1;x7<100;x7++){ if(a[x7]!=0&&a[x7]!=1&&a[x7]!=2&&a[x7]!=3) continue; //判断日的第一位是否为0,1,2,3 for(int x8=x7+1;x8<100;x8++){ if(a[x5]*10+a[x6]<=12&&a[x5]*10+a[x6]>=1){ //判断月份是否合理 if(a[x7]*10+a[x8]<=check[a[x5]*10+a[x6]] && a[x7]*10+a[x8]>=1){ st.insert((a[x5]*10+a[x6])*100+a[x7]*10+a[x8]); } } } } } } } } } } printf("%d",st.size()); return 0;}程序运行结果为:235
注意本题是填空题!代码要求直接输出答案,不要输出多于内容,如下:
#include<cstdio>int main(){printf("235");return 0;}B.01串的熵
题目:
对于一个长度为 n 的 01 串 S = x1x2x3...xn.
香农信息熵的定义为:
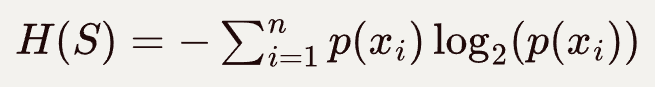
。
其中 p(0), p(1) 表示在这个 01 串中 0 和 1 出现的占比。
比如,对于S = 100 来说,信息熵 H(S ) = - 1/3 log2(1/3) - 2/3 log2(2/3) - 2/3 log2(2/3) = 1.3083。
对于一个长度为23333333 的 01 串,如果其信息熵为 11625907.5798,且 0 出现次数比 1 少,那么这个01 串中 0 出现了多少次?
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
输入:
无
输出:
写个程序直接输出结果即可。
问题解析:
相信大家一眼看到这个题的时候都有点懵,遇到这种题千万不要害怕,慢慢分析理解题目。
首先S是一个01串,n是S的长度,那么对于100串来说,长度为3,其中有1个1,2个0,那么根据题意,p(0)=2/3,p(1)=1/3。
即:H(S ) = - 1/3 log2(1/3) - 2/3 log2(2/3) - 2/3 log2(2/3) = 1.3083。
或:H(S ) = 1*(- 1/3 log2(1/3)) + 2*( - 2/3 log2(2/3) ) = 1.3083
理解了题目给的例子时候,我们来看看需要我们解决的问题:
长度为23333333的01串,给了信息熵H(S)=11625907.5798,要求我们求出01串中有多少个0,即根据H(S)逆推p(0),由于p(0)+p(1)=1,且由题目得知该01串中1的个数更多,我们可以逆推出唯一的p(0),进而根据p(0)和长度n,求出0的个数。
对于代码实现,我们可以对0的个数在1~n/2之间进行遍历,计算H(S)直到H(S)=11625907.5798
代码:
#include<cstdio>#include<cmath>int main(){double eps=0.0001;double HS=11625907.5798;int n=23333333;for(int i=1;i<=n/2;i++){double p0=(double)i/n,p1=1-p0;double ans=(-1.0)*i*p0*log2(p0)+(-1.0)*(n-i)*p1*log2(p1);if(fabs(ans-HS)<eps){printf("%d",i);}}return 0;} 有几点需要注意:
注意数据类型,确保使用浮点数
在判断是否相等时,因为H(S)为保留四位小数,和我们的计算结果有一点差距,无法使用==的方式进行判断是否相等,我们可以取一个可能的最小数,即eps=0.0001,若两个数的差距小于eps,我们就认为这两个数相等。
注意如果需要计算小数的绝对值,需要使用fabs而非abs。
注意本题是填空题!代码要求直接输出答案,不要输出多于内容,如下:
#include<cstdio>int main(){printf("11027421");return 0;}C.冶炼金属
题目:
小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X。
这个炉子有一个称作转换率的属性 V,V 是一个正整数,
这意味着消耗 V 个普通金属 O 恰好可以冶炼出一个特殊金属 X。
当普通金属 O 的数目不足 V 时,无法继续冶炼。
现在给出了 N 条冶炼记录,每条记录中包含两个整数 A 和 B,
这表示本次投入了 A 个普通金属O,最终冶炼出了 B 个特殊金属X。
每条记录都是独立的,这意味着上一次没消耗完的普通金属 O 不会累加到下一次的冶炼当中。
根据这 N 条冶炼记录,请你推测出转换率 V 的最小值和最大值分别可能是多少。
题目保证评测数据不存在无解的情况。
输入:
第一行一个整数 N,表示冶炼记录的数目。
接下来输入 N 行,每行两个整数 A、B,含义如题目所述。
3
75 3
53 2
59 2
输出:
输出两个整数,分别表示 V 可能的最小值和最大值,中间用空格分开。
20 25
评测用例规模与约定:
对于 30% 的评测用例,1 ≤ N ≤ 100。
对于 60% 的评测用例,1 ≤ N ≤ 1000。
对于 100% 的评测用例,1 ≤ N ≤ 10000,1 ≤ B ≤ A ≤ 1,000,000,000。
问题解析:
签到题, 对于每一组数据,我们都可以找到一个区间,在这个区间内的V,都满足:每 V 个普通金属 O 冶炼出一个特殊金属 X,且个数与输入数据A,B相对应。
我们对每一组数据进行判断,可以得到若干个V的区间,将所有区间取交集,得到的区间的左边界即为V可能的最小值,右边界为V可能的最大值。
由于我们只需知道V可能的最大,最小值,所以我们只需判断边界的情况即可,即最后结果的最小值为每个区间左边界的最大值,最大值为每个区间右边界的最小值,这样就可以满足V在所有情况下都合理。
代码:
#include<cstdio>#include<iostream>using namespace std;int main(){int n,minv=-1,maxv=1e9+7; //一定要赋初值,确保能更新最大,最小值 cin>>n;for(int i=0;i<n;i++){int a,b;cin>>a>>b;int l=a/(b+1)+1; //V的区间左边界,即最小值int r=a/b; //右边界minv=max(minv,l);maxv=min(maxv,r);}cout<<minv<<" "<<maxv;return 0;} 对于l,r的求法,如果差一个O就能多冶炼一个X,则此时V是最小的。
如果O整好全部冶炼为X,此时V是最大的。
D.飞机降落
题目:
N 架飞机准备降落到某个只有一条跑道的机场。其中第 i 架飞机在 Ti 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 Di 个单位时间,即它最早
可以于 Ti 时刻开始降落,最晚可以于 Ti + Di 时刻开始降落。降落过程需要 Li个单位时间。
一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落。
请你判断 N 架飞机是否可以全部安全降落。
输入:
输入包含多组数据。
第一行包含一个整数 T,代表测试数据的组数。
对于每组数据,第一行包含一个整数 N。
以下 N 行,每行包含三个整数:Ti,Di 和 Li。
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
输出:
对于每组数据,输出 YES 或者 NO,代表是否可以全部安全降落。
YES
NO
评测用例规模与约定:
对于 30% 的数据,N ≤ 2。
对于 100% 的数据,1 ≤ T ≤ 10,1 ≤ N ≤ 10,0 ≤ Ti , Di , Li ≤ 10^5。
问题解析:
这道题的描述还是比较好理解的,飞机有抵达时刻,盘旋时间和降落所需时间,难点在于我们如何规划飞机的降落顺序,使得所有飞机都能安全降落。
注意看数据范围:N<=10
从这个数据范围基本就锁定了暴搜,使用dfs列出所有情况,如果有满足所有飞机安全降落的方案,就输出YES,如果没有就继续进行搜索,如果将全部的方案搜索完,仍然找不到,就输出NO。
注意这里有个小贪心,如果想让所有飞机安全降落,无疑我们要让飞机尽快降落,题目里也明确提示一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落,若一架飞机结束降落,此时有飞机正在盘旋,我们必须马上着手降落,但如果没有飞机正在盘旋,我们就必须等待下一个飞机到来。如果用代码实现这一思想,本质是对当前时刻和下一架飞机的到达时刻进行比较。
代码(暴搜dfs):
#include<cstdio>#include<iostream>using namespace std;struct plane{int tt,dd,ll;}plane[20]; bool check[20]; //负责标记飞机是否已经降落 bool dfs(int x,int n,int time){if(x>=n) return true; // 说明全部飞机已经安全降落 for(int i=0;i<n;i++){if(!check[i] && plane[i].dd+plane[i].tt>=time){ //如果说这架飞机未降落,且这架飞机可以在上一架飞机降落之后准备降落 check[i]=true; //标记bool res=dfs(x+1,n,max(time,plane[i].tt)+plane[i].ll);//这架飞机降落,继续往后搜索,注意这里让飞机尽早降落。 check[i]=false; //回溯if(res) return true; //找到了一个可行的方案 }}return false; //当前未找到可行方案 }int main(){int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d%d%d",&plane[i].tt,&plane[i].dd,&plane[i].ll);}bool res=dfs(0,n,0);if(res) puts("YES");else puts("NO");}} 这道题目应该也可以用状压DP或贪心的方法解决。
E.接龙数列
题目:
对于一个长度为 K 的整数数列:A1, A2, . . . , AK,我们称之为接龙数列当且仅当 Ai 的首位数字恰好等于 Ai−1 的末位数字 (2 ≤ i ≤ K)。
例如 12, 23, 35, 56, 61, 11 是接龙数列;12, 23, 34, 56 不是接龙数列,因为 56的首位数字不等于 34 的末位数字。所有长度为 1 的整数数列都是接龙数列。
现在给定一个长度为 N 的数列 A1, A2, . . . , AN,请你计算最少从中删除多少个数,可以使剩下的序列是接龙序列?
输入:
第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, . . . , AN。
511 121 22 12 2023
输出:
一个整数代表答案。
1
样例说明:
删除 22,剩余 11, 121, 12, 2023 是接龙数列。
评测用例规模与约定:
对于 20% 的数据,1 ≤ N ≤ 20。
对于 50% 的数据,1 ≤ N ≤ 10000。
对于 100% 的数据,1 ≤ N ≤ 10^5,1 ≤ Ai ≤ 10^9。所有 Ai 保证不包含前导 0。
问题解析:
一道dp题,dp最重要的就是找到数据间的关系,以及状态如何转移。
首先,数据间的关系题目已经明确的告诉了我们,如果这个数字的尾等于下一个数字的头,我们就认为这形成了一个接龙序列。输入数据给了我们一组数列,问我们最少删去几个数,使得这个序列成为一个接龙序列,那换言之,我们只需找到这组数中最长的接龙数列,然后用总长度减去这个接龙数列的长度不就是最少删去数字的个数吗?
下面我们来定义dp[i][j],如过我们想找到最长的接龙数列,我们需要的条件如下:
1.目前我们已经考虑到了n个数字中的第几个数字?
2.在已生成的接龙数列中,最后一位数是什么?因为我们接龙数列是一个数据一个数据链接而成,换言之,我们需要知道目前已经生成的接龙数列的最后一位是什么,以便进行状态转移。
3.目前已经生成的接龙数列的长度是多少?
我们将dp[i][j]定义为,在前i个数中,最后一个数字是j的接龙序列的长度。
其中i是固定的,因为我们必须考虑全部数字,也就是n个数。在状态转移时,我们需要考虑j。
做dp的题目,一定要学会举例子,在有例子的情况下尝试构建状态转移方程。假设这时候来了一个数字,这个数字的首位为L,末位为R。那我们进行状态转移时可以转移到两种状态。
1.不将这个数字加入当前数列,状态转移为:dp[i][R]=dp[i-1][R]。
2.可以将这个数字加入符合条件的数列中,状态转移为:dp[i][R]=dp[i-1][L]+1。
由于我们需要的是最长数列,我们需要将所有状态的最长值保存下来,以便之后的状态转移。
综上,状态转移方程为:dp[i][R]=max(dp[i-1][R],dp[i][R]=dp[i-1][L]+1)
而对于dp[i][j]且j不为R,根据我们的定义,可以得到每个dp[i][j]=dp[i-1][j]。即新来的数字只会影响dp[i][R],以R为尾位的数列需要变化,而尾位是其他数字的数列不受影响。
得到状态转移方程,我们可以开心的解决这道dp题啦!
代码(动态规划):
#include<cstdio>#include<iostream>using namespace std;int dp[100010][10];int main(){int n,ans=-1;cin>>n;for(int i=1;i<=n;i++){string s;cin>>s; //这里使用字符串型,因为字符串型更好找首位 int L=s[0]-'0';int R=s[s.size()-1]-'0';dp[i][R]=max(dp[i-1][R],dp[i-1][L]+1);//状态转移ans=max(ans,dp[i][R]); //数列长度 for(int j=0;j<=9;j++) { //除了dp[i][R]之外,其他的dp[i][j]=dp[i][j-1]if(j==R) continue;else dp[i][j]=dp[i-1][j];}}cout<<n-ans;return 0; }我们可以发现,这个dp[i][j]里的i根本就没有作用啊!相对于dp[i-1],只有dp[i][R]发生了变化,其他的dp[i]=dp[i-1],所以我们可以对dp数组进行简化,代码如下:
#include<cstdio>#include<iostream>using namespace std;int dp[10];int main(){int n,ans=-1;cin>>n;for(int i=1;i<=n;i++){string s;cin>>s; //这里使用字符串型,因为字符串型更好找首位 int L=s[0]-'0';int R=s[s.size()-1]-'0';dp[R]=max(dp[R],dp[L]+1);ans=max(ans,dp[R]); //数列长度 }cout<<n-ans;return 0; }这是一道很适合锻炼dp思维的题,如果是dp比较薄弱的很适合用这道题练手!
F.岛屿个数
题目:
小蓝得到了一副大小为 M × N 的格子地图,可以将其视作一个只包含字符‘0’(代表海水)和 ‘1’(代表陆地)的二维数组,地图之外可以视作全部是海水,每个岛屿由在上/下/左/右四个方向上相邻的 ‘1’ 相连接而形成。
在岛屿 A 所占据的格子中,如果可以从中选出 k 个不同的格子,使得他们的坐标能够组成一个这样的排列:(x0, y0),(x1, y1), . . . ,(xk−1, yk−1),其中(x(i+1)%k , y(i+1)%k) 是由 (xi , yi) 通过上/下/左/右移动一次得来的 (0 ≤ i ≤ k − 1),
此时这 k 个格子就构成了一个 “环”。如果另一个岛屿 B 所占据的格子全部位于这个 “环” 内部,此时我们将岛屿 B 视作是岛屿 A 的子岛屿。若 B 是 A 的子岛屿,C 又是 B 的子岛屿,那 C 也是 A 的子岛屿。
请问这个地图上共有多少个岛屿?在进行统计时不需要统计子岛屿的数目。
输入:
第一行一个整数 T,表示有 T 组测试数据。
接下来输入 T 组数据。对于每组数据,第一行包含两个用空格分隔的整数M、N 表示地图大小;接下来输入 M 行,每行包含 N 个字符,字符只可能是‘0’ 或 ‘1’。
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
输出:
对于每组数据,输出一行,包含一个整数表示答案。
1
3
样例说明:
对于第一组数据,包含两个岛屿,下面用不同的数字进行了区分:
01111
11001
10201
10001
11111
岛屿 2 在岛屿 1 的 “环” 内部,所以岛屿 2 是岛屿 1 的子岛屿,答案为 1。
对于第二组数据,包含三个岛屿,下面用不同的数字进行了区分:
111111
100001
020301
100001
111111
注意岛屿 3 并不是岛屿 1 或者岛屿 2 的子岛屿,因为岛屿 1 和岛屿 2 中均没有“环”。
评测用例规模与约定:
对于 30% 的评测用例,1 ≤ M, N ≤ 10。
对于 100% 的评测用例,1 ≤ T ≤ 10,1 ≤ M, N ≤ 50。
问题解析:
一道很容易看懂的题,很明显是一道连通块的题,我个人在写这种类型的题时喜欢用广搜BFS来写。(如果有对BFS不是很了解的,可以先去做几道类似走迷宫的题目,对理解BFS很有帮助。)
在本题中,1为陆地,0为海水。对于陆地来说,只有上下左右四个方向连通才算连通,而对于海洋来说,只要周围八个格子有海洋就算连通。
我们将该地图存储在(1,1)~(m,n),其他点为0,从(0,0)点开始进行广搜,并将所有搜到的点标为2,广搜结束后,我们发现除了环内的内海,所有海洋都变成了2。
接下来我们直接去搜环的个数,注意现在图中有0,1,2三个数字,2是海洋,我们在代码中可以直接把0和1一视同仁,视为大陆,相当于我们直接把环填充为陆地。
最后统计的结果即为所求。
代码(BFS):
#include<cstdio>#include<iostream>#include<queue>#include<cstring>using namespace std;char g[100][100];int dx[8]={1,-1,0,0,1,1,-1,-1};int dy[8]={0,0,1,-1,1,-1,1,-1};int m,n;struct point{int x,y;}; void bfs_sea(){queue<point> q;g[0][0]='2';struct point startpoint;startpoint.x=0, startpoint.y=0;q.push(startpoint);while(!q.empty()){point temp=q.front();for(int i=0;i<8;i++){ //搜海为8个方向 int xx=temp.x+dx[i];int yy=temp.y+dy[i];if(xx>=0&&yy>=0&&xx<=m+1&&yy<=n+1&&g[xx][yy]=='0'){ //注意这里染色一定要多染一圈,防止边界发生错误 g[xx][yy]='2';q.push({xx,yy}); }}q.pop();} }void bfs_ans(int x,int y){queue<point> q;g[x][y]='2';struct point startpoint;startpoint.x=x, startpoint.y=y;q.push(startpoint);while(!q.empty()){point temp=q.front();for(int i=0;i<4;i++){ //陆地为4个方向 int xx=temp.x+dx[i];int yy=temp.y+dy[i];if(xx>0&&yy>0&&xx<=m&&yy<=n&&(g[xx][yy]=='0'||g[xx][yy]=='1')){g[xx][yy]='2';q.push({xx,yy}); }}q.pop();} }int main(){int t;scanf("%d",&t);while(t--){int count=0;scanf("%d%d",&m,&n);memset(g,'0',sizeof(g));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>g[i][j];}}bfs_sea(); //广搜找到所有外海,并染色for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(g[i][j]=='1'){bfs_ans(i,j);count++;}}}cout<<count<<"\n"; }return 0;}G.子串缩写
题目:
程序猿圈子里正在流行一种很新的简写方法:对于一个字符串,只保留首尾字符,将首尾字符之间的所有字符用这部分的长度代替。例如 internation-alization 简写成 i18n,Kubernetes (注意连字符不是字符串的一部分)简写成 K8s, Lanqiao 简写成 L5o 等。
在本题中,我们规定长度大于等于 K 的字符串都可以采用这种简写方法(长度小于 K 的字符串不配使用这种简写)。
给定一个字符串 S 和两个字符 c1 和 c2,请你计算 S 有多少个以 c1 开头c2 结尾的子串可以采用这种简写?
输入:
第一行包含一个整数 K。
第二行包含一个字符串 S 和两个字符 c1 和 c2。
4
abababdb a b
输出:
一个整数代表答案。
6
样例说明:
符合条件的子串如下所示,中括号内是该子串:
[abab]abdb
[ababab]db
[abababdb]
ab[abab]db
ab[ababdb]
abab[abdb]
评测用例规模与约定:
对于 20% 的数据,2 ≤ K ≤ |S | ≤ 10000。
对于 100% 的数据,2 ≤ K ≤ |S | ≤ 5 × 10^5。S 只包含小写字母。c1 和 c2 都是小写字母。
|S | 代表字符串 S 的长度。
问题解析:
非常简单的一道思维题!
使用后缀和的思想,对c2进行后缀和统计,存储在g数组中,那么其意义为:
对于长度为n的数组g,g[3]=2的概念即为,在原字符串中,3~n之间有2个c2
有了这样一个关于c2的数组g,我们再对字符串进行遍历,对每一个c1进行判断,由于子串最小长度为k,c2的位置最小也要是c1的位置+k-1,换言之,只要是在这个位置后面的c2,都可以与当前的c1组成一个可以被简写的字串,根据我们的后缀和数组,这个数量即为g[c1的位置+k-1]。将所有的c1遍历完,结果相加即为所求。
代码(后缀和):
#include<cstdio>#include<iostream>using namespace std;int g[500010];long long ans;int main(){string s;int k;char c1,c2;cin>>k>>s>>c1>>c2;for(int i=s.size()-1;i>=0;i--){ //后缀和g[i]=g[i+1];if(s[i]==c2) g[i]=g[i+1]+1;}for(int i=0;i+k-1<s.size();i++){if(s[i]==c1) ans+=g[i+k-1];}cout<<ans;return 0;}
H.整数删除
题目:
给定一个长度为 N 的整数数列:A1, A2, . . . , AN。你要重复以下操作 K 次:
每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。输出 K 次操作后的序列。
输入:
第一行包含两个整数 N 和 K。
第二行包含 N 个整数,A1, A2, A3, . . . , AN。
5 3
1 4 2 8 7
输出:
输出 N − K 个整数,中间用一个空格隔开,代表 K 次操作后的序列。
17 7
样例说明:
数列变化如下,中括号里的数是当次操作中被选择的数:
[1] 4 2 8 7
5 [2] 8 7
[7] 10 7
17 7
评测用例规模与约定:
对于 20% 的数据,1 ≤ K < N ≤ 10000。
对于 100% 的数据,1 ≤ K < N ≤ 5 × 10^5,0 ≤ Ai ≤ 10^8。
问题解析:
对于这道题目,我们需要考虑的有两点:
1.如何快速找到一组数里的最小值与最小值的数组下标?
可以使用c++里的优先队列(本质是堆),通过完全二叉树的数据结构特性,让我们以log2N的时间复杂度找到一组数中的最小值,我们可以将权值和结点下标共同作为优先队列的元素,这样我们可以顺利的找到数组下标。
2.如何实现删除一组数中的中某一元素?
如果使用线性存储结构,那删除操作的时间复杂度很大,每次删除都需要对该结点后面的所有结点进行紧缩(即更新位置),对于这道题应该是必然超时,我们可以采用更适合插入,删除操作的链式存储结构,这里我们使用双链表
对于优先队列和双链表,我这里不过多进行讲解,说一下我自己的看法。
优先队列在算法竞赛中使用还是比较频繁的,而且用起来很舒服简单,不了解的同学可以先去学习下如何使用,可以先大致理解为,当插入/删除元素时,他能自动将一组数中最大/最小的数放在队首。学习数据结构时再去研究他的底层逻辑。
双链表,贵在链式存储结构这一思想,链表的思想是必须掌握的,对以后的学习都有很大帮助,而且代码实现也比较简单。
代码(优先队列,双向链表):
#include<cstdio>#include<iostream>#include<queue>using namespace std;long long v[500010],l[500010],r[500010]; //双向链表,注意需要开longlongvoid del(long long x){ //双向链表删除结点。 r[l[x]]=r[x];l[r[x]]=l[x]; //删除结点 v[l[x]]+=v[x];v[r[x]]+=v[x]; //相邻结点加删除结点的权值 }priority_queue<pair<long long,int>,vector<pair<long long,int>>,greater<pair<long long,int>>> q; //优先队列,元素为{权值,结点下标} int main(){int n,k;cin>>n>>k;r[0]=1;for(int i=1;i<=n;i++){cin>>v[i];//记录当前权值l[i]=i-1,r[i]=i+1; //一个记录左边的结点下标,一个记录右边的结点下标。 q.push({v[i],i}); } while(k--){auto temp=q.top(); q.pop(); //取出权值最小的元素if(temp.first!=v[temp.second]) { //注意删除操作会导致一些数据发生变化,必须更新优先队列里的数据。q.push({v[temp.second],temp.second}); k++;continue;}del(temp.second);}for(int i=r[0];i!=n+1;i=r[i]){ //输出 cout<<v[i]<<" "; } return 0;} I.景区导游
题目:
某景区一共有 N 个景点,编号 1 到 N。景点之间共有 N − 1 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行,需要花费一定的时间。
小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 K 个景点:A1, A2, . . . , AK。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 K − 1 个景点。具体来说,如果小明选择跳过 Ai,那么他会按顺序带游客游览 A1, A2, . . . , Ai−1, Ai+1, . . . , AK, (1 ≤ i ≤ K)。
请你对任意一个 Ai,计算如果跳过这个景点,小明需要花费多少时间在景点之间的摆渡车上?
输入:
第一行包含 2 个整数 N 和 K。
以下 N − 1 行,每行包含 3 个整数 u, v 和 t,代表景点 u 和 v 之间有摆渡车线路,花费 t 个单位时间。
最后一行包含 K 个整数 A1, A2, . . . , AK 代表原定游览线路。
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1
输出:
输出 K 个整数,其中第 i 个代表跳过 Ai 之后,花费在摆渡车上的时间。
10 7 13 14样例说明:
原路线是 2 → 6 → 5 → 1。
当跳过 2 时,路线是 6 → 5 → 1,其中 6 → 5 花费时间 3 + 2 + 2 = 7,5 → 1 花费时间 2 + 1 = 3,总时间花费 10。
当跳过 6 时,路线是 2 → 5 → 1,其中 2 → 5 花费时间 1 + 1 + 2 = 4,5 → 1 花费时间 2 + 1 = 3,总时间花费 7。
当跳过 5 时,路线是 2 → 6 → 1,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7,6 → 1 花费时间 3 + 2 + 1 = 6,总时间花费 13。
当跳过 1 时,路线时 2 → 6 → 5,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7,6 → 5 花费时间 3 + 2 + 2 = 7,总时间花费 14。
评测用例规模与约定 :
对于 20% 的数据,2 ≤ K ≤ N ≤ 10^2。
对于 40% 的数据,2 ≤ K ≤ N ≤ 10^4。
对于 100% 的数据,2 ≤ K ≤ N ≤ 10^5,1 ≤ u, v, Ai ≤ N,1 ≤ t ≤ 10^5。保证Ai 两两不同。
问题解析:
首先要明确这实际是个树状结构,最后问的是要花费多少时间,即树上点之间的距离,一眼LCA。
假如树的根结点为 r,那么树上两点 (a,b)之间距离就等于 a 到 r 的距离加上 b 到树根 r 的距离减去两倍 lca(a,b)到树根的距离,这里的 lca(a,b)表示 a 与 b 两点的最近公共祖先,如图所示:
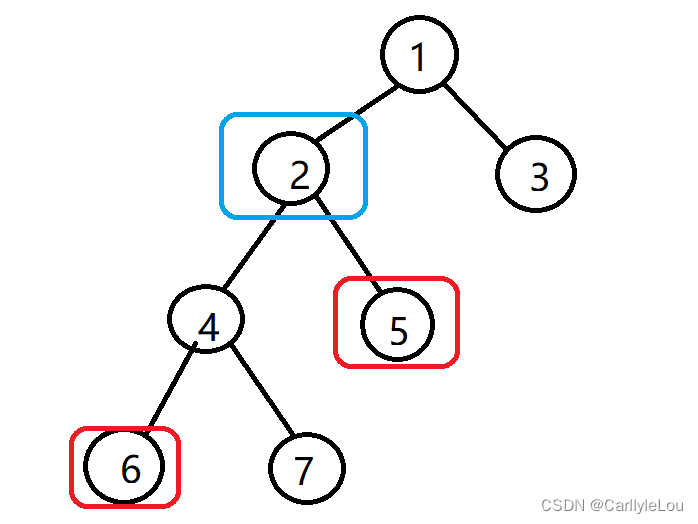
假设我们想知道6结点与5结点之间的距离,我们可以找他们的最近公共祖先,即lca(5,6),在图中该点为2结点。然后我们将5,6结点之间的距离表示为:5到根结点的距离+6到根结点的举例-两倍的2到根结点的举例。即dist[5]+dist[6]-2*dist[2]=2+3-2*1=3。
对于最近公共祖先,有两种常用的算法,分别是Tarjan离线算法和LCA倍增。
下面我简单介绍一下这两种算法,学习LCA,这两种算法都是要求会的,算法竞赛也经常会出题。
Tarjan离线算法是一种基于深度优先搜索(DFS)的算法,它通过遍历整棵树来预处理出每个节点的祖先信息,然后通过查询操作来找到最近公共祖先。
假设在对一棵树进行 DFS 的过程中,对于一对点 a 和 b ,假设会先遍历到a后遍历到b ,很显然 DFS 算法 遍历完 a 后,回溯到其祖先节点c,再递归遍历c的其它子树,当回溯到某个祖先节点 c, 且 b 恰好也是 c 的子树中的节点,那么这个c点是a的众多祖先中,深度是最深的并且同时是a和b的祖先,那么这个c点就是我们要求的最近公共祖先。
LCA倍增算法是一种基于二进制拆分的算法,它通过预处理出每个节点的2^k级祖先信息,然后通过多次向上跳跃来找到最近公共祖先。
在每一个节点上,记录 log(n) 个节点信息,分别对应向上跳……32,16,8,4,2,1 步 所到达的节点。这样我们只需要 log(n) 步就可以走到根节点。如果大的跳不过去就跳小,一定要从大到小开始跳,要实现这个算法需要先找到每个点的深度及他们2^i次的祖先。这个过程一般称为预处理,预处理完成后就可以进行倍增LCA了,先把两个点提到同一高度,再统一开始跳。
但我们在跳的时候不能直接跳到它们的LCA,因为这样可能会跳过最近公共祖先,而是输出公共祖先(而非最近),为了防止误判,要跳到它们LCA的下面一层,然后输出它们的父节点,这样就不会误判了。
求出两点间的lca后,我们可以得到 A1, A2, . . . , AK 线路的总距离sum。
根据题意,我们需要删除其中一个点,除了A1和AK需要特判之外,假如我们删除Ai:
先从sum中减去Ai-1 ~ Ai的距离,再减去Ai ~ Ai+1 的距离,再加上Ai-1 ~ Ai+1 的距离。
代码(倍增LCA) O(nlogn):
#include<cstdio> #include<iostream>#include<vector>using namespace std;vector<pair<int,int>> g[100010]; // 存储图的邻接关系和边权值vector<int> ini; // 存储给定的一系列节点int n,k; // 节点数和给定节点数long long dep[100010]; // 记录节点的深度long long f[100010][22]; // 记录节点的祖先long long dist[100010]; // 记录节点到根节点的距离long long sum; // 完整路径的距离和void dfs(int u,int fa,long long x) { // LCA的预处理 u表示当前结点,fa表示当前结点的祖先 dep[u]=dep[fa]+1; // 更新节点u的深度,深度为父节点fa的深度加1 dist[u]=x; // 记录节点u到根节点的距离 f[u][0]=fa; // 记录节点u的第1个祖先为父节点fa for (int i=1;(1<<i) <= dep[u]; i++) { f[u][i]=f[f[u][i-1]][i-1]; // 使用倍增法,计算节点u的其他祖先,其中f[u][i]表示节点u的第2^i个祖先,即u的2^i祖先等于u的2^(i-1)祖先的2^(i-1)祖先 //即2^i = 2^(i-1) + 2^(i-1) } for (auto &p : g[u]) { // 遍历节点u的邻接边 if (p.first == fa) continue; // 如果邻接边指向的节点是当前节点的父节点,则跳过 dfs(p.first, u, x + p.second); // 递归处理邻接边指向的节点,更新节点的深度和距离 } }int lca(int a,int b){ // 计算节点a和节点b的最近公共祖先 if(dep[a]<dep[b]) swap(a,b); // 确保节点a的深度不小于节点b的深度 for(int i=20;i>=0;i--){ if(dep[f[a][i]]>=dep[b]) a=f[a][i]; // 向上跳跃,将节点a移动到与节点b同一深度的位置 if(a==b) return a; // 如果节点a和节点b相等,则返回它们的值(它们是最近公共祖先) } for(int i=20;i>=0;i--){ if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i]; // 同时向上跳跃,直到找到最近公共祖先的父节点 } return f[a][0]; // 返回最近公共祖先的值}long long get(int a,int b){ // 计算节点a和节点b之间的距离 return dist[a]+dist[b]-2*dist[lca(a,b)]; // 节点a到根节点的距离 + 节点b到根节点的距离 - 2倍的最近公共祖先到根节点的距离}int main(){ scanf("%d%d",&n,&k); // 读取节点数和给定节点数 for(int i=1;i<n;i++){ int u,v,t; scanf("%d%d%d",&u,&v,&t); // 读取边的起点、终点和权值 g[u].push_back({v,t}); // 存储邻接关系和边权值 g[v].push_back({u,t}); } for(int i=0;i<k;i++){ int x; scanf("%d",&x); ini.push_back(x); // 读取给定的一系列节点 } dfs(1,0,0); // 进行LCA的预处理 for(int i=1;i<k;i++) sum+=get(ini[i-1],ini[i]); // 计算完整路径的距离和 for(int i=0;i<k;i++){ long long ans=sum; // 初始化答案为完整路径的距离和 if(i==0){ ans-=get(ini[0],ini[1]); // 减去第一个节点和第二个节点之间的距离 } else if(i==k-1){ ans-=get(ini[k-2],ini[k-1]); // 减去倒数第二个节点和最后一个节点之间的距离 } else{ ans-=get(ini[i-1],ini[i]); // 减去前一个节点和当前节点之间的距离 ans-=get(ini[i],ini[i+1]); // 减去当前节点和下一个节点之间的距离 ans+=get(ini[i-1],ini[i+1]); // 加上前一个节点和下一个节点之间的距离 } printf("%lld ",ans); // 输出答案 } return 0;}倍增LCA的模板,为了方便理解,我在代码中添加了较为详细的注释。
J.砍树
题目:
给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2),
. . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai ≠ bj(1 ≤ i, j ≤ m)。
小明想知道是否能够选择一条树上的边砍断,使得对于每个 (ai , bi) 满足 ai和 bi 不连通,如果可以则输出应该断掉的边的编号(编号按输入顺序从 1 开始),否则输出 -1.
输入:
输入共 n + m 行,第一行为两个正整数 n,m。
后面 n − 1 行,每行两个正整数 xi,yi 表示第 i 条边的两个端点。
后面 m 行,每行两个正整数 ai,bi。
6 2
1 2
2 3
4 3
2 5
6 5
3 6
4 5
输出:
一行一个整数,表示答案,如有多个答案,输出编号最大的一个。
4样例说明:
断开第 2 条边后形成两个连通块:{3, 4},{1, 2, 5, 6},满足 3 和 6 不连通,4 和 5 不连通。
断开第 4 条边后形成两个连通块:{1, 2, 3, 4},{5, 6},同样满足 3 和 6 不连通,4 和 5 不连通。
4 编号更大,因此答案为 4。
评测用例规模与约定:
对于 30% 的数据,保证 1 < n ≤ 1000。
对于 100% 的数据,保证 1 < n ≤ 10^5,1 ≤ m ≤ n/2。
问题解析:
22年是砍竹子,23年来个砍树。
先分析下题目,首先这是一棵树,对于一棵树来说,两结点的简单路径是唯一的。
假设我们需要让(a,b)变得不连通,我们只需要砍掉(a,b)简单路径上的任意一条边即可。
那么满足m个无序对不在连通,可以用一个最笨的方法,遍历所有路径,找出这些路径都经过的一条边并砍掉,换言之,我们可以给所有路径经过的边权值+1,如果有符合条件的边,那这条边最后的权值是m,但这种做法的最坏时间复杂度在O(nm)左右,会超时。
这时就需要引入树上差分这一思想。
差分即前缀和的逆运算,即差分数组diff[i]=a[i]-a[i-1],差分和前缀和一样可以实现优化,只不过算法相反。前缀和优化往往是对前缀和数组作差,而差分优化是对差分数组进行前缀和。
树上差分,顾名思义是在树上进行差分优化,例如在这个题目中我们需要的操作是:对每条路径所有经过的路径权值+1。如果引入差分优化的思想,我们只需要对特定点的权值进行修改,所有权值组成差分数组,最后我们需要求值时,用dfs对树进行遍历,并在回溯的时候对差分数组进行前缀和运算就能得出结果。
下面举一个例子:
(树上差分又分为点差分和边差分,下面我只演示边差分,点差分和边差分原理相同,实现略有不同,可以自行去了解)
假如,我们需要将(5,6)这一条路径上的所有边权值都+1,那我们只需修改5,6结点和lca(5,6),即2结点,通式为:
cnt[u]++; cnt[v]++; cnt[lca(u,v)]-=2;
如下图所示:
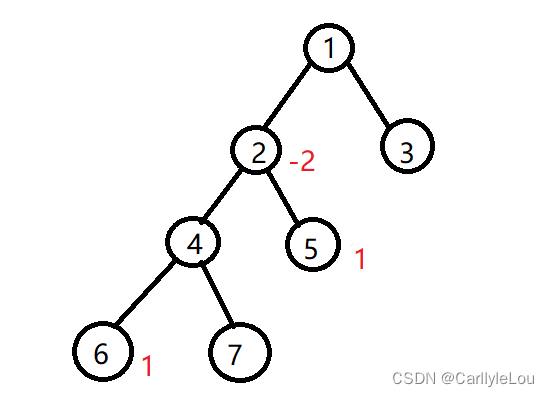
(关于lca公共祖先我已经在上一题I.景区导游中介绍过,这里不再赘述)
关于cnt[u],表示的是u与其父结点相连的边的权值,例如cnt[5],存储的是(2,5)边的权值,是边的权值以子结点数组的方式表示,所以被称为边差分。
那么,为什么可以这样差分呢?
我们不妨模拟一下dfs的过程,需要注意的是,我们是先进行dfs,在回溯的时候进行前缀和。
假设我们已经找到了6结点,并开始回溯,那么我们回溯到2结点时,树的权值如下图所示:

此时按dfs的顺序,会对5结点进行遍历并回溯,同理,得到最终结果如下:
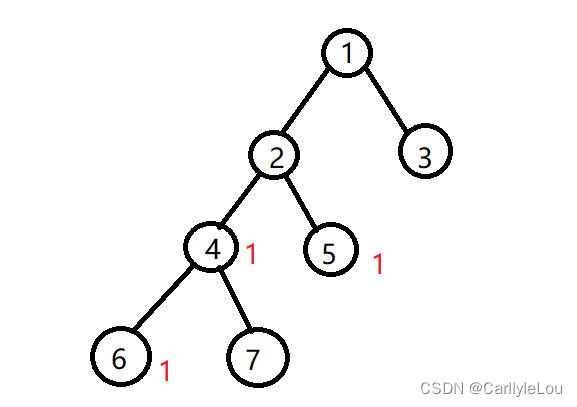
我们可以发现,(5,6)路径上所有的边权值都+1了。
树上差分是基于lca的,它自身的代码很简单,重点在于理解树上差分的思想。
100%做法(树上差分,lca):
#include<cstdio> #include<iostream>#include<vector>using namespace std;vector<pair<int,int>> g[100010]; // 存储图的邻接关系和边权值vector<int> ini; // 存储给定的一系列节点long long dep[100010]; // 记录节点的深度long long f[100010][22]; // 记录节点的祖先long long cnt[100010]; //差分数组long long ID[100010]; //存储编号 int ans=-1; //答案 void init(int u,int fa) { // LCA的预处理 u表示当前结点,fa表示当前结点的祖先 dep[u]=dep[fa]+1; // 更新节点u的深度,深度为父节点fa的深度加1 f[u][0]=fa; // 记录节点u的第1个祖先为父节点fa for (int i=1;(1<<i) <= dep[u]; i++) { f[u][i]=f[f[u][i-1]][i-1]; // 使用倍增法,计算节点u的其他祖先,其中f[u][i]表示节点u的第2^i个祖先,即u的2^i祖先等于u的2^(i-1)祖先的2^(i-1)祖先 //即2^i = 2^(i-1) + 2^(i-1) } for (auto &p : g[u]) { // 遍历节点u的邻接边 if (p.first == fa) continue; // 如果邻接边指向的节点是当前节点的父节点,则跳过 init(p.first,u); // 递归处理邻接边指向的节点,更新节点的深度和距离 ID[p.first]=p.second; //更新边的编号 } }int lca(int a,int b){ // 计算节点a和节点b的最近公共祖先 if(dep[a]<dep[b]) swap(a,b); // 确保节点a的深度不小于节点b的深度 for(int i=20;i>=0;i--){ if(dep[f[a][i]]>=dep[b]) a=f[a][i]; // 向上跳跃,将节点a移动到与节点b同一深度的位置 if(a==b) return a; // 如果节点a和节点b相等,则返回它们的值(它们是最近公共祖先) } for(int i=20;i>=0;i--){ if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i]; // 同时向上跳跃,直到找到最近公共祖先的父节点 } return f[a][0]; // 返回最近公共祖先的值}void add(int a,int b){cnt[a]++;cnt[b]++;cnt[lca(a,b)]-=2; //只修改特定结点。 }void dfs(int u,int fa){ for(auto &x:g[u]){if(x.first!=fa){dfs(x.first,u); //先dfs cnt[u]+=cnt[x.first]; //回溯时再更新路径上的权值 }}}int main(){int n,m; scanf("%d%d",&n,&m); for(int i=1;i<n;i++){ int u,v; scanf("%d%d",&u,&v); // 读取边的起点、终点 g[u].push_back({v,i}); // 存储邻接关系和编号 g[v].push_back({u,i}); } init(1,0); // 进行LCA的预处理 for(int i=0;i<m;i++){ int a,b; cin>>a>>b; add(a,b);}dfs(1,0); //对差分数组 for(int i=1;i<=n;i++){if(cnt[i]==m&&ID[i]>ans) ans=ID[i]; //注意题目里说的,如有多个答案,输出编号最大的一个。 }cout<<ans; return 0;}总结一下,蓝桥杯现在确实上难度了,但弱省依然还是可以暴力省一,虽然23年B组省赛没怎么考dp,dp杯正式更名LCA杯,但我预测24年省赛还是会主考dp,要准备蓝桥杯,基础算法肯定要熟悉,之前很多人觉得省赛不会出LCA和图论,但去年出了,还一下出俩,所以还是要准备的,模板一定要好好背过。背图论,LCA这些模板应付初赛是一定没问题的。
推荐一个讲LCA讲的很好的博文:算法详解之最近公共祖先(LCA) - hulean - 博客园 (cnblogs.com)
最后,祝大家在2024年蓝桥杯中能取得自己满意的成绩!!!
我或许会再写个国赛题解,我是菜狗还没开始补去年国赛题