matlab窗函数-hann窗和hamming窗函数

窗函数的作用

在时域上，窗函数可以看作是对原始信号进行截断或调制的加权函数。这些窗函数通常在时域上是有限的宽度，并且具有对称性，如矩形窗、汉宁窗、汉明窗和布莱克曼窗等。例如，汉明窗是一种对称窗函数，它可以用来平滑信号，减少频谱能量的泄漏，从而提高傅里叶变换后的频率分辨率和精度。

hamming窗

wlen = PRTNumber; %窗函数的长度win = hamming(wlen, 'periodic');%构造hamming窗figure; %绘制汉宁窗plot(win);title('汉宁窗');

图1 hamming窗

hamming汉明窗的特点是两端不能到零。
该matlab函数中有两个参数：

‘symmetric’ - 在使用窗进行滤波器设计时使用此选项；‘periodic’ - 此选项对于频谱分析很有用，因为它使加窗信号可具有离散傅里叶变换中固有的完美周期延拓。当指定 ‘periodic’ 时，该函数计算长度为 L + 1 的窗，并返回前 L 个点；

hann窗

hann窗的matlab函数为hann，使用方法和hamming是相同的，这两种窗有些差异。

wlen = PRTNumber; %窗函数的长度win = hann(wlen, 'periodic');%构造hann窗figure; %绘制hann窗plot(win,'linewidth',1);title('hann窗');

图2 hann窗

hamming窗和hann窗的特点和区别

Hm = hamming(64,'periodic');Hn = hann(64,'periodic');wvt = wvtool(Hm,Hn); %绘制legend(wvt.CurrentAxes,'hamming','hann')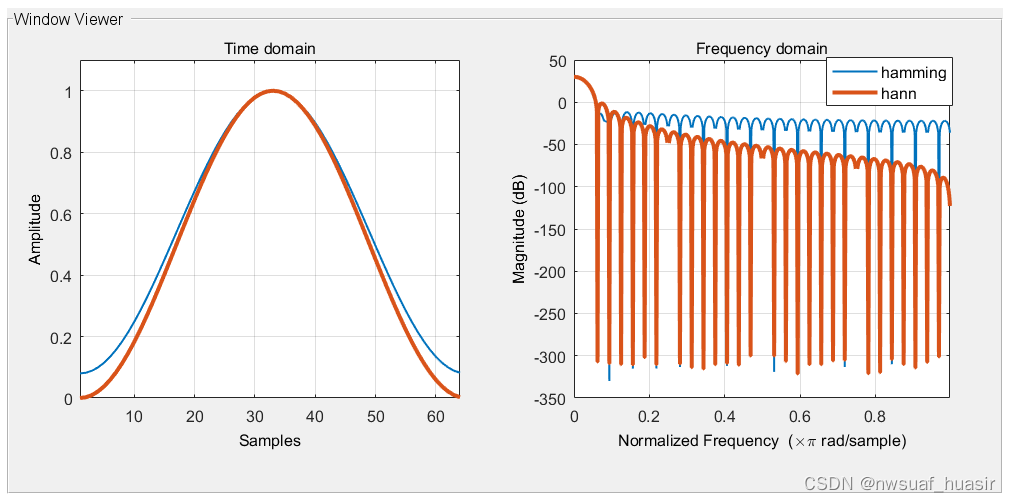

图3 hamming窗和hann窗的区别

汉明窗（hamming）和海宁窗（hann）类似，汉明窗的时域波形两端不能到零，而海宁窗时域信号两端是零。从频域响应来看，汉明窗能够减少很近的旁瓣泄露，但是稍远一点的旁瓣泄露比海宁窗严重。简单点说，hann窗比较稳，短期长期发挥稳定，hamming窗比较激进，短期发挥水平高，长期就没劲了。
Hann的滚降率是大于Hamming的。
那么各种窗函数之间有什么区别呢？结论放在前面。

窗函数有四个评价指标，泄露指数，主瓣宽度，旁瓣衰减，旁瓣滚降率。汉明窗（hamming）和海宁窗（hann）类似，汉明窗两端不能到零，而海宁窗两端是零。汉明窗能够减少很近的旁瓣泄露，但是稍远一点的旁瓣泄露比海宁窗严重。海宁窗（hann）大多数情况下都能满足需求。它同时具有很好的频率分辨率和较少的频谱泄露。如果不知道用什么窗。海宁窗是个不错的选择。

如何选择窗

如果分析对象是单一频率信号的幅度分辨率比频域分辨率更高，则需要宽的主瓣。
如果分析对象是单一频率信号，频域分辨率要求比幅度分辨率更高，则需要更窄的主瓣。