15. 三数之和
题目
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
题目链接
. - 力扣(LeetCode)
画图 和 文字 分析
这道题和 两数之和等于一个值 大体思路是一样的,都是 排序 + 双指针思想
排完序后,我们定义三个指针,一个指向最后一个元素的位置,一个指向首元素的位置,另一个首元素的后一个位置
举例:
输入: [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
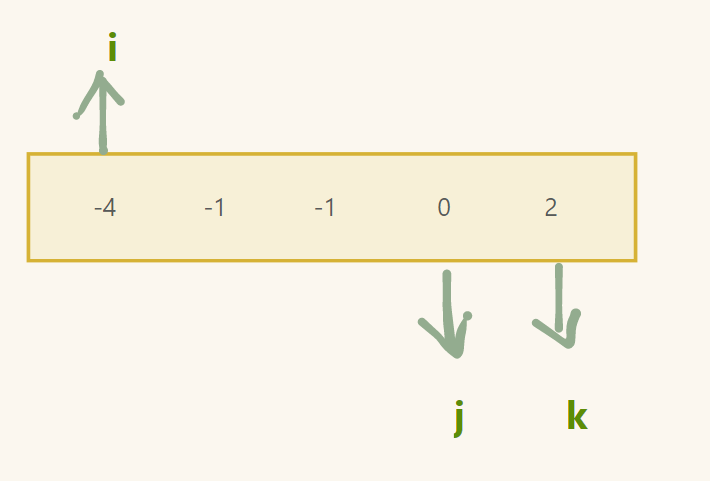
先固定 k不动
如果三者指向的值相加为 0 ,则记录数据 ,再 j++ , k--如果三者指向的值 < 0 ,则 j++如果三者指向的值 > 0 ,则 k--当 i >= j (结束里层循环)
再 i++ , j = i + 1 , k = n - 1
直到 i + 1 >= k (外层循环)
做到以上,只能说完成了完成了不漏掉每一种情况,但现在还有去重的关键一步
去重需要我们在前面的基础上做更改:
第一种情况:
走完上面的步骤 :

判断现在 j 所指的内容 和 j - 1 所指内容是否相同,直到不相同为止(这里需要一个循环,此时要么,j 指向一个不和之前相重复的数,要么越界)
判断 k 同理
上面是里层循环的去重,外层循环也可以去重
当结束里层循环,完成后面的步骤 :
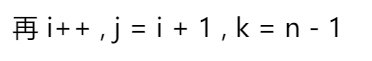
判断 i 所指向的内容 和 i - 1所指向的内容是否相同,直到不相同为止
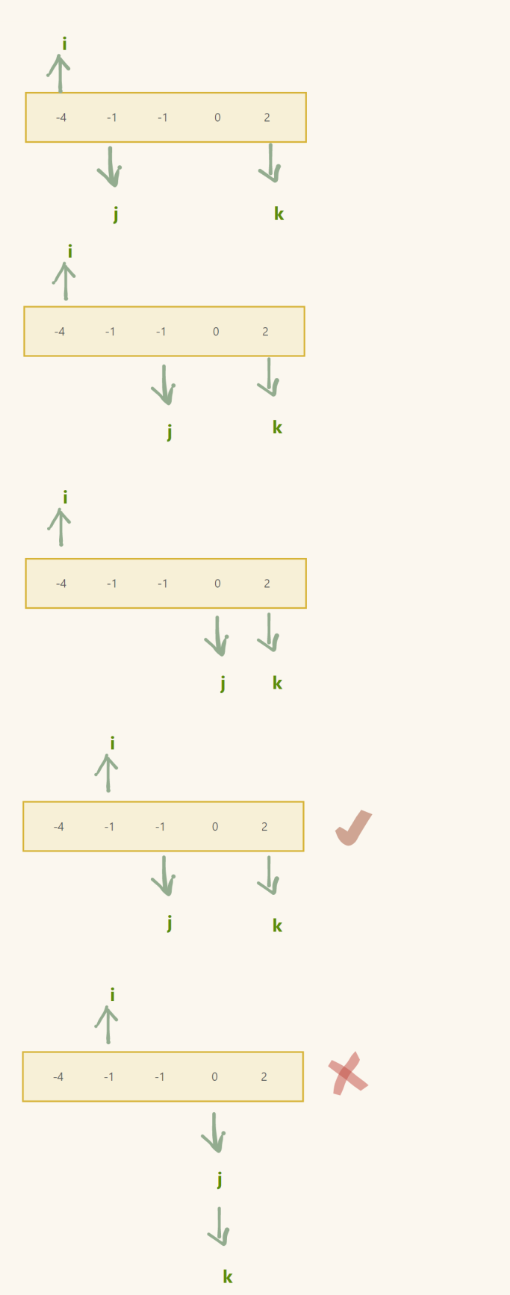

注意:
去重的时候,因为循环的缘故,一定要防止越界
代码
class Solution {public: vector<vector<int>> threeSum(vector<int>& nums) { vector<vector<int>> t; sort(nums.begin(),nums.end()); int i = 0; while(i + 2 <= nums.size() - 1) { int j = i + 1; int k = nums.size() - 1;; while(j < k) { if(nums[i] + nums[j] + nums[k] > 0) { k--; } else if(nums[i] + nums[j] + nums[k] < 0) { j++; } else { vector<int> x; x.push_back(nums[i]); x.push_back(nums[j]); x.push_back(nums[k]); t.push_back(x); int n = nums[j]; int m = nums[k]; k--; j++; while(j < k && n == nums[j]) { j++; } while(j < k && m == nums[k]) { k--; } } } int h = nums[i]; i++; while(i + 2 <= nums.size() - 1 && h == nums[i]) { i++; } } return t; }};
18 . 四数之和
题目
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c 和 d 互不相同nums[a] + nums[b] + nums[c] + nums[d] == target你可以按 任意顺序 返回答案 。
题目链接
. - 力扣(LeetCode)
画图 和 文字 分析
在 leetcode 15. 三数之和 基础之上做出的改变
思想:排序 + 双指针思想
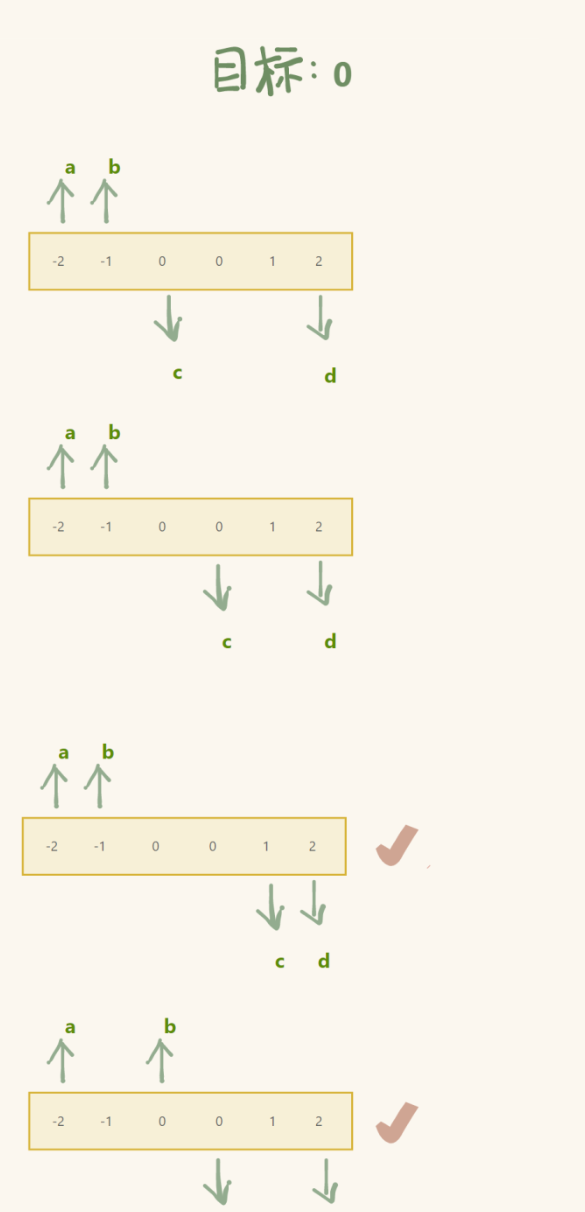
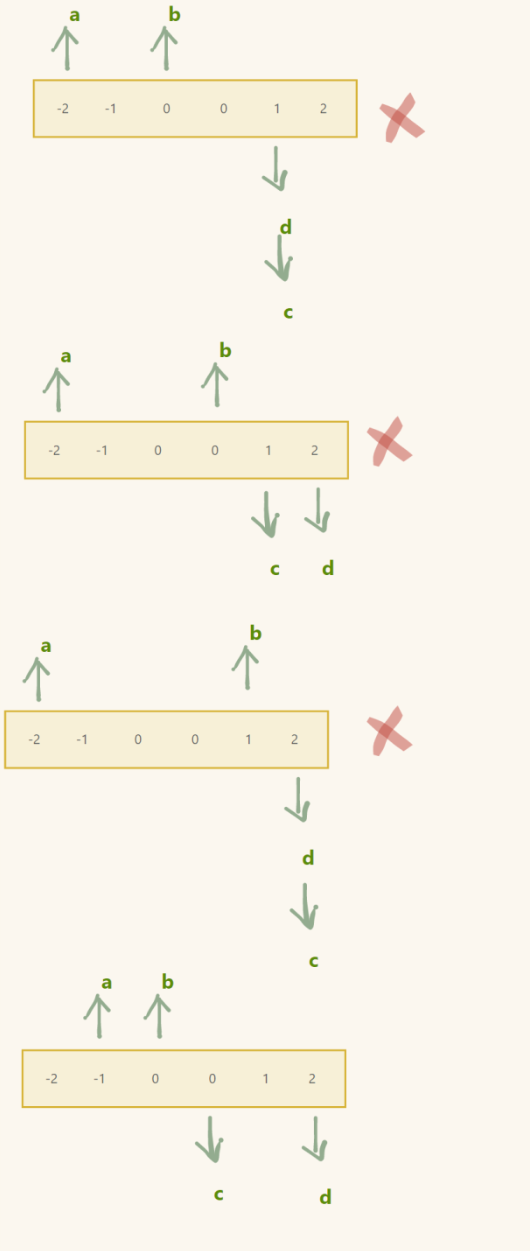
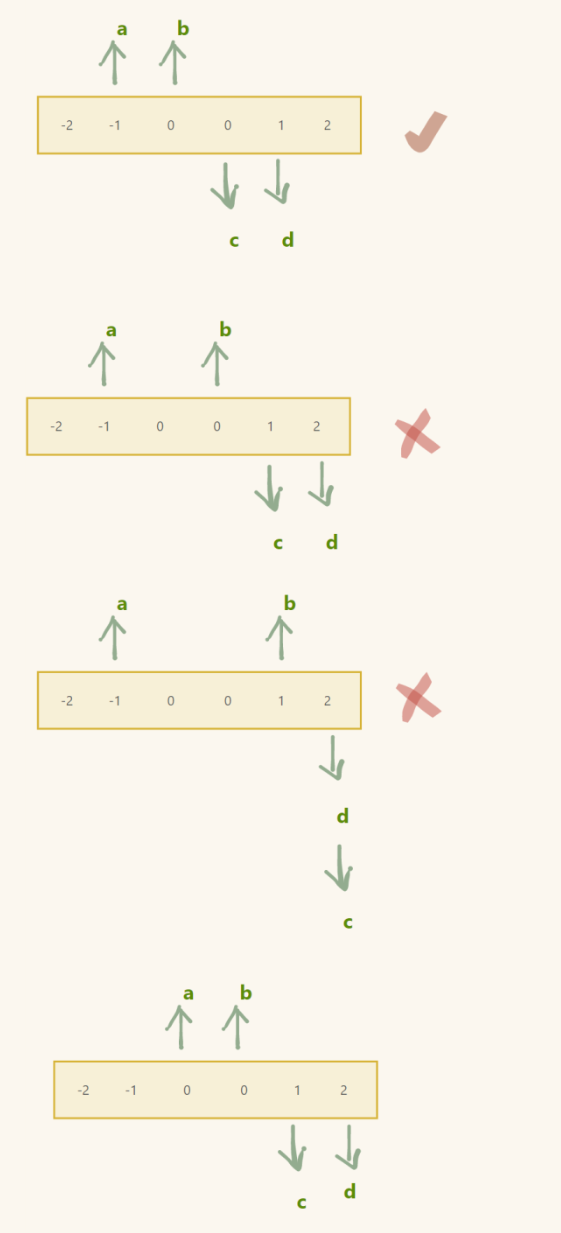
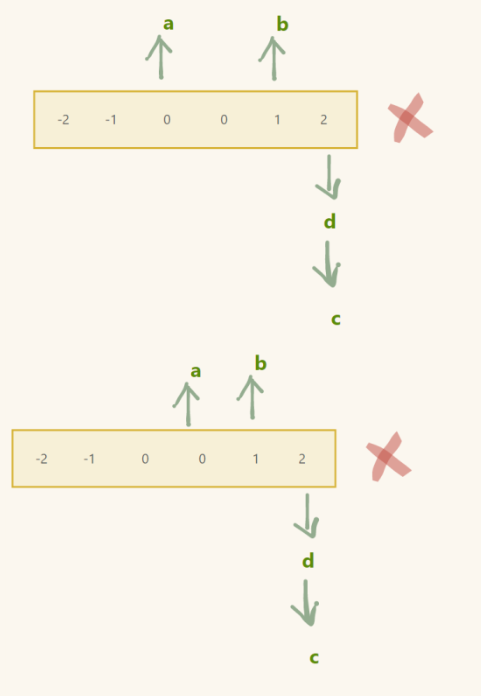
定义四个指针,三个指针分别指向前三个元素的位置,第四个指针指向最后一个元素的位置
举例:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
后面的三个指针和之前的做法一模一样,第一个指针在里层所有循环结束后++
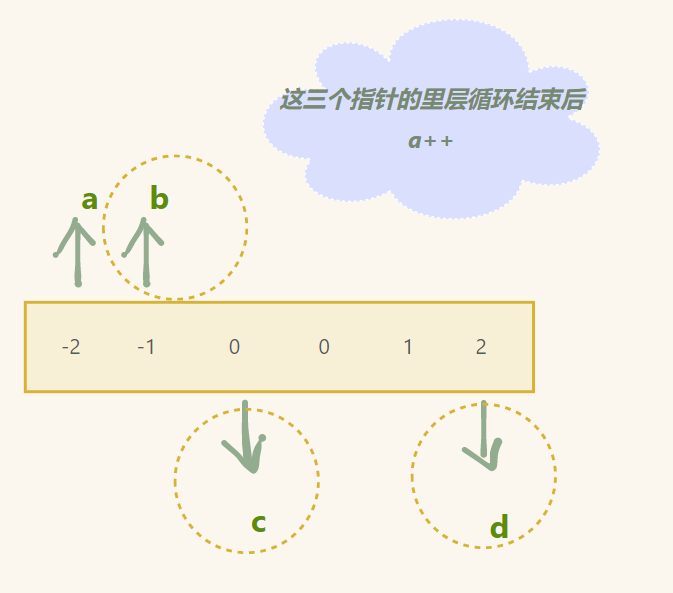
再判断现在 a 所指向的元素和 a - 1 所指向的元素是否相同
直到 a + 2 >= d (外层循环结束)
注意:
注意越界情况判断四数之和是否得到一个值,这里容易由于数据过大发生整型溢出现象,可以改成 longlong 类型 或者针对处理这一可能
代码
class Solution {public: bool iscompare(int &a,int &b,int &c,int &d,int &target) { if(target < 0 && (a >= 0 && b >= 0 && c >= 0 && d >= 0)) { return false; } else if(target > 0 && (a <= 0 && b <= 0 && c <= 0 && d <= 0)) { return false; } else if(target == 0 && ((a > 0 && b > 0 && c > 0 && d > 0) || (a > 0 && b > 0 && c > 0 && d > 0))) { return false; } else { return true; } } vector<vector<int>> fourSum(vector<int>& nums, int target) { vector<vector<int>> s; int n = nums.size() - 1; sort(nums.begin(),nums.end()); int a = 0; while(a + 2 < n) { int b = a + 1; while(b + 1 < n) { int c = b + 1; int d = n; while(c < d) { if(!iscompare(nums[a],nums[b],nums[c],nums[d],target)) { break; } if(nums[a] + nums[b] > target - nums[c] - nums[d] ) { d--; } else if(nums[a] + nums[b] < target - nums[c] - nums[d] ) { c++; } else { vector<int> t; t.push_back(nums[a]); t.push_back(nums[b]); t.push_back(nums[c]); t.push_back(nums[d]); s.push_back(t); int s1 = nums[c]; int s2 = nums[d]; d--; c++; while(c < d && nums[c] == s1) { c++; } while(c < d && nums[d] == s1) { d--; } } } int s3 = nums[b]; b++; while(b + 1 < n && nums[b] == s3) { b++; } } int s4 = nums[a]; a++; while(a + 2 < n && nums[a] == s4) { a++; } } return s; }};
