目录
动态规划的初步理解
求最短路径数
洛谷 P1002 过河卒
题目描述
输入样例
输出样例
思路
AC Code
Everyday English
The greatest glory in living lies not in never falling, but in rising every time we fall.
生命中最大的荣耀不在于从未跌倒,而在于每次跌倒后都能重新站起来。
动态规划的初步理解
什么是动态规划?最直白的理解就是动态的规划。
那高级一点的理解呢?就是每时每刻都拿着一个小本本,也就是记事本,把干的事情都记录下来,不断规划自己的策略,这就是动态规划。
动态规划里的小本本就对应着程序里的数组,而策略不就是往里依次填值吗。
动态规划理解到这,恭喜你,你已经了解了动态规划了。简单吧!
那我们边讲题,边理解!
动态规划我们一般用dp来表示。
求最短路径数
问从A(1,1)走到B(n,m)有几种最短路径(每次只能向相邻的格子走一格)?
要求:输入B的行坐标(n)和列坐标(m),输出最短路径总数
这题咋一看,毫无头绪,是嵌套for循环?还是while?都不是,是DP,你看:
假设输入的是2和3,那么先把格子画出来,是这样的。

那每个格子里该填什么呢?对了,应该填到当前格子的最短路径数。那是不是每个格子都要从头输一遍呢?你仔细想想,题目说要最短,那走回头路肯定不行,那只能往下走或者右走,这样才能确保最短。因此每一格的最短路径数,不就是它上面的格子+左边的格子吗?
知道了DP公式,那好做了。
填完就是这样的,你可以验证一下:

最后输出dp[n][m]就完事了,上代码:
#include<bits/stdc++.h>using namespace std;int main(){int n,m,dp[505][505];memset(dp,0,sizeof(dp)); cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(i==1&&j==1) dp[i][j]=1;//第一个格子只有一条路径 else{dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}cout<<dp[n][m]<<endl;return 0; }洛谷 P1002 过河卒
网址:[NOIP2002 普及组] 过河卒 - 洛谷
题目描述
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0,0)、B 点 (n,m),同样马的位置坐标是需要给出的。
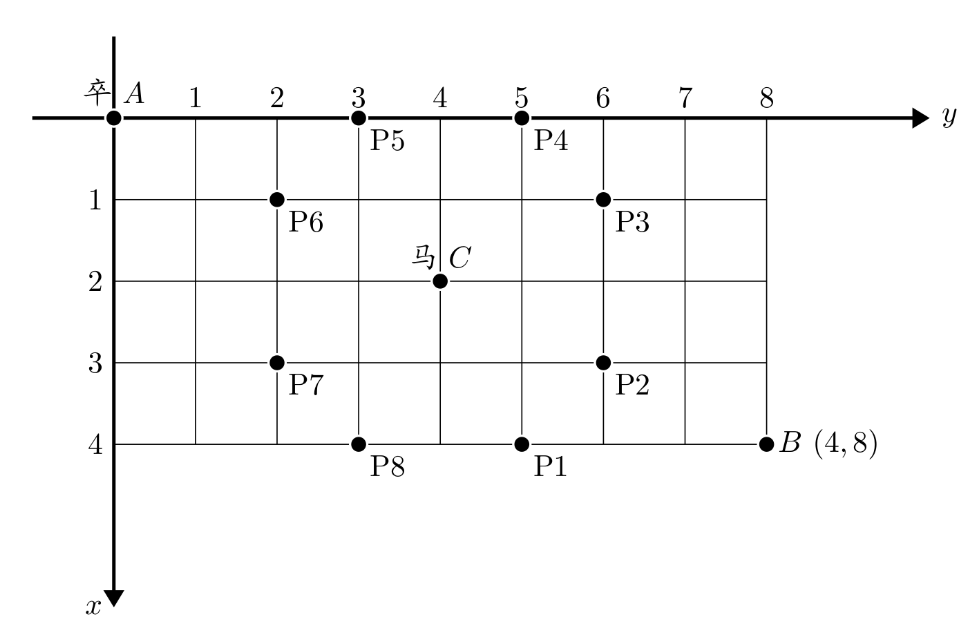
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入样例
6 6 3 3输出样例
6思路
这题看上去不就是DFS吗,简简单单直接提交,可是……
成功的超了时,那咋办,对了之前我不是讲过DP吗,没看的回我主页看看。这题数据较大,用DP不快吗?
那DP公式是啥呢?这里需要用到象棋知识,当卒过河后是不能向后走的,那么DP数组的每一格就是他上一格的路径数+左边一格的路径数(这个和我讲的DP特别像,不理解的去看我的DP文章)。当然马能拦住的地方开始都得给他设成不能走。
那代码不就So Easy了吗,上代码:
AC Code
#include<iostream>#include<algorithm>using namespace std;long long dp[30][30];int dx[8]={-2,-2,-1,-1,1,1,2,2},dy[8]={1,-1,2,-2,2,-2,1,-1};//马跳的坐标变化int main(){ int n,m,x,y; cin>>n>>m>>x>>y; n+=1;m+=1;x+=1;y+=1; for(int i=0;i<8;i++){ int nx=x+dx[i]; int ny=y+dy[i]; if(nx>=1&&nx<=n&&ny>=1&&ny<=m) dp[nx][ny]=-1; } dp[1][0]=1; dp[x][y]=-1; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(dp[i][j]==-1) dp[i][j]=0; else{ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } } cout<<dp[n][m];return 0;}