欢迎来到 Claffic 的博客 ???
前言:
上一期给大家讲了树的基本概念和特点,现在可以试着回忆一下树的样子,还有一些关系称谓。那么今天要讲的,是二叉树,是一种特殊且实用的树,是不是有些小期待呢!
目录
?1.什么是二叉树
1.1二叉树的结构
1.2满二叉树
1.3完全二叉树
1.4二叉树的性质
?2.二叉树的存储结构
2.1顺序存储
2.2链式存储
1.什么是二叉树
1.1二叉树的结构
先来回顾下树:倒置的,根在顶端,向下分岔... ...
所谓二叉树,二叉嘛,就是有两个叉子呗:
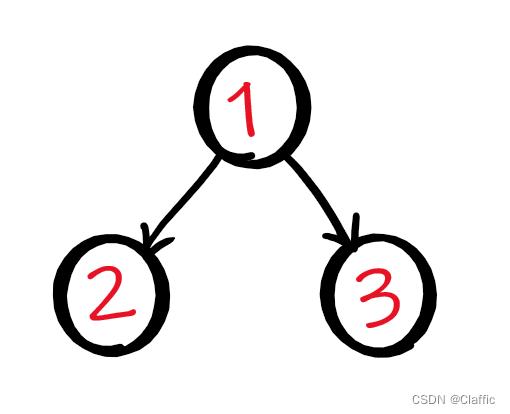
一颗简单的二叉树
还真是,简单说,它就是每个结点最多能分两个叉的树。
一棵二叉树是结点的一个有限集合:
• 或者为空 • 由一个根节点加上两棵别称为左子树和右子树的二叉树组成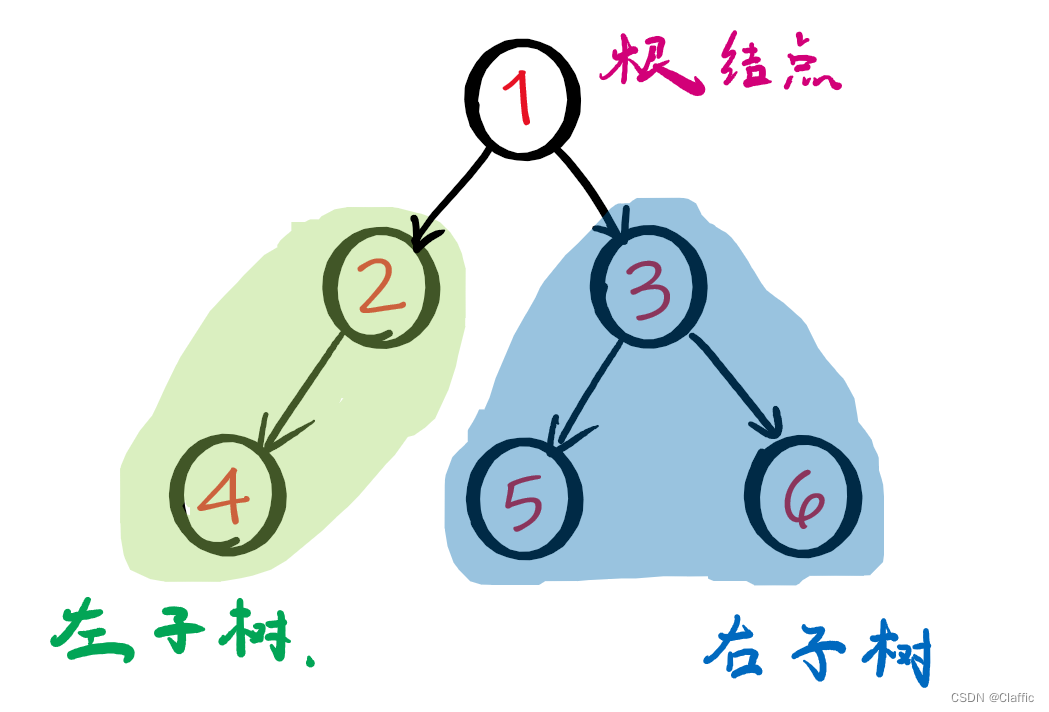
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
那么二叉树是不是只有二叉的情况呢?
其实并不是,下面总结二叉树的几种单元形态:
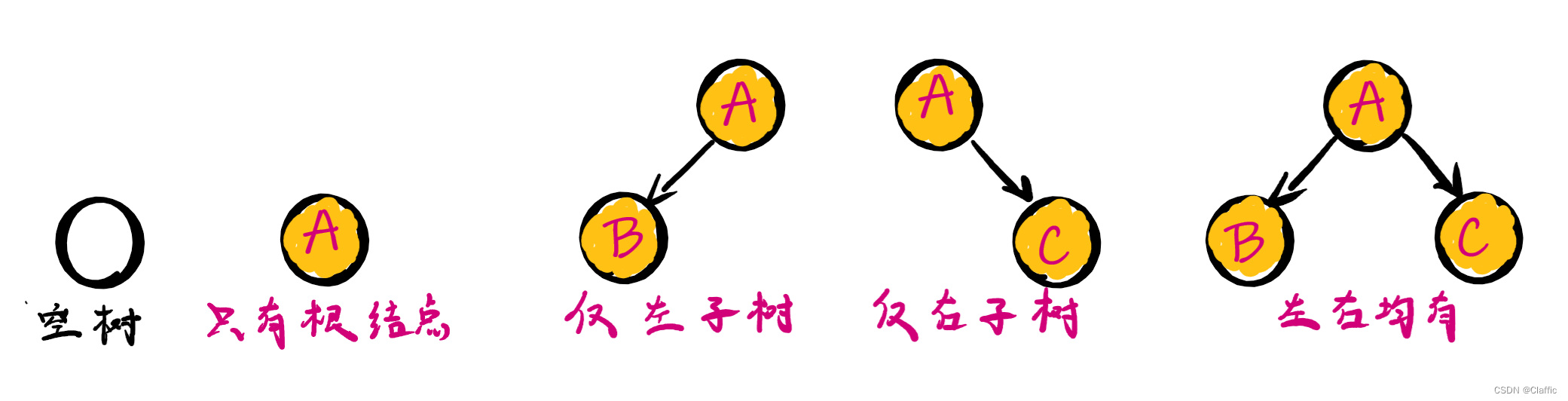
任意一种二叉树都可以由上面的形态复合而成。
1.2满二叉树
这是一种特殊的二叉树
满,意味着除根节点以外的结点都拥有左右结点(子树),即每一层的结点数达到最大值。
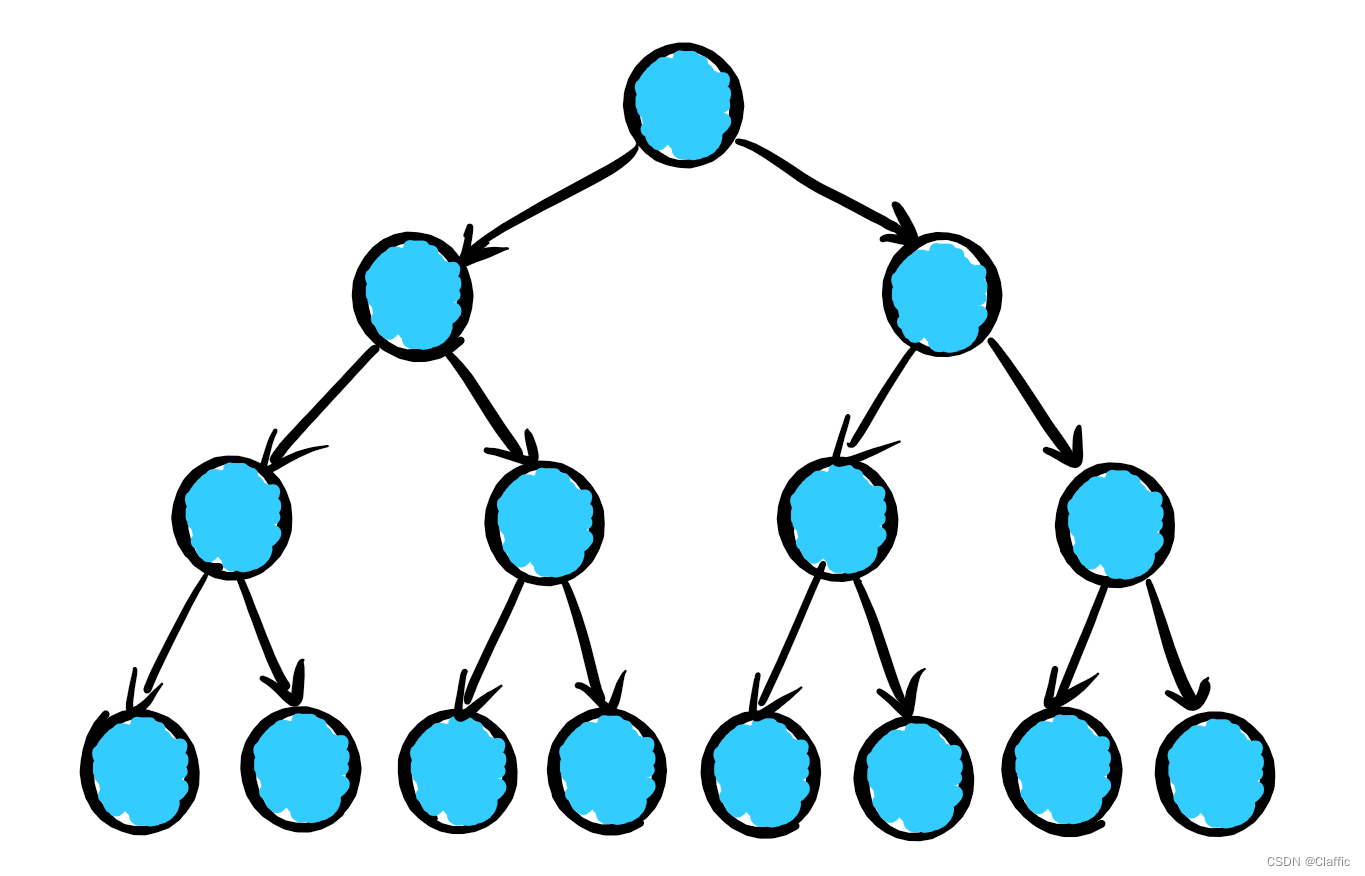
例:满二叉树
非常完美的二叉树~
如果设它的高度为K,那么它共有2^K-1个结点,同样可以用这条性质来判断是否为满二叉树。
1.3完全二叉树
这种树相比满二叉树就有些空缺了,
但是空的结点也有讲究:
从二叉树末端(右下角)开始,空到这一层的任意位置,保证空结点不间断。
换句话说,最后一层的结点都仅靠左部。
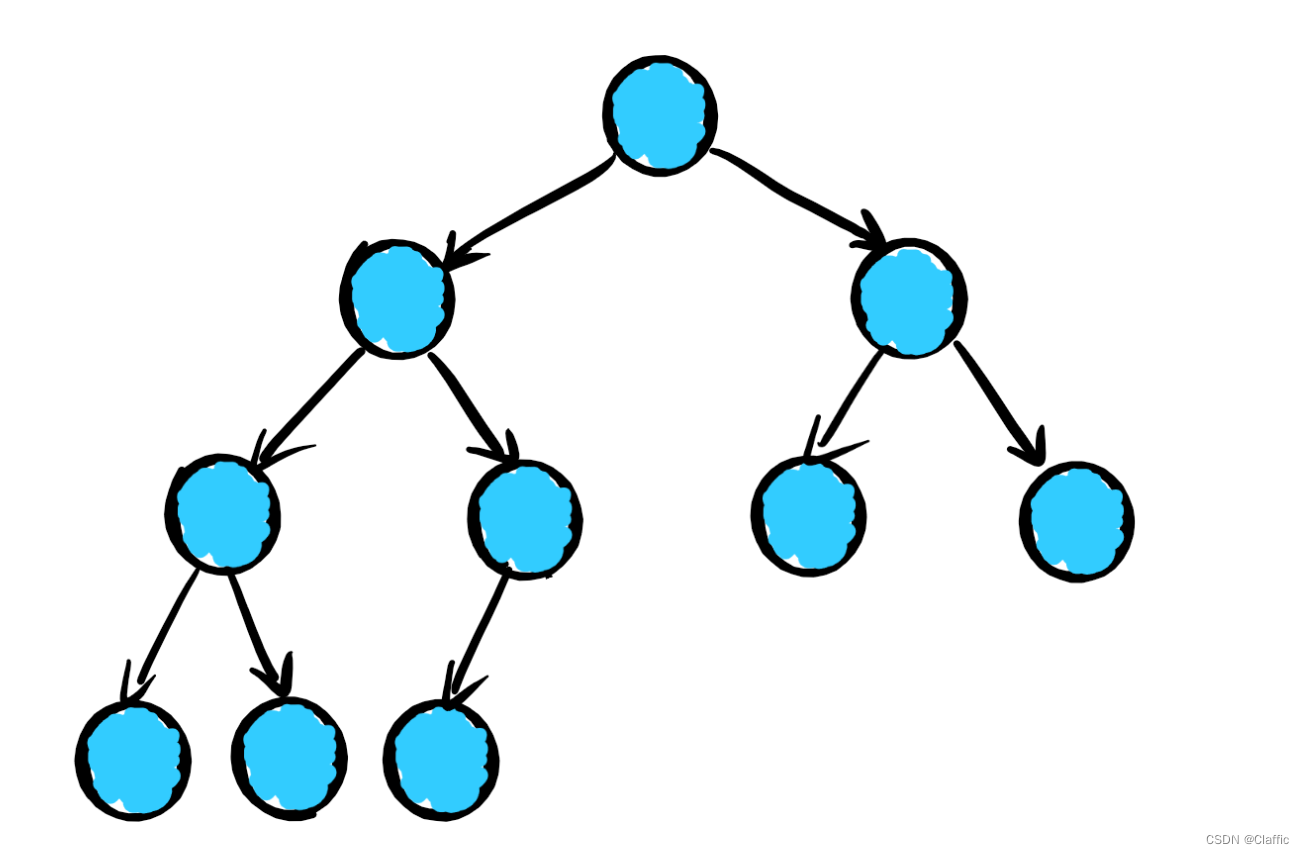
例:完全二叉树
它的准确的定义是:
对于深度为 K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点。要注意:满二叉树是一种特殊的完全二叉树,完全二叉树的范围更广一些。
1.4二叉树的性质
• 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2^(i-1) 个结点。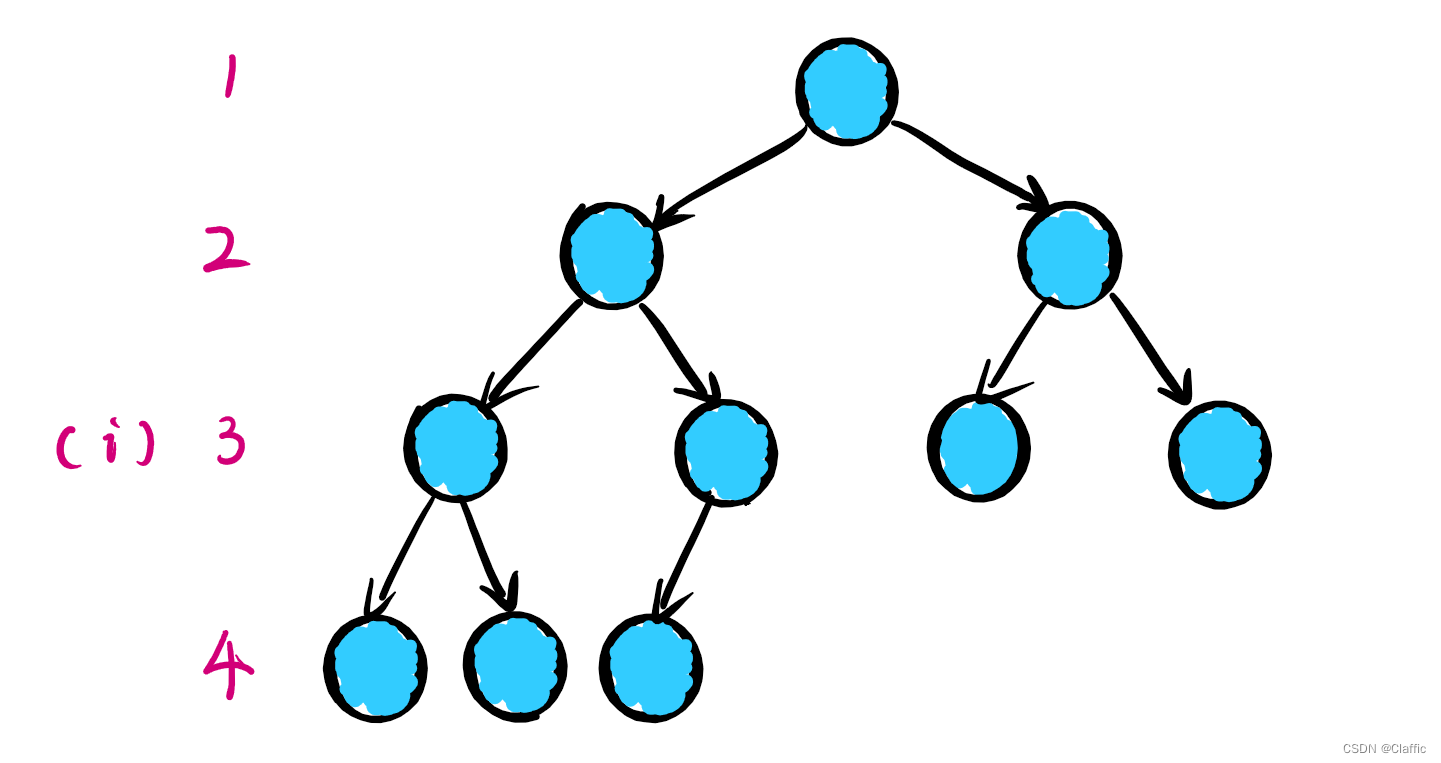
最多就是满的情况,层的编号与每层最多结点的个数关系:Ni = 2^(i-1);
可以联想一下有丝分裂... ...
• 若规定根节点的层数为1 ,则 深度为 h 的二叉树的最大结点数是2^h-1这里就是一个等比数列求和,
在完全二叉树的情况下,第一层到第h层的结点个数:
2^0,2^1,2^2,2^3,... ... 2^(h-1)
求和:
Nh = 2^0+2^1+2^2+2^3+...+2^(h-1)
通过错位相减求和得到结点总数:
Nh = 2^h-1
• 对任何一棵二叉树, 如果度为 0 其叶结点个数为n0 , 度为 2 的分支结点个数为n2 , 则有 n0 = n2+ 1这个可以简单找找规律:
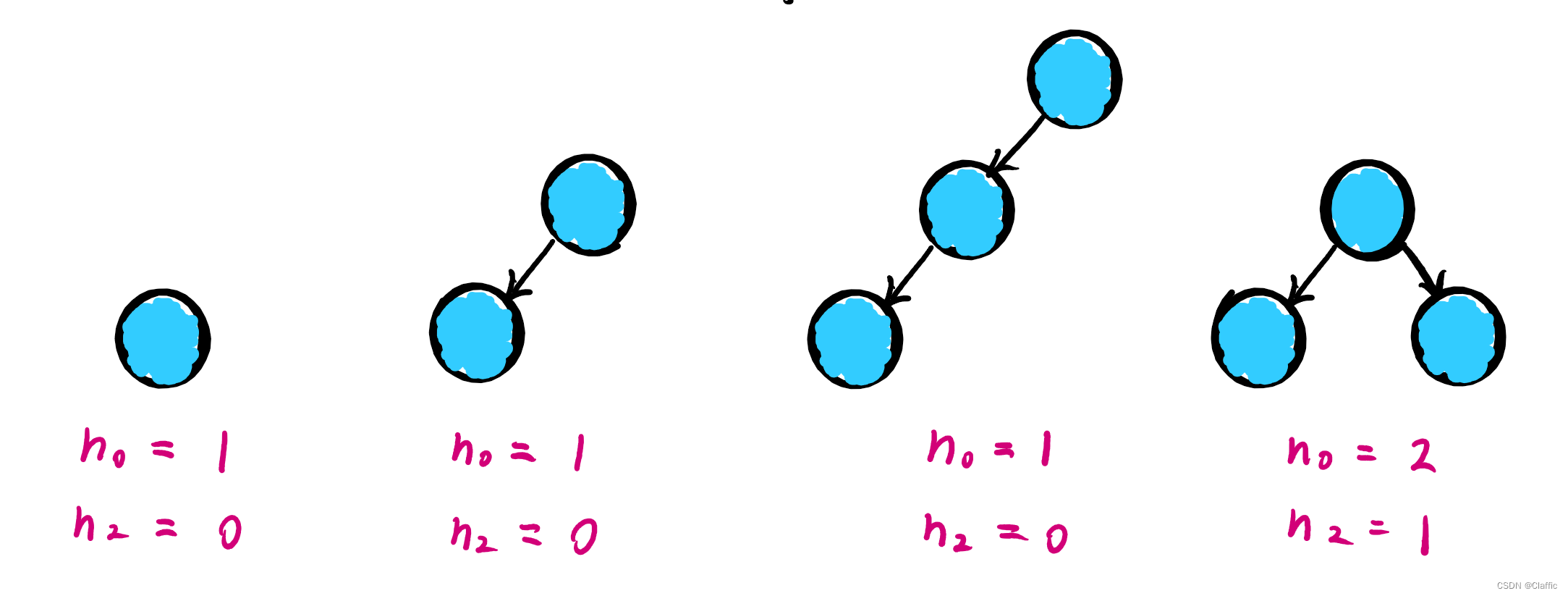
可以发现叶子结点的个数总比度为2的结点个数多1
• 若规定根节点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h = log2(n+1) 【log2(n+1)是以2为底,n+1的对数】其实就是按之前求最大个数的式子 Nh = 2^h-1 把h表示出来,一个意思
• 对于具有n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有: 若 i>0 , i 位置节点的双亲序号: (i-1)/2 ; i=0 , i 为根节点编号,无双亲节点 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子可以看看这个标记:
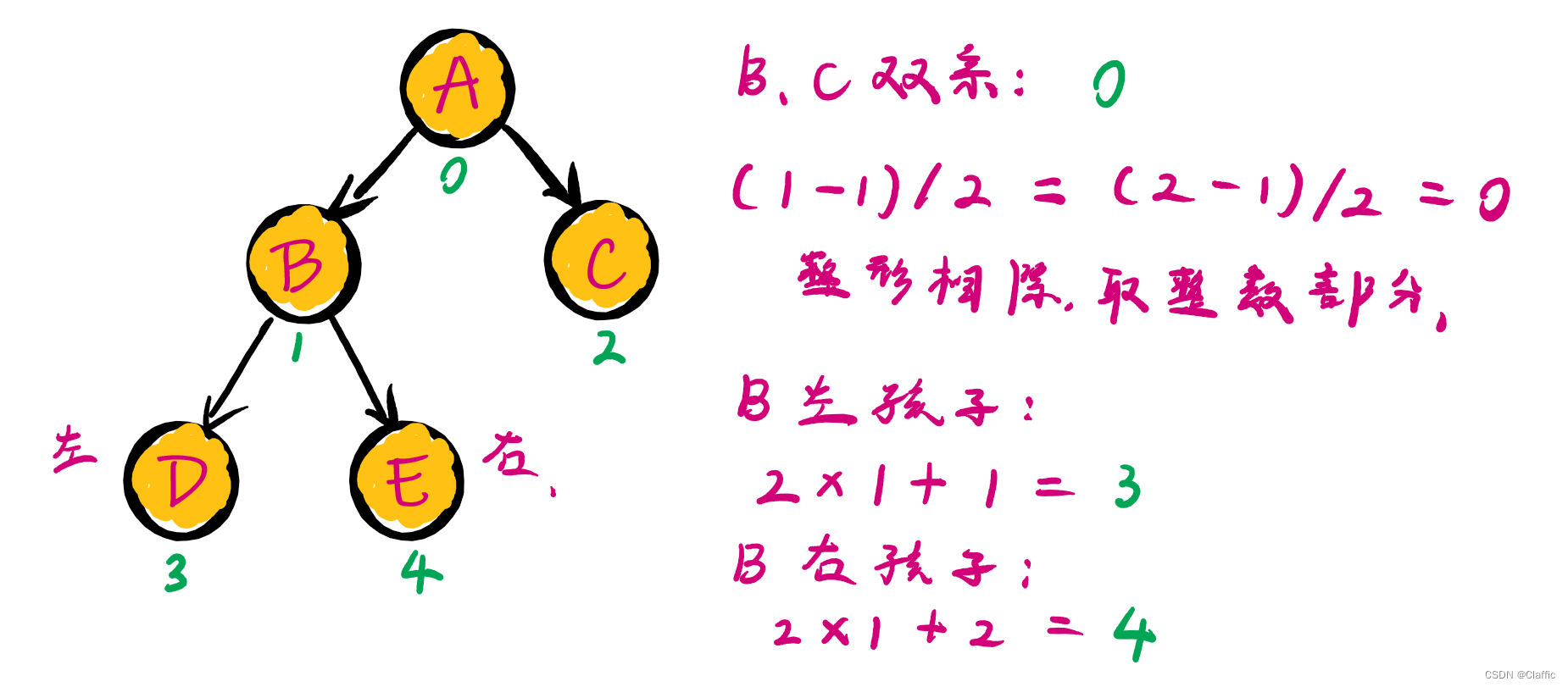
2.二叉树的存储结构
2.1顺序存储
所谓顺序存储,就是以数组来实现二叉树。
欸?用数组来实现二叉树,
其实这个跨度还蛮大的,心里想的是链型的,实际实现却是用数组这种顺序结构。
这里用 逻辑结构 和 物理结构 来分别表示:
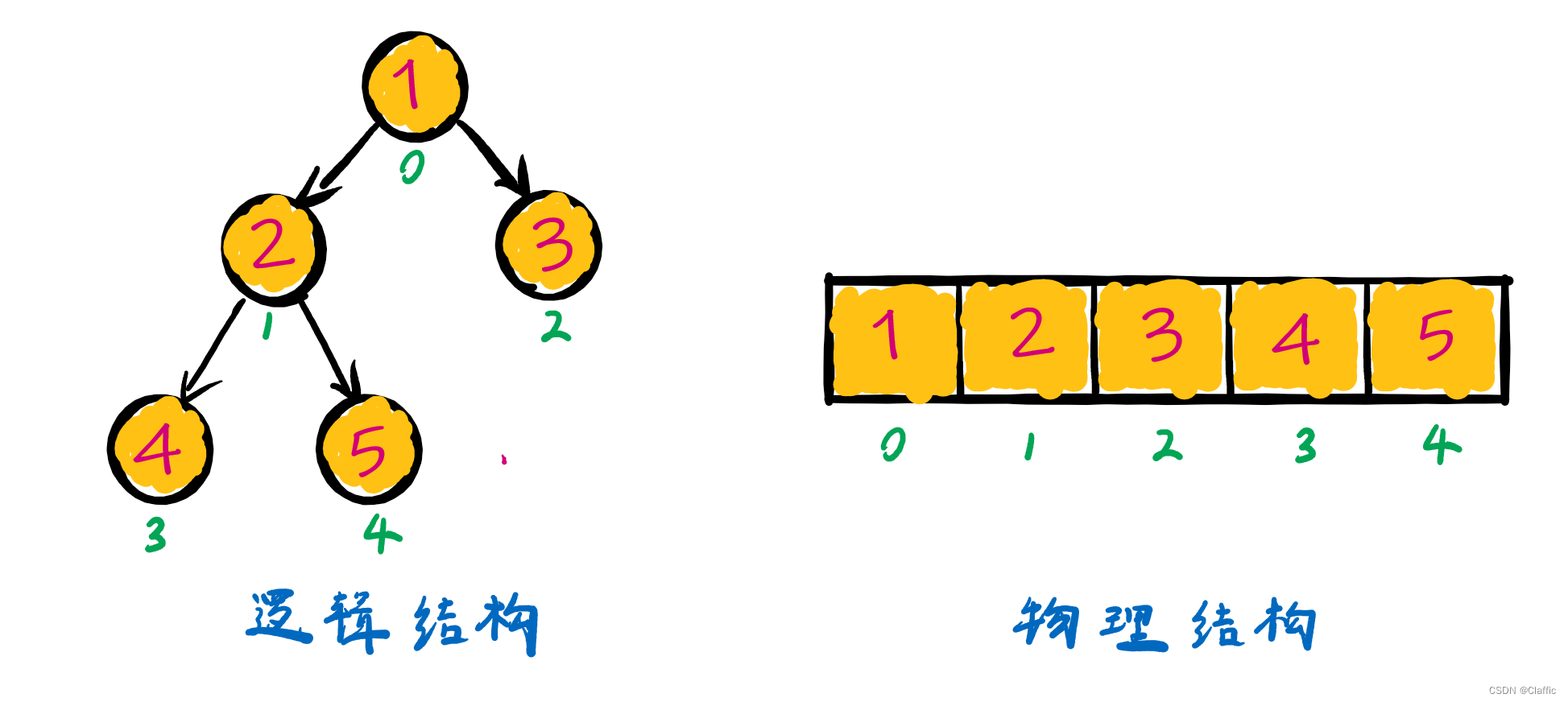
逻辑结构就是心里想的,物理结构就是实际实现需要的
这种存储结构适用于满二叉树,因为满二叉树不会有数组空间的浪费。
顺序存储中有一个典型的数据结构叫做堆(一种二叉树,此堆非彼堆,彼堆是操作系统中管理内存的一块区域分段),这里放到下期讲解。
2.2链式存储
这个链式存储就是正常的思路了:
typedef int BTDataType;typedef struct BinaryTreeNode{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}BTNode;这里定义一棵二叉树树的基本结构:
要存储的数据,指向左子树的指针,指向右子树的指针。
所以根据左右孩子的关系就可以创建一颗二叉树:
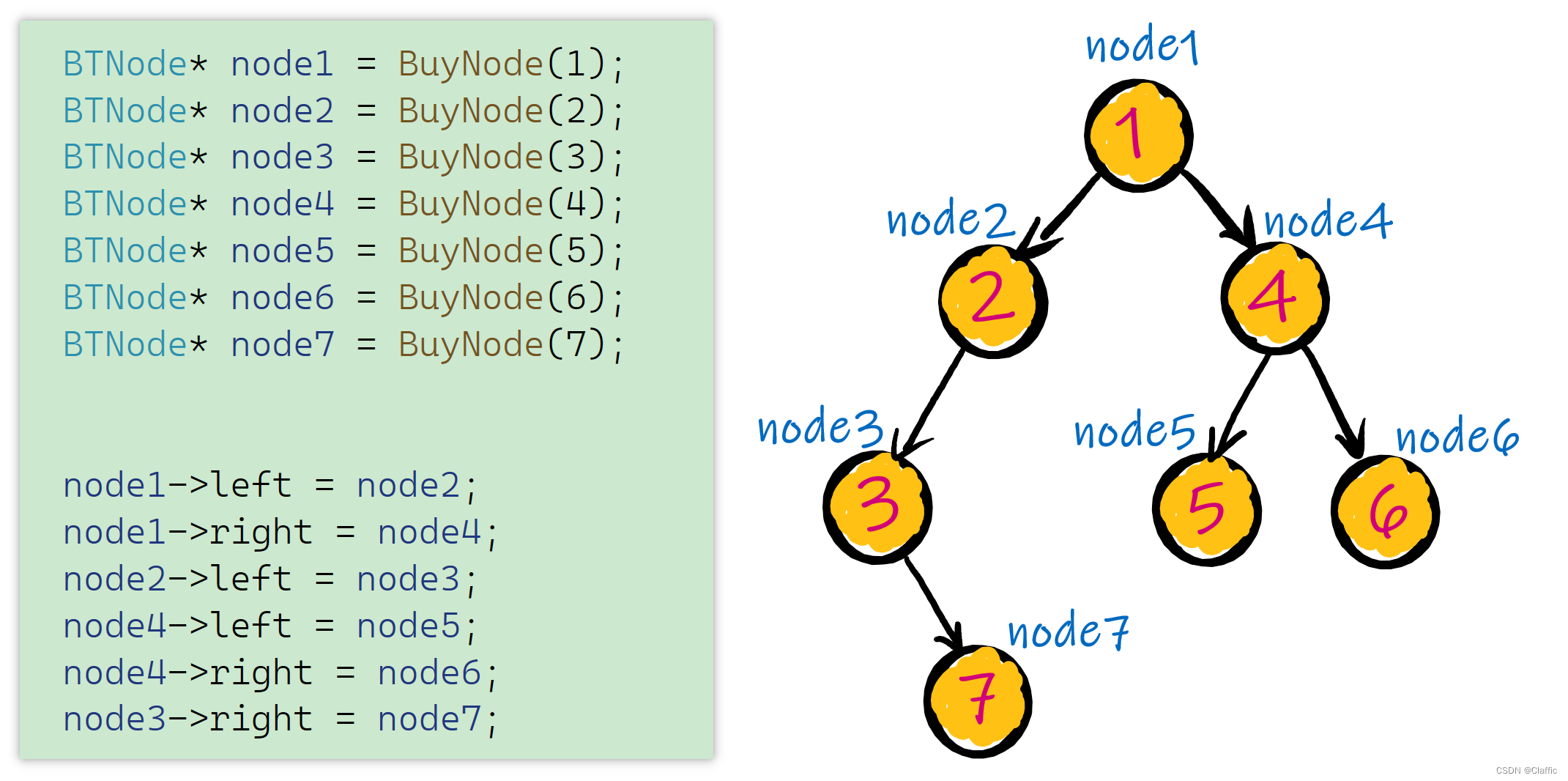
根据左右孩子关系创建的一颗简单二叉树
链式结构方便在遍历,后期会讲解二叉树的遍历。
总结:
这篇博客给大家介绍了二叉树,更加偏向理论层面,那么下期就会带大家敲代码实现一些特殊的二叉树:堆,二叉树的遍历等等。
码文不易
如果你觉得这篇文章还不错并且对你有帮助,不妨支持一波哦 ???