文章目录
?前言?2012年及以前蓝桥杯大赛历届真题(共14题)1434 蓝桥杯历届试题-回文数字【简易法判断回文】 ?第四届1205. 买不到的数目 ?第十届Fibonacci 数列与黄金分割修改数组等差数列成绩分析 ?第十二届时间显示 ?十三届统计子矩阵李白打酒李白打酒加强版 ✨精选递增三元组 - 空间换时间日志统计 -滑动窗口扫雷 - 模拟美丽的区间 - 双指针数位之和 - 模拟统计选数异或 - DPX 图形 - DFS时长计算 - 时分秒回文日期付账问题 - 贪心 ?填空蛇形填数 - 模拟补充类似题[756. 蛇形矩阵]棋盘放麦子质数 - 线性筛法猜生日含 2 天数 - 日期模拟 - 国赛填算式 - 国赛国王的遗产本质上升序列天干地支 - 国赛卡片 - 统计跑步锻炼 - 日期最大子矩阵最小公倍数平方和拆分平方和分数
?前言
?本文包含去年刷题部分,按历年题目之间的联系进行整理,挖掘共性,可能下一场比赛中也会出现类似思路的改进,希望帮大家挖到点上
根据蓝桥杯大赛独特性,尤其填空部分具有颇具特色的解题技巧和输入输出的常规写法的掌握
❗️填空题须知:填写答案(数字或者字符或者代码补充[很少])不用写代码也不用printf,任何与答案不同写法的均算错误!
建议采用暴力枚举,在计算机跑出答案后填写答案,相当于没有时间约束,只看最后的答案是否正确
如果对您有帮助的话还请动动小手 点赞? 收藏⭐️ 关注❤️
蓝桥杯历届真题刷题C语言网 【小技巧:可改page=?快速跳转】
?2012年及以前蓝桥杯大赛历届真题(共14题)
1434 蓝桥杯历届试题-回文数字【简易法判断回文】
时间限制: 1Sec 内存限制: 128MB
题目描述
观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
本题要求你找到一些5位或6位的十进制数字。满足如下要求:
该数字的各个数位之和等于输入的整数。
输入格式
一个正整数 n (10< n< 100), 表示要求满足的数位和。
输出格式
若干行,每行包含一个满足要求的5位或6位整数。
数字按从小到大的顺序排列。
如果没有满足条件的,输出:-1
样例输入
44
样例输出
99899
499994
589985
598895
679976
688886
697796
769967
778877
787787
796697
859958
868868
877778
886688
895598
949949
958859
967769
976679
985589
994499
佬の链接简短判断回文: 如果把最低位放到最高位,秦九昭过程:等效翻转 ==> 若翻转数值相同则为回文串编写细节:i保持循环顺序不能改变i的值, 需取临时t=i判断条件
举个反例:123:123%10=3 -> 123/10=12 -> 310+12%10=32 -> 12/10=1 ->3210+1%10=321;
则123 != 321 故不是回文数;
求个位数字之和只用在求回文得时候 每次取余得到得数累加求和即可【秦九昭】。
#include <cstdio>using namespace std;int main(){ int n; bool flag = false; scanf("%d", &n); for(int i = 10000; i < 1000000; ++i) { int t = i, num = 0, sum = 0;//重点:取临时t判断, 不能改变i的值影响遍历 while(t) { num = num * 10 + t % 10;// 简短判断回文: 如果把最低位放到最高位,秦九昭过程:等效翻转 ==> 若翻转数值相同则为回文串 sum += t % 10; t /= 10; } if(num == i && sum == n) { flag = true; printf("%d\n", i); } } if(!flag) puts("-1"); return 0;}?第四届
1205. 买不到的数目
时/空限制:1s / 64MB
小明开了一家糖果店。
他别出心裁:把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。
大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式
两个正整数 n,m,表示每种包装中糖的颗数。
输出格式
一个正整数,表示最大不能买到的糖数。
数据范围
2≤n,m≤1000,
保证数据一定有解。
输入样例:
4 7
输出样例:
17
dfs暴力标记或者小学数论
佬の解答:https://www.acwing.com/solution/content/7101/
算法分析:
引理:给定a,b, 若&d = gcd(a,b) > 1&,则一定不能凑出最大数
结论:
如果 a,b均是正整数且互质,那么由 ax+by, x≥0, y≥0 不能凑出的最大数是 ( a − 1 ) ( b − 1 ) − 1 (a−1)(b−1)−1 (a−1)(b−1)−1
打表找规律方法:
#include <iostream>using namespace std;//给定一个m,是否能用p和q凑出来bool dfs(int m,int p,int q){ if(m == 0) return true; if(m >= p && dfs(m - p,p,q)) return true; if(m >= q && dfs(m - q,p,q)) return true; return false;}int main(){ int p,q; cin >> p >> q; int res = 0; for(int i = 1; i <= 1000;i ++) { if(!dfs(i,p,q)) res = i; } cout << res << endl; return 0;}小学数二结论题:
//小学数二结论题(证明略):若两个整数p、q互质 ,则p,q不能凑出的最小整数为 (p - 1)*(q - 1) - 1; #include <iostream>using namespace std;int n,m;int main(){ cin >> n >> m; cout << (n - 1) * (m - 1) - 1 << endl; return 0;}?第十届
Fibonacci 数列与黄金分割
时间限制: 1Sec 内存限制: 128MB
题目描述
Fibonacci 数列是非常著名的数列:
F[1] = 1,
F[2] = 1,
对于 i > 3,F[i] = F[i − 1] + F[i − 2]
Fibonacci 数列有一个特殊的性质,前一项与后一项的比值,F[i]/F[i + 1], 会趋近于黄金分割。
为了验证这一性质,给定正整数 N,请你计算 F[N]/F[N + 1],并保留 8 位 小数。
输入格式
一个正整数 N。(1 ≤ N ≤ 2000000000)
输出格式
F[N]/F[N + 1]。答案保留 8 位小数。
样例输入
2
样例输出
0.50000000
枚举范围太大,观察发现20项之后,8位小数精度都一样!!! #include <bits/stdc++.h>using namespace std;double fib(int n) { long long f[n + 1]; f[1] = 1; f[2] = 1; for (int i = 3; i <= n; ++i) { f[i] = f[i - 1] + f[i - 2]; } return f[n];}int main() { ios::sync_with_stdio(false); //cin.tie(NULL); int n; cin >> n; //cout << fixed << setprecision(8) << fib(n) / fib(n + 1) << endl; if (n < 20) printf("%.8lf\n",(double)fib(n)/(double)fib(n+1)); else cout << "0.61803399" << endl; return 0;}ios::sync_with_stdio(false);这条语句关掉scanf 和cin 的同步加快效率。但是即使是这样cin 还要慢 5倍左右,而且一旦使用了这条语句,scanf和cin 混用可能就会造成一些奇怪的问题。
修改数组
时间限制: 1Sec 内存限制: 128MB 提交: 5491 解决: 1348
题目描述
给定一个长度为 N 的数组 A = [A1, A2, · · · AN ],数组中有可能有重复出现 的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A2,A3,··· ,AN。
当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则 小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直 到 Ai 没有在 A1 ∼ Ai−1 中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。 现在给定初始的 A 数组,请你计算出最终的 A 数组
输入格式
第一行包含一个整数 N。 第二行包含N个整数A1,A2,··· ,AN
对于 80% 的评测用例,1 ≤ N ≤ 10000。
对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
输出格式
输出N个整数,依次是最终的A1,A2,··· ,AN。
样例输入
5
2 1 1 3 4
样例输出
2 1 3 4 5
并查集思路:
首先我们每输入一个数,都会判断前面是否已经有过,如果有过就会+1,知道前面没有重复的数。
那么像不像并查集的指向呢,如果没有用过就是自己就是一个集合,根节点指向自己
如果已经用过了,只要将其父节点指向比他大1的节点(此时不重复)就可以。
#include<bits/stdc++.h>using namespace std;const int N = 1000010;int p[N];//查找祖宗节点+路径压缩int find(int x ){ if(p[x] != x) p[x] = find(p[x]); return p[x];}int main(){ int n; cin>>n; for(int i = 0; i < N; i++) p[i] = i; for(int i = 0; i < n; i++) { int x; scanf("%d",&x); x = find(x); printf("%d ",x); p[x] = x+1; } return 0;}等差数列
时间限制: 1Sec 内存限制: 128MB 提交: 7792 解决: 1804
题目描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一 部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有 几项?
输入格式
输入的第一行包含一个整数 N。 第二行包含N个整数A1,A2,···,AN。(注意A1 ∼AN并不一定是按等差数
列中的顺序给出)
(对于所有评测用例,2≤ N ≤100000,0≤ Ai ≤109。)
输出格式
输出一个整数表示答案
样例输入
5
2 6 4 10 20
样例输出
10
题解
乱序先排序,所有相邻两项差的最大公因数, 最大公因数即为 :最大公差d
#include <bits/stdc++.h>using namespace std;const int N = 100000;int a[N];int gcd(int a,int b) {if(b == 0)return a;return gcd(b,a%b);}int main(){ int n; scanf("%d",&n); for(int i=0;i<n;i++){ scanf("%d",&a[i]); } sort(a,a+n); //找最小差值的公约数是公差d; int min=a[0],max=a[n-1]; int d=(a[1]-a[0]); for(int i=2;i<n;i++){ if((a[i+1]-a[i])<=d){//此处d不能换成a[i]-a[i-1]。 d=gcd(d,a[i]-a[i-1]);//求d与其他差值的公差,赋值 } } if(d==0){ printf("%d",n); }else{ printf("%d",(max-min)/d+1); }}成绩分析
题目描述
小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是一个 0 到 100 的整数。
请计算这次考试的最高分、最低分和平均分。
输入描述
输入的第一行包含一个整数 n ( 1 ≤ n ≤ 1 0 4 ) n\ (1 ≤ n ≤ 10^4) n (1≤n≤104) ),表示考试人数。
接下来 n 行,每行包含一个 0 至 100 的整数,表示一个学生的得分。
输出描述
输出三行。
第一行包含一个整数,表示最高分。
第二行包含一个整数,表示最低分。
第三行包含一个实数,四舍五入保留正好两位小数,表示平均分。
输入输出样例
示例
输入
780925674889910输出
991071.29#include<bits/stdc++.h> //送分题using namespace std;const int N = 1e4 + 10;int n;int a[N];double sum;signed main(){ cin >> n; for(int i = 0; i <= n ; i ++) cin >> a[i] , sum += a[i]; sort(a, a + n); printf("%d\n%d\n%.2lf", a[n - 1], a[0], sum / n); // cout << *max_element(a + 1 , a + 1 + n) << endl; // cout << *min_element(a + 1 , a + 1 + n) << endl; // cout << setprecision(2) << fixed << 1.0 * sum / n << endl; return 0;}?第十二届
时间显示
题目描述
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入描述
输入一行包含一个整数,表示时间。
输出描述
输出时分秒表示的当前时间,格式形如 HH:MM:SS,其中 HH 表示时,值为 00 到 23,MM 表示分,值为 00 到 59,SS 表示秒,值为 0 到 59。时、分、秒 不足两位时补前导 0。
输入输出样例
示例 1
输入
46800999输出
13:00:00示例 2
输入
1618708103123输出
01:08:23评测用例规模与约定
对于所有评测用例,给定的时间为不超过 1 0 18 10^{18} 1018 的正整数。
#include <iostream>using namespace std;typedef long long LL; //1e18int main(){ LL n; cin >> n; n = n / 1000; //转换成秒 n %= 86400; //一天内的偏移量 int h = n / 3600, m = n % 3600 / 60, d = n % 60; printf("%02d:%02d:%02d\n", h, m, d); return 0;}?十三届
刷题链接整理
蓝桥杯往界真题OJ在线刷题
统计子矩阵
时间限制: 1Sec 内存限制: 256MB 提交: 908 解决: 147
题目描述
给定一个 N × M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 × 1,最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数,代表矩阵 A.
输出格式
一个整数代表答案。
样例输入
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
样例输出
19
提示
满足条件的子矩阵一共有 19,包含:
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
对于 30% 的数据,N, M ≤ 20. 对于 70% 的数据,N, M ≤ 100.
对于 100% 的数据,1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.
如果直接用 前缀和 + 暴力,复杂度将是O(n4),必须优化
优化的方法是:
1)枚举子矩阵的 左边界i 和 右边界j,
2)用 快指针t 枚举 子矩阵的下边界,慢指针s 维护 子矩阵的上边界 (s ≤≤ t)
3)如果得到的子矩阵的权值和 大于 k,则慢指针s 前进,而子矩阵和必将单调不增
4)慢指针s 继续前进(如图),直到 子矩阵的和 不大于k,慢指针没必要前进了,因为该子矩阵的所有宽度为 j - i + 1 的子矩阵(总共 t - s + 1 种)一定满足要求,更新该情况对答案的贡献 t - s + 1;反之,如果慢指针s越界(s > t),则不操作,直接进入下层循环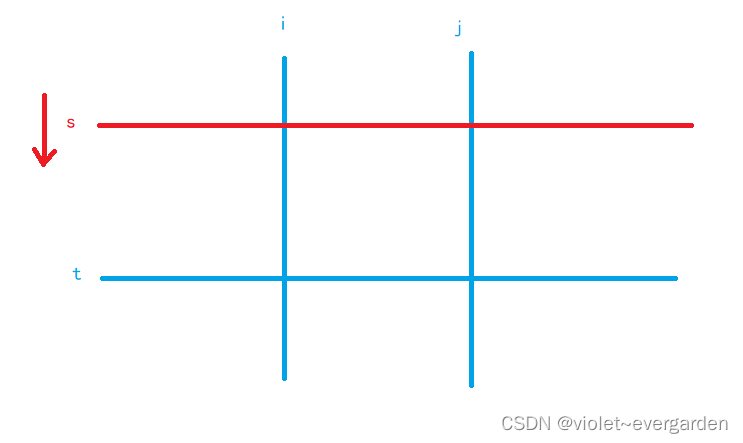
题解
ios::sync_with_stdio(false); 【专用c++の选手】记 ios::sysn_with_stdio ,没有特殊格式输出就用cin和cout 初始化直接存二维前缀和 : a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];【极简初始前缀和】 : a[i][j] += a[i - 1][j] 不用原数组,直接覆盖
#include <cstdio>using namespace std;typedef long long LL;const int N = 510;int n, m, K;int s[N][N]; int main(){ scanf("%d%d%d", &n, &m, &K); for (int i = 1; i <= n; i ++ ) for (int j = 1; j <= m; j ++ ) { scanf("%d", &s[i][j]); //边读入边覆盖((不需要用原数组) s[i][j] += s[i - 1][j]; //前缀和初始化【极简版】 } LL res = 0; for (int i = 1; i <= n; i ++ )//i, j就当做上up与下down边界枚举 for (int j = i; j <= n; j ++ ) for (int l = 1, r = 1, sum = 0; r <= m; r ++ ) { sum += s[j][r] - s[i - 1][r]; while (sum > K) // 超过了:缩小左右边界 : l ++ { sum -= s[j][l] - s[i - 1][l]; //删去子矩阵的边界L一列,上下边界限制为[i, j] l ++ ; } //[l-1,r]不满足, [l, r]刚好满足, 则截取[l, r]范围内更小的左右边界的子矩阵均满足 < k res += r - l + 1; //长度大小: 1 ~ R-L 均满足 即在[l, r]共有 r - l + 1种长度满足 } printf("%lld\n", res); return 0;}暴力6重循环(TLE): 枚举上下左右边界练习for(int u = 1; u <= m; u++) //up 与 down for(int d = u ; d <= m; d++) for(int l = 1; l <= n; l++) for(int r = l; r <= n; r++) { //check(是否子矩阵元素和 >= k) 子矩阵元素和sum = s[r][d] - s[l - 1][d] -s[r][u - 1] + s[l][u] 左上坐标(l,u)和右下左边(r,d)】 }// 接近TLE// #include <bits/stdc++.h> //前缀和+暴力枚举O($n^4$) // using namespace std;// typedef long long LL;// const int N=510;// LL a[N][N],s[N][N],cnt,n,m,k;// inline LL sum(int x1,int y1,int x2,int y2) //内联函数// {// return s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];// }// int main()// {// scanf("%lld%lld%lld",&n,&m,&k);// for(int i=1;i<=n;i++)// {// for(int j=1;j<=m;j++)// {// scanf("%lld",&a[i][j]);// s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];// }// }// for(int l=1;l<=m;l++)//枚举矩阵的左边// {// for(int r=l;r<=m;r++)//枚举矩阵的右边 【枚举所有[l, r]】// {// for(int i=1,j=1;i<=n;i++)//从上到下双指针扫描 // {// while(j <= i && sum(j,l,i,r) > k) j++;// if(j<=i) cnt+=(i-j+1);//有可能最小的矩阵都不满足,此时j>i// }// }// }// printf("%lld",cnt);// return 0;// }李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。 逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花 1010 次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为 aa,遇花记为 bb 。则:babaabbabbabbbbbabaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
#include <iostream>using namespace std;int f[10][10][200];int main(){ f[0][0][2] = 1; for (int i = 0; i <= 5; i ++ ) //遇到i个店j朵花且有k单位酒的方案 for (int j = 0; j <= 10; j ++ ) for (int k = 0; k <= 10; k ++ ) { int &v = f[i][j][k]; if(i && k % 2 == 0) v = v + f[i - 1][j][k / 2]; if(j) v = v + f[i][j - 1][k + 1]; } printf("%d", f[5][9][1]); return 0;}李白打酒加强版
话说大诗人李白,一生好饮。
幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2
斗。
他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N
次,遇到花 M
次。
已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒 (0
斗) 时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入格式
第一行包含两个整数 N
和 M
。
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007
的结果。
数据范围
对于 40%
的评测用例:1≤N,M≤10
。
对于 100%
的评测用例:1≤N,M≤100
。
输入样例:
5 10
输出样例:
14
样例解释
如果我们用 0
代表遇到花,1
代表遇到店,14
种顺序如下:
010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100
#include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 110, MOD = 1e9 + 7;int n, m;int f[N][N][N];int main(){ cin >> n >> m; f[0][0][2] = 1; //初始2斗酒 for (int i = 0; i <= n; i ++ ) //遇到i个店j朵花且有k单位酒的方案 for (int j = 0; j <= m; j ++ ) for (int k = 0; k <= m; k ++ ) { int& v = f[i][j][k]; if (i && k % 2 == 0) v = (v + f[i - 1][j][k / 2]) % MOD; //遇到酒店之前一步的状态 : 酒有k/2 (则i>=1 且 k为偶数) if (j) v = (v + f[i][j - 1][k + 1]) % MOD; //遇到花店之前一步的状态 : 酒有k+1 (j - 1 >= 0) } cout << f[n][m - 1][1] << endl; //求最后一步必须是花的方案数 == 上一个状态遇到店N次遇到花M次且酒剩下1 return 0;}✨精选
递增三元组 - 空间换时间
给定三个整数数组
A=[A1,A2,…AN],
B=[B1,B2,…BN],
C=[C1,C2,…CN],
请你统计有多少个三元组 (i,j,k)
满足:
1≤i,j,k≤N
Ai<Bj<Ck
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,…AN。
第三行包含 N 个整数 B1,B2,…BN。
第四行包含 N 个整数 C1,C2,…CN。
输出格式
一个整数表示答案。
数据范围
1≤N≤ 1 0 5 10^5 105
,
0≤Ai,Bi,Ci≤ 1 0 5 10^5 105
输入样例:
31 1 12 2 23 3 3输出样例:
27STL-二分-枚举b[i] 组合A × \times ×C
#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5 + 10;int a[N], b[N], c[N];int main() {int n;scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);for(int i = 0; i < n; i++) scanf("%d", &b[i]);for(int i = 0; i < n; i++) scanf("%d", &c[i]);sort(a, a + n), sort(b, b + n), sort(c, c + n);LL cnt = 0;for(int i = 0; i < n; i++) //b比a大 且 比c小 - 【枚举b[] 乘积 {LL A = lower_bound(a, a + n, b[i]) - a; //a[]中第一个大等于b[i]的位置 (从0开始刚好 个数 == 下标) LL C = n - (upper_bound(c, c + n, b[i]) - c); //c[]中第一个小于b的位置 (剩下均大于b[i]) cnt += A * C;}printf("%lld", cnt);return 0;}三指针
#include <bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1e5 + 10;int a[N], b[N], c[N];int main() {int n;scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);for(int i = 0; i < n; i++) scanf("%d", &b[i]);for(int i = 0; i < n; i++) scanf("%d", &c[i]);sort(a, a + n), sort(b, b + n), sort(c, c + n);LL sum = 0,s1 = 0,s2 = 0; for(int i=0;i<n;i++){ while(s1 < n && a[s1] < b[i]) s1++; while(s2 < n && c[s2] <= b[i]) s2++; sum += s1 * (n - s2); }printf("%lld", sum);return 0;}日志统计 -滑动窗口
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N
行。
其中每一行的格式是:
ts id 表示在 ts 时刻编号 id 的帖子收到一个”赞”。
现在小明想统计有哪些帖子曾经是”热帖”。
如果一个帖子曾在任意一个长度为 D
的时间段内收到不少于 K
个赞,小明就认为这个帖子曾是”热帖”。
具体来说,如果存在某个时刻 T
满足该帖在 [T,T+D)
这段时间内(注意是左闭右开区间)收到不少于 K
个赞,该帖就曾是”热帖”。
给定日志,请你帮助小明统计出所有曾是”热帖”的帖子编号。
输入格式
第一行包含三个整数 N,D,K。
以下 N 行每行一条日志,包含两个整数 ts 和 id。
输出格式
按从小到大的顺序输出热帖 id。
每个 id 占一行。
数据范围
1≤K≤N≤ 1 0 5 10^5 105,
0≤ts,id≤ 1 0 5 10^5 105,
1≤D≤10000
输入样例:
7 10 20 10 1010 1010 19 1100 3100 3输出样例:
13//有重复统计,就有优化【滑动窗口,进去一个+出来一个】#include <cstdio>#include <cstring>#include <iostream>#include <algorithm>#define x first #define y secondusing namespace std;typedef pair<int, int> PII; const int N = 100010;int n, d, k;PII logs[N]; // (ts,id)int cnt[N];bool st[N]; // 记录每个帖子是否是热帖int main(){ scanf("%d%d%d", &n, &d, &k); for (int i = 0; i < n; i ++ ) scanf("%d%d", &logs[i].x, &logs[i].y); sort(logs, logs + n);//按时间排序【!!!】 for (int i = 0, j = 0; i < n; i ++ )//i在前,j在后 [指i先走] { int id = logs[i].y; cnt[id] ++ ; while (logs[i].x - logs[j].x >= d) //if(i位置赞 - j位置赞 >= d时间跨度) j向前移动 【看做滑动窗口理解,窗口大小 = d】 { cnt[logs[j].y] -- ;//j向前移动位置 ,原本的j位置出窗口, i在循环中i++ j ++ ; } if (cnt[id] >= k) st[id] = true;//标记true } for (int i = 0; i <= 100000; i ++ )//遍历所有位置,输出即可 if (st[i]) printf("%d\n", i); return 0;}容器遍历
#include <iostream>#include <cstring>#include <algorithm>#include <set>#define x first#define y secondusing namespace std;const int N = 1e5 + 10;typedef pair<int, int> PII;int n, d, k;int cnt[N];PII logs[N];set<int> ans;int main(){ cin >> n >> d >> k; for (int i = 0; i < n; i ++ ) cin >> logs[i].x >> logs[i].y; sort(logs, logs + n); for (int i = 0, j = 0; i < n; i ++ ){ int id = logs[i].y; cnt[id] ++; while (logs[i].x - logs[j].x >= d){ cnt[logs[j].y] --; ++ j; } if (cnt[id] >= k) ans.insert(id); } for (set<int>::iterator it = ans.begin(); it != ans.end(); it ++ ) cout << *it << endl; return 0;}扫雷 - 模拟
题目描述
在一个 n 行 m 列的方格图上有一些位置有地雷,另外一些位置为空。
请为每个空位置标一个整数,表示周围八个相邻的方格中有多少个地雷。
输入描述
输入的第一行包含两个整数 n, m。
第 2 行到第 n + 1 行每行包含 m 个整数,相邻整数之间用一个空格分隔。如果对应的整数为 0,表示这一格没有地雷。如果对应的整数为 1,表示这一格有地雷。
其中, 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100 分钟后还是在当天。
输出描述
输出 n 行,每行 m 个整数,相邻整数之间用空格分隔。
对于没有地雷的方格,输出这格周围的地雷数量。对于有地雷的方格,输出 9。
输入输出样例
示例 1
输入
3 40 1 0 01 0 1 00 0 1 0输出
2 9 2 19 4 9 21 3 9 2运行限制
最大运行时间:1s
最大运行内存: 128M
#include <iostream>using namespace std;const int N = 110;int g[N][N], f[N][N];int get(int x, int y) { if(g[x][y] == 1) return 9; int res = 0; for(int i = x - 1; i <= x + 1; i++) for(int j = y - 1; j <= y + 1; j++) if(g[i][j] == 1) res ++; return res;}int main(){ int n, m; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++) //从1开始不用判断出界 for(int j = 1; j <= m; j++) scanf("%d", &g[i][j]); for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { f[i][j] = get(i, j); printf("%d " , f[i][j]); } puts(""); } return 0;}美丽的区间 - 双指针
题目描述
给定一个长度为 n 的序列 ,分别表示 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots, a_n a1,a2,⋯,an 和一个常数 S。
对于一个连续区间如果它的区间和大于或等于 S,则称它为美丽的区间。
对于一个美丽的区间,如果其区间长度越短,它就越美丽。
请你从序列中找出最美丽的区间。
输入描述
第一行包含两个整数 n,S,其含义如题所述。
接下来一行包含 n 个整数,分别表示 a 1 , a 2 , ⋯ , a n 1 ≤ N ≤ 1 0 5 , 1 × a i ≤ 1 0 4 , 1 ≤ S ≤ 1 0 8 a_1,a_2,\cdots, a_n \\ 1\leq N \leq 10^5 ,1\times a_i\leq 10^4,1\leq S\leq 10^8 a1,a2,⋯,an1≤N≤105,1×ai≤104,1≤S≤108
输出描述
输出共一行,包含一个整数,表示最美丽的区间的长度。
若不存在任何美丽的区间,则输出 0。
输入输出样例
示例 1
输入
5 61 2 3 4 5输出
2运行限制
最大运行时间:1s
最大运行内存: 128M
#include <iostream>using namespace std;const int N = 1e5 + 10;int n, m;int a[N]; // 表示原数组int s[N]; // 表示前缀和数组int main(){ scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ )//用到下标i-1 ,下标从1开始 { scanf("%d", &a[i]); s[i] = s[i - 1] + a[i];//前缀和数组 } int minv = n; for(int i = 1, j = 1; i <= n; i++) //[i, j] { while(i < n && s[j] - s[i - 1] < m) j++; if(s[j] - s[i - 1] >= m && minv >= j - i + 1) minv = j - i + 1; } if(minv == n) puts("0"); else cout << minv << endl; return 0;}数位之和 - 模拟统计
问题描述
小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当 两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。
例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位 之和 13 。
又如, 6 排在 2022 前面, 因为它们的数位之和相同, 而 6 小于 2022 。
给定正整数 n, m, 请问对 1 到 nn 采用这种方法排序时, 排在第 m 个的元 素是多少?
输入格式
输入第一行包含一个正整数 n 。
第二行包含一个正整数 m 。
输出格式
输出一行包含一个整数, 表示答案。
样例输入
135样例输出
3样例说明
1 到 13 的排序为: 1,10,2,11,3,12,4,13,5,6,7,8,9。第 5 个数为 3 。
评测用例规模与约定
对于 30 % 30 \% 30% 的评测用例, 1 ≤ m ≤ n 1 \leq m \leq n 1≤m≤n 。
对于 50 % 50 \% 50% 的评测用例, 1 ≤ m ≤ n 1 \leq m \leq n 1≤m≤n 。
对于所有评测用例, 1 ≤ m ≤ n ≤ 1 0 6 1 \leq m \leq n \leq 10^{6} 1≤m≤n≤106
。
#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 10;int b[N],a[N];//b[N]:存储数位之和;a[i]:排序之前按顺序存储1~n之间的数,排序之后存储此题的解bool cmp(int x,int y){ return b[x] < b[y] || b[x] == b[y] && x < y; //返回数位之和小的, 若数位之和相等则返回值小的}int main(){ int n ,m; cin >> n >> m; //1~n中按规则排序第m大的数 for(int i = 1;i <= n; i++) { int num = i; while(num) b[i] += num % 10, num /= 10; a[i] = i; } sort(a + 1,a + 1 + n, cmp); //按规则排序 cout << a[m] << endl; return 0;}选数异或 - DP
问题描述
给定一个长度为 n 的数列 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A1,A2,⋯,An
和一个非负整数 x, 给定 m 次查 询, 每次询问能否从某个区间 [l, r]中选择两个数使得他们的异或等于 x 。
输入格式
输入的第一行包含三个整数 n, m, x 。
第二行包含 n 个整数 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A1,A2,⋯,An
接下来 m 行,每行包含两个整数 l i , r i l_{i}, r_{i} li,ri
表示询问区间 [ l i , r i ] \left[l_{i}, r_{i}\right] [li,ri]
输出格式
对于每个询问, 如果该区间内存在两个数的异或为 xx 则输出 yes, 否则输出 no。
样例输入
4 4 11 2 3 41 41 22 33 3样例输出
yesnoyesno样例说明
显然整个数列中只有 2, 3 的异或为 1。
评测用例规模与约定
对于 20 % 的评测用例, 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100;
对于 40 % 的评测用例, 1 ≤ n , m ≤ 1000 1 \leq n, m \leq 1000 1≤n,m≤1000;
对于所有评测用例, 1 ≤ n , m ≤ 100000 , 0 ≤ x < 2 20 , 1 ≤ l i ≤ r i ≤ n , 0 ≤ A i < 2 20 1 \leq n, m \leq 100000,0 \leq x<2^{20}, 1 \leq l_{i} \leq r_{i} \leq n, 0 \leq A_{i}<2^{20} 1≤n,m≤100000,0≤x<220,1≤li≤ri≤n,0≤Ai<220
// 思路:存下最近出现的数字的位置,查找与x的异或的数值是否在区间中#include <bits/stdc++.h>using namespace std;const int N=1e5 + 10;int dp[N]; //dp[i]表示从1到i区间内,存在a^b=x的最右边的b位置map<int,int> pos; //存放另一个数的位置int main() {ios_base::sync_with_stdio(0); cin.tie(0), cout.tie(0); int n, m, x; cin >> n >> m >> x; for(int i = 1; i <= n; i++) { int a; cin >> a; dp[i] = max(dp[i-1], pos[a^x]); //若i位置的数异或的数不存在则取上一个数异或得到x的 pos[a] = i; // } int l, r; while(m--) { cin >> l >> r; if(dp[r] >= l) puts("yes"); else puts("no"); } return 0;}X 图形 - DFS
问题描述
给定一个字母矩阵。一个 X 图形由中心点和由中心点向四个 45 度斜线方向引出的直线段组成,四条线段的长度相同,而且四条线段上的字母和中心点的字母相同。
一个 X 图形可以使用三个整数 r, c, L 来描述,其中 r, c 表示中心点位于第 r 行第 cc 列,正整数 LL 表示引出的直线段的长度。 对于 1 到 L 之间的每个整数 ii,X 图形满足:第 r-i 行第 c-i 列与第 rr 行第 c 列相同,第 r−i 行第 c+i 列与第 r 行第 c 列相同,第 r+i 行第 c−i 列与第 r 行第 c 列相同,第 r+i 行第 c+i列与第 r行第 c 列相同。
例如,对于下面的字母矩阵中,所有的字母 LL 组成一个 X图形,中间的 5 个 L 也组成一个 X 图形。所有字母 Q 组成了一个 X 图形。
L A A A L A A L Q L Q A A A L Q A A A L Q L Q A L A A A L A LAAALA\\ ALQLQA\\ AALQAA\\ ALQLQA\\ LAAALA LAAALAALQLQAAALQAAALQLQALAAALA
给定一个字母矩阵,请求其中有多少个 XX 图形。
输入格式
输入第一行包含两个整数 n,m,分别表示字母矩阵的行数和列数。
接下来 n 行,每行 m 个大写字母,为给定的矩阵。
输出格式
输出一行,包含一个整数,表示答案。
样例输入
5 6LAAALAALQLQAAALQAAALQLQALAAALA样例输出
3评测用例规模与约定
对于 50% 的评测用例,1 <= n, m <= 10。
对于所有评测用例,1 <= n, m <= 100。
#include <iostream>#include <cstring>#include <algorithm>#include <cstdio>using namespace std;const int N = 110;char g[N][N];int n, m;int cnt = 0;//爆搜void check(int r, int c, int u){ if(r - u < 0 || r + u > n || c + u > m || c - u < 0) return; if(g[r][c] == g[r + u][c - u] && g[r][c] == g[r - u][c + u] && g[r][c] == g[r + u][c + u] && g[r][c] == g[r - u][c - u]) { cnt ++; check(r, c, u + 1); }}int main(){ cin >> n >> m; for(int i = 0; i < n; i ++) cin >> g[i]; for(int i = 0; i < n; i ++) for(int j = 0; j < m; j ++) { check(i, j, 1); } cout << cnt << endl; return 0;}时长计算 - 时分秒
问题描述
小蓝将自己的车停在路边,在同一天将车开走。给定停车时间和开走时间,请问小蓝停了多长时间?
输入格式
输入两行,第一行包含停车时间,第二行包含开走时间。
每个时间的格式为 HH:MM:SS,其中 HH 表示时,值为 0 到 23 的整数,如果小于 10 用 0 补齐两 位; MM 和 SS 分别表示分和秒,值为 0 到 59 的整数,小于 10 时用 0 补齐两位。
输出格式
输出总共停车的时间,格式为 HH:MM:SS。
样例输入
08:58:1017:20:31样例输出
08: 22: 21#include <iostream>using namespace std;int main(){ int a, b, c, h, m, s; scanf("%d:%d:%d", &a, &b, &c); //开始 scanf("%d:%d:%d", &h, &m, &s); //结束 if(s < c) s = s - c + 60, m --; //不够减借位 else s = s - c; if(m < b) m = m - b + 60, h --; //不够减借位 else m = m - b; h = h - a; printf("%02d:%02d:%02d\n", h, m, s); return 0;}回文日期
题目描述
2020 年春节期间,有一个特殊的日期引起了大家的注意:2020 年 2 月 2 日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202,恰好是一个回文数。我们称这样的日期是回文日期。
有人表示 20200202 是 “千年一遇” 的特殊日子。对此小明很不认同,因为不到 2 年之后就是下一个回文日期:20211202 即 2021 年 12 月 2 日。
也有人表示 20200202 并不仅仅是一个回文日期,还是一个 ABABBABA 型的回文日期。对此小明也不认同,因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期:21211212 即 2121 年 12 月 12 日。算不上 “千年一遇”,顶多算 “千年两遇”。
给定一个 8 位数的日期,请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。
输入描述
输入包含一个八位整数 N,表示日期。
对于所有评测用例, 10000101 ≤ N ≤ 89991231 10000101 \leq N \leq 89991231 10000101≤N≤89991231,保证 N 是一个合法日期的 8 位数表示。
输出描述
输出两行,每行 1 个八位数。第一行表示下一个回文日期,第二行表示下一个 ABABBABA 型的回文日期。
输入输出样例
示例
输入
20200202输出
2021120221211212#include<bits/stdc++.h> using namespace std;int D[13] = {0 , 31 , 28 , 31 , 30 , 31 , 30 , 31 , 31 , 30 , 31 , 30 , 31};bool is_leap(int y){ //闰年 return y % 400 == 0 || (y % 4 == 0 && y % 100 != 0);}bool ok(string s){ //检测回文 if(s[0] == s[2] && s[0] == s[5] && s[0] == s[7] && s[1] == s[3] && s[1] == s[4] && s[1] == s[6]) return true; return false;}signed main(){ string S , ans1 = "" , ans2 = ""; cin >> S; //ans1和ans2都不为空则结束 for(int i = stoi(S.substr(0 , 4)) ; ans1 == "" || ans2 == "" ; i ++){ string s = to_string(i) , t = to_string(i); reverse(t.begin() , t.end()); s += t; if(s <= S) continue ; //下一个回文日期 - ans为更大的 int y = stoi(s.substr(0 , 4)) , m = stoi(s.substr(4 , 2)) , d = stoi(s.substr(6 , 2)); if(is_leap(y)) D[2] = 29; else D[2] = 28; if(m < 1 || m > 12) continue ; if(d < 1 || d > D[m]) continue ; if(ans1 == "") ans1 = s; //ABABBABA if(ok(s) && ans2 == "") ans2 = s; //下一个回文日期 } cout << ans1 << endl << ans2 << endl; return 0;}#include <iostream>using namespace std;bool isLeap(int y){ return (y%4==0&&y%100!=0)||(y%400==0);}bool check(int year,int month,int day){//判断是否为合法日期 if(month>12||month==0) return false; if(day>31) return false; if(month==2){ if(isLeap(year)&&day>29) return false; if(!isLeap(year)&&day>28) return false; } if(month==4||month==6||month==9||month==11){ if(day>30) return false; } return true;}int main(){ int n,i; cin>>n; int a,b,c,d,e,f,g,h;//8位数字 int year,month,day; bool flag=false; for(i=n+1;i<=99999999;i++){ //暴力枚举 year=i/10000; month=(i%10000)/100; day=i%100; a=i%10; b=(i/10)%10; c=(i/100)%10; d=(i/1000)%10; e=(i/10000)%10; f=(i/100000)%10; g=(i/1000000)%10; h=(i/10000000)%10; if(a==h&&b==g&&c==f&&d==e&&flag==false){ if(check(year,month,day)){ cout<<i<<endl; flag=true;//只输出一个回文 } } if(a==h&&b==g&&c==f&&d==e&&a==c&&b==d){ if(check(year,month,day)){ cout<<i<<endl; break; } } } return 0;}付账问题 - 贪心
题目描述
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。
现在有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 a i a_i ai
元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?
为了公平起见,我们希望在总付钱量恰好为 S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 分钱的整数倍。你需要输出最小的标准差是多少。
标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的"偏差有多大"。形式化地说,设第 i 个人付的钱为 b i b_i bi元,那么标准差为 :
S = 1 n ∑ i = 1 n ( b i − 1 n ∑ i = 1 n b i ) 2 S=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(b_i-\frac{1}{n}\sum_{i=1}^{n}b_i)^{2}} S=n1∑i=1n(bi−n1∑i=1nbi)2
输入描述
第一行包含两个整数 n、S;
第二行包含 nn 个非负整数 a 1 , ⋯ , a n a_1, \cdots, a_n a1, ⋯, an
其中, n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 9 n \leq 5 \times 10^5, 0 \leq a_i \leq 10^9 n≤5×105,0≤ai≤109
输出描述
输出最小的标准差,四舍五入保留 4 位小数。
保证正确答案在加上或减去 1 0 − 9 10^{−9} 10−9
后不会导致四舍五入的结果发生变化。
输入输出样例
示例
输入
5 2333666 666 666 666 666
输出
0.0000【证明:用均值不等式】
若每个人a[i] > avg = s / n , 则每个人付s / n ==> 标准差 = 0
若有人仅有 a[i] < avg 不够均摊 ,则付a[i], 剩下a[i] - s / n 均摊给其他人
结论:从小到大枚举:能先判断其他人补差多少(补钱少的人不够需均摊的部分)
#include <bits/stdc++.h>using namespace std;const int N = 500010;int n;int a[N];int main(){ long double s; cin >> n >> s; for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]); sort(a, a + n); //从小到大排序后, 小的先付,若有差价不足均摊, 匀到后面大的支付剩下的部分的均摊值 long double res = 0, avg = s / n; for (int i = 0; i < n; i ++ ) { double cur = s / (n - i);//cur为当前均值:剩下的钱均摊给剩下的人 if (a[i] < cur) cur = a[i];//若钱不够帮助均摊, 则剩余的全付 res += (cur - avg) * (cur - avg); //计算平方和 : 方差 = 各个元素与均值的差的平方和 / 元素个数 s -= cur;//减去每个人的付款 ,剩下后面的人需均摊的部分 - 循环下一位 } printf("%.4Lf\n", sqrt(res / n));//标准差 = sqrt(方差) return 0;}?填空
蛇形填数 - 模拟
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
如下图所示,小明用从 11 开始的正整数“蛇形”填充无限大的矩阵。
1 2 6 7 15 ...3 5 8 14 ...4 9 13 ...10 12 ...11 ......容易看出矩阵第二行第二列中的数是 55。请你计算矩阵中第 2020 行第 2020 列的数是多少?
#include<bits/stdc++.h>using namespace std;int g[200][200];int row = 0, col = 0, cnt = 1; //行 列 数值int n = 20;/*void check(int n){ for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { cout << g[i][j] << " "; } puts(""); }}*/int main() { g[0][0] = 1; //[第一格] while(!g[n - 1][n - 1]) //【没有填完】 { //右移 g[row][++ col] = ++ cnt; if(!row) //在第一行-下一步向左下方,走到第一列 { while(col) g[++row][--col] = ++ cnt; //走到左下角再向下移动-再走到右上角 g[++row][col] = ++ cnt; while(row) g[--row][++col] = ++ cnt; } } // check(n); cout << g[n - 1][n - 1] << endl; return 0;}补充类似题[756. 蛇形矩阵]
输入两个整数 n 和 m,输出一个 n 行 m 列的矩阵,将数字 1 到 n×m 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 n 和 m。
输出格式
输出满足要求的矩阵。
矩阵占 n 行,每行包含 m 个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
3 3输出样例:
1 2 38 9 47 6 5向量枚举法
d与dx和dy初始值会影响输出结果!!!(方向顺序 : 顺时针)
#include<iostream>using namespace std;const int N = 110;int n,m;int q[N][N];int main(){ scanf("%d%d",&n,&m); int dx[] = {-1,0,1,0} , dy[] = {0,1,0,-1};//固定风格写:-1开始-1结束 int x = 0,y = 0,d = 1;// d用于方向选择 1, 2, 3, 0 【上右下左】 d与dx和dy初始值会影响输出结果!!! //DFS搜索 【注意方向向量必须先判断右到不能走再往下走,再判断左, 再判断上(即此题固定右下左上)】 for(int i = 1;i <= n * m;i++) //【用i赋值且遍历n*m格 】 { q[x][y] = i; //赋值:每轮填i int a = x + dx[d], b = y + dy[d]; if(a < 0 ||a >= n || b < 0 || b >= m || q[a][b]) //【出界或(a,b)已填过不能走,判断下一个方向】 { d = (d+1) % 4;//判断下一个方向 【方向循环*妙*】 a = x + dx[d], b = y + dy[d]; } x = a ,y = b; // 新起点 } for(int i = 0;i < n;i++) { for(int j = 0;j < m;j++) { printf("%d ",q[i][j]); } puts(""); } return 0;}棋盘放麦子
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
你一定听说过这个故事。国王对发明国际象棋的大臣很佩服,问他要什么报酬,大臣说:请在第 1 个棋盘格放 1 粒麦子,在第 2 个棋盘格放 2 粒麦子,在第 3 个棋盘格放 4 粒麦子,在第 4 个棋盘格放 8 粒麦子,…后一格的数字是前一格的两倍,直到放完所有棋盘格(国际象棋共有 64 格)。
国王以为他只是想要一袋麦子而已,哈哈大笑。
当时的条件下无法准确计算,但估算结果令人吃惊:即使全世界都铺满麦子也不够用!
请你借助计算机准确地计算,到底需要多少粒麦子。
答案显然是: 2 64 − 1 ( 可以用等比数列运算 ) 答案显然是:2^{64}-1~~(可以用等比数列运算)~~~ 答案显然是:264−1 (可以用等比数列运算) (long long的边界值)
#include <iostream>using namespace std;#define ans 0xFFFFFFFFFFFFFFFFtypedef unsigned long long ULL;ULL qmi(ULL a, ULL k){ ULL res = 1; while(k) { if(k & 1) res = res * a; a = a * a; k >>= 1; } return res;}int main(){ cout<<qmi(2, 64) - 1<<endl; //或者0xFFFFFFFFFFFFFFFF return 0;}质数 - 线性筛法
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
我们知道第一个质数是 2、第二个质数是 3、第三个质数是 5……
请你计算第 2019 个质数是多少?
#include <iostream>using namespace std;typedef long long LL;const int N = 2100, M = 1e6 + 10;int primes[N];bool st[M];int cnt;void get_primes(int n){ for(int i = 2; i <= n; i++) { if(!st[i]) primes[cnt ++] = i; for(int j = 0; primes[j] <= n / i; j++) //筛去质数的倍数 { st[primes[j] * i] = true; if(i % primes[j] == 0) break; } }}int main(){ int n = M; get_primes(n); printf("%d\n", primes[2018]); // printf("17569"); return 0;}猜生日
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
今年的植树节(2012 年 3月 12 日),小明和他的叔叔还有小伙伴们一起去植树。休息的时候,小明的同学问他叔叔多大年纪,他叔叔说:“我说个题目,看你们谁先猜出来!”
“把我出生的年月日连起来拼成一个 8 位数(月、日不足两位前补 0)正好可以被今天的年、月、日整除!”
他想了想,又补充到:“再给个提示,我是 6 月出生的。”
根据这些信息,请你帮小明算一下,他叔叔的出生年月日。
格式是年月日连成的 8 位数。例如,如果是 1948 年 6 月 12 日,就写:19480612。
#include <bits/stdc++.h>using namespace std;int main(){ string s = ""; int num = 0; for(int i = 1900; i <= 2012; i++) for(int j = 1; j <= 31; j++) { if(j < 10) s = to_string(i) + '0' + '6' + '0' + to_string(j); else s = to_string(i) + '0' + '6' + to_string(j); num = stoi(s); // cout << num << endl; if(num % 2012 == 0 && num % 3 == 0 && num % 12 == 0) //可以被今天的年、月、日整除 2012 年 3 月 12 日 { printf("%d", num); break; } } return 0;}含 2 天数 - 日期模拟 - 国赛
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴,因为每天日历上都可以看到 2。
如果日历中只显示年月日,请问从公元 1900 年 1 月 1 日到公元 9999年 12 月 31 日,一共有多少天日历上包含 2。即有多少天中年月日的数位中包含数字 2。
写法一:
#include <iostream>using namespace std;typedef long long LL;int mm[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};LL ans = 0;//闰年含2天数多一天(2月29日 含2)bool is_leap(int y){ return y % 400 == 0 || y % 4 == 0 && y % 100 != 0;;}bool is_2(int m, int d) { while(m) { if(m % 10 == 2) return true; m /= 10; } while(d) { if(d % 10 == 2) return true; d /= 10; } return false;}int get() //年没有2时月和天中含2天数-平年 179 - 正确!!!{ int res = 0; for(int i = 1; i <= 12; i++) for(int j = 1; j <= mm[i];j ++) if(is_2(i, j)) res ++; return res;}bool check_y(int y){ while(y) { if(y % 10 == 2) return true; y /= 10; } return false;}int main() //日历中只显示年月日{ int t = get(); //不用重复循环 for(int i = 1900; i <= 9999; i++) //年 { //年是否有2 + 是否为闰年 if(check_y(i)) ans += 365 + is_leap(i); else ans += t + is_leap(i); } printf("%lld\n", ans); return 0;}写法二:(填空无时间限制)
#include <iostream>using namespace std;int days[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};bool is_leap(int year){return year % 400 == 0 || year % 4 == 0 && year % 100 != 0;}bool check1(int x) //日期是否合法{int year = x / 10000;int month = x / 100 % 100;int day = x % 100;if(month < 1 || month > 12) return false;if(month != 2) {if(day < 1 || day > days[month]) return false;}else{if(day < 1 || day > days[month] + is_leap(year)) return false;}return true;}bool check2(int x){while(x){if(x % 10 == 2) return true;x /= 10;}return false;}int main(){int ans = 0;for (int i = 19000101; i <= 99991231; i ++) //枚举年月日if(check1(i) && check2(i)) ans ++;cout << ans << endl;return 0;}填算式 - 国赛
问题描述
请看下面的算式:
(ABCD - EFGH) * XY = 900
每个字母代表一个 0 ~ 9 的数字,不同字母代表不同数字,首位不能为 0。
比如,(5012 - 4987) * 36 就是一个解。
请找到另一个解,并提交该解中 ABCD 所代表的整数。
答案提交
请严格按照格式,通过浏览器提交答案。
注意:只提交 ABCD 所代表的整数,不要写其它附加内容,比如:说明性的文字。
#include <bit/stdc++.h>using namespace std;int s[10];int main(){for (int i = 0; i < 10; i ++) s[i] = i;do{if(s[0] != 0 && s[4] != 0 && s[8] != 0){int a = s[0] * 1000 + s[1] * 100 + s[2] * 10 + s[3];int b = s[4] * 1000 + s[5] * 100 + s[6] * 10 + s[7];int c = s[8] * 10 + s[9];if((a - b) * c == 900) cout << a << endl; //6048}}while(next_permutation(s, s + 10));return 0;}国王的遗产
【问题描述】
X国是个小国。国王K有6个儿子。在临终前,K国王立下遗嘱:国王的一批牛作为遗产要分给他的6个儿子。
其中,大儿子分1/4,二儿子1/5,三儿子1/6,… 直到小儿子分1/9。牛是活的,不能把一头牛切开分。
最后还剩下11头牛,分给管家。
请计算国王这批遗产中一共有多少头牛。
#include <iostream>using namespace std;int main(){double x = 1 - 1.0 / 4 - 1.0 / 5 - 1.0 / 6 - 1.0 / 7 - 1.0 / 8 - 1.0 / 9;cout << 11 / x << endl; //2520return 0;} 填空题边界判断:如果不断提高循环次数,答案还是不变,则99%是正确
除法相等可以等式相乘变成判断乘法相等
本质上升序列
问题描述
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列,类似的单调递增子序列还有 lnq、i、ano。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,
例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao,小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。
它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分两行显示):
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl本质不同的递增子序列有多少个?
#include <bits/stdc++.h> //没有重复出现的上升子序列 - 本质上升子序列using namespace std;const int N = 210;int f[N];int main(){ // f[i]:以字符 s[i] 结尾的本质不同递增子序列的数量 string s = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl"; for (int i = 0; i < s.size(); i++) f[i] = 1; //自身长度1 for (int i = 0; i < s.size(); i++) { for (int j = 0; j < i; j++) { if (s[i] > s[j]) f[i] += f[j]; //类比LIS - 以i结尾方案数 += j结尾方案数 if (s[i] == s[j]) f[i] = 0; //前后出现相等字符 - 不是本质子序列 - 方案数取0 } } int ans = 0; for (int i = 0; i <s.size(); i++) ans += f[i]; cout << ans << endl; return 0;}天干地支 - 国赛
题目描述
古代中国使用天干地支来记录当前的年份。
天干一共有十个,分别为:甲(jiǎ)、乙(yǐ)、丙(bǐng)、丁(dīng)、戊(wù)、己(jǐ)、庚(gēng)、辛(xīn)、壬(rén)、癸(guǐ)。
地支一共有十二个,分别为:子(zǐ)、丑(chǒu)、寅(yín)、卯(mǎo)、辰(chén)、巳(sì)、午(wǔ)、未(wèi)、申(shēn)、酉(yǒu)、戌(xū)、 亥(hài)。
将天干和地支连起来,就组成了一个天干地支的年份,例如:甲子。
2020 年是庚子年。
每过一年,天干和地支都会移动到下一个。例如 2021 年是辛丑年。
每过 60 年,天干会循环 6 轮,地支会循环 5 轮,所以天干地支纪年每 6060 年轮回一次。例如 1900 年,1960 年,2020 年都是庚子年。
给定一个公元纪年的年份,请输出这一年的天干地支年份。
输入描述
输入一行包含一个正整数,表示公元年份。
其中有 ,输入的公元年份为不超过 9999 的正整数。
输出描述
输入一行包含一个正整数,表示公元年份。
输入输出样例
示例
输入
2020输出
gengzi#include <iostream>using namespace std;string a[10] = {"geng", "xin", "ren", "gui", "jia", "yi" , "bing", "ding", "wu", "ji"};string b[12] = {"shen", "you", "xu", "hai", "zi", "chou", "yin", "mou", "chen", "si", "wu", "wei"};int main(){ int year; cin >> year; cout << a[year % 10] << b[year % 12] << endl; return 0;}卡片 - 统计
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝有很多数字卡片,每张卡片上都是数字 0 到 9。
小蓝准备用这些卡片来拼一些数,他想从 1 开始拼出正整数,每拼一个,就保存起来,卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。
例如,当小蓝有 30 张卡片,其中 0 到 9 各 3 张,则小蓝可以拼出 1 到 10,
但是拼 11 时卡片 1 已经只有一张了,不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张,共 2021 张,请问小蓝可以从 1 拼到多少?
提示:建议使用计算机编程解决问题。
运行限制
最大运行时间:1s
最大运行内存: 128M
#include <iostream>using namespace std;int cnt[11];bool calc(int x){ while(x) { if(++ cnt[x % 10] > 2021) return false; x /= 10; } return true;}int main(){ int x = 1; while(true) { if(!calc(x)) break; x ++; } x --; //最后一次不行 !!! ans = x - 1 cout << x << endl;; return 0;}跑步锻炼 - 日期
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝每天都锻炼身体。
正常情况下,小蓝每天跑 1 千米。如果某天是周一或者月初(1 日),为了激励自己,小蓝要跑 2 千米。如果同时是周一或月初,小蓝也是跑 2 千米。
小蓝跑步已经坚持了很长时间,从 2000 年 1 月 1 日周六(含)到 2020年 10 月 1 日周四(含)。请问这段时间小蓝总共跑步多少千米?
答案:8879
#include <iostream>using namespace std;bool is_leap(int y){ //闰年判断 return y % 400 == 0 || (y % 4 == 0 && y % 100 != 0);}int mm[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};bool check(int i){ // 合法日期 int y= i / 10000, m = i % 10000 / 100, d = i % 100; if(m <= 0 || m > 12 || d <= 0) return false; if(m != 2 && d > mm[m]) return false; else //2月是否闰年 { if(d > mm[m] + is_leap(y)) return false; } return true;}int main(){ int ans = 0,cnt = 0; for(int i = 20000101;i <= 20201001; i++) { int d = i % 100; if(check(i)) //合法日期 天数++,星期++ { cnt++; ans++; // 无论是星期一或是每个月第一天,先跑1km if(cnt % 7 == 3 || d == 1) // 【cnt第一天是星期六,cnt % 7 == 3时为星期一】 ans++; //如果是星期一或者是每个月第一天或者同时是星期一和每个月第一天,那就在1km基础上再跑1km } } cout << ans << endl;; return 0;}最大子矩阵
问题描述
下面是一个 20 × 20 20\times 20 20×20 的矩阵,矩阵中的每个数字是一个 1 到 9 之间的数字,请注意显示时去除了分隔符号。
6985924183938786894117615876963131759284373473483266274834855367125655616786474316121686927432329479135474133499627734472797994592984882468753776983346838791379564934213653657177452192437929387261138293919353216243561277542961447639692577889623397251379473293381443494533129939975611718829888775934996121686889572134852255485345959294726896321249633182425549221359364719193427269656436895944919899246矩阵中一个子矩阵的值是指子矩阵中所有数值的和。
请问,矩阵中值最大的一个 5 × 5 5\times 5 5×5 的子矩阵的值是多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:154
#include<bits/stdc++.h>using namespace std;string strs[] = { "69859241839387868941", "17615876963131759284", "37347348326627483485", "53671256556167864743", "16121686927432329479", "13547413349962773447", "27979945929848824687", "53776983346838791379", "56493421365365717745", "21924379293872611382", "93919353216243561277", "54296144763969257788", "96233972513794732933", "81443494533129939975", "61171882988877593499", "61216868895721348522", "55485345959294726896", "32124963318242554922", "13593647191934272696", "56436895944919899246" };int main(){ int ans = 0; for(int i = 0;i <= 15; i++){ for(int j = 0;j <= 15; j++){ int sum = 0; for(int k = i; k < i + 5; k++){ for(int h = j;h < j + 5; h++){ sum += (strs[k][h] - '0'); } } ans = max(ans, sum); } } cout << ans << endl; //154}#include<bits/stdc++.h>using namespace std;int s[25][25];int main(){ int n = 20; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) { scanf("%1d",&s[i][j]); //只读入1 int [不会读入时建议写数组] s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; } int res = 0; for(int i = 5; i <= n; i++) { for(int j = 5; j <= n; j++) //s[1][1] ~ s[5][5] 开始 s[5][5] - s[0][5] - s[5][0] + s[0][0] { int x1 = i - 4, y1 = j - 4, x2 = i, y2 = j; int sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]; res = max(res, sum); } } // cout << res << endl; cout << 154 << endl;}最小公倍数
问题描述
如果一个整数 M 同时是整数 AA 和 B 的倍数,则称 M 是 A 和 B 的公倍数,公倍数中最小的一个正 整数称为最小公倍数。
例如 : 2021 和 86 的最小公倍数是 4042.
请问在 1 (含) 到 2021 (含) 中,有多少个数与 2021 的最小公倍数是 4042 。
答案提交
这是一道结果填空的题 ,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:3
#include <bits/stdc++.h>using namespace std;int lcd(int a, int b){ return a * b / __gcd(a, b);}int main(){ int ans = 0; for(int i = 1; i <= 2021; i++) if(lcd(i, 2021) == 4042) ans ++; cout << ans << endl; //3 return 0;}平方和拆分
问题描述
10 是一个非常特殊的数,它可以表示成两个非负整数的平方和, 10 = 3 ∗ 3 + 1 ∗ 1 10=3 * 3+1 * 1 10=3∗3+1∗1 。 9 也是同样特殊的数,它可以表示成 9 = 3 ∗ 3 + 0 ∗ 0 9=3 * 3+0 * 0 9=3∗3+0∗0。 请问,在 1 到 2021 中有多少个这样的数?
请注意,有的数有多种表示方法,例如 25 = 5 ∗ 5 + 0 ∗ 0 = 3 ∗ 3 + 4 ∗ 4 25=5 * 5+0 * 0=3∗3+4 *4 25=5∗5+0∗0=3∗3+4∗4,在算答案时只算一次。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只 填写这个整数,填写多余的内容将无法得分。
答案:624
#include <iostream>using namespace std;int f[55]; //打表bool check(int x){ // for(int i = 1; i <= 50; i++) if(i * i == x) return true; //自己为平方数 for(int i = 0; i <= 50; i++) for(int j = 0; j <= 50; j++) if(x == f[i] + f[j]) return true; return false;}int main(){ for(int i = 1; i <= 50; i++) f[i] = i * i; int ans = 0; for(int i = 1; i <= 2021; i++) if(check(i)) ans ++; cout << ans << endl; return 0;}#include <iostream>#include <bitset>using namespace std;// bitset <2050> st;bool st[2050];int main () { for (int i = 0; i <= 50; i++) for (int j = 0; j <= 50; j++) st[i * i + j * j] = 1; int ans = 0; for (int i = 1; i <= 2021; i++) if (st[i]) ans ++; cout << ans << endl; return 0;}平方和
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明对数位中含有 2、0、1、9 的数字很感兴趣,在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40 ,共 28 个,他们的和是 574 ,平方和是 14362 。
注意,平方和是指将每个数分别平方后求和。
请问,在 1 到 2019 中,所有这样的数的平方和是多少?
答案:2658417853
#include <bits/stdc++.h>using namespace std;bool judge(int x){ while(x) { if(x % 10 == 2 || x % 10 == 0 || x % 10 == 1 || x % 10 == 9) return true; x /= 10; } return false;}int main(){ long long sum = 0; for(int i = 1; i <= 2019; i++) { if(judge(i)) sum += i * i; } cout << sum; return 0;}string类函数
#include <bits/stdc++.h>using namespace std;int main(){ long long sum = 0; for(int i = 1; i <= 2019; i++) { string s = to_string(i); if(~s.find('2') || ~s.find('0') || ~s.find('1') || ~s.find('9')) //【没有找到返回-1】 sum += i * i; } cout << sum; return 0;}分数
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
1 1 + 1 2 + 1 4 + 1 8 + ⋯ \frac{1}{1} + \frac{1}{2} + \frac{1}{4} + \frac{1}{8}+\cdots 11+21+41+81+⋯
每项是前一项的一半,如果一共有 20 项,求这个和是多少,结果用分数表示出来。
类似: 3 2 \frac{3}{2} 23 ,当然,这只是加了前 2 项而已。分子分母要求互质。
答案:1048575/524288
#include <bits/stdc++.h>using namespace std;int main(){ int a = pow(2,20) - 1; int b = pow(2,19); printf("%d/%d", a , b); return 0;}