【综合评价分析】topsis评价 原理+完整MATLAB代码+详细注释+操作实列

文章目录

1、TOPSIS法的原理

2、TOPSIS法案例分析

3.建立模型并求解

3.1数据预处理

3.2代码实现数据预处理

3.3 本案例中数据预处理的运用

4.计算距离和评价指标

4.1 代码

4.2 运行结果

5.总结

---

1、TOPSIS法的原理

       设多属性决策方案（单元）为D={d1,d2,…,dm}，衡量方案优劣的属性变量为x1,x2,…,xn,这些方案D中的每个方案di(i=1,2,…）的n个属性构成向量[ai1,ai2,…,ain]，将其作为n维空间的一个点，能唯一地代表方案di。

       正理想解C*是一个方案D中不存在的虚拟最佳方案，它的每个属性都是决策矩阵中该属性的最优值；而负理想解C0则是虚拟的最差方案，它的每个属性都是决策矩阵中该属性的最差值。

       评价与决策原理：将D中每个备选方案di与正理想解C*和负理想解C0的距离进行比较，既靠近C*，又远离C0的方案是D中最优方案，并且可以据此排定D中各个备选方案的优先序。

       原理中距离的选取不同，也会影响排序和评价，TOPSIS法常用的是欧几里得距离。

2、TOPSIS法案例分析

       为了客观评价我国研究生教育的实际状况和各研究生院的教学质量，国务院学位办组织过一此研究生院的评估。为了取得经验，先选了5所研究生院，收集有关数据进行了式评估，表1给出了部分数据。

i院\指标j	人均专著x1(本/人）	生师比x2	科研经费x3（万元/年）	逾期毕业率x4（%）
1	0.1	5	5000	4.7
2	0.2	6	6000	5.6
3	0.4	7	7000	2.3
4	0.9	10	10000	2.3
5	1.2	2	400	1.8

符  号	说      明
i	研究院标号；i=1,2,3,4,5;
j	评价指标标号，j=1,2,3,4；
aij	第i研究院的第j指标的数据；
bij	aij的规范化后的数据;
cij	加权规范数据;
wj	第j指标的权重,j=1,2,3,4;
cj*	正理想解的第j指标；
cj0	负理想解的第j指标；
si*	第i研究院与正理想解的距离；
si0	第i研究院与负理想解的距离；
fi*	第i研究院的排序指标

3.建立模型并求解

3.1数据预处理

       属性值具有多种类型，包括效益型，即越大越好；成本型，即越小越好；区间型，即属性值落在某个区间最佳。

       数据规范化的必要性： （1）属性的上述不同类型值放在同一个表中（矩阵）中不便处理，即不变直接从数值大小区分优劣；（2）非量纲化，多属性评估与决策的难点就是属性值的不可公度性，即每一列都有不同计量单位，需要排除量纲的选用对决策和评估的影响；（3）归一化，属性值表中不同指标的属性值数值大小差别比较大（可能是科学计数法造成），为了直观，更为了便于采用各种多属性决策与评估进行评价，需要把属性表中不同属性数值归一化，即把表中数据都处理到[0,1]区间上。

效益型数据处理（即越大越好）规范化公式（也归一化）

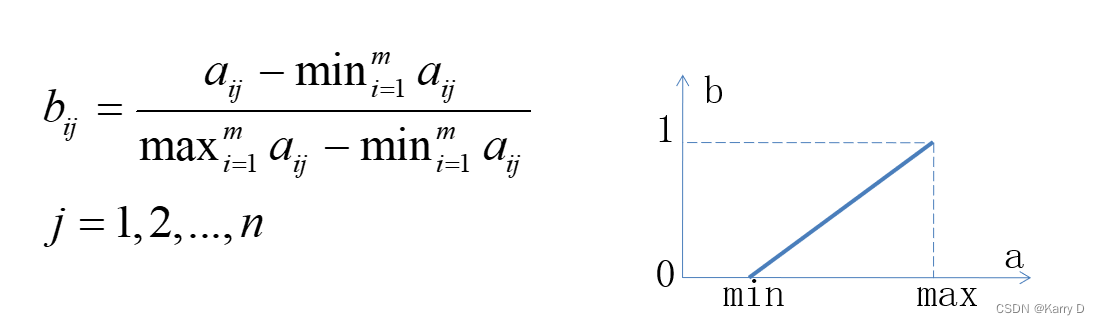
成本型数据处理（即数据越小越好）规范化公式

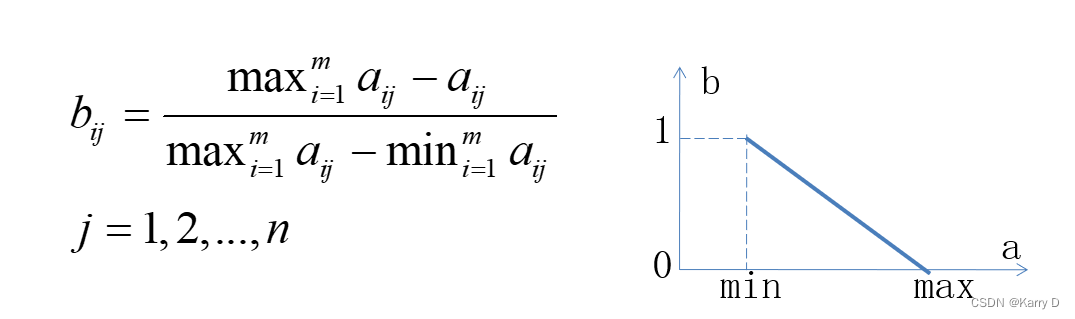
区间型数据处理公式

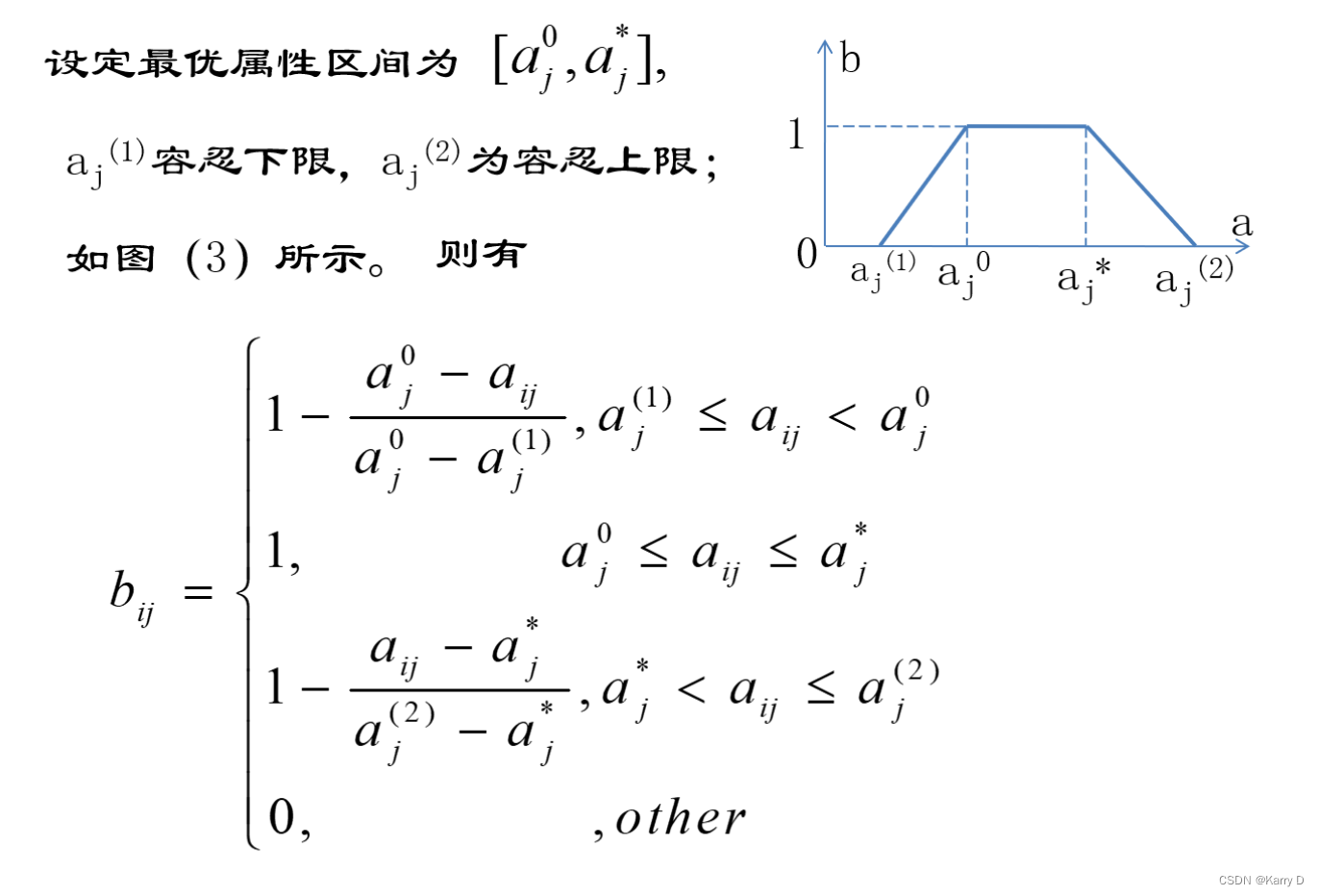
3.2代码实现数据预处理

%数据预处理方法：线性归一化%a为处理数据矩阵 u为选择处理方法 1为效益型 2为成本型 3为区间型 qujian为效益形中的最优属性区间 rennai为忍耐上下限区间function b=topsis(a,u,qujian,rennai)am1=min(a);am2=max(a);% 效益型数据处理（即数据越大越好）if u==1    b=(a-am1)./(am2-am1);% 成本型数据处理（即数据越小越好）elseif u==2    b=(am2-a)./(am2-am1);% 区间型数据处理elseif u==3    n=length(a);    for k=1:n        if a(k)>=rennai(1)&a(k)<qujian(1)            b(k)=1-(qujian(1)-a(k))/(qujian(1)-rennai(1));        elseif a(k)>=qujian(1)&a(k)<=qujian(2)            b(k)=1;        elseif a(k)>qujian(2)&a(k)<=rennai(2)            b(k)=1-(a(k)-qujian(2))/(rennai(2)-qujian(2));        else            b(k)=0;        end    endend

3.3 本案例中数据预处理的运用

       本案中，人均专著就是效益型指标；科研经费是成本型指标；逾期毕业率是效益型指标；而生师比是区间型指标，因为生师比太大，一个老师所带研究生太多，就越糟；生师比越小也越浪费教师资源，情况也越糟。设最优区间为[5,6]。逾期毕业率为成本型指标。

A=[0.1 0.2 0.4 0.9 1.2;   5 6 7 10 2;   5000 6000 7000 10000 400;   4.7 5.6 6.7 2.3 1.8];A=A';a1=A(:,1);a2=A(:,2);a3=A(:,3);a4=A(:,4);b1=topsis(a1,1);b2=topsis(a2,3,[5,6],[2,12]);b3=topsis(a3,2);b4=topsis(a4,2);[b1,b2',b3,b4]

运行结果：

 

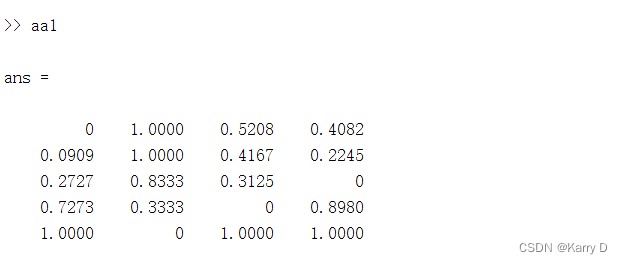
i院\指标j	人均专著x1(本/人）	生师比x2	科研经费x3（万元/年）	逾期毕业率x4（%）
1	0	1	0.5208	0.4082
2	0.0909	1	0.4167	0.2245
3	0.2727	0.8333	0.3125	0
4	0.7273	0.3333	0	0.8980
5	1	0	1	1

4.计算距离和评价指标

4.1 代码

A=[0.1 0.2 0.4 0.9 1.2;   5 6 7 10 2;   5000 6000 7000 10000 400;   4.7 5.6 6.7 2.3 1.8];A=A';a1=A(:,1);a2=A(:,2);a3=A(:,3);a4=A(:,4);b1=topsis1(a1,1);b2=topsis1(a2,3,[5,6],[2,12]);b3=topsis1(a3,2);b4=topsis1(a4,2);I=[1 1/3 2 3;3 1 4 2;1/2 1/4 1 2;1/3 1/2 1/2 1];[x,y]=eig(I);w1=x(:,1);w=w1/sum(w1);c1=b1*w(1);c2=b2'*w(2);c3=b3*w(3);c4=b4*w(4);C=[c1,c2,c3,c4];cx=[0.2494 0.4814 0.1482 0];cL=[0 0 0 0.1210];for k=1:5    s1(k)=dist(C(k,:),cx');    s2(k)=dist(C(k,:),cL');endf=s2./(s1+s2);[s1',s2',f']

4.2 运行结果

研究院	正理想解距离S*	负理想解距离s0	综合指标f
1	0.2640	0.4929	0.6512
2	0.2442	0.4949	0.6696
3	0.2230	0.4270	0.6570
4	0.3760	0.2425	0.3920
5	0.4964	0.2901	0.3688

5.总结

    根据表5，5个研究院综合评价的优劣顺序为 2 3 1 4 5.