给定一个 N×M 的矩阵 A,请你统计有多少个子矩阵 (最小 1×1,最大 N×M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式
第一行包含三个整数 N,M 和 K。
之后 N 行每行包含 M 个整数,代表矩阵 A。
输出格式
一个整数代表答案。
数据范围
对于 30% 的数据,N,M≤20,
对于 70% 的数据,N,M≤100,
对于 100% 的数据,1≤N,M≤500;0≤Aij≤1000;1≤K≤250000000。
输入样例:
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
输出样例:
19
样例解释
满足条件的子矩阵一共有 19,包含:
大小为 1×1 的有 10 个。
大小为 1×2 的有 3 个。
大小为 1×3 的有 2 个。
大小为 1×4 的有 1 个。
大小为 2×1 的有 3 个。
分析
此题就是二维前缀和 和 双指针,公式模板如下,可以画个方格图,每个方格就是一个点,就更清晰:
S[i, j] = 第i行j列格子左上部分所有元素的和 :a[i][j]=a[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]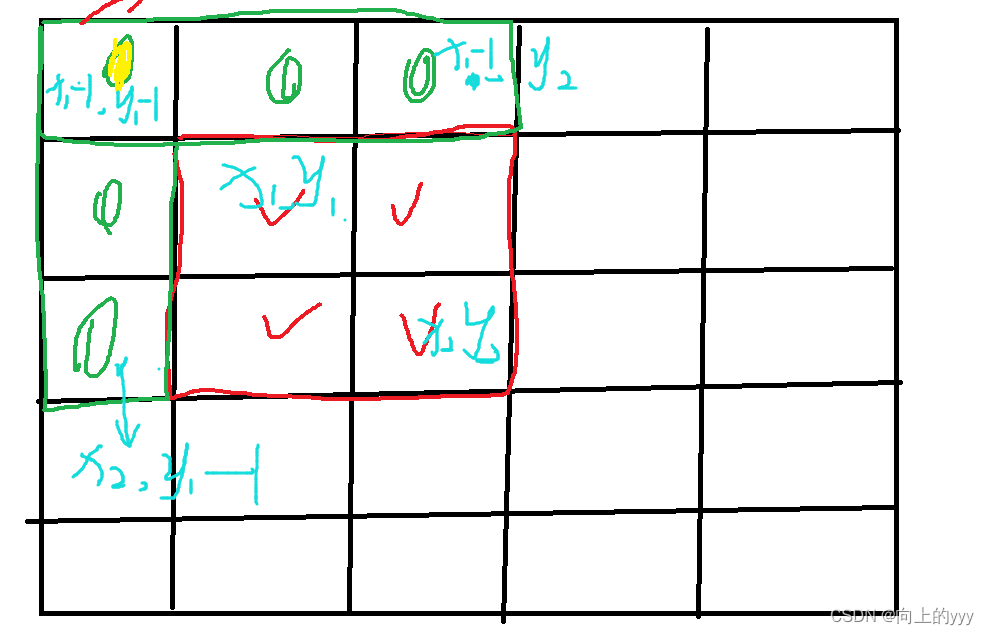
四层for暴力解法 O(N4)(70分)
枚举每个点为起点,和枚举每个点为终点,这样就可以得到所有的子矩阵(不重不漏),但时间复杂度是O(n^4),会超时;
#include <bits/stdc++.h>using namespace std;int n, m, k;int a[505][505];long long ans = 0;int main() { cin >> n >> m >> k; for (int i = 1; i <= n; ++i) { for (int j = 1; j <= m; ++j) { cin >> a[i][j]; //二维前缀和,第i行j列格子左上部分所有元素的和 a[i][j] = a[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]; } } for (int i = 1; i <= n; ++i) { for (int j = 1; j <= m; ++j) { for (int l = i; l <= n; ++l) { for (int p = j; p <= m; ++p) { //以(i, j)为左上角,(l, p)为右下角的子矩阵的和为: int sum = a[l][p] - a[l][j - 1] - a[i - 1][p] + a[i - 1][j - 1]; if (sum <= k) ans++; } } } } cout << ans; return 0;}双指针优化 O(N3)
i,j分别表示一个区域的左右边界,p,q来表示上下两个指针,p一开始在最上面,不断向下来找q,至到权值和小于等于k(而且不能越界也就是p>q),然后p q这片区域的行数q-p+1就是子矩阵的个数;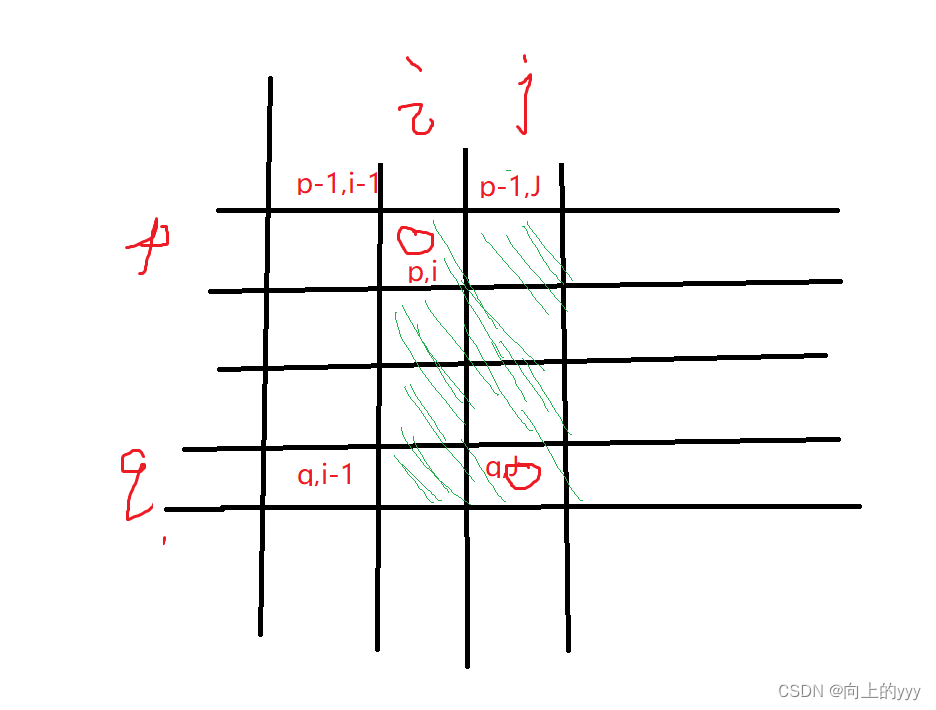
#include <bits/stdc++.h>using namespace std;int n, m, k;int a[505][505];long long ans = 0;int main() { //ios::sync_with_stdio(false); //cin >> n >> m >> k; scanf("%d%d%d", &n, &m, &k); for (int i = 1; i <= n; ++i) { for (int j = 1; j <= m; ++j) { scanf("%d", &a[i][j]); //二维前缀和,第i行j列格子左上部分所有元素的和 a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]; } } for (int i = 1; i <= m; ++i) { for (int j = i; j <= m; ++j) { for (int p = 1, q = 1; q <= n; ++q) { while (p <= q && a[q][j] - a[q][i - 1] - a[p - 1][j] + a[p - 1][i - 1] > k) { //一直让p指针下移到权值和<=k p++; } if (p <= q) { //在当前i,j的情况下,此时p q 之间的所有子矩阵都满足条件,一共q-p+1行 ans += (q - p + 1); } } } } cout << ans; return 0;}