全局池化
零、全局池化介绍一、全局平均池化二、全局最大池化
零、全局池化介绍
普通池化方法汇总详见:https://blog.csdn.net/qq_43665602/article/details/126625116
全局池化与普通池化的区别在于“局部区域”和“全局”:普通池化根据滑动窗口以及步长以逐步计算局部区域的方式进行;而全局池化是分别对每个通道的所有元素进行计算,谓之全局池化。
全局池化方式的优点:
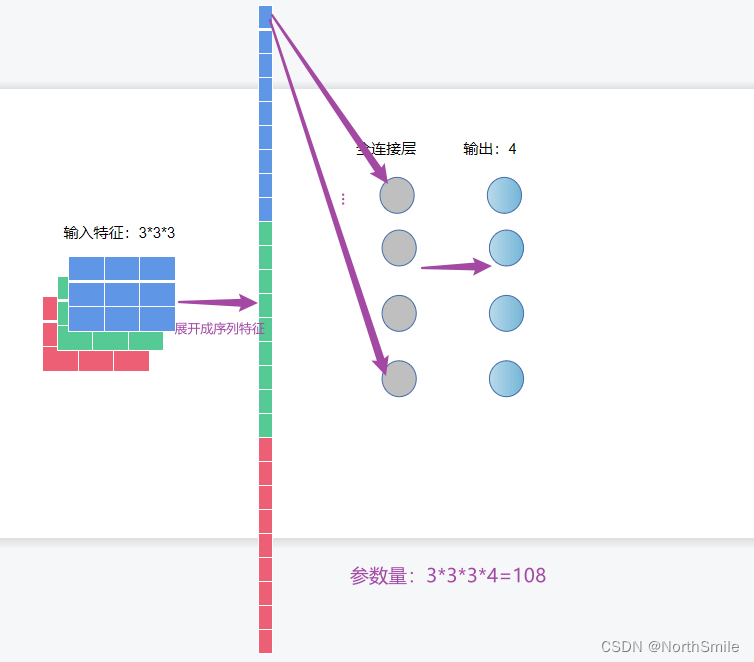
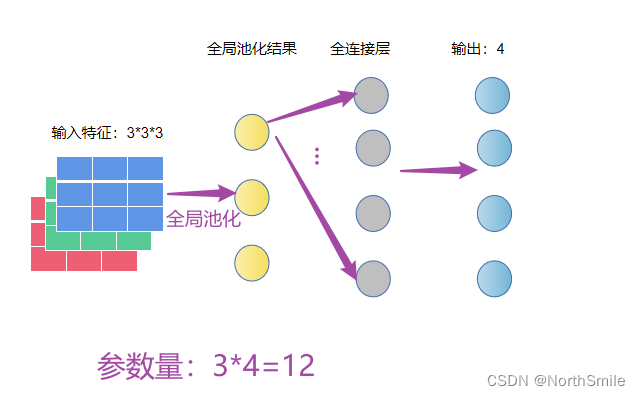
拿一个简单的网络验证参数量下降(此处只计算权重):
因为池化操作是沿着通道方向对该通道的特征进行,故对于输入(N,C,H,W),池化输出为(N,C)。此处输入特征为(N,C,H,W)=(1,3,3,3),故池化输出为(N,C)=(1,3)。
通过上面的简单介绍,想必对全局池化有了一个初步认识,接下来主要通过代码演示实际操作时如何进行。
Tensorflow对于普通池化和全局池化均有对应的实现方式,我们可以直接调用。但对于Pytorch我们发现nn下面只有普通池化,找不到全局池化的相关函数,但其实我们只需要将滑动窗口大小设置为特征图大小即可完成全局池化。对于二维池化,具体地设置参数kernel_size=(H_inp,W_inp),其中inp表示输入特征。
一、全局平均池化
全局平均池化是分别对每个通道进行平均运算,对该通道所有元素计算并输入一个平均值,故输出通道数不变,但每个通道只有一个元素。
inp=torch.tensor( [[[[8, 6, 1, 6, 4], [1, 0, 0, 4, 7], [7, 2, 7, 6, 1], [5, 5, 3, 9, 4], [6, 2, 9, 5, 9]], [[2, 2, 6, 5, 3], [4, 3, 1, 7, 6], [4, 0, 5, 6, 3], [8, 2, 1, 6, 8], [6, 6, 7, 6, 1]], [[3, 4, 8, 7, 9], [7, 2, 4, 9, 3], [1, 2, 7, 9, 1], [1, 8, 5, 0, 0], [1, 0, 5, 1, 6]]]])# torch.Size([1, 3, 5, 5])print(inp.shape)for c in range(3): print("c_{}".format(c),torch.sum(inp[0,c,:,:])/(inp.shape[2]*inp.shape[3]))print('-'*25)out=nn.AvgPool2d(kernel_size=(inp.shape[2],inp.shape[3]))(inp)print(out)print(out.shape)torch.Size([1, 3, 5, 5])# 手动计算每个通道的平均值c_0 tensor(4.6800)c_1 tensor(4.3200)c_2 tensor(4.1200)-------------------------# 全局平均池化结果:因为平均运算采取向下取整,故与手动计算的存在一点区别tensor([[[[4]], [[4]], [[4]]]])torch.Size([1, 3, 1, 1])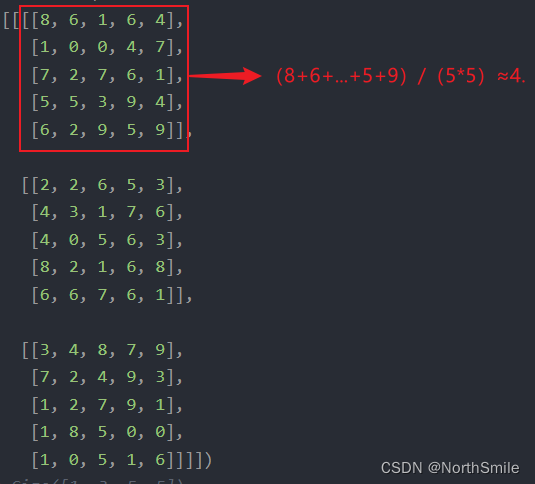
二、全局最大池化
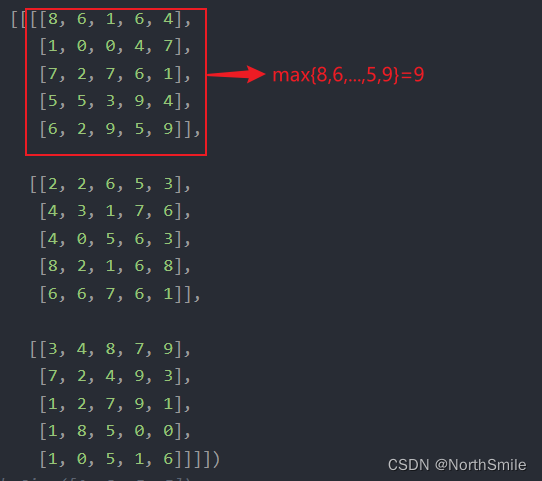
全局最大池化是分别对每个通道进行取最大值运算,对该通道所有元素取最大值,故输出通道数不变,但每个通道只有一个元素。
inp=torch.tensor([[[[8, 6, 1, 6, 4], [1, 0, 0, 4, 7], [7, 2, 7, 6, 1], [5, 5, 3, 9, 4], [6, 2, 9, 5, 9]], [[2, 2, 6, 5, 3], [4, 3, 1, 7, 6], [4, 0, 5, 6, 3], [8, 2, 1, 6, 8], [6, 6, 7, 6, 1]], [[3, 4, 8, 7, 9], [7, 2, 4, 9, 3], [1, 2, 7, 9, 1], [1, 8, 5, 0, 0], [1, 0, 5, 1, 6]]]],dtype=torch.float32)# torch.Size([1, 3, 5, 5])print(inp.shape)for c in range(3): print("c_{}".format(c),torch.max(inp[0,c,:,:]))print('-'*25)out=nn.MaxPool2d(kernel_size=(inp.shape[2],inp.shape[3]))(inp)print(out)print(out.shape)# 手动计算每个通道的最大值torch.Size([1, 3, 5, 5])c_0 tensor(9.)c_1 tensor(8.)c_2 tensor(9.)-------------------------# 全局最大化结果:分别对每个通道所有元素取最大值tensor([[[[9.]], [[8.]], [[9.]]]])torch.Size([1, 3, 1, 1])