提示:上一篇博客详解了A* 路径规划算法,这次学习Dijkstra算法
文章目录
一、Dijkstra应用背景二、Dijkstra算法原理及实现步骤1.算法的思路2.具体步骤 三、详细程序(Python)1.程序分步解析2.整体程序
提示:以下是本篇文章正文内容,下面案例可供参考
一、Dijkstra应用背景
Dijkstra是一种贪心算法,所谓贪心算法即始终保持当前的迭代解为当前最优解。它也是用来做路径规划问题,是单源最短路径问题的求解方法。
单源最短路径是指给定一个网络,指定一个起点A,终点G,求两点之间的最短路径。
如下图所示,每条路径都有一定的代价值,求从A到G的最小代价值的路线。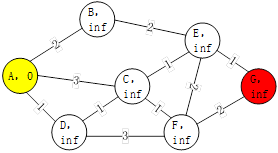
二、Dijkstra算法原理及实现步骤
1.算法的思路
起点为A点,终点为G点,B、C、D、E、F均为节点,每条线具备不同的代价值,例如B点距离A的代价值为2。每个节点除节点名之外,具备两个属性值:node_cost和parent。
node_cost记录当前节点到起点的已知节点的已知的最小总代价值,会随着规划路径不同而改变。
parent是指节点对应的父节点,例如E节点对应的父节点可以是B、C、F,由规划路径决定。
为了更好更清晰地分析此模型,用红色代表终点,天蓝色代表节点未完成遍历,橙色代表节点已经完成遍历,白色代表尚未纳入考虑范围。在算法开始之前,设定起点node_cost为0,其余节点node_cost设为无穷(inf),所有节点的parent设为空。
Dijkstra算法的核心是利用一次次的迭代过程找到一条node_cost最小的规划路径。从起点出发,计算其相邻的节点的node_cost,计算方式就是将起点的代价值与路径的代价相加,如果计算得到的node_cost值小于之前节点本身的node_cost值,就将其作为新的node_cost值,使其node_cost更小的节点成为其parent,并将节点表示为(节点名,node_cost值,parent),再将node_cost小的未遍历的节点作为新的起点,以此规律进行迭代。
2.具体步骤
第一次迭代过程起点A的相邻节点B、C、D的node_cost分别是2、3、1,父节点均是A点。所以,将B节点记录为(B,2,A),C节点与D节点同理。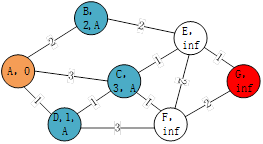 如图4-10,第二次迭代过程将D点作为起点,D的相邻节点有C、F,对于C节点的node_cost为2,因为小于之前为3的node_cost,所以其更新为(C,2,D),对于F节点node_cost为4。
如图4-10,第二次迭代过程将D点作为起点,D的相邻节点有C、F,对于C节点的node_cost为2,因为小于之前为3的node_cost,所以其更新为(C,2,D),对于F节点node_cost为4。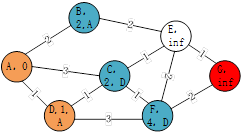 第三次迭代过程将B点作为起点,B节点的相邻节点E的node_cost为4,且B节点成为E节点的parent。
第三次迭代过程将B点作为起点,B节点的相邻节点E的node_cost为4,且B节点成为E节点的parent。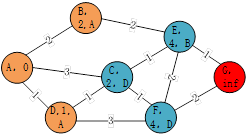 第四次迭代过程将C点作为起点,C的相邻节点E、F,对于C节点的node_cost都为3,并且对于E节点而言,3小于上次的值,所以更新node_cost和parent分别为3,C。
第四次迭代过程将C点作为起点,C的相邻节点E、F,对于C节点的node_cost都为3,并且对于E节点而言,3小于上次的值,所以更新node_cost和parent分别为3,C。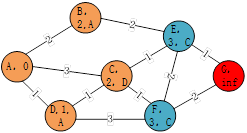 第五次迭代过程将E点作为起点,E的相邻节点即终点G,node_cost为4,就这样,通过迭代的过程从起点规划了一条通往终点的路径,再根据parent就能描绘出整条路径,如图4-13中红线所示。
第五次迭代过程将E点作为起点,E的相邻节点即终点G,node_cost为4,就这样,通过迭代的过程从起点规划了一条通往终点的路径,再根据parent就能描绘出整条路径,如图4-13中红线所示。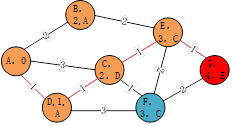
三、详细程序(Python)
1.程序分步解析
设置地图
构建上述的邻接矩阵
import numpy as np# ①构建地图mapping_list = [[np.inf for i in range(0, 7)] for i in range(0, 7)] # 构建全是无穷大的二维列表for i in range(0, 7): mapping_list[i][i] = 0 # 对角线处的值为0mapping_list[0][1] = 2mapping_list[0][2] = 3mapping_list[0][3] = 1mapping_list[1][4] = 2mapping_list[2][3] = 1mapping_list[2][4] = 1mapping_list[2][5] = 1mapping_list[3][5] = 3mapping_list[4][5] = 2mapping_list[5][6] = 2mapping_list[1][0] = 2mapping_list[2][0] = 3mapping_list[3][0] = 1mapping_list[3][2] = 1mapping_list[4][1] = 2mapping_list[4][2] = 1mapping_list[5][2] = 1mapping_list[5][3] = 3mapping_list[5][4] = 2mapping_list[6][5] = 2mapping_list = np.array(mapping_list) # 将mapping_list转换成数组形式print(mapping_list)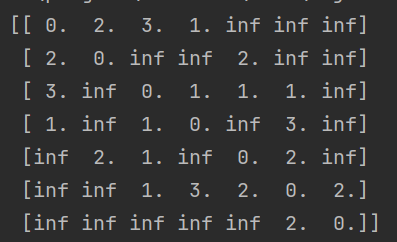
①计算A点所有相邻节点设置它们的node_cost(node_cost就是邻接矩阵中的值)以及父节点,并且将A点放入close_list里面
用0-1-2-3-4-5-6代表A-B-C-D-E-F-G节点
# ② 初始化node_cost = [[np.inf for i in range(0, 3)] for i in range(0, 7)] # 构建全是无穷大的二维列表# arr这个数组用来表示每个节点的[节点名 node_cost 父节点]for i in range(0, 7): node_cost[i][0] = i# 计算A点与它相邻的节点,更新其node_cost和父节点,并且将A点放入close_list里面node0 = 0close_list = []for i in range(0, 7): if mapping_list[int(node0)][i] < node_cost[i][1]: node_cost[i][2] = node0 node_cost[i][1] = mapping_list[int(node0)][i]close_list.append(int(node0))① 构建函数用来选择node_cost最小的节点,记作node0
# 1、构建函数用来选择node_cost最小的节点# 选择node_cost值最小的节点->node 0def choose_min(node_cost, close_list): node_cost = np.array(node_cost) # 将node_cost从list转换成array open_list = list(set(node_cost[:, 0].tolist()) - set(close_list)) # 建立一个open_list放入没有被遍历的点 final_list = [] for i in open_list: final_list.append(node_cost[int(i)].tolist()) final_list = np.array(final_list) # final_list转换成array,才可以利用np.where找最小值 node0 = final_list[np.where(final_list[:, 1] == final_list[:, 1].min())][0][0] # 将node_cost最小的点的节点名给node0 return int(node0)②构建count_cost函数用来计算相邻节点的node_cost
# 2、构建count_cost函数用来计算相邻节点的node_cost# 计算node0邻节点的node_cost,此时的node_cost值就是地图上的代价值加上父节点的代价值,如果已经比原来小则更新node_cost和父节点# 并将node0放入close_list里面def count_cost(mapping_list, node_cost, close_list): for i in range(0, 7): if mapping_list[node0][i] + node_cost[node0][1] < node_cost[i][1]: node_cost[i][2] = node0 node_cost[i][1] = mapping_list[node0][i] + node_cost[node0][1] close_list.append(node0) return [node_cost, close_list]迭代结束的条件是终点在close_list里面
# ④ 开始迭代----->迭代中止的条件:终点在close_list里面while 6 not in close_list: node0 = choose_min(node_cost, close_list) # 找node_cost最小的节点 [node_cost, close_list] = count_cost(mapping_list, node_cost, close_list) # 计算邻节点 # print(close_list)xn = 6x0 = 0destination_list = [xn]print("最短的路径代价为:", node_cost[xn][1])while x0 not in destination_list: xn = node_cost[xn][2] destination_list.append(xn)print("最短路径为:", destination_list)最后的效果: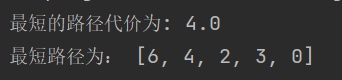
2.整体程序
import numpy as np# ①构建地图mapping_list = [[np.inf for i in range(0, 7)] for i in range(0, 7)] # 构建全是无穷大的二维列表for i in range(0, 7): mapping_list[i][i] = 0 # 对角线处的值为0mapping_list[0][1] = 2mapping_list[0][2] = 3mapping_list[0][3] = 1mapping_list[1][4] = 2mapping_list[2][3] = 1mapping_list[2][4] = 1mapping_list[2][5] = 1mapping_list[3][5] = 3mapping_list[4][5] = 2mapping_list[5][6] = 2mapping_list[1][0] = 2mapping_list[2][0] = 3mapping_list[3][0] = 1mapping_list[3][2] = 1mapping_list[4][1] = 2mapping_list[4][2] = 1mapping_list[4][6] = 1mapping_list[5][2] = 1mapping_list[5][3] = 3mapping_list[5][4] = 2mapping_list[6][5] = 2mapping_list[6][4] = 1mapping_list = np.array(mapping_list) # 将mapping_list转换成数组形式# print(mapping_list)# ② 初始化node_cost = [[np.inf for i in range(0, 3)] for i in range(0, 7)] # 构建全是无穷大的二维列表# arr这个数组用来表示每个节点的[节点名 node_cost 父节点]for i in range(0, 7): node_cost[i][0] = i# 计算A点与它相邻的节点,更新其node_cost和父节点,并且将A点放入close_list里面node0 = 0close_list = []for i in range(0, 7): if mapping_list[int(node0)][i] < node_cost[i][1]: node_cost[i][2] = node0 node_cost[i][1] = mapping_list[int(node0)][i]close_list.append(int(node0))# ③ 构建一系列函数以实现迭代功能# 1、构建函数用来选择node_cost最小的节点# 选择node_cost值最小的节点->node 0def choose_min(node_cost, close_list): node_cost = np.array(node_cost) # 将node_cost从list转换成array open_list = list(set(node_cost[:, 0].tolist()) - set(close_list)) # 建立一个open_list放入没有被遍历的点 final_list = [] for i in open_list: final_list.append(node_cost[int(i)].tolist()) final_list = np.array(final_list) # final_list转换成array,才可以利用np.where找最小值 node0 = final_list[np.where(final_list[:, 1] == final_list[:, 1].min())][0][0] # 将node_cost最小的点的节点名给node0 return int(node0)# -------------------------------------------------------------------------------------------------------# 2、构建count_cost函数用来计算相邻节点的node_cost# 计算node0邻节点的node_cost,此时的node_cost值就是地图上的代价值加上父节点的代价值,如果已经比原来小则更新node_cost和父节点# 并将node0放入close_list里面def count_cost(mapping_list, node_cost, close_list): for i in range(0, 7): if mapping_list[node0][i] + node_cost[node0][1] < node_cost[i][1]: node_cost[i][2] = node0 node_cost[i][1] = mapping_list[node0][i] + node_cost[node0][1] close_list.append(node0) return [node_cost, close_list]# ④ 开始迭代----->迭代中止的条件:终点在close_list里面while 6 not in close_list: node0 = choose_min(node_cost, close_list) # 找node_cost最小的节点 [node_cost, close_list] = count_cost(mapping_list, node_cost, close_list) # 计算邻节点 # print(close_list)xn = 6x0 = 0destination_list = [xn]print("最短的路径代价为:", node_cost[xn][1])while x0 not in destination_list: xn = node_cost[xn][2] destination_list.append(xn)print("最短路径为:", destination_list)