?大家好,我是白晨,一个不是很能熬夜?,但是也想日更的人✈。如果喜欢这篇文章,点个赞?,关注一下?白晨吧!你的支持就是我最大的动力!???

文章目录
?前言?贪心算法经典题目?1.分割平衡字符串?2.买卖股票的最佳时机?3.跳跃游戏?4.多机调度问题?5.活动选择?6.最多可以参加的会议数目?7.无重叠区间 ?总结
?前言
观前提示:此文章需要一定贪心算法的基础。
大家好呀,我是白晨?。
贪心算法算是一种比较耳熟能详的算法,只要求出局部最优解就可以得到整体的最优解,而且面试很喜欢出这种问题。但是,贪心算法其实并不好想,特别是有些问题比较绕的时候,你可能根本就想不到贪心算法。动态规划这个算法是从整体出发求整体最优,而贪心算法是从局部出发求整体最优,所以很多时候贪心算法并不好用,而且动态规划说是难,但是掌握方法后使用起来非常爽,而贪心算法规律比较难找,每一种题都有不同的具体贪心思想。
所以,白晨选出了一些贪心算法的几道经典题目,以帮助大家理解贪心算法。题目难度由低到高,都是比较经典的题型。可能不是很难,但是有些题目很绕,看了答案后,会觉得自己被侮辱了,这就是贪心算法?。
?贪心算法经典题目
?1.分割平衡字符串
原题链接:分割平衡字符串
解析:
这道题要求尽可能多的切割平衡字符串
我们通过观察例题以及推理可得,要想得到最多切割,切割处来的字符串必须为先R后 L 或者先 L后 R 。绝对不能出现 L R 相互交错出现。也就是说分割时,不能出现嵌套。贪心策略: 不要有嵌套的平衡,只要达到平衡,就立即分割故可以定义一个变量 cnt ,在遇到不同的字符时,向不同的方向变化,设 cnt 为 0 时达到平衡,分割数更新。比如:从左往右扫描字符串s,遇到
L , cnt + 1,遇到 R ,cnt - 1当
cnt 为0时即,更新记录平衡字符串子串的变量 ++num class Solution {public: int balancedStringSplit(string s) { int len = s.size(); int cnt = 0, num = 0; for (int i = 0; i < len; ++i) { // 遇到R,--cnt if (s[i] == 'R') --cnt; // 遇到L,++cnt else ++cnt;// 判断:如果cnt等于0,说明要切割 if (cnt == 0) ++num; } return num; }};?2.买卖股票的最佳时机
原题链接:买卖股票的最佳时机
解析:
这道题非常具有迷惑性,也特别容易想复杂,当你看到答案的时候可能会想找个豆腐撞死。
法1:贪心算法
其实你完全没有必要去想怎么买卖才能利益最大化,因为这个题目是给出了后面几天的股价的,所以我们可以到第二天再做决策。
所以,第二天股价涨时,把我们就买入前一天的股票,再前一天的股票卖出,也就是第二天得到了利润
如果第二天跌了,我们第一天就不买入
总结一下就是:
连续上涨交易日: 则第一天买最后一天卖收益最大,等价于每天都买卖
故可以遍历整个股票交易日价格列表,在所有上涨交易日都买卖(赚到所有利润),所有下降交易日都不买卖(永不亏钱)。
class Solution {public: int maxProfit(vector<int>& prices) { int day = prices.size(); int profit = 0; for (int i = 1; i < day; ++i) { // 股价比前一天高就卖出 if (prices[i] > prices[i - 1]) profit += prices[i] - prices[i - 1]; } return profit; }};法二:动态规划
这道题也能用动态规划做,就是很麻烦,而且效果没有贪心好。如果没有学过动态规划的同学可以不用看这种方法。

状态:
定义状态 F ( i , 0 ) F(i,0) F(i,0) 表示第 i 天交易完后手里没有股票的最大利润, F ( i , 1 ) F(i,1) F(i,1)表示第i 天交易完后手里持有一支股票的最大利润。
class Solution {public: int maxProfit(vector<int>& prices) { int day = prices.size(); vector<vector<int> > ret(day, vector<int>(2, 0)); // 第一天的状态 ret[0][0] = 0; ret[0][1] = -prices[0]; for (int i = 1; i < day; ++i) { // 每天选一次 ret[i][0] = max(ret[i - 1][0], ret[i - 1][1] + prices[i]); ret[i][1] = max(ret[i - 1][1], ret[i - 1][0] - prices[i]); } return ret[day - 1][0]; }};优化算法:
因为今天的状态只与前一天的状态有关,所以我们可以用两个局部变量存放前一天的状态。空间复杂度可以由 O ( n ) O(n) O(n) 优化到 O ( 1 ) O(1) O(1) 。class Solution {public: int maxProfit(vector<int>& prices) { int day = prices.size(); int ret[2]; ret[0] = 0; ret[1] = -prices[0]; // 存放昨天的状态 int tmp0 = ret[0]; int tmp1 = ret[1]; for (int i = 1; i < day; ++i) { ret[0] = max(tmp0, tmp1 + prices[i]); ret[1] = max(tmp1, tmp0 - prices[i]); tmp0 = ret[0]; tmp1 = ret[1]; } return ret[0]; }};?3.跳跃游戏
原题链接:跳跃游戏
解析:
贪心策略
设想一下,对于数组中的任意一个位置 y,我们如何判断它是否可以到达?
根据题目的描述,只要存在一个位置x,它本身可以到达,并且它跳跃的最大长度为 x + n u m s [ x ] x + nums[x] x+nums[x],这个值大于等于 y,即 x + n u m s [ x ] ≥ y x+nums[x] ≥ y x+nums[x]≥y ,那么位置 y 也可以到达。
换句话说,对于每一个可以到达的位置 x,它使得 x + 1 , x + 2 , ⋯ , x + n u m s [ x ] x+1, x+2,⋯,x+nums[x] x+1,x+2,⋯,x+nums[x] 这些连续的位置都可以到达。
这样以来,我们依次遍历数组中的每一个位置,并实时维护最远可以到达的位置。对于当前遍历到的位置x,如果它在最远
可以到达的位置的范围内,那么我们就可以从起点通过若干次跳跃到达该位置,因此我们可以用 x + n u m s [ x ] x+nums[x] x+nums[x]更新 最远可以
到达的位置。
在遍历的过程中,如果最远可以到达的位置大于等于数组中的最后一个位置,那就说明最后一个位置可达,我们就可以直接
返回True作为答案。反之,如果在遍历结束后,最后一个位置仍然不可达,我们就返回 False 作为答案。、
以题目中的示例一
[2, 3, 1, 1, 4]
为例:
我们一开始在位置 0,可以跳跃的最大长度为 2,因此最远可以到达的位置被更新为 2;
我们遍历到位置 1,由于 1≤2,因此位置 1 可达。我们用 1加上它可以跳跃的最大长度3,将最远可以到达的位置更新为
4。由于4大于等于最后一个位置4,因此我们直接返回 True。
我们再来看看题目中的示例二
[3, 2, 1, 0, 4]
我们一开始在位置0,可以跳跃的最大长度为3,因此最远可以到达的位置被更新为3;
我们遍历到位置1,由于1≤3,因此位置1可达,加上它可以跳跃的最大长度2得到3,没有超过最远可以到达的位置;
位置 2、位置 3 同理,最远可以到达的位置不会被更新;
我们遍历到位置4,由于4>3,因此位置4不可达,我们也就不考虑它可以跳跃的最大长度了。
在遍历完成之后,位置4仍然不可达,因此我们返回 False
class Solution {public: bool canJump(vector<int>& nums) { int maxLen = 0; int len = nums.size(); for(int i = 0; i < len; ++i) { // 必须要判断前面最大能不能到达这个点 // 能到达才更新,不能到达就不更新 if(i <= maxLen) maxLen = max(i + nums[i], maxLen); // 遇到最大到达距离大于等于最后一个数的下标就返回true if(maxLen >= len - 1) return true; } return false; }};// 改版class Solution {public: bool canJump(vector<int>& nums) { int maxLen = 0; int len = nums.size(); for(int i = 0; i < len; ++i) { // 通过上面的代码,相信很多人已经发现,如果到最大到达距离达不了遍历中的某一个元素 // 那么,最后一定到不了最后一个元素 // 因为最大到达距离是覆盖式的,能到最后一个元素必然可以到达前面的元素 // 所以我们可以先判断是否能到这个元素,能到达就更新,不能到达就直接返回false if(maxLen < i) return false; maxLen = max(i + nums[i], maxLen); }// 遍历完成说明必然可以到达最后一个元素,直接返回true return true; }};?4.多机调度问题
某工厂有 n 个独立的作业,由m台相同的机器进行加工处理。作业 i 所需的加工时间为 ti ,任何作业在被处理时不能中
断,也不能进行拆分处理。现厂长请你给他写一个函数:算出 n 个作业由 m 台机器加工处理的最短时间
贪心思路:
如果 n < = m n <= m n<=m ,那么只需要返回任务中时间最长的一项任务即可如果 n > m n > m n>m 首先,我们可以将任务按时间长短排序,按降序排列。其次,我们针对每一项任务,都要选出当前所有机器中执行任务时间最短的机器来执行。最后,选出执行任务总时间最长的一个机器,返回其执行任务所需要的时间。bool cmp(const int& x, const int& y){return x > y;}int greedStrategy(const vector<int>& works, vector<int>& machines){// 按工作时间长短排序sort(works.begin(), works.end(), cmp);int workNum = works.size();int machineNum = machines.size();// 如果 n <= m ,返回任务中时间最长的一项任务if (workNum <= machineNum)return works[0];// 选择机器执行每一个任务for (int i = 0; i < workNum; ++i){int flag = 0;// 选择现在执行任务花费时间最少的机器for (int j = 1; j < machineNum; ++j){if (machines[j] < machines[flag])flag = j;}// 执行本次任务machines[flag] += works[i];}// 选出用时最长的机器int max = 0;for(int e : machines){ if (e > max)max = e;}// 返回时间return max;}?5.活动选择
有n个需要在同一天使用同一个教室的活动a1, a2, …, an,教室同一时刻只能由一个活动使用。每个活动a[i]都有一个开始时间s[i]和结束时间f[i]。一旦被选择后,活动a[i]就占据半开时间区间[s[i],f[i])。如果[s[i],f[i])和[s[j],f[j])互不重叠,a[i]和a[j]两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量。
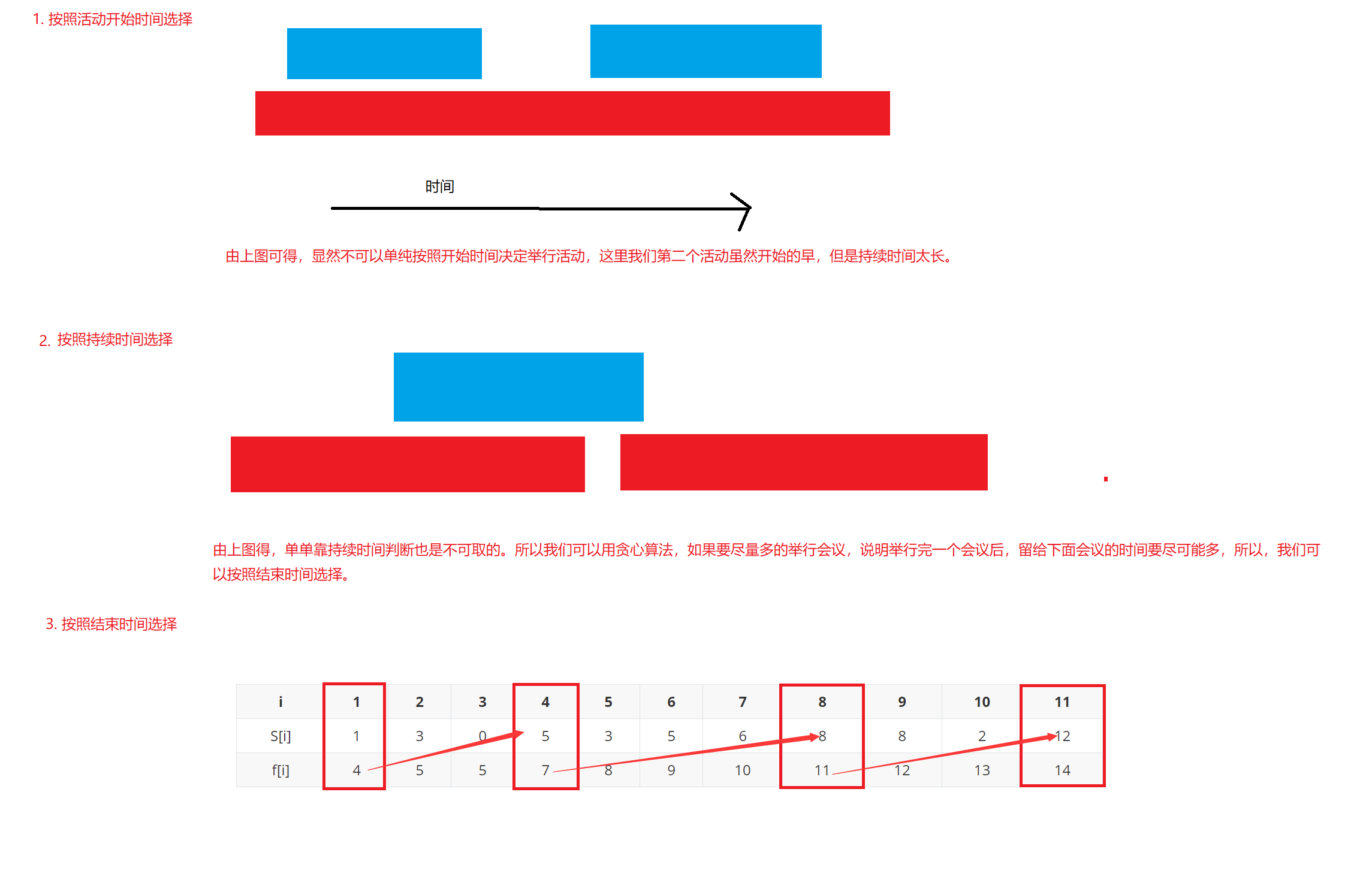
面对活动选择会遇到以下三种情况:
开始时间和结束时间都不同
这里我们选择结束时间早的。
开始时间相同,结束时间不同
这里我们选择结束时间早的
开始时间不同,结束时间相同
bool cmp(const pair<int, int>& a, const pair<int, int>& b){return a.second < b.second;}int greedyActivitySelector(const vector<pair<int, int>>& act){// 按照结束时间从早到晚排序sort(act.begin(), act.end(), cmp);// 记录一个活动的结束时间int end = 1;int num = 0;// 遍历每一个活动for (auto e : act){// 当一个活动的开始时间大于等于前一个被举行活动的结束时间时,执行这个活动if (e.first >= end){end = e.second;++num;}}return num;}?6.最多可以参加的会议数目

原题链接:最多可以参加的会议数目
这个题与上题类似,我们可以使用贪心算法,按照结束时间先后去参加,先结束的先参加。
但是这道题上道题不同的地方在于,会议有持续时间,而且可以只选择一天去,所以多个会议持续时间重叠并可能不影响参加会议,这道题的难度更大。
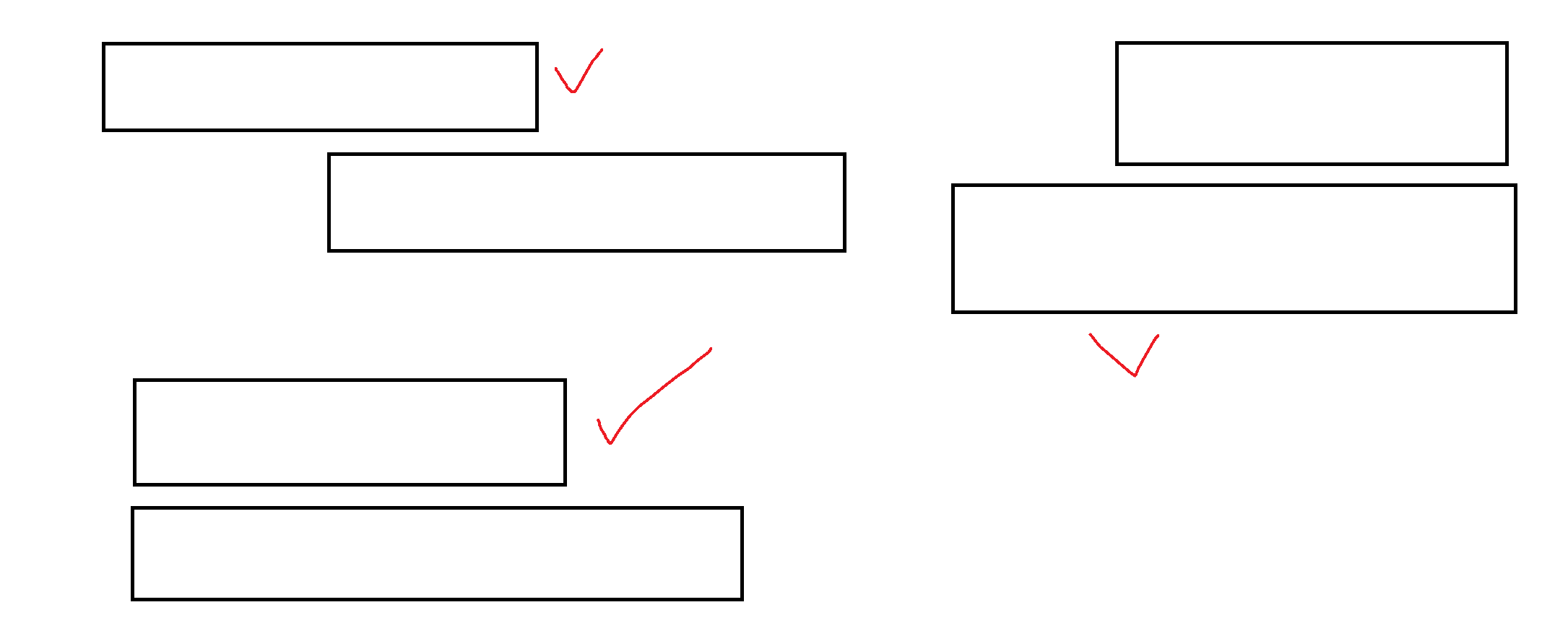
法一:贪心算法硬解
思路详解:
直接莽夫,记录下已经参加会议过的天。每次选择结束最早的会议,遍历这个会议的开始日期到结束日期,判断是否有未参加会议的天,如果有,就参加,如果没有,就不参加。
class Solution {public:int maxEvents(vector<vector<int>>& events) { // 按照结束顺序排升序,如果结束时间相同,就将开始时间早的排在前sort(events.begin(), events.end(), [](vector<int>& a, vector<int>& b) {if (a[1] != b[1]) return a[1] < b[1];return a[0] < b[0];});// 记录参会次数int num = 0; // 创建一个数组,判断这天有没有使用vector<bool> used(100001, false);for (auto e : events){ // 遍历一个会议的开始到结束,判断是否有空闲的天for (int i = e[0]; i <= e[1]; ++i){if (!used[i]){ used[i] = true;++num;break;}}}return num;}};这种方法可以说简单粗暴,但是相应的,时间复杂度取决于题目给的数据,如果给出一组例如 [ 1 , 1 ] , [ 1 , 2 ] , [ 1 , 3 ] , [ 1 , 4 ] . . . . . . . [ 1 , 10000 ] [1,1],[1,2],[1,3],[1,4].......[1,10000] [1,1],[1,2],[1,3],[1,4].......[1,10000]
开始时间相同,但是结束时间不同的数据,每一次都要从开始到结束遍历,时间复杂度非常之高,会导致时间太长而无法通过。
所以,直接莽行不太通。
法二:队列+贪心
思路解析:
这次我们按照开始顺序进行排序,排成升序。然后,从第一天开始走,遇到这天开始的会议按照结束时间加入小根堆,这样可以保证,结束时间早的会议先被使用。其次,由于一天只能参加一个会议,所以有些会议可能参加不了,如 [[1,4],[4,4],[2,2],[3,4],[1,1]] ,里面的 [ 4 , 4 ] [4,4] [4,4] 就因为前面的会议太多,第四天参加不了,第五天会议已经结束而被迫放弃这个会议。所以,我们每天要放弃掉已经过时的会议。接下来,选出小根堆的堆顶,也就是选择结束时间最早的那一个会议参加。重复 2~4 步,直到堆为空。class Solution {public:int maxEvents(vector<vector<int>>& events) {priority_queue<int, vector<int>, greater<int>> pq;sort(events.begin(), events.end());int curDay = 1;int i = 0;int n = events.size();int ans = 0;while (i < n || !pq.empty()) {// 队列存储已经开始的会议, 按结束时间小根堆排序 while (i < n && events[i][0] == curDay) {pq.push(events[i][1]);i++;}// 已经结束的会议出堆while (!pq.empty() && pq.top() < curDay) {pq.pop();}// 贪心思想, 选择最早结束的会议参加 if (!pq.empty()) {pq.pop();ans++;}curDay++;}return ans;}};?7.无重叠区间
原题链接:无重叠区间
法一:
要求最小移除的区间数,也就是求最大不重叠的区间,所以我们可以按照活动选择的方法,先求出最大不重叠区间数,再用总区间数减去最大不重叠区间数,就可以得到最小移除的区间数。
class Solution {public:static bool cmp(const vector<int>& a, const vector<int>& b){return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0)return 0; // 按结束时间从早到晚排序sort(intervals.begin(), intervals.end(), cmp); // 由于区间可能为负,并且第一个结束的区间一定是我们选择的不重叠的,所以我们这里先记录第一个区间 // 记录不重叠区间的数量int num = 1; // 记录上一个不重叠区间的结束int end = intervals[0][1];for (int i = 1; i < intervals.size(); ++i){ // 如果上一个不重叠区间的结束小于等于这个区间的开始,这个区间为不重叠区间if (end <= intervals[i][0]){end = intervals[i][1];++num;}}return intervals.size() - num;}};当然,这个题也可以用范围for
class Solution {public:static bool cmp(const vector<int>& a, const vector<int>& b){return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0)return 0;sort(intervals.begin(), intervals.end(), cmp);int num = 0; // 把end设置为int类型的最小值int end = INT_MIN;for (auto e : intervals){if (end <= e[0]){end = e[1];++num;}}return intervals.size() - num;}};这种方法时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) ,可以说已经是这个题最简单的算法。
法二:
根据题目求解:
如果我们按照起点对区间进行排序,贪心算法就可以起到很好的效果。
贪心策略:
当按照起点先后顺序考虑区间的时候。我们利用一个 prev 指针追踪刚刚添加到最终列表中的区间。遍历的时候,可能遇到图中的三种情况:
当前考虑的两个区间不重叠:

在这种情况下,不移除任何区间,将 prev 赋值为后面的区间,移除区间数量不变。
情况二:两个区间重叠,后一个区间的终点在前一个区间的终点之前:
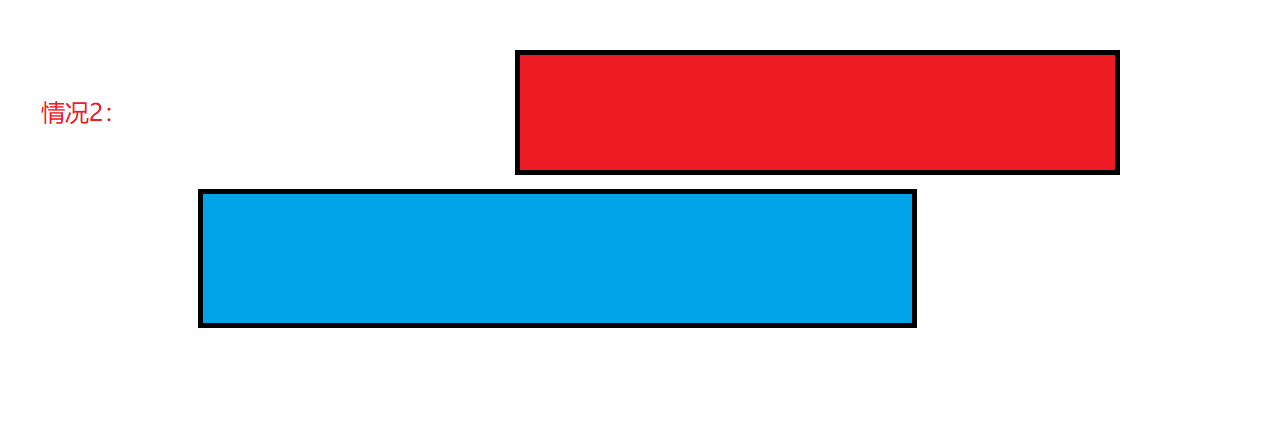
这种情况下,我们可以简单地只用后一个区间。这是显然的,因为后一个区间的长度更小,可以留下更多的空间(AA 和BB),容纳更多的区间。因此, prev 更新为当前区间,移除区间的数量 + 1。
情况三:
两个区间重叠,后一个区间的终点在前一个区间的终点之后:

这种情况下,我们用贪心策略处理问题,直接移除后一个区间。这样也可以留下更多的空间,容纳更多的区间。因此,prev不变,移除区间的数量 + 1。
class Solution {public:static bool cmp(const vector<int>& a, const vector<int>& b){//按起点递增排序if (a[0] != b[0])return a[0] < b[0];return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.empty())return 0; // 排序sort(intervals.begin(), intervals.end(), cmp); // 删除的个数int Dnum = 0; // 保存前一个不重叠区间的下标int prev = 0;for (int i = 1; i < intervals.size(); ++i){ // 当区间重叠时if (intervals[prev][1] > intervals[i][0]){ // 判断是否为情况2if (intervals[prev][1] > intervals[i][1]){prev = i;}++Dnum;} //情况3else{prev = i;}}return Dnum;}};?总结
我们简单总结一下贪心算法的解题过程:
建立数学模型来描述问题;把求解的问题分成若干个子问题;对每一子问题求解,得到子问题的局部最优解;把子问题的局部最优解合成原来解问题的一个解这是一个新的系列 ——【刷题日记】,白晨开这个系列的初衷是为了分享一些不同算法经典题型,以便于大家更好的学习编程。如果大家喜欢这个专栏的话——点击查看【刷题日记】所有文章。
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦?!
如果这篇文章有帮到你,还请给我一个大拇指 ?和小星星 ⭐️支持一下白晨吧!喜欢白晨【刷题日记】系列的话,不如关注?白晨,以便看到最新更新哟!!!
我是不太能熬夜的白晨,我们下篇文章见。