目录

引子：AVL树是因为什么出现的？

1.AVl树的的特性

2.AVl树的框架

3.AVL树的插入 

         3.1四种旋转（左单旋、右单旋、左右双旋、右左双旋）

        3.1.1左单旋

        3.1.2右单旋

         3.1.3左右双旋

         3.1.4右左双旋 

 总结

---

引子：AVL树是因为什么出现的？

二叉搜索树可以缩短查找的效率，如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下时间复杂度：O(N)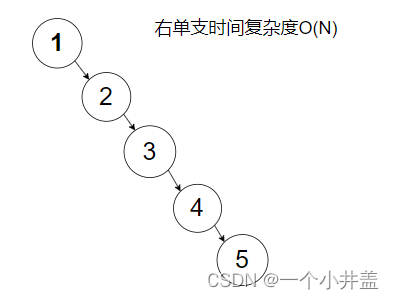

 两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(对树中的结点进行调整),即为AVl树以他们的名字缩写命名也可以叫高度二叉搜索树

1.AVl树的的特性

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树，它就是AVL树。

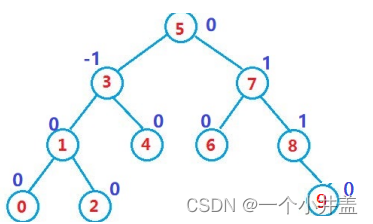
它的左右子树都是AVL树左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)，节点右子树最长路径-左子树最长路径

如果AVl树有n个结点，其高度可保持在O(logN) ，搜索时间复杂度O(logN),为什么？

答：左右子树高度之差的绝对值不超过1，那么只有最后一层会差一部分的节点；

2.AVl树的框架

template<class K, class V>struct AVLtreeNode{    //节点构造函数AVLtreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_kv(kv){}    //节点的成员    //三叉链AVLtreeNode<K, V>* _left;AVLtreeNode<K, V>* _right;AVLtreeNode<K, V>* _parent;int _bf;//平衡因子    //数据使用库里面的pair类存储的kvpair<K, V> _kv;};template<class K,class V>class AVLtree{typedef AVLtreeNode<K, V> Node;public:    //构造函数AVLtree():_root(nullptr){}    //四种旋转void RotateL(Node* parent)void RotateR(Node* parent)void RotateLR(Node* parent)void RotateRL(Node* parent)    //插入bool Insert(const pair<K, V>& kv)    //寻找Node* Find(const K& kv)private:Node* _root;};

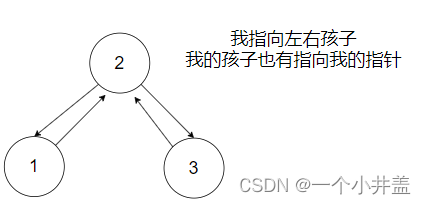
三叉链是什么？

3.AVL树的插入 

bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = _root, *cur = _root;while (cur){//找nulptr，如果已经有这个key了，二叉搜索树的特性不支持冗余，所以返回失败if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first <kv.first){parent = cur;cur = cur->_right;}else{return false;}}//cur = new Node(kv);//判断孩子在父亲的左边还是右边if (cur->_kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent){//影响一条路径所有的祖先if (parent->_right == cur)parent->_bf++;elseparent->_bf--;if (parent->_bf == 0){//左右平衡了不会再影响祖先了break;}if (parent->_bf == 1 || parent->_bf == -1){//当前节点所在子树变了，会影响父亲// 继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//parent所在子树已经不平衡，需要旋转处理一下if (parent->_bf == -2){if (cur->_bf == -1)// 右单旋RotateR(parent);else // cur->_bf == 1RotateLR(parent);}else // parent->_bf  == 2{if (cur->_bf == 1)// 左单旋RotateL(parent);else // cur->_bf == -1RotateRL(parent);}break;}else{// 插入节点之前，树已经不平衡了，或者bf出错。需要检查其他逻辑assert(false);}}return true;}

插入整体逻辑：

如果还没有元素是一课空树，直接插入即可；如果有元素，按pair的first(key)和比较的节点比较结果为大说明为空的哪个位置在右边，和比较的节点比较的结果小说明为空的哪个位置在左边，如果相等说明已经有这个元素了，二叉搜索树不支持冗余返回一个pair类第一个成员为那个相同元素的map的迭代器和第二个成员为false的pair类迭代器；不知道这个已经找到的位置在父节点的左边还是右边，需要判断一下，然后插入元素；插入元素的后那么平衡因子将发生变化，为0说明这个父亲节点左右平衡不会影响其他节点，为1或者-1需要向上调整，为2或者-2说明已经不平衡需要旋转；节点右子树最长路径-左子树最长路径，右边插入节点就+，左边插入节点就-；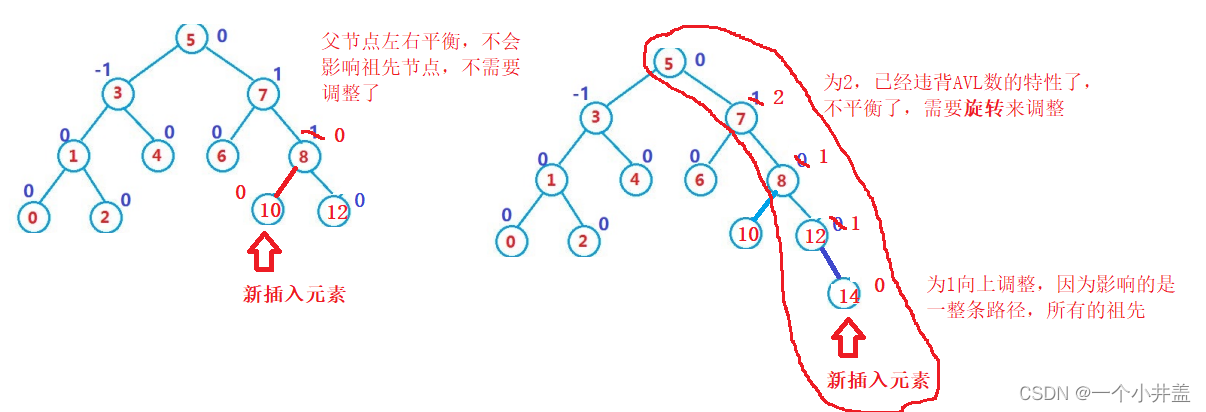

 3.1四种旋转（左单旋、右单旋、左右双旋、右左双旋）

3.1.1左单旋

调用函数是传的参数是轴点要保留轴点的父亲，以及调整三叉链调整后原来的孩子和父亲（轴点）的平衡因子都置为0；

void RotateR(Node* parent){//轴点的左，孩子节点Node* subL = parent->_left;//孩子节点的右Node* subLR = subL->_right;//我的右当你（轴点）的左parent->_left = subLR;//调整三叉链if (subLR)subLR->_parent = parent;//你（轴点）做我的右subL->_right = parent;//调整三叉链Node* parentParent = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{//轴点的父亲新的孩子节点if (parentParent->_left == parent)parentParent->_left = subL;elseparentParent->_right = subL;subL->_parent = parentParent;}subL->_bf = parent->_bf = 0;}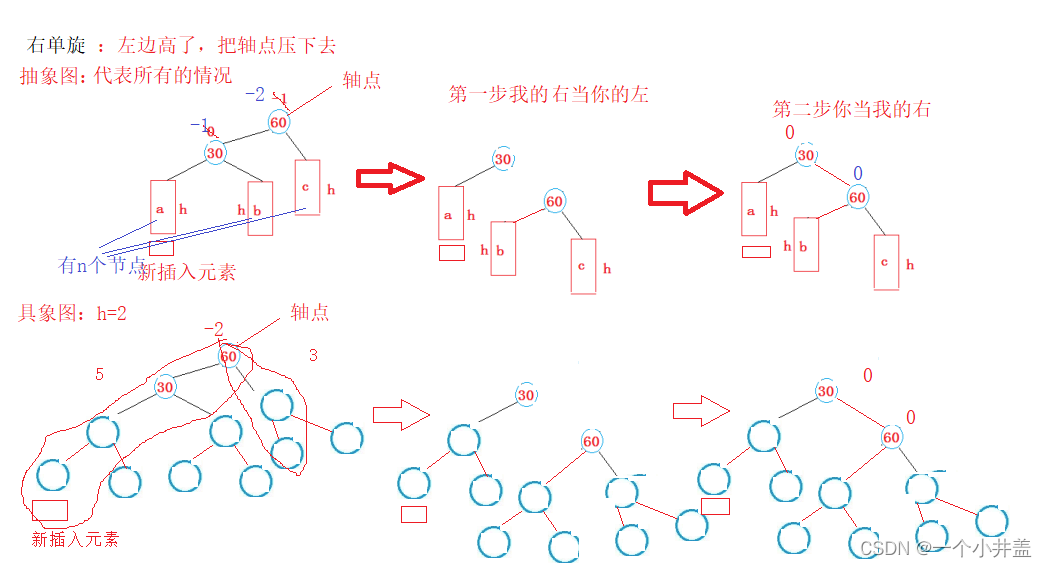

3.1.2右单旋

调用函数是传的参数是轴点要保留轴点的父亲，以及调整三叉链调整后原来的孩子和父亲（轴点）的平衡因子都置为0；

void RotateL(Node* parent){//轴点的右，孩子节点Node* subR = parent->_right;//孩子节点的左Node* subRL = subR->_left;//我的左当你（轴点）的右parent->_right = subRL;//调整三叉链if (subRL){subRL->_parent = parent;}//你（轴点）做我的左subR->_left = parent;Node* parentparent = parent->_parent;parent->_parent = subR;if (parent == _root){if (parentparent->_left == parent)parentparent->_left = subR;elseparentparent->_right = subR;subR->_parent = parentparent;}else{subR->_parent = nullptr;_root = subR;}subR->_bf = parent->_bf = 0;}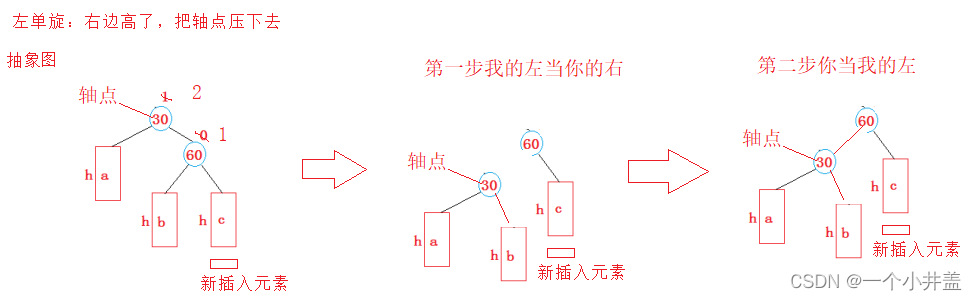

 

 3.1.3左右双旋

调用左单旋是传的参数是轴点1，右单旋传的轴点2平衡因子分3种情况，依靠3个被改变节点中最后一个来判断

void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);// ...平衡因子调节还需要具体分析if (bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}

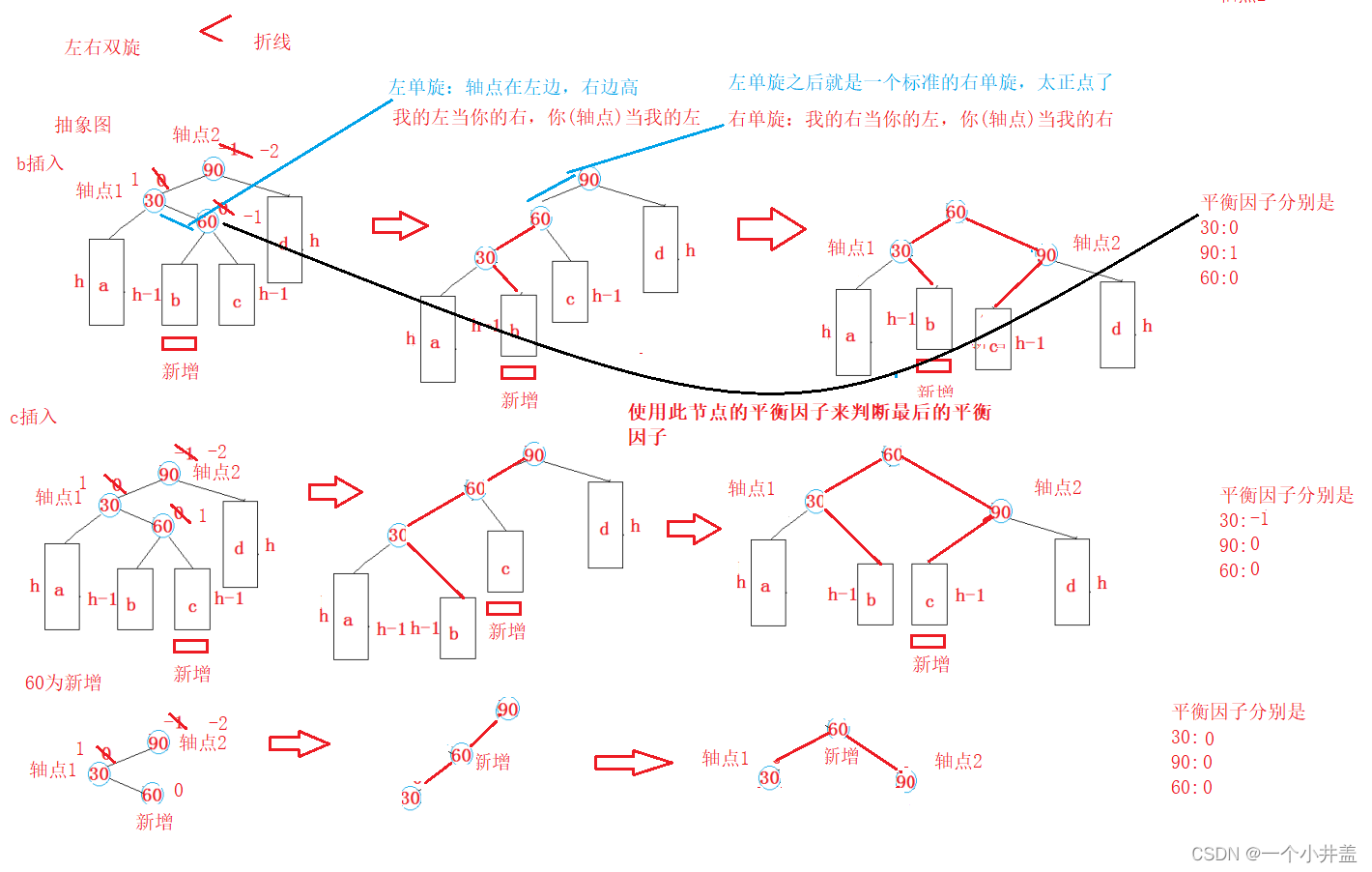
依靠3个被改变节点中最后一个来判断

 

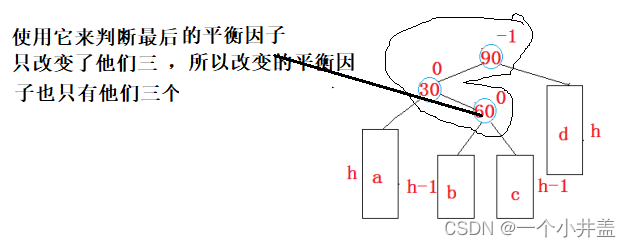
 3.1.4右左双旋 

调用右单旋是传的参数是轴点1，左单旋传的轴点2平衡因子分3种情况，依靠3个被改变节点中最后一个来判断

void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);// 平衡因子更新if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}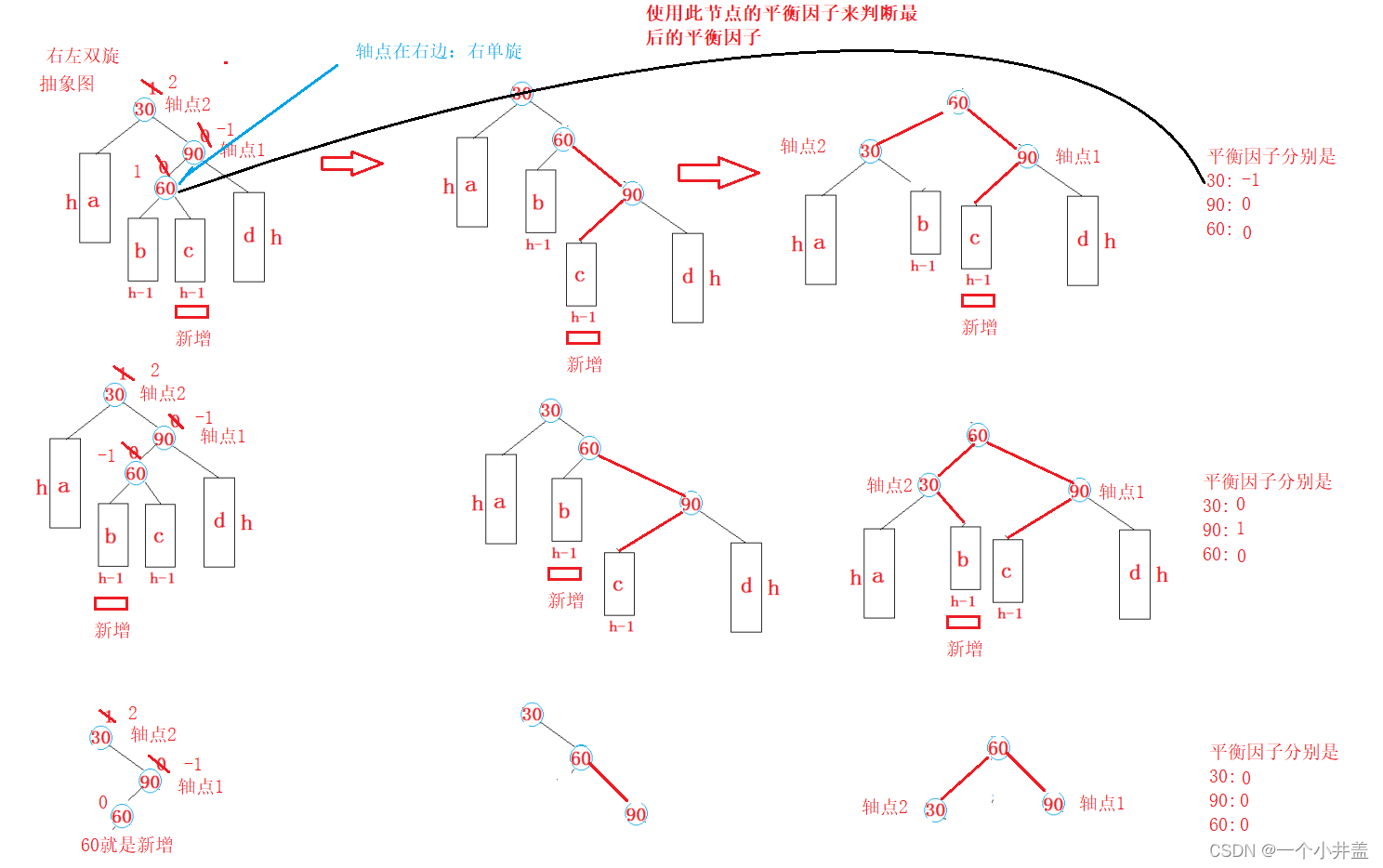

 总结

调用旋转的实参是轴点左单旋：我的左当你的右，你（轴点）当我的左右单旋：我的右当你的左，你（轴点）当我的右