对三维空间进行三角剖分的大体逻辑思路和流程同二维空间的三角剖分是一样的,二维的代码实践过程可以前往本专栏的第一篇文章:二维 二维空间的三角剖分。
在理清楚二维平面下三角剖分的思路之后,我们尝试将其中的一些概念升级一个维度。
我们先来分析Delaunay三角剖分从二维空间到三维空间过程中的一些变化:
1.剖分成若干个三角形单元——剖分成若干个四面体单元
2.根据x、y排序点集——根据x、y、z排序点集
3.根据排序好的点集构建超级三角形——根据排序好的点集构建超级四面体
4.构造用于缓存边数据的列表——构造用于缓存面数据的列表
5.计算每个三角形的外接圆,判断该三角形与点之间的空间关系——计算每个四面体的外接球,判断该四面体与点之间的空间关系
6.最终得到一个三角形列表——最终得到一个四面体列表
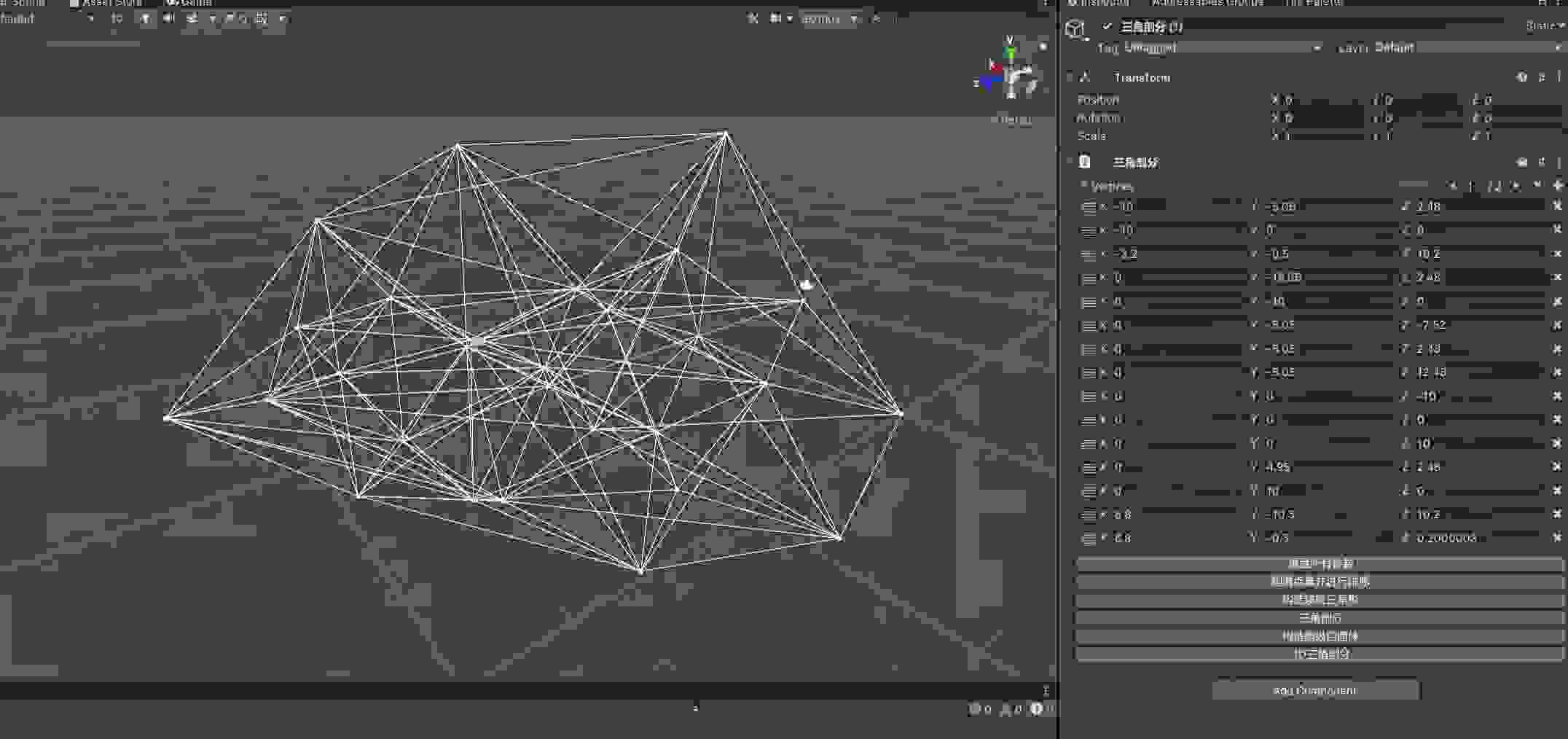
先上效果图(图为Unity中用Gizmos将每个四面体单元顶点连线画出来的预览图):
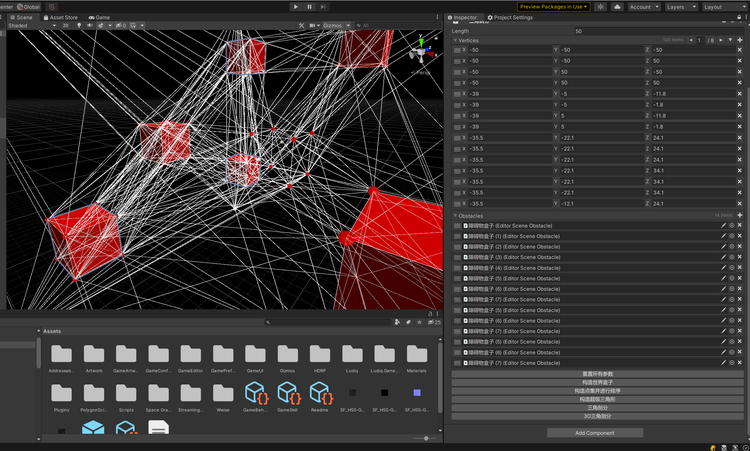
尝试加入障碍物AABB包围盒后进行剖分,并用Mesh网格渲染显现:

一、输入与输出
输入:
/// <summary> /// 点集 /// </summary> public List<Vector3> _vertices = new List<Vector3>();输出:
/// <summary> /// 四面体列表 /// </summary> List<Tetrahedron> _tetrahedron = new List<Tetrahedron>();二、所需要自定义的类:
1.Surface类:存放四面体每一个面的数据
用三个Vector3来定义一个三角形面:
public class Surface { public Vector3 P1; public Vector3 P2; public Vector3 P3; public Surface(Vector3 P1,Vector3 P2,Vector3 P3) { this.P1 = P1; this.P2 = P2; this.P3 = P3; } }2.Tetrahedron类:存放每个四面体单元的数据
首先是参数和构造函数:
参数包括四面体的四个顶点和四个三角形面、外接球球心、外接球半径以及一个判断是否为可用四面体的bool值;
构造函数传入的参数为一个顶点和一个三角形面,即以一个顶点和一个已存在的三角形面生成一个新的四面体;
public class Tetrahedron { public Vector3 P1; public Vector3 P2; public Vector3 P3; public Vector3 P4; public Vector3 Center; public double R; public Surface E1; public Surface E2; public Surface E3; public Surface E4; public bool isBad; public Tetrahedron(Vector3 V, Surface P) { P1 = V; P2 = P.P1; P3 = P.P2; P4 = P.P3; GetTetrahedronExcenterRadius(); SurfaceValue(); }}其次是四面体类中的一些计算函数:
(1).计算该四面体的外接球:
/// <summary> /// 计算四面体的外接球 /// </summary> public void GetTetrahedronExcenterRadius() { float x1 = P1.x; float x2 = P2.x; float x3 = P3.x; float x4 = P4.x; float y1 = P1.y; float y2 = P2.y; float y3 = P3.y; float y4 = P4.y; float z1 = P1.z; float z2 = P2.z; float z3 = P3.z; float z4 = P4.z; float a11 = x2 - x1; float a12 = y2 - y1; float a13 = z2 - z1; float b1 = (float)0.5 * ((x2 - x1) * (x2 + x1) + (y2 - y1) * (y2 + y1) + (z2 - z1) * (z2 + z1)); float a21 = x3 - x1; float a22 = y3 - y1; float a23 = z3 - z1; float b2 = (float)0.5 * ((x3 - x1) * (x3 + x1) + (y3 - y1) * (y3 + y1) + (z3 - z1) * (z3 + z1)); float a31 = x4 - x1; float a32 = y4 - y1; float a33 = z4 - z1; float b3 = (float)0.5 * ((x4 - x1) * (x4 + x1) + (y4 - y1) * (y4 + y1) + (z4 - z1) * (z4 + z1)); float temp = a11 * (a22 * a33 - a23 * a32) + a12 * (a23 * a31 - a21 * a33) + a13 * (a21 * a32 - a22 * a31); float x0 = ((a12 * a23 - a13 * a22) * b3 + (a13 * a32 - a12 * a33) * b2 + (a22 * a33 - a23 * a32) * b1) / temp; float y0 = -((a11 * a23 - a13 * a21) * b3 + (a13 * a31 - a11 * a33) * b2 + (a21 * a33 - a23 * a31) * b1) / temp; float z0 = ((a11 * a22 - a12 * a21) * b3 + (a12 * a31 - a11 * a32) * b2 + (a21 * a32 - a22 * a31) * b1) / temp; float radius = (float)Math.Sqrt((x0 - x1) *2 + (y0 - y1) * 2 + (z0 - z1) * 2); Center = new Vector3(x0,y0,z0); R = GetDistance(P1, Center); } private double GetDistance(Vector3 A, Vector3 B) { return Math.Sqrt(Math.Pow((A.x - B.x), 2) + Math.Pow((A.y - B.y), 2) + Math.Pow((A.z - B.z), 2)); }(2).判断该四面体与一个点之间的空间关系:
public bool isComtain(Vector3 node) { GetTetrahedronExcenterRadius(); if ((node - Center).sqrMagnitude <= R * R) return true; else return false; }(3).通过一个点与一个面构造出四面体后,对该四面体中的面参数进行赋值:
public void SurfaceValue() { E1 = new Surface(P1, P2,P3); E2 = new Surface(P1,P2, P4); E3 = new Surface(P1, P3,P4); E4 = new Surface(P2, P3,P4); }(4).检查该四面体是否包含超级四面体中的顶点(若包含的话最后要从四面体列表中删去)
public void Check(Tetrahedron s) { Vector3[] su = new Vector3[4]; su[0] = s.P1; su[1] = s.P2; su[2] = s.P3; su[3] = s.P4; if (su.Contains(P1) || su.Contains(P2) || su.Contains(P3)|| su.Contains(P4)) isBad = true; int i; float ans; Vector3 s1, s2, s3; for (i = 0; i < 4; i++) { s1.x = su[1].x - su[0].x; s1.y = su[1].y - su[0].y; s1.z = su[1].z - su[0].z; s2.x = su[2].x - su[0].x; s2.y = su[2].y - su[0].y; s2.z = su[2].z - su[0].z; s3.x = su[3].x - su[0].x; s3.y = su[3].y - su[0].y; s3.z = su[3].z - su[0].z; ans = s1.x * s2.y * s3.z + s1.y * s2.z * s3.x + s1.z * s2.x * s3.y - s1.z * s2.y * s3.x - s1.x * s2.z * s3.y - s1.y * s2.x * s3.z; if (ans == 0) isBad = true; } }三、Delaunay 二维三角剖分过程
1.变量
#region 3D三角剖分参数 /// <summary> /// 点集 /// </summary> public List<Vector3> _vertices = new List<Vector3>(); /// <summary> /// 超级四面体 /// </summary> Tetrahedron SuperTetrahedron; /// <summary> /// 面列表 /// </summary> List<Surface> _surface = new List<Surface>(); /// <summary> /// 三角形列表 /// </summary> List<Tetrahedron> _tetrahedron = new List<Tetrahedron>(); #endregion2.剖分过程:
(1)第一步:对输入的点集进行排序(根据x,y,z依次进行排序):
_vertices = _vertices.OrderBy(o => o.x).ThenBy(o => o.y).ThenBy(o => o.z).ToList();(2)第二步:根据排序好的点集构建超级四面体(即找到并构造出包含点集中所有节点的四面体):
SuperTetrahedron = FindSuper_Tetrahedron(_vertices); /// <summary> /// 找到超级四面体 /// </summary> /// <returns></returns> public Tetrahedron FindSuper_Tetrahedron(List<Vector3> _vertices) { Vector3 Circle; float Radius; float xmin = _vertices[0].x; float xmax = _vertices[_vertices.Count - 1].x; float ymin = _vertices[0].y; float ymax = _vertices[_vertices.Count - 1].y; float zmin = _vertices[0].z; float zmax = _vertices[_vertices.Count - 1].z; foreach (var dot in _vertices) { if (ymin > dot.y) ymin = dot.y; if (ymax <= dot.y) ymax = dot.y; if (zmin > dot.z) zmin = dot.z; if (zmax <= dot.z) zmax = dot.z; } Vector3 P1 = new Vector3(xmin, ymin, zmin); Vector3 P3 = new Vector3(xmax, ymax, zmax); Circle = (P1 + P3) / 2; Radius = Mathf.Sqrt((P1 - P3).sqrMagnitude); Vector3 sP1 = Circle + new Vector3(0, Radius * 3, 0); Vector3 sP2 = Circle + new Vector3(0, -Radius, Radius * 2 * Mathf.Sqrt(2)); Vector3 sP3 = Circle + new Vector3(Radius * Mathf.Sqrt(6), -Radius, -Radius * Mathf.Sqrt(2)); Vector3 sP4 = Circle + new Vector3(-Radius * Mathf.Sqrt(6), -Radius, -Radius * Mathf.Sqrt(2)); Tetrahedron super_Tetrahedron = new Tetrahedron(sP1, new Surface(sP2,sP3,sP4)); //Debug.LogError((sP1+sP2+sP3+sP4)/4); return super_Tetrahedron; }同样是用笨笨的方法(逻辑类似于构造AABB包围盒的思路),这一步有待改进;
(3)第三步:剖分三维空间!
剖分的过程和二维的思路一样,从超级四面体开始,找到存在与四面体外接球内的点对该四面体进行分解重构:
首先将刚刚构造好的超级四面体的四个顶点加入点集列表:
_vertices.Add(SuperTetrahedron.P1); _vertices.Add(SuperTetrahedron.P2); _vertices.Add(SuperTetrahedron.P3); _vertices.Add(SuperTetrahedron.P4);先别着急剖分!记得先初始化四面体列表和面缓存列表,然后将超级四面体加入四面体列表:
_tetrahedron.Clear(); _surface.Clear(); _tetrahedron.Add(SuperTetrahedron);然后就可以大刀阔斧的进行剖分啦!循环走起!
for (int i = 0; i < _vertices.Count; i++) { _surface.Clear(); int index = 0; while (index < _tetrahedron.Count) { if (_tetrahedron[index].isComtain(_vertices[i])) { AddSurface(_surface, _tetrahedron[index].E1); AddSurface(_surface, _tetrahedron[index].E2); AddSurface(_surface, _tetrahedron[index].E3); AddSurface(_surface, _tetrahedron[index].E4); _tetrahedron.Remove(_tetrahedron[index]); } else { index++; } } foreach (var e in _surface) { Tetrahedron Ttemp = new Tetrahedron(_vertices[i], e); _tetrahedron.Add(Ttemp); } }还记得二维剖分中的AddEdge()函数吗?三维剖分中的AddSurface()函数也是一样的:
public void AddSurface(List<Surface> _surface, Surface E) { bool isAdd = true; int index = 0; while (index < _surface.Count) { if (_surface[index].P1 == E.P1 && _surface[index].P2 == E.P2 && _surface[index].P3 == E.P3 || _surface[index].P1 == E.P1 && _surface[index].P2 == E.P3 && _surface[index].P3 == E.P2 || _surface[index].P1 == E.P3 && _surface[index].P2 == E.P2 && _surface[index].P3 == E.P1 || _surface[index].P1 == E.P2 && _surface[index].P2 == E.P1 && _surface[index].P3 == E.P3 || _surface[index].P1 == E.P2 && _surface[index].P2 == E.P3 && _surface[index].P3 == E.P1 || _surface[index].P1 == E.P3 && _surface[index].P2 == E.P1 && _surface[index].P3 == E.P2) { _surface.Remove(_surface[index]); isAdd = false; } else { index++; } } if (isAdd) { _surface.Add(E); } }剖分完成后,我们开始筛查哪些四面体用了超级四面体的四个顶点,因为这四个顶点是我们构造出来的本来是不存在的,所以我们要将这些四面体删去:
int Tindex = 0; while (Tindex < _tetrahedron.Count) { _tetrahedron[Tindex].Check(SuperTetrahedron); if (_tetrahedron[Tindex].isBad) _tetrahedron.Remove(_tetrahedron[Tindex]); else Tindex++; }最后,记得移去超级四面体的四个顶点和超级四面体本身:
_tetrahedron.Remove(SuperTetrahedron); _vertices.Remove(SuperTetrahedron.P1); _vertices.Remove(SuperTetrahedron.P2); _vertices.Remove(SuperTetrahedron.P3); _vertices.Remove(SuperTetrahedron.P4);三维空间的三角初步剖分就完成了:
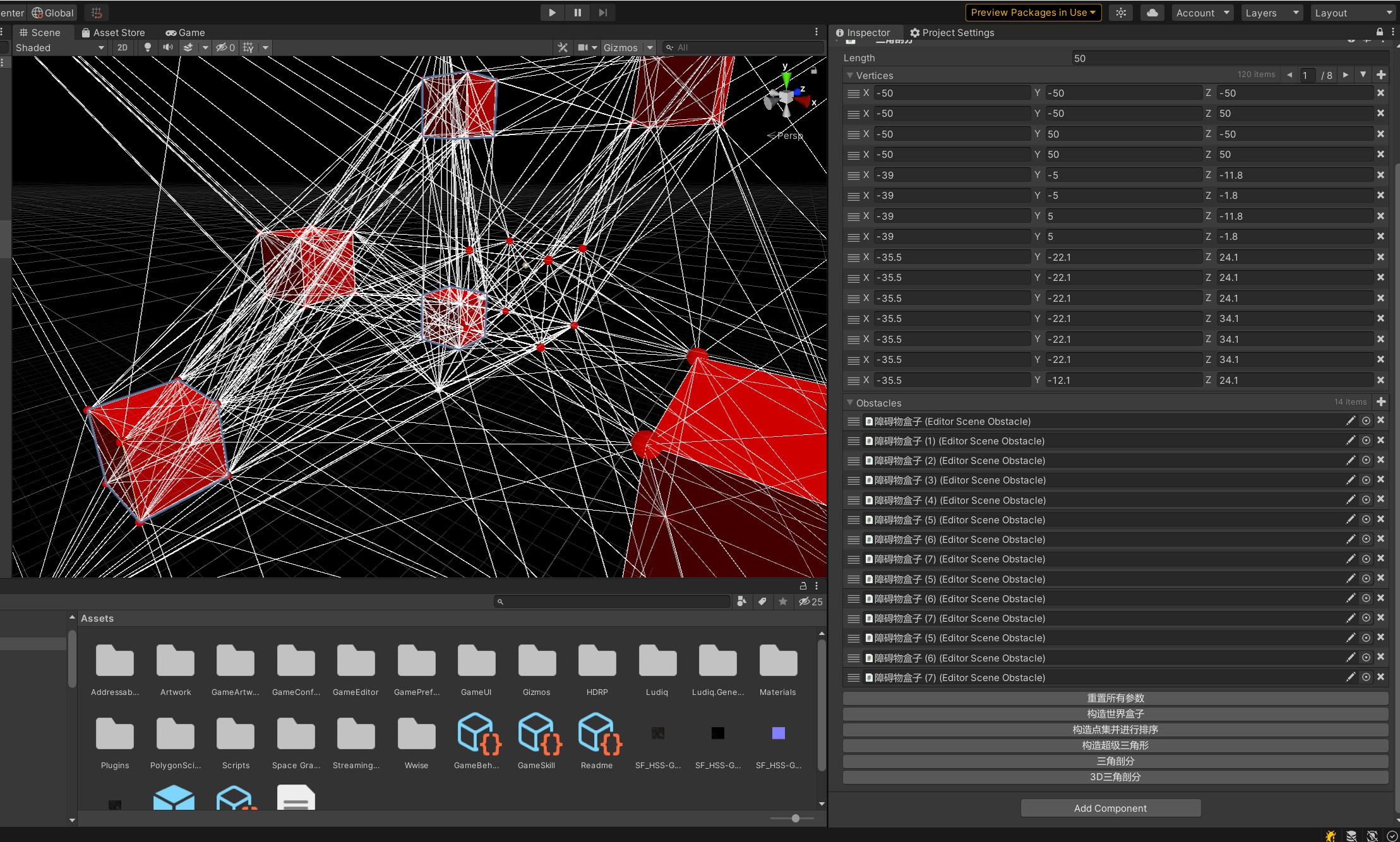
不过目前的三维空间剖分是不完美的,因为在这样的剖分情况下会在很多情况下产生细而长的四面体,这是我们不希望得到的四面体,所以目前方案还需进行优化。