文章目录
第一题: 剑指 Offer 57. 和为s的两个数字解题思路:代码实现: 第二题: 剑指 Offer 57 - II. 和为s的连续正数序列解题思路:代码实现: 第三题: 剑指 Offer 58 - I. 翻转单词顺序解题思路:代码实现: 第四题: 剑指 Offer 59 - I. 滑动窗口的最大值解题思路:代码实现: 第五题: 剑指 Offer 59 - II. 队列的最大值解题思路:代码实现: 第六题: 剑指 Offer 60. n个骰子的点数解题思路:代码实现: 第七题: 剑指 Offer 61. 扑克牌中的顺子解题思路:代码实现:
第一题: 剑指 Offer 57. 和为s的两个数字
LeetCode: 剑指 Offer 57. 和为s的两个数字
添加链接描述
描述:
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。

解题思路:
这里题目中说数组nums 是递增排序. 可以使用双指针的方法用 left 指向 0 下标, 用 right 指向 nums.length-1 下标如果 nums[left] + nums[right] > target , 此时和大了, 就选择小的数字, 让 right--如果 nums[left] + nums[right] < target , 此时和小了, 就选择大的数组, 让 left++如果此时 nums[left] + nums[right] = target , 返回该下标的值.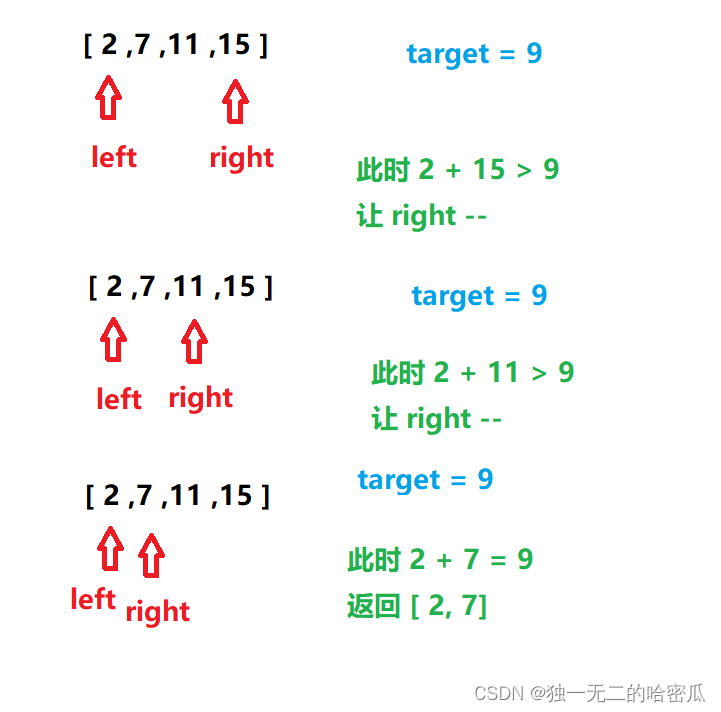
代码实现:
class Solution { public int[] twoSum(int[] nums, int target) { int left = 0; int right = nums.length-1; while(left < right) { int total = nums[left] + nums[right]; if (total > target) { right--; }else if(total < target) { left++; }else{ return new int[]{nums[left],nums[right]}; } } return new int[]{}; }}第二题: 剑指 Offer 57 - II. 和为s的连续正数序列
LeetCode: 剑指 Offer 57 - II. 和为s的连续正数序列
描述:
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
解题思路:
这里也是使用双指针的办法.让left = 1, 让 right=2, 从1, 2开始遍历数学中 1~n 求和, 高斯定理, (n + 1) * (n - 1 + 1) / 2, 所以求得 [left , right] 的和为, (right+left) * (right-left+1) / 2如果当前求的和 total > target, 让 left++如果当前求的和 total < target, 让 right++如果当前求的和 total = target, 将 [left,right] 加入结果集中.并让 left++(否则无法跳出循环) 代码实现:
class Solution { public int[][] findContinuousSequence(int target) { List<int[]> res = new ArrayList<>(); int left = 1; int right = 2; while(left < right) { int total = (right + left) * (right - left + 1) / 2; if(total > target) { left++; }else if(total < target){ right++; }else{ int[] tmp = new int[right-left+1]; for(int i = 0; i < tmp.length; i++) { tmp[i] = i + left; } res.add(tmp); left++; } } int[][] ans = new int[res.size()][]; for(int i = 0; i < res.size(); i++) { ans[i] = res.get(i); } return ans; }}第三题: 剑指 Offer 58 - I. 翻转单词顺序
LeetCode: 剑指 Offer 58 - I. 翻转单词顺序
描述:
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串"I am a student. “,则输出"student. a am I”。

解题思路:
对于本题, 首先对字符串进行去除首尾多余的空格.然后根据空格,拆分成字符串数组然后从后到前遍历, 记住, 可能出现多个空格的情况,如果当前字符串为空, continue5, 不为空, 直接添加当前的字符串, 然后注意添加空格的情况
代码实现:
class Solution { public String reverseWords(String s) { s = s.trim(); String[] str = s.split(" "); StringBuilder sb = new StringBuilder(); for(int i = str.length-1; i >=0; i--) { if(str[i].equals("")) continue; sb.append(str[i]); if(i != 0) { sb.append(" "); } } return sb.toString(); }}第四题: 剑指 Offer 59 - I. 滑动窗口的最大值
LeetCode: 剑指 Offer 59 - I. 滑动窗口的最大值
描述:
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。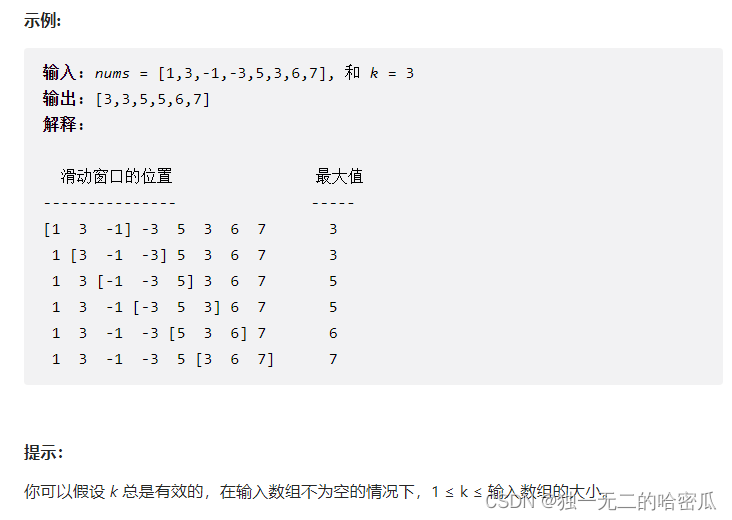
解题思路:
这里构造一个大小为 k 的滑动窗口如果当前滑动窗口的左边界, 不在初始位置, 且 该窗口的右边界 > 前一个窗口的最大值, 那么直接让这个窗口的最大值等于前一个窗口的最大值.如果当前滑动窗口的左边界不在初始位置, 且 该窗口的左边界的前一个值,小于前一个窗口的最大值, 那么, 就让该窗口的最大值等于前一个窗口的最小值.(因为新加入的值, 没有前一个窗口的最大值大, 要丢弃的值, 要比前一个窗口的最大值要小, 那么, 这个最大值就没有改变)不满足2, 3 就直接遍历查找最大值.最后返回每一个窗口的最大值.
代码实现:
class Solution { public int[] maxSlidingWindow(int[] nums, int k) { if(nums.length == 0) return new int[]{}; int left = 0; int right = k - 1; int[] ans = new int[nums.length-k+1]; while (right < nums.length) { if(left > 0 && nums[right] > ans[left-1]) { ans[left] = nums[right]; }else if(left > 0 && nums[left-1] < ans[left-1]){ ans[left] = ans[left-1]; }else { int max = Integer.MIN_VALUE; for(int i = left; i <= right; i++) { max = Math.max(max,nums[i]); } ans[left] = max; } left++; right++; } return ans; }}第五题: 剑指 Offer 59 - II. 队列的最大值
LeetCode: 剑指 Offer 59 - II. 队列的最大值
描述:
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1

解题思路:
这题思路是使用一个队列, 添加元素. 使用一个双端队列, 进行对最大值的添加在入队的时候, 判断当前双端队列是否为空, 不为空要进行比较 如果插入的value 要大于队尾元素, 就弹出队尾元素, 直到小于队尾元素, 或者队为空这个双端队列中始终放的是目前队列的最大值. 出队的时候, 如果为空直接返回-1, 如果不为空. 比较队列和双端队列的队首值,是否一直, 如果不一致, 表示目前最大值还没有出队, 不用管. 此时只用出队首元素, 不需要出双端队列队首元素.在得到最大值的时候, 如果队列为空就返回-1, 如果不为空, 直接返回双端队列的队首元素.代码实现:
class MaxQueue { private Queue<Integer> res; private Deque<Integer> tmp; public MaxQueue() { res = new LinkedList<>(); tmp = new LinkedList<>(); } public int max_value() { if(res.isEmpty()) { return -1; } return tmp.peekFirst(); } public void push_back(int value) { res.offer(value); while(!tmp.isEmpty() && value > tmp.peekLast()) { tmp.pollLast(); } tmp.offerLast(value); } public int pop_front() { if(res.isEmpty()) { return -1; } int val = res.poll(); if(val == tmp.peekFirst()){ tmp.pollFirst(); } return val; }}/** * Your MaxQueue object will be instantiated and called as such: * MaxQueue obj = new MaxQueue(); * int param_1 = obj.max_value(); * obj.push_back(value); * int param_3 = obj.pop_front(); */第六题: 剑指 Offer 60. n个骰子的点数
LeetCode: 剑指 Offer 60. n个骰子的点数
描述:
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

解题思路:
这里使用动态规划动态规划思路: 状态 F(i,j): 表示投了i个筛子, 点数为 j 的概率状态转移方程: F(i,j) = dp[i-1][j-k] * 1/6 (j>k)初始状态: F(1,j) = 1/6;返回结果: F代码实现:
class Solution { public double[] dicesProbability(int n) { // 点数j [1~6*n] double[][] dp = new double[n+1][6*n+1]; // 初始状态 for (int i = 1; i <= 6; i++) { dp[1][i] = 1/6.0; } for(int i = 2; i <= n; i++) { // j的范围[i,6i] for(int j = i; j <= 6*i; j++) { for(int k = 1; k <= 6; k++) { // 当 j > k 的时候,求的点数才有可能否者不可能丢出0 -1 if(j>k) { dp[i][j] += dp[i-1][j-k] * 1 / 6.0; }else{ // 只要这里 j<=k, 后面的情况只会更小, 直接跳过 break; } } } } // n个筛子,结果是[n,6n], 一共有, (6n-n)+1 = 5n+1个数 double[] res = new double[5*n+1]; for(int i = 0; i < 5 * n + 1; i++) { res[i] = dp[n][n+i]; } return res; }}第七题: 剑指 Offer 61. 扑克牌中的顺子
LeetCode: 剑指 Offer 61. 扑克牌中的顺子
描述:
从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。

解题思路:
本题的意思就是, 0可以当成别的牌这里首先进行排序.然后记录 zero 的次数zero记录完之后, 查看两个数组是否相差为1, 如果相差为1, 继续如果两个相等, 直接返回false;如果相差还有别的情况, 得到相差的牌数, 计算公式right - left -1, 根据这个数据, 查看zero是否足够, 如果zero<0 直接返回false. 遍历结束, 返回true 代码实现:
class Solution { public boolean isStraight(int[] nums) { Arrays.sort(nums); int zero = 0; int index = 0; for(int i = 0; i < nums.length - 1; i++) { if (nums[i] == 0) { zero++; }else{ if(nums[i] == nums[i+1]) { return false; } if(nums[i+1] - nums[i] != 1){ zero -= nums[i+1] - nums[i] - 1; if(zero < 0) return false; } } } return true; }}