特征选择、特征提取matlab算法实现(模式识别)
1、文档下载:
本算法已经整理成文档如下,有需要的朋友可以点击进行下载
| 序号 | 文档(点击下载) |
|---|---|
| 本项目文档 | 【老生谈算法】特征选择、特征提取matlab算法实现(模式识别).docx |
2、算法详解:
1 特征选择
1.1 问题
对“threethreelarge.m”数据,采用任意一种特征选择算法,选择2个特征
1.2 思路
采用简单特征选择法(simple feature selection approach),首先计算每一个特征的分类能力值,再选择出其中最大分类能力的l个特征。
1.3 结果
eigs = 8.9234 0.0000 0.0767
SelectedFeature = 1 3
也就是说,选取x和z坐标作为特征。
6.4 代码
% 特征选择代码,见FSthrthrlrg.m文件m1=[0,0,0]; m2=[0,0,0]; m3=[0,0,0]; m=[0,0,0];for i=1:200m1(1)=m1(1)+(x1(i,1)-m1(1))/i;m1(2)=m1(2)+(x1(i,2)-m1(2))/i;m1(3)=m1(3)+(x1(i,3)-m1(3))/i;end;for i=1:190m2(1)=m2(1)+(x2(i,1)-m2(1))/i;m2(2)=m2(2)+(x2(i,2)-m2(2))/i;m2(3)=m2(3)+(x2(i,3)-m2(3))/i;end;for i=1:210m3(1)=m3(1)+(x3(i,1)-m3(1))/i;m3(2)=m3(2)+(x3(i,2)-m3(2))/i;m3(3)=m3(3)+(x3(i,3)-m3(3))/i;end;m(1)=(m1(1)+m2(1)+m3(1))/3;m(2)=(m1(2)+m2(2)+m3(2))/3;m(3)=(m1(3)+m2(3)+m3(3))/3;sw1=zeros(3,3); sw2=zeros(3,3); sw3=zeros(3,3); sw=zeros(3,3); sb=zeros(3,3);for i=1:200sw1=sw1+([x1(i,1),x1(i,2),x1(i,3)]-m1)'*([x1(i,1),x1(i,2),x1(i,3)]-m1);end;for i=1:190sw2=sw2+([x2(i,1),x2(i,2),x2(i,3)]-m2)'*([x2(i,1),x2(i,2),x2(i,3)]-m2);end;for i=1:210sw3=sw3+([x3(i,1),x3(i,2),x3(i,3)]-m3)'*([x3(i,1),x3(i,2),x3(i,3)]-m3);end;N1=200; N2=190; N3=210; N=N1+N2+N3;p1=N1/N; p2=N2/N; p3=N3/N;sw1=sw1/N1; sw2=sw2/N2; sw3=sw3/N3;sw=p1*sw1+p2*sw2+p3*sw3;sb=p1*(m1-m)'*(m1-m)+p2*(m2-m)'*(m2-m)+p3*(m3-m)'*(m3-m);s=inv(sw)*sb;j1=trace(s)eigs=eig(s)'; eigsIndex=[1,2,3];% 冒泡法排序,注意的是特征值顺序变化的同时要与相对应的下标同步for i=1:3for j=i:3if(eigs(i)<eigs(j))eigstemp=eigs(i);eigs(i)=eigs(j);eigs(j)=eigstemp;eigsIndextemp=eigsIndex(i);eigsIndex(i)=eigsIndex(j);eigsIndex(j)=eigsIndextemp;end;end;end;% 降序排列后的特征值,直接选取前L个特征SelectedFeature=[eigsIndex(1),eigsIndex(2)]% FSthrthrlrg.m程序结束1.5 讨论
从实验结果中我们可以看到y特征的分类能力最小,这一点可以从实验数据中得到验证——三类数据在y方向的分布几乎是相同的(见下图)。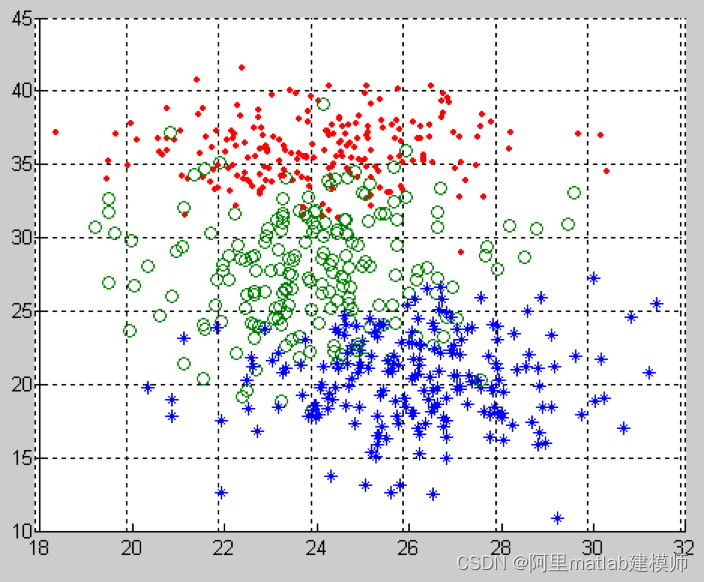
Threethreelarge:在y(横轴)方向上,三类数据几乎呈现一致的分布规律。
2 特征提取
2.1 问题
对“threethreelarge.m”数据,采用任意一种特征选择算法,选择2个特征
2.2 思路
采用简单特征选择法(simple feature selection approach),首先计算每一个特征的分类能力值,再选择出其中最大分类能力的l个特征。
2.3 结果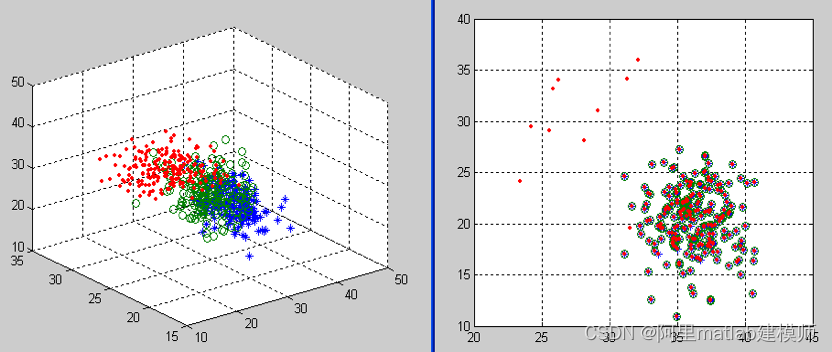
左图为Threethreelarge原始数据;右图将原始数据基于离差矩阵特征选择后进行的重构。
eigs = 8.9234 0.0000 0.0767
SelectedFeature = 1 3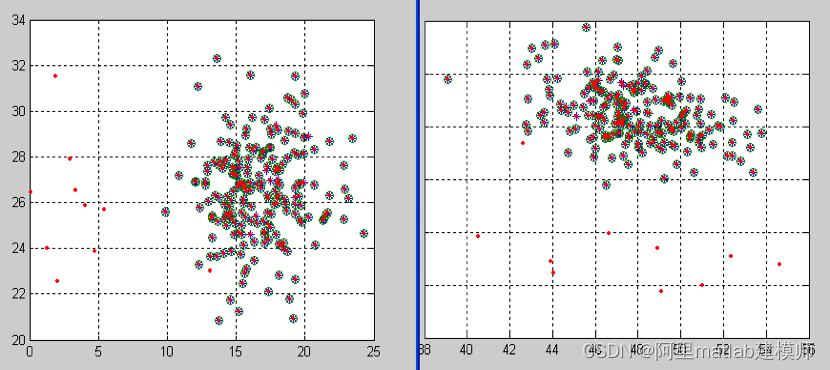
左图为基于离差矩阵进行特征提取后的重构数据;右图为基于自相关矩阵进行特征提取后的重构数据
eigRx = 1.0e+003 * 0.0057 0.0961 2.2111
SelF = 3 2
2.4 代码
% 特征提取代码,代码前半部分同特则选择代码(FSthrthrlrg.m),见FPthrthrlrg.m文件Yslc=zeros(600,2);for i=1:600Yslc(i,1)=xnew(i,SelectedFeature(1));Yslc(i,2)=xnew(i,SelectedFeature(2));end;for i=1:200 r16(i)=Yslc(i,1);end;for i=1:200 r17(i)=Yslc(i,2);end;for i=1:190 r18(i)=Yslc(i,1);end;for i=1:190 r19(i)=Yslc(i,2);end;for i=1:210 r20(i)=Yslc(i,1);end;for i=1:210 r21(i)=Yslc(i,2);end;figure(2);plot(r16,r17,'*',r18,r19,'o',r20,r21,'.');grid on;[eigV,eigD]=eig(s);A=[eigV(1,eigsIndex(1)),eigV(1,eigsIndex(2));eigV(2,eigsIndex(1)),eigV(2,eigsIndex(2));eigV(3,eigsIndex(1)),eigV(3,eigsIndex(2));];Ynew=zeros(600,2);for i=1:600Xktemp=[xnew(i,1);xnew(i,2);xnew(i,3)];Ytemp=A'*Xktemp;Ynew(i,1)=Ytemp(1,1); Ynew(i,2)=Ytemp(2,1);end;for i=1:200 r10(i)=Ynew(i,1);end;for i=1:200 r11(i)=Ynew(i,2);end;for i=1:190 r12(i)=Ynew(i,1);end;for i=1:190 r13(i)=Ynew(i,2);end;for i=1:210 r14(i)=Ynew(i,1);end;for i=1:210 r15(i)=Ynew(i,2);end;figure(3);plot(r10,r11,'*',r12,r13,'o',r14,r15,'.');grid on;Rx=zeros(3,3);for i=1:600Xk=[xnew(i,1),xnew(i,2),xnew(i,3)];Rx=Rx+Xk'*Xk;end;Rx=Rx/599;[eigRxv,eigRx]=eig(Rx);eigRx=eig(Rx)'eigRxIndex=[1,2,3];for i=1:3for j=i:3if(eigRx(i)<eigRx(j))eigRxtemp=eigRx(i);eigRx(i)=eigRx(j);eigRx(j)=eigRxtemp;eigRxIndextemp=eigRxIndex(i);eigRxIndex(i)=eigRxIndex(j);eigRxIndex(j)=eigRxIndextemp;end;end;end;SelF=[eigRxIndex(1),eigRxIndex(2)]ARx=[eigRxv(1,eigRxIndex(1)),eigRxv(1,eigRxIndex(2));eigRxv(2,eigRxIndex(1)),eigRxv(2,eigRxIndex(2));eigRxv(3,eigRxIndex(1)),eigRxv(3,eigRxIndex(2))];Ynew=zeros(600,2);for i=1:600Xktemp=[xnew(i,1);xnew(i,2);xnew(i,3)];Ytemp=ARx'*Xktemp;Ynew(i,1)=Ytemp(1,1); Ynew(i,2)=Ytemp(2,1);end;for i=1:200 r22(i)=Ynew(i,1);end;for i=1:200 r23(i)=Ynew(i,2);end;for i=1:190 r24(i)=Ynew(i,1);end;for i=1:190 r25(i)=Ynew(i,2);end;for i=1:210 r26(i)=Ynew(i,1);end;for i=1:210 r27(i)=Ynew(i,2);end;figure(4);plot(r22,r23,'*',r24,r25,'o',r26,r27,'.');grid on;%FPthrthrlrg.m程序结束2.5讨论
从实验结果可以看出,不论是进行特则选择还是基于自相关矩阵或者离差矩阵进行的特则提取最终得到的2维新数据分布都极其相似,说明了两点:
一 本问题给出的数据具有特殊性,离差矩阵有一个为0的特征值。
二 基于离差矩阵和自相关矩阵进行的特征变换本质上是相同的。