LeetCode 559 N叉树的最大深度[dfs bfs] HERODING的LeetCode之路_HERODING23的博客

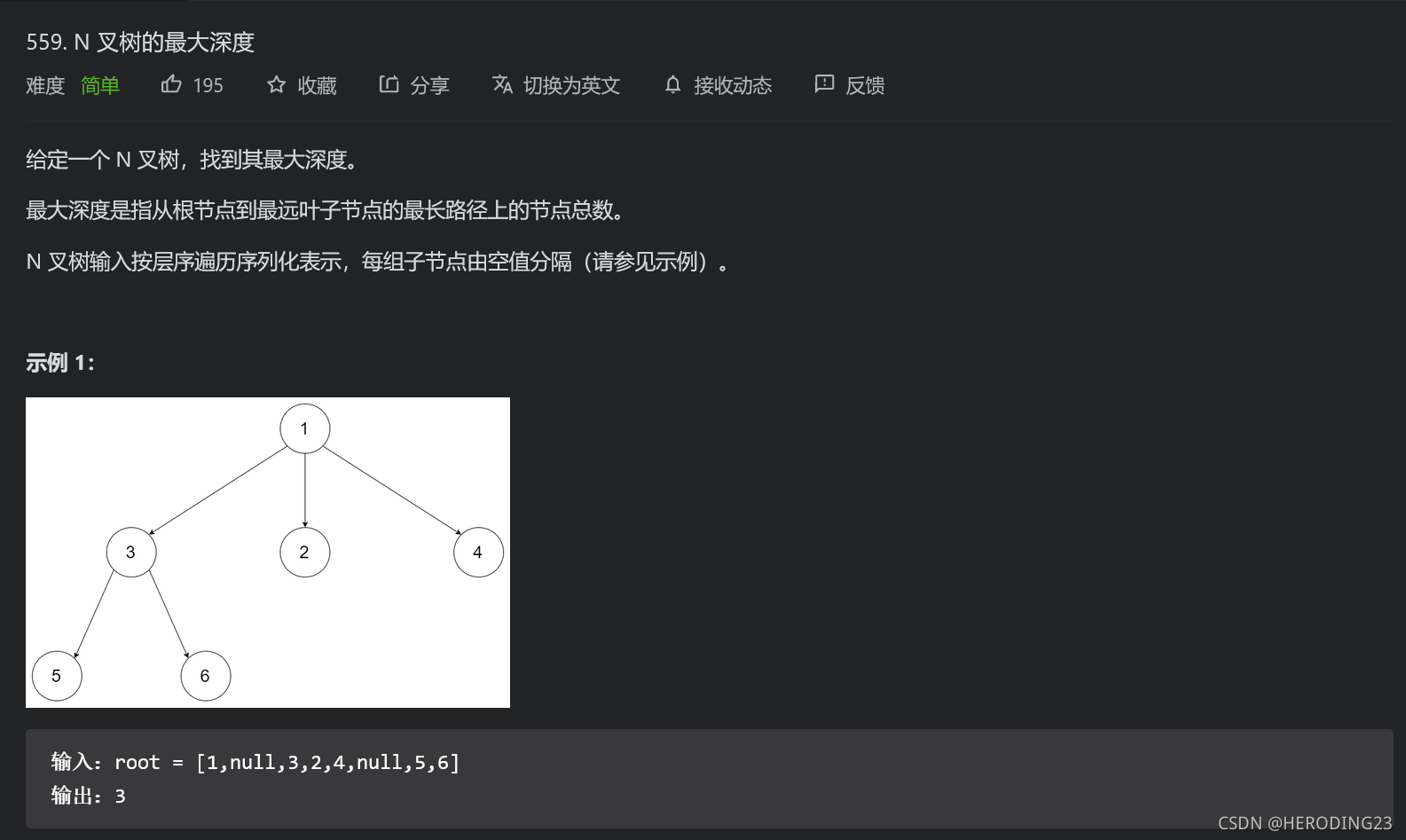
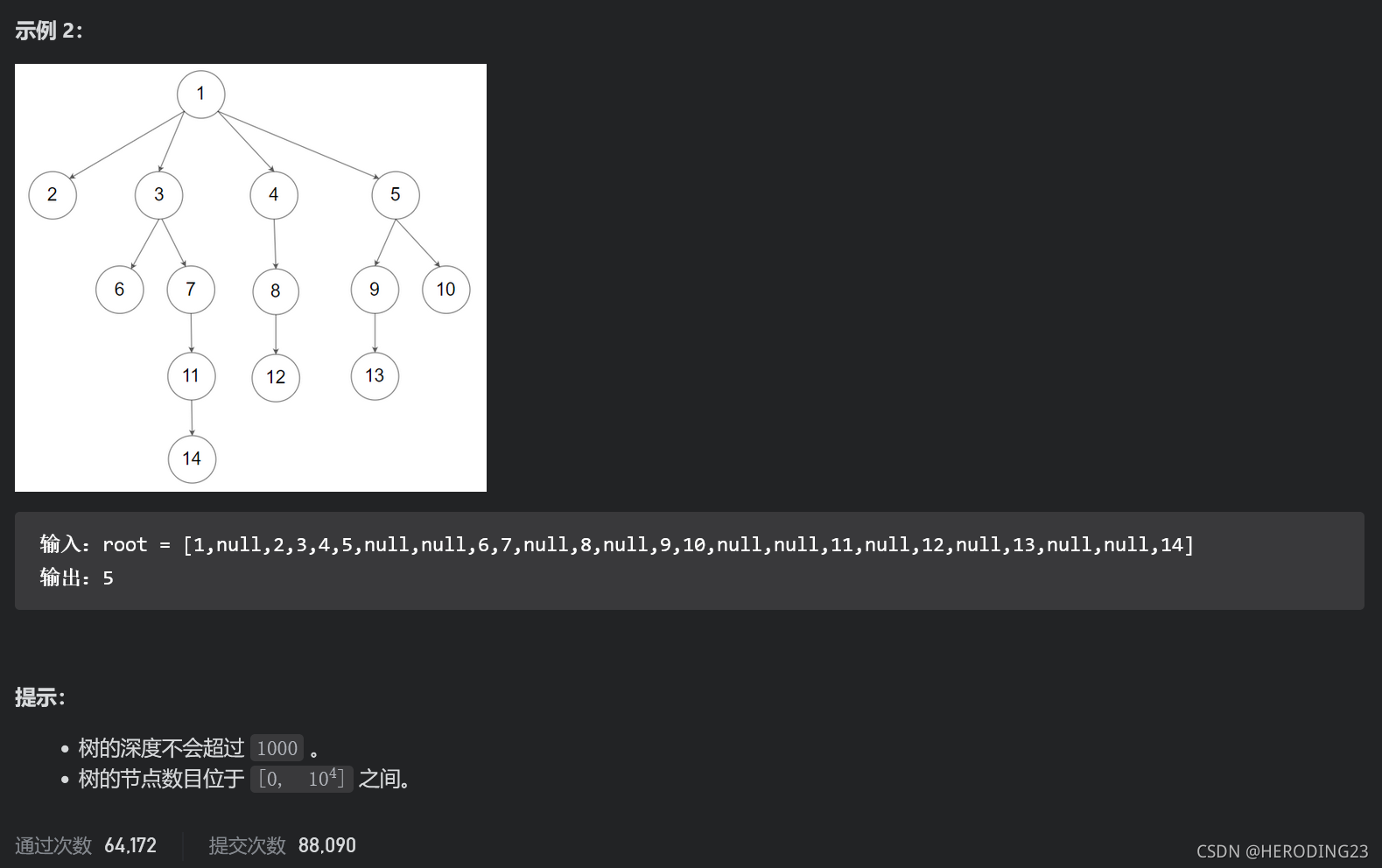
解题思路：
一道非常简单的搜索题目，无论是dfs还是bfs都可以轻松解决，对于dfs，首先定义变量depth作为最大深度，然后从每个节点搜下去，一直到最后一个节点（最后一个节点通过有没有孩子判断），然后更新最大深度，代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int depth = 0;
    int maxDepth(Node* root) {
        if(root == nullptr) {
            return 0;
        }
        dfs(root, 1);
        return depth;
    }

    void dfs(Node* root, int count) {
        if(root->children.size() == 0) {
            depth = max(depth, count);
            return;
        }
        for(auto child : root->children) {
            dfs(child, count + 1);
        }
    }
};

bfs的方法也是很简单，就是逐层遍历呗，不断放入队列中，直到队列中没有节点了，返回最大深度，代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if(root == nullptr) {
            return 0;
        }
        int depth = 0;
        queue<Node*> q;
        q.push(root);
        while(!q.empty()) {
            int len = q.size();
            for(int i = 0; i < len; i ++) {
                Node* node = q.front();
                q.pop();
                for(auto& child : node->children) {
                    q.push(child);
                }
            }
            depth ++;
        }
        return depth;
    }
};

最后再说一下这道题目本身，就是套用最简单的bfs和dfs的模板去写，没有一点难度，可以当做不是特别熟练这种类型题目的同学的入门题，也可以给那些老手练练手，所以这次两种方法我都写了，仅供大家参考。