最近公共祖先定义

查找最近公共祖先

三叉链

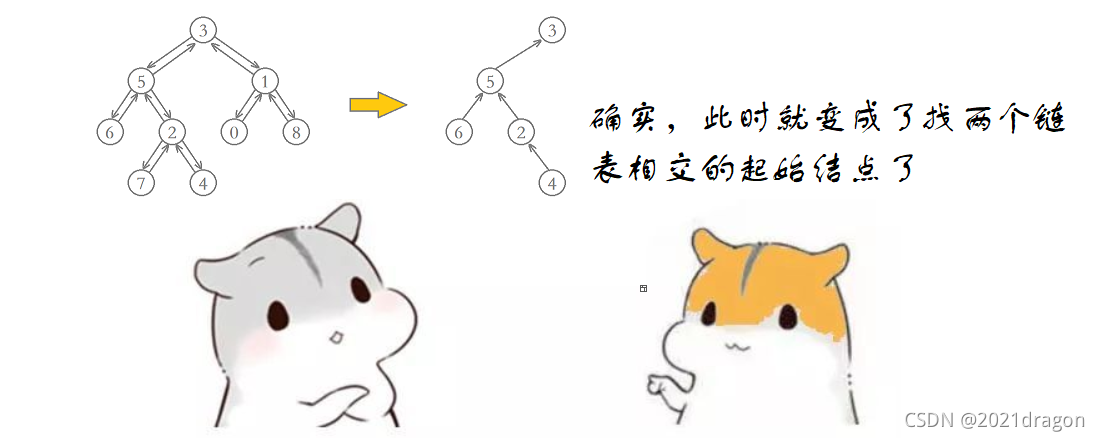
代码如下：

//三叉链
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
	TreeNode *parent;
    TreeNode(int x) : val(x), left(NULL), right(NULL), parent(NULL) {}
};
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		TreeNode* curp = p, *curq = q; //用于遍历p、q结点的祖先结点
		int lenp = 0, lenq = 0; //分别记录p、q结点各自的祖先结点个数
		//统计p结点的祖先结点个数
		while (curp != root)
		{
			lenp++;
			curp = curp->parent;
		}
		//统计q结点的祖先结点个数
		while (curq != root)
		{
			lenq++;
			curq = curq->parent;
		}
		//longpath和shortpath分别标记祖先路径较长和较短的结点
		TreeNode* longpath = p, *shortpath = q;
		if (lenp < lenq)
		{
			longpath = q;
			shortpath = p;
		}
		//p、q结点祖先结点个数的差值
		int count = abs(lenp - lenq);
		//先让longpath往上走count个结点
		while (count--)
		{
			longpath = longpath->parent;
		}
		//再让longpath和shortpath同时往上走，此时第一个相同的结点便是最近公共祖先结点
		while (longpath != shortpath)
		{
			longpath = longpath->parent;
			shortpath = shortpath->parent;
		}
		return longpath; //返回最近公共祖先结点
	}
};

二叉搜索树

代码如下：

//搜索二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		if (p->val == root->val || q->val == root->val) //p、q结点中某一个结点的值等于根结点的值，则根结点就是这两个结点的最近公共祖先
			return root;
		if (p->val < root->val&&q->val < root->val) //p、q结点的值都小于根结点的值，说明这两个结点的最近公共祖先在该树的左子树当中
			return lowestCommonAncestor(root->left, p, q);
		else if (p->val > root->val&&q->val > root->val) //p、q结点的值都大于根结点的值，说明这两个结点的最近公共祖先在该树的右子树当中
			return lowestCommonAncestor(root->right, p, q);
		else //p、q结点的值一个比根小一个比根大，说明根就是这两个结点的最近公共祖先
			return root;
	}
};

普通二叉树

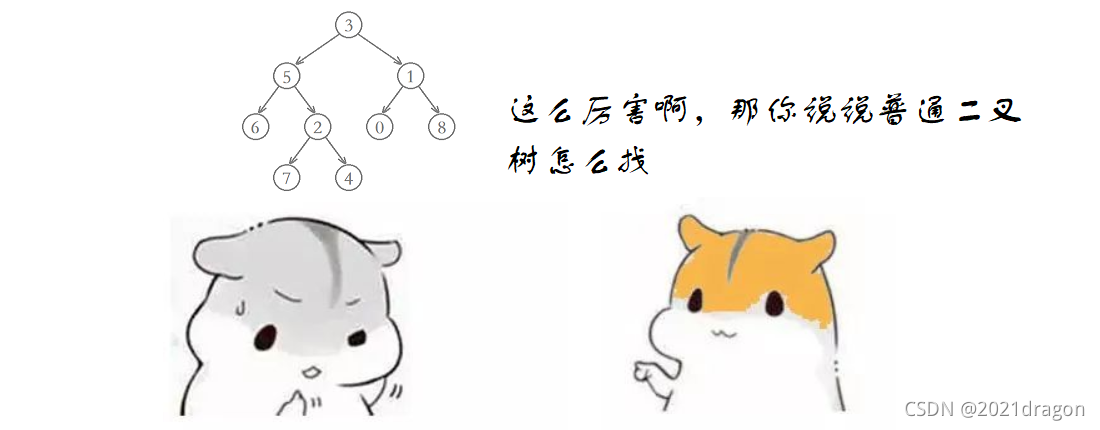
代码如下：

//普通二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	bool Find(TreeNode* root, TreeNode* x)
	{
		if (root == nullptr) //空树，查找失败
			return false;
		if (root == x) //查找成功
			return true;

		return Find(root->left, x) || Find(root->right, x); //在左子树找到了或是右子树找到了，都说明该结点在该树当中
	}
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		if (p == root || q == root) //p、q结点中某一个结点为根结点，则根结点就是这两个结点的最近公共祖先
			return root;
		//判断p、q结点是否在左右子树
		bool IspInLeft, IspInRight, IsqInLeft, IsqInRight;
		IspInLeft = Find(root->left, p);
		IspInRight = !IspInLeft;
		IsqInLeft = Find(root->left, q);
		IsqInRight = !IsqInLeft;

		if (IspInLeft&&IsqInLeft) //p、q结点都在左子树，说明这两个结点的最近公共祖先也在左子树当中
			return lowestCommonAncestor(root->left, p, q);
		else if (IspInRight&&IsqInRight) //p、q结点都在右子树，说明这两个结点的最近公共祖先也在右子树当中
			return lowestCommonAncestor(root->right, p, q);
		else //p、q结点一个在左子树一个在右子树，说明根就是这两个结点的最近公共祖先
			return root;
	}
};

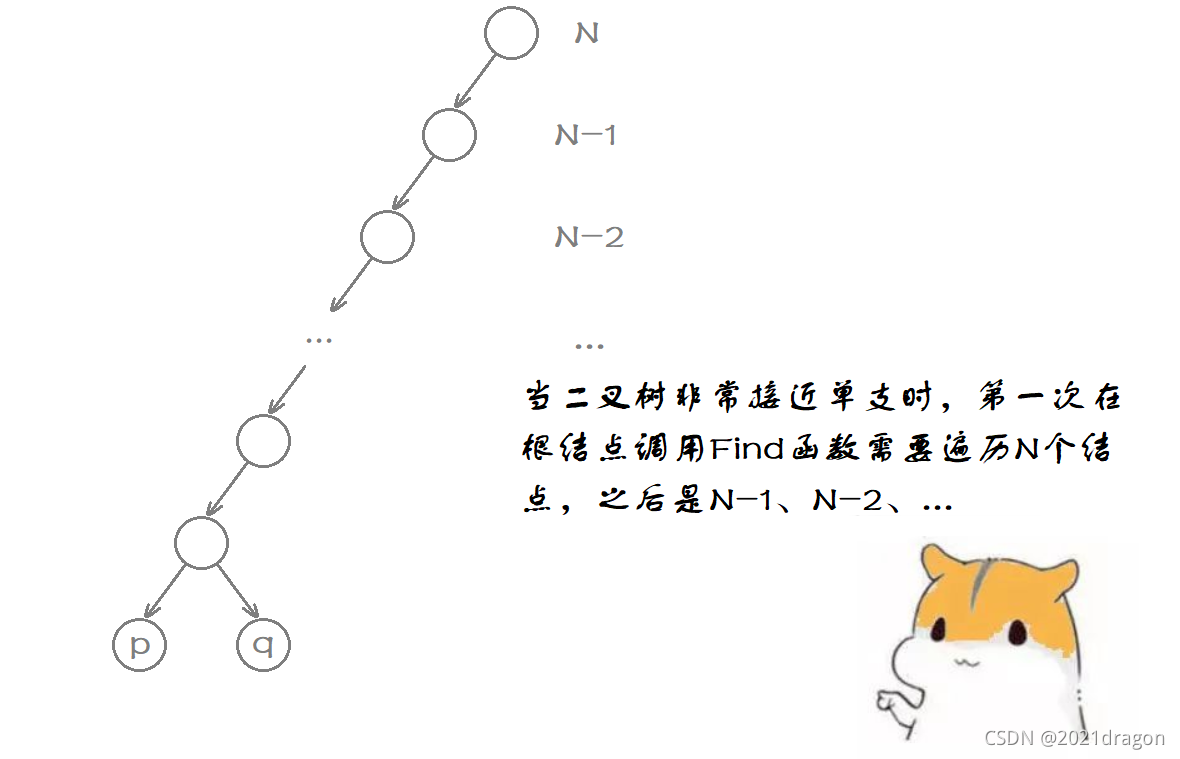
看着似乎不太好理解，来看看下面的动图演示：

代码如下：

//普通二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
	{
		if (root == nullptr)
			return false;
		path.push(root); //该结点可能是路径当中的结点，先入栈

		if (root == x) //该结点是最终结点，查找结束
			return true;

		if (FindPath(root->left, x, path)) //在该结点的左子树找到了最终结点，查找结束
			return true;
		if (FindPath(root->right, x, path)) //在该结点的右子树找到了最终结点，查找结束
			return true;

		path.pop(); //在该结点的左右子树均没有找到最终结点，该结点不可能是路径当中的结点，该结点出栈
		return false; //在该结点处查找失败
	}
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		stack<TreeNode*> pPath, qPath;
		FindPath(root, p, pPath); //将从根到p结点的路径存放到pPath当中
		FindPath(root, q, qPath); //将从根到q结点的路径存放到qPath当中
		//longpath和shortpath分别标记长路径和短路径
		stack<TreeNode*>* longPath = &pPath, *shortPath = &qPath;
		if (pPath.size() < qPath.size())
		{
			longPath = &qPath;
			shortPath = &pPath;
		}
		//让longPath先弹出差值个数据
		int count = longPath->size() - shortPath->size();
		while (count--)
		{
			longPath->pop();
		}
		//longPath和shortPath一起弹数据，直到两个栈顶的结点相同
		while (longPath->top() != shortPath->top())
		{
			longPath->pop();
			shortPath->pop();
		}
		return longPath->top(); //返回这个相同的结点，即最近公共祖先
	}
};