手把手教学考研大纲范围内树定义,遍历,Huffman,并查集
22考研大纲数据结构要求的是C/C++,笔者以前使用的都是Java,对于C++还很欠缺,
如有什么建议或者不足欢迎大佬评论区或者私信指出
初心是用最简单的语言描述数据结构
Talk is cheap. Show me the code.
理论到处都有,代码加例题自己练习才能真的学会
一、图的基本概念
图
官方解释:
图G由集合V和集合E组成,记作G = (V,E)
V(G)代表图G的顶点集合 (有穷非空集合)
E(G)代表图G的边集合(如果图G为空,则图只有顶点没有边)
歪理:
树是一个结点对应多个结点,图就是多个结点对应多个结点
图可以想象成一个乱七八糟的树
线性表和树都可以看作是一种特殊的图
图分为有向图和无向图
1、有向图:
顾名思义,有向图是有方向的图
1->2 但是 2不能指向1

2、无向图:
没有方向的图
只要有边存在就可以互相走,a -> c , c -> a 两种都存在
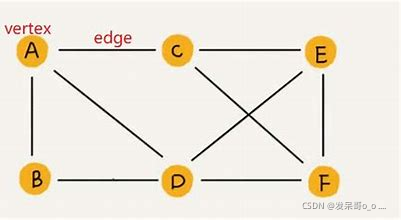
3、子图:
官方解释:
G = (V,E)和G' = (V', E')
V'属于V, E'属于E
称G'为G的子图
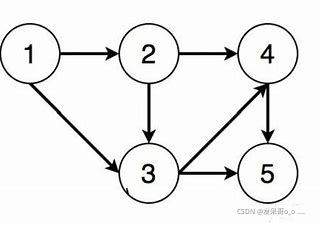
当前图的子图有:
1 -> 2
1 -> 2 -> 4
3 -> 4
等等很多,无向图也是一样的
4、完全图:
对于无向图:
若具有n(n-1)条边,则称为无向完全图。
对于有向图:
若具有n(n-1)条边,则称为有向完全图。
5、稀疏图和稠密图:
边的数量相对顶点很少的图称为稀疏图,反之称为稠密图。
6、权和网:
在一些情况下,每条边可以标上具有某种含义的数值,该数值称为该边上的权。
这些权表示从 一个顶点到另一个顶点 的距离或者耗费,这种带权的图通常称为网。
7、邻接点:
对于无向图G,如果图的边(a,b)属于 E ,则称 a,b 互为邻接点,即 a,b 相邻接,边(a,b)依附于顶点 a 和 b ,边(a,b)与顶点a,b相关联。
8、度,入度和出度:
顶点 v 的度是:与 v 相关联的边的数目,记作 TD(v) 。
对于有向图,顶点 v 的度分为入度和出度:
入度是指向 v 的边的数目,记为 ID(v) 。
出度是从 v 指出来的边的数目,记作 OD(v) 。
例子:

以顶点 2 为例子:
顶点 2 的入度ID(v)= 1
顶点 2 的出度OD(v)= 2
顶点 2 的度为TD(v)= ID(v)+ OD(v)= 3
边和度之间的关系:
顶点 vi 的度记为 TD(v),那么一个有 n 个顶点,e 条边的图,满足如下关系
e = (TD(v1) + TD(v2) + …… +TD(vn))/ 2
7、路径和路径长度:
顶点 Va 到顶点 Vb 之间的 路径: 是指顶点序列 {Va,Vi1,Vi2,……,Vim,Vb}
路径长度: 路径中边的数目
回路或环: 第一个顶点和最后一个顶点 相同的路径 称为回路或环(也就是 a 和 b 相同)
简单路径: 路径中顶点不重复出现的路径的路径为简单路径
简单回路 或 简单环: 除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路 或 简单环
8、连通、连通图和连通分量:
在无向图中
如果从顶点 A 到顶点 B 有路径,则称 A 和 B 是 连通 的
如果图中任意两个两个顶点 A ,B 都是连通的,则称图为 连通图
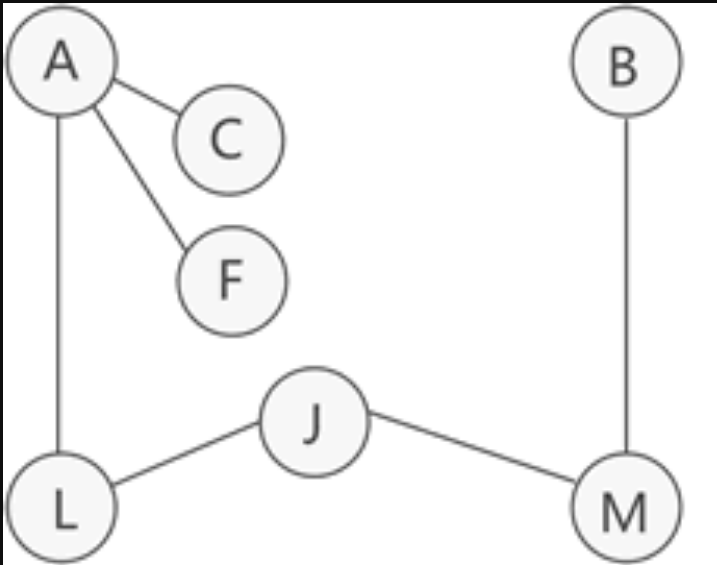
在无向图中
上图不是连通图
下面是上图的三个连通分量
连通分量也称作无向图中的极大连通子图
也就是说,把一个非连通图完全分成多个连通图,这些连通图就叫做连通分量
9、强连通图和强连通分量:
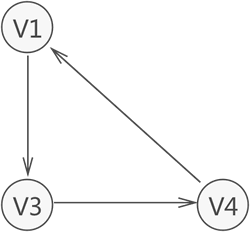
在有向图中 如果图中任意两个两个顶点 A ,B 都是连通的,则称图为 强连通图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-75x2Ch0D-1637418026290)(https://tse1-mm.cn.bing.net/th/id/R-C.df6e4aa9b6d0910b9adb742d1e2bf7ab?rik=gV5%2bFlnZ8HdsVg&riu=http%3a%2f%2fupload-images.jianshu.io%2fupload_images%2f2015908-8d71b80d28821271.png%3fimageMogr2%2fauto-orient%2fstrip%7cimageView2%2f2%2fw%2f1240&ehk=u2cPVkXWyBkCCBqel5lxota5Wb2M3v%2fIwQ8YVU8cg9U%3d&risl=&pid=ImgRaw&r=0)]
在有向图中: G4不是强连通图,但是他有三个强连通分量
10、连通图的生成树、有向树和生成森林:
**连通图的生成树:**是包含图中全部顶点的一个极小连通子图。若图中顶点数为 n ,则它的生成树含有 n − 1 条边。
对生成树而言,若砍去一条边,则会变成非连通图
若加上一条边则会形成一个回路。
在非连通图中,连通分量的生成树构成了非连通图的生成森林
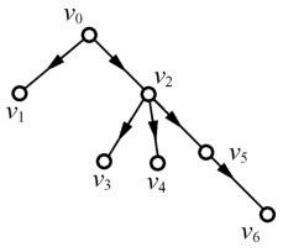
有向树: 有一个顶点的入度为0,其余顶点的入度均为1的有向图称为有向树
换句话说,一个有向图的生成森林是由若干棵有向树组成。
二、图的存储结构
图的结构相对于其他来说比较复杂,任何两个顶点之间都可能存在联系,无法用顺序存储的方式存储图之间的关系(无法用一维数组来保存图)
虽然图无法用顺序存储的方式,但是可以用二维数组的方式表示元素之间的关系,即 邻接矩阵 表示法。
由于图的任意两个结点都可能存在关系,用链式存储图也很常见。
图的链式存储有:邻接表、十字链表和邻接多重表。(应该根据实际需要选择不通的存储结构)
2.1、邻接矩阵
邻接矩阵: 顶点之间相邻关系的矩阵。
图
图G(V,E)是具有 n 个顶点的图(A[ i,j] = 1表示顶点 i 和顶点 j 有一条边联系,反之则没有边联系)

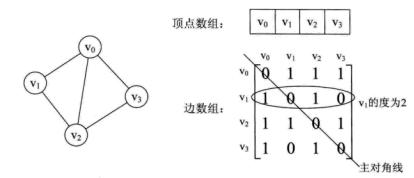
**对角线上的都是0:**都是对应当前点(V0,V0 V1,V1 ……)顶点是无法自身与自身相连接的
对于无向图来说,其实他们是关于对角线对称的( i 与j相连,那么j与i肯定也是相连的)
对于有向图来说,没有这个规律 ( i 与j相连,那么j与i不一定相连)
网
网G,邻接矩阵可以定义为如下(其实和图是一样的,不过就是把顶点有关系变成了顶点直接的权值)
A[ i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3

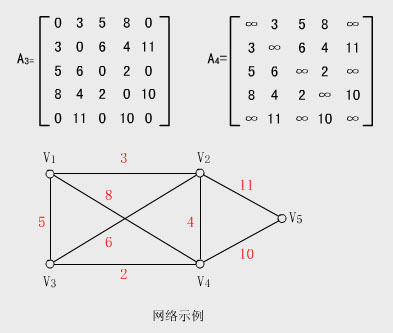
和图一样,对角线上一定为0,顶点无法与自身相连接
邻接矩阵示例代码
代码:
(无向图也可以这么创建,无向图就不需要输入权值了,把相关联的两个点在矩阵中置1)
#include <iostream>
using namespace std;
#define None 0 //顶点之间没有关系用0表示
#define MAXNum 100 //设图中顶点数量最多为100
typedef struct { //图的结构体:顶点列表,邻接矩阵,图的点数和边数
int nodes[MAXNum];
int arcs[MAXNum][MAXNum];
int vewnum, arcnum;
} AMGraph;
//取顶点在顶点表中的下标
int getAMGraphIndex(AMGraph G, int node) {
for (int i = 0; i < G.vewnum; i++) { //循环顶点表,找到顶点,返回下标
if (G.nodes[i] == node) {
return i;
}
}
return -1;
}
//邻接矩阵法创建无向图
bool createAMGraph (AMGraph &G) {
cout << "请输入顶点数量和边的数量" << endl;
cin >> G.vewnum >> G.arcnum; //输入 顶点数 和 边数
for (int i = 0; i < G.vewnum; i++) { //输入顶点
cout << "请输入顶点的值" << endl;
cin >> G.nodes[i];
}
for (int i = 0; i < G.vewnum; i++) { //邻接矩阵,初始化顶点间的边(关系)都为空
for (int j = 0; j < G.vewnum; j++) {
G.arcs[i][j] = None;
}
}
int v1, v2, w;
int i1, i2;
for (int i = 0; i < G.arcnum; i++) { //接收两个顶点和顶点间边的权值
cout << "请输入新建边相邻的两个结点,以及这条边的权重" << endl;
cin >> v1 >> v2 >> w;
i1 = getAMGraphIndex(G, v1); //找到两个顶点的下标
i2 = getAMGraphIndex(G, v2);
G.arcs[i1][i2] = G.arcs[i2][i1] = w; //在邻接矩阵中建立关系
}
return true;
}
//输出图
void printAMGraph(AMGraph G) {
cout << "顶点数:" << G.vewnum << "边数:" << G.arcnum << "\n";
cout << "顶点表:";
for (int i = 0; i < G.vewnum; i++) {
cout << G.nodes[i] << " ";
}
cout << "\n";
cout << "邻接矩阵关系(A[i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3):\n";
for (int i = 0; i < G.vewnum; i++) {
for (int j = 0; j < G.vewnum; j++) {
cout << G.arcs[i][j] << " ";
}
cout << "\n";
}
cout << "\n";
}
int main() {
AMGraph G;
//输入例子
//5 6 1 2 3 4 5 1 5 8 1 3 6 1 4 9 2 3 8 5 4 9 3 4 6
createAMGraph(G);
printAMGraph(G);
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量和边的数量
5 6
请输入顶点的值
1
请输入顶点的值
2
请输入顶点的值
3
请输入顶点的值
4
请输入顶点的值
5
请输入新建边相邻的两个结点,以及这条边的权重
1 5 8
请输入新建边相邻的两个结点,以及这条边的权重
1 3 6
请输入新建边相邻的两个结点,以及这条边的权重
1 4 9
请输入新建边相邻的两个结点,以及这条边的权重
2 3 8
请输入新建边相邻的两个结点,以及这条边的权重
5 4 9
请输入新建边相邻的两个结点,以及这条边的权重
3 4 6
顶点数:5边数:6
顶点表:1 2 3 4 5
邻接矩阵关系(A[i,j] = 3 表示顶点 i 和顶点 j 有一条边,边的权值为3):
0 0 6 9 8
0 0 8 0 0
6 8 0 6 0
9 0 6 0 9
8 0 0 9 0
Process finished with exit code 0
2.2、邻接表
当一个图中,边的数量少 时(也叫做稀疏图),用邻接矩阵会很 浪费空间 ,这时候 邻接表 就出来了
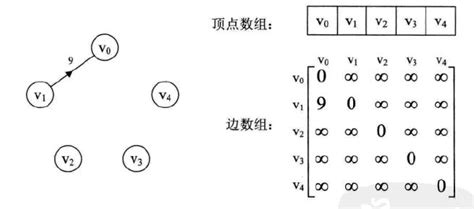
邻接表结构:
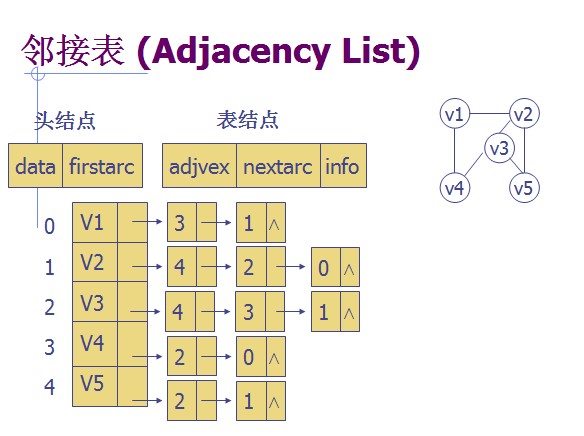
头结点包含一个 顶点 和一个指向 边(表结点) 的指针
表结点包含一个 顶点 ,一个指向 下一条边(表结点) 的指针 和 边的权值(图没有权值)
Tips: 这里指向的边,都是 以当前 头结点 顶点 直接联系 的边
eg:
比如这个以 V1 直接联系的点是 V4 和 V2 ,所以表结点是 V4 和 V2
无向图
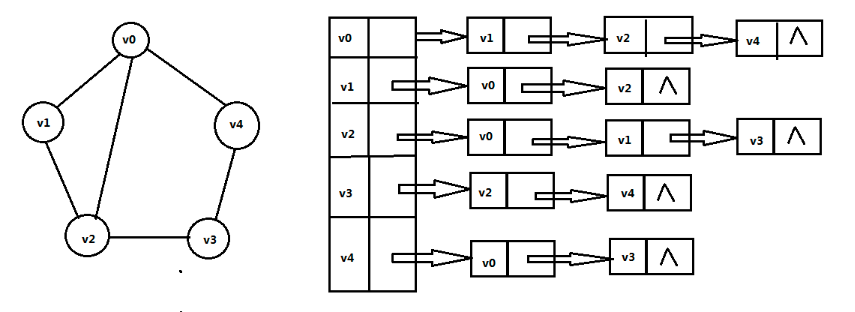
有向图
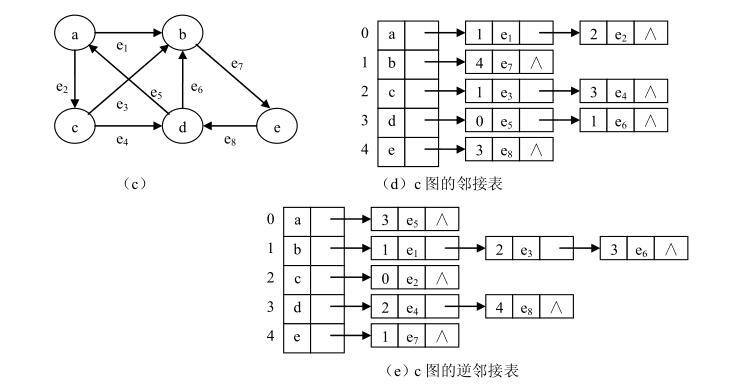
解释:
0-4 代表 a-e
邻接矩阵中,是以顶点为起点的关系(逆邻接矩阵,以顶点为终点的关系)
0 -> 1 (a->b) 的边,权重 e1
0 -> 2 (a->c) 的边,权重 e2
0没有指向其他方向的边了
多分析分析这几个图,其实很容易懂得
邻接表示例代码
代码:
#include "iostream"
using namespace std;
#define MAXNum 100 //顶点数最大为100
typedef struct ArcNode { //定义边结点结构体:顶点的邻点adjvex,边的权重,下一个边结点的指针
int adjvex;
int info;
struct ArcNode *nextarc;
} ArcNode;
typedef struct VNode { //定义表头结点结构体:顶点data,指向边结点的指针
int data;
ArcNode *firstarc;
} VNode, AdjList[MAXNum]; //AdjList 是表头结点的数组类型
typedef struct { //定义邻接表结构体:表头结点数组,顶点数量和边数量
AdjList vertices;
int vexnum, arcnum;
} ALGraph;
//找到顶点在表头结点的下标
int getGraphIndex(ALGraph G, int targetnode) {
for (int i = 0; i < G.vexnum; i++) {
if (G.vertices[i].data == targetnode) {
return i;
}
}
return -1;
}
//创建邻接表
bool createGraph(ALGraph &G) {
cout << "请输入顶点数量和边的数量" << endl;
cin >> G.vexnum >> G.arcnum; //输出顶点数量和边数量
for (int i = 0; i < G.vexnum; i++) { //输出顶点,并且设置指向的边结点为空
cout << "请输入顶点的值" << endl;
cin >> G.vertices[i].data;
G.vertices[i].firstarc = NULL;
}
int v1, v2, i1, i2;
for (int i = 0; i < G.arcnum; i++) { //输入两个相邻的顶点
cout << "请输入新建边相邻的两个结点" << endl;
cin >> v1 >> v2;
i1 = getGraphIndex(G, v1); //找到两个顶点的下标
i2 = getGraphIndex(G, v2);
ArcNode *p1 = new ArcNode; //创建p1边结点,让v1表头结点指向p1边结点
p1->adjvex = v2; //p1设置邻接点为v2
p1->nextarc = G.vertices[i1].firstarc; //采用头插法,如果采用尾插,每次都要循环到当前表头结点的最后一个末尾边结点才能插入
G.vertices[i1].firstarc = p1;
ArcNode *p2 = new ArcNode; //与上面同理
p2->adjvex = v1;
p2->nextarc = G.vertices[i2].firstarc;
G.vertices[i2].firstarc = p2;
}
return true;
}
//输出邻接表
void printGraph(ALGraph G) {
for (int i = 0; i < G.vexnum; i++) {
cout << G.vertices[i].data << " : ";
ArcNode *temp = G.vertices[i].firstarc;
while (temp != NULL) {
cout << "下一个顶点:" << temp->adjvex << " ";
temp = temp->nextarc;
}
cout << "下一个顶点为空\n";
}
}
int main() {
ALGraph G;
//输入样例:4 3 1 2 3 4 1 2 1 3 2 3
createGraph(G);
printGraph(G);
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量和边的数量
4 3
请输入顶点的值
1
请输入顶点的值
2
请输入顶点的值
3
请输入顶点的值
4
请输入新建边相邻的两个结点
1 2
请输入新建边相邻的两个结点
1 3
请输入新建边相邻的两个结点
2 3
1 : 下一个顶点:3 下一个顶点:2 下一个顶点为空
2 : 下一个顶点:3 下一个顶点:1 下一个顶点为空
3 : 下一个顶点:2 下一个顶点:1 下一个顶点为空
4 : 下一个顶点为空
Process finished with exit code 0
2.3、十字链表
十字链表特点:
十字链表是有向图的另一种链式结构,可以看作邻接表和逆邻接表结合起来得到的一种链表。
十字链表可以快速得到与某点相关联的边,可以高效存取。
大致理解为:每一行第一个为顶点结点,顶点结点的指针根据规律指向对应的边结点。
十字链表结构:

顶点表结点:
data:表示顶点的值
firstin:指向第一个以当前结点为终止点的边(first 第一个 in 进入 第一个进入该结点的边)
firstout:指向第一个以当前结点为起始点的边(first 第一个 out 出去 第一个从该结点出去的边)
边结点:
tailvex:存储边的起始点。(tailvex代表的是弧尾,也就是起始点 A -> B 弧尾是A,这条边从A开始)
headvex:存储边的终止点(headvex 代表的是弧头)
hlink:指向上一条以 headvex 为终止点的边。
tlink:指向上一条以 tailvex 为起始点的边。
十字链表例图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0Q0QFhY0-1637418026309)(https://tse1-mm.cn.bing.net/th/id/R-C.a10051fc3c5919b3a3e16936e4f38f90?rik=p9TqaLD3G%2f1cfQ&riu=http%3a%2f%2fdata.biancheng.net%2fuploads%2fallimg%2f190107%2f2-1Z10H11122456.gif&ehk=%2ffw8m0g04yWye0qjikwIzKthZfijC%2bAo0j0TBpva6Rw%3d&risl=&pid=ImgRaw&r=0)]
以 V1 点为例子,
找从V1起始的边:
V1的 firstout(指向第一个以当前结点为起始点的边)指向边 0->1 ,(这里存储的是结点下标)
此边的 tlink (指向和当前边的起始结点相同的上一条边)指向 0->2
可一直通过边的 tlink 找到相同起始点的边
找以 V1 结束的边:
V1 的 firstin (指向第一个以当前结点为终止点的边)指向边 3->0 ,
此边的 hlink (指向和当前边终止结点相同的上一条边) ,不存在终止结点相同上一条边,此时为NULL
可一直通过边的 hlink 找相同终止点的边
十字链表的最大优点:
把邻接表和逆邻接表整合在一起了,很容易找到以 V1 为起始点的边,也容易找到以 V1 为终止点的边。
十字链表示例代码
代码:
#include "iostream"
using namespace std;
#define MAXSize 100 //顶点数最大为100
typedef struct ArcNode { //定义边结点结构体:(边采用头插法)
int info; //边的权重,
int tailvex; //边的尾结点的下标(一条边的起始点下标)
int headvex; //边的头结点的下标(一条边的终止点下标)
struct ArcNode *hlink; //指向上一条 与边的头结点相同的边 (指向上一条有相同起始点的边)
struct ArcNode *tlink; //指向上一条 与边的尾结点相同的边 (指向上一条有相同终止点的边)
} ArcNode;
typedef struct VNode { //定义表头结点结构体:
int data; //结点的数据
ArcNode *firstin; //指向最后一条以当前顶点为结尾的边(最后一条以当前点的下标为终止点的边)
ArcNode *firstout; //指向最后一条以当前顶点为起始的边(最后一条以当前点的下标为起始点的边)
} VexNode;
typedef struct { //定义十字链表结构体:表头结点数组,结点数量和边数量
VexNode vexlist[MAXSize];
int vexnum, arcnum;
} ALGraph;
//找到顶点在表头结点的下标
int getGraphIndex(ALGraph G, int targetnode) { //通过结点的值,找到在图中表头结点的下标(如果不存在,返回-1)
for (int i = 0; i < G.vexnum; i++) {
if (G.vexlist[i].data == targetnode) {
return i;
}
}
return -1;
}
//创建边
bool createArc(ALGraph &G) { //(边采用头插法)
int vex1, vex2, index1, index2; //起始点,终止点,起始点下标,终止点下标
cout << "输入边的起始点和终止点" << endl;
cin >> vex1 >> vex2;
index1 = getGraphIndex(G, vex1); //找到两个顶点的下标
index2 = getGraphIndex(G, vex2);
if (index1 == -1 && index2 == -1) {
cout << "起始顶点和终止顶点不存在" << endl;
return false;
} else if (index1 == -1) {
cout << "起始顶点不存在" << endl;
return false;
} else if (index2 == -1) {
cout << "终止顶点不存在" << endl;
return false;
}
ArcNode *newArc = new ArcNode; //创建新边结点,新边的起始点指向index1,终止点指向index2
newArc->tailvex = index1;
newArc->headvex = index2;
ArcNode *oldtail = G.vexlist[index1].firstout; //找到当前index1为起始点的第一条边
ArcNode *oldhead = G.vexlist[index2].firstin; //找到当前index2为终止点的第一条边
newArc->hlink = oldhead; //新边的index2为终止点的边指向oldhead(oldhead就成了上一个以index2为终止点的边)
newArc->tlink = oldtail; //新边的index2为起始点的边指向oldtail(oldtail就成了上一个以index2为起始点的边)
G.vexlist[index1].firstout = newArc; //以index1为起始点的第一条边指向新边(头插法)
G.vexlist[index2].firstin = newArc; //以index2为终止点的第一条边指向新边
cout << vex1 << "->" << vex2 << " 创建成功" << endl;
return true;
}
//删除边
bool deleteArc(ALGraph &G) {
int vex1, vex2, index1, index2;
cout << "输入边的起始点和终止点" << endl;
cin >> vex1 >> vex2;
index1 = getGraphIndex(G, vex1);
index2 = getGraphIndex(G, vex2);
if (index1 == -1 && index2 == -1) {
cout << "起始顶点和终止顶点不存在" << endl;
return false;
} else if (index1 == -1) {
cout << "起始顶点不存在" << endl;
return false;
} else if (index2 == -1) {
cout << "终止顶点不存在" << endl;
return false;
}
ArcNode *targetArc;
ArcNode *firstOutCur = G.vexlist[index1].firstout; //找到index1为起始点的第一条边
ArcNode *firstOutPre;
int count = 0;
while (firstOutCur) { //看边是否存在
count++; //每循环一次就是上一条边,count每次加1,记录这是第几条边
//找到起始点和终止点对应的那条边(找到就终止)
if (firstOutCur->tailvex == index1 && firstOutCur->headvex == index2) {
break;
}
firstOutPre = firstOutCur; //把当前边给pre,cur指向下一个以index1为起始点的边
firstOutCur = firstOutCur->tlink;
}
if (count == 0 || !firstOutCur) { //count等于0 说明没进循环 firstOutCur为空
cout << "不存在该边" << endl; //或者 找了所有以index1为起始点的边没有找到这条边
return false;
} else if (count == 1) { //如果count=1 说明循环了一次就找到了这条边,这是第一条边
//就把以index1为起始点的第一条边指向这条边的下一个,把这条边以index1为起始点的关系解除
G.vexlist[index1].firstout = firstOutCur->tlink;
} else {
//把这条边的上一条边的相同起始点的边 指向 这条边下一条相同起始点的边,把这条边以index1为起始点的关系解除
firstOutPre->tlink = firstOutCur->tlink;
}
targetArc = firstOutCur; //只要没有返回false,证明当前存在这条边
//下面的是找以index2为终止点的边 与上面大概类似!!!
count = 0; //count重置为0
ArcNode *firstInCur = G.vexlist[index2].firstin;
ArcNode *firstInPre;
while (firstInCur) { //如果以index2为终止点的边不为空,一直循环
count++; //每次循环,都是一条新边, count+1
if (firstInCur==targetArc) { //如果当前边是上面找出来的那条边,终止循环
break;
}
firstInPre = firstInCur; //当前边保存到pre,当前边继续找index2为终止点的边
firstInCur = firstInCur->hlink;
}
if (count == 0 || !firstOutCur) {
cout << "不存在该边" << endl;
return false;
} else if (count == 1) {
G.vexlist[index2].firstin = firstInCur->hlink;
} else {
firstInPre->hlink = firstInCur->hlink;
}
G.arcnum--; //删除后图的边数-1
cout << vex1 << "->" << vex2 << " 删除成功" << endl;
return true;
}
//根据下标删除边(删除结点时使用) //删除结点的时候使用此方法,因为要频繁的删除与结点相关的边
bool deleteArc(ALGraph &G, int index1, int index2) { //方法和上面删除边的方法基本类似,这里的下标是不需要输入的
ArcNode *firstOutCur = G.vexlist[index1].firstout;
ArcNode *firstOutPre;
int count = 0;
while (firstOutCur) {
count++;
if (firstOutCur->tailvex == index1 && firstOutCur->headvex == index2) {
break;
}
firstOutPre = firstOutCur;
firstOutCur = firstOutCur->tlink;
}
if (count == 0 || !firstOutCur) {
return false;
} else if (count == 1) {
G.vexlist[index1].firstout = firstOutCur->tlink;
} else {
firstOutPre->tlink = firstOutCur->tlink;
}
count = 0;
ArcNode *firstInCur = G.vexlist[index2].firstin;
ArcNode *firstInPre;
while (firstInCur) {
count++; //这里可以用下标匹配删除,如果存在多条起点和终点相同的边(平行边),删除的一定是相同一条边!!!
//插入边的时候采用的是头插法,最后插入的边一定在最后,
// 搜起始点相同的也是先搜到的最后一个边,终止点相同的也是最后一个边
if (firstInCur->tailvex == index1 && firstInCur->headvex == index2) {
break;
}
firstInPre = firstInCur;
firstInCur = firstInCur->hlink;
}
if (count == 0 || !firstOutCur) {
return false;
} else if (count == 1) {
G.vexlist[index2].firstin = firstInCur->hlink;
} else {
firstInPre->hlink = firstInCur->hlink;
}
G.arcnum--;
return true;
}
//删除结点
bool deleteVex(ALGraph &G) {
cout << "请输入删除的顶点" << endl;
int vex, index;
cin >> vex;
index = getGraphIndex(G, vex);
for (int i = 0; i < G.vexnum; ++i) { //循环每一个顶点,删除与他相关的边
while (deleteArc(G, index, i));//删除下标 index->i 的边,
// 如果删除成功返回true,继续循环,防止有平行边,当删除失败说明不存在边,返回false
while(deleteArc(G, i, index)); //同上 删除 i->index 的边
}
G.vexlist[index].data = -1; //删除完结点,设置此结点的值为-1,表示结点已删除
cout << "结点已删除" << endl;
}
//添加结点
bool createVex(ALGraph &G) {
cout << "请输入添加结点的值" << endl;
int data;
cin >> data;
G.vexlist[G.vexnum].data = data; //设置结点的数值,以该结点为终止点,以该结点为初始点的边赋值空
G.vexlist[G.vexnum].firstin = NULL;
G.vexlist[G.vexnum].firstout = NULL;
G.vexnum++;
cout << "添加结点成功" << endl;
}
//创建十字链表
bool createGraph(ALGraph &G) {
G.vexnum = 0; //图的初始结点数量为0
cout << "请输入顶点数量" << endl;
int count;
cin >> count; //输出顶点数量和边数量
for (int i = 0; i < count; i++) { //循环创建count个结点
createVex(G);
}
cout << "请输入边的数量" << endl;
cin >> G.arcnum;
int v1, v2;
for (int i = 0; i < G.arcnum; i++) { //循环创建边
createArc(G);
}
cout << "初始化十字链表成功" << endl;
return true;
}
//打印十字链表
void printGraph(ALGraph G) {
cout <<endl;
for (int i = 0; i < G.vexnum; i++) {
if (G.vexlist[i].data == -1) { //如果该结点的值为 -1 说明该结点被删除了,跳过本次循环
continue;
}
ArcNode *tail = G.vexlist[i].firstout; //找到第一条以该结点为初始点的边
ArcNode *head = G.vexlist[i].firstin; //找到第一条以该结点为终止点的边
cout << G.vexlist[i].data << " 起始的边有: ";
while (tail) { //输出完当前边的信息,接着找上一条以当前点为初始点的边
cout << G.vexlist[tail->tailvex].data << "->" << G.vexlist[tail->headvex].data << " ";
tail = tail->tlink;
}
cout << endl << G.vexlist[i].data << " 结束的边有: ";
while (head) { //输出完当前边的信息,接着找上一条以当前点为终止点的边
cout << G.vexlist[head->tailvex].data << "->" << G.vexlist[head->headvex].data << " ";
head = head->hlink;
}
cout << endl;
}
cout << endl;
}
int main() {
ALGraph G;
//输入样例:4 3 1 2 3 4 1 2 1 3 2 3
createGraph(G);
printGraph(G);
int selected;
while (true) {
cout << "输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出" << endl;
cin >> selected;
if (selected == 1) {
createArc(G);
} else if (selected == 2) {
deleteArc(G);
} else if (selected == 3) {
createVex(G);
} else if (selected == 4) {
deleteVex(G);
} else {
break;
}
printGraph(G);
}
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入顶点数量
4
请输入添加结点的值
0
添加结点成功
请输入添加结点的值
1
添加结点成功
请输入添加结点的值
2
添加结点成功
请输入添加结点的值
3
添加结点成功
请输入边的数量
7
输入边的起始点和终止点
0 1
0->1 创建成功
输入边的起始点和终止点
0 2
0->2 创建成功
输入边的起始点和终止点
2 0
2->0 创建成功
输入边的起始点和终止点
2 3
2->3 创建成功
输入边的起始点和终止点
3 0
3->0 创建成功
输入边的起始点和终止点
3 1
3->1 创建成功
输入边的起始点和终止点
3 2
3->2 创建成功
初始化十字链表成功
0 起始的边有: 0->2 0->1
0 结束的边有: 3->0 2->0
1 起始的边有:
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 3->2 0->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
1 2
1->2 创建成功
0 起始的边有: 0->2 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2 0->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
2
输入边的起始点和终止点
0 2
0->2 删除成功
0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
3
请输入添加结点的值
4
添加结点成功
0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
4 起始的边有:
4 结束的边有:
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
1 4
1->4 创建成功
0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->4 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
4 起始的边有:
4 结束的边有: 1->4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
输入边的起始点和终止点
4 3
4->3 创建成功
0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->4 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 4->3 2->3
4 起始的边有: 4->3
4 结束的边有: 1->4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
4
请输入删除的顶点
4
结点已删除
0 起始的边有: 0->1
0 结束的边有: 3->0 2->0
1 起始的边有: 1->2
1 结束的边有: 3->1 0->1
2 起始的边有: 2->3 2->0
2 结束的边有: 1->2 3->2
3 起始的边有: 3->2 3->1 3->0
3 结束的边有: 2->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
q
Process finished with exit code 0
2.4、邻接多重表
邻接多重表特点:
虽然邻接表已经能很好的表示无向图了,但是如果需要删除一条边<i, j>,则需要去 i,j 中分别删除相邻的结点
邻接多重表,每条边有个边结构体,删除时只需要删除一个边即可,但是要解除这个边的所有关系
邻接多重表中,边与边之间的联系相对密切,很容易找到与某个结点相关的边
邻接多重表结构:
顶点表结点:
mark:哨兵,用来标记当前边是否被访问过。
ivex:当前边相关联的一个结点。
ilink:指向上一条存在 ivex 结点的边。
jvex:当前边相关联的另一个结点。
jlink:指向上一条存在 jvex 结点的边。
info:表示顶点的值
在本篇博客中,做了ivex < jvex 的处理,
不做处理也可以实现,删除边时,相对于本篇博客的代码可能要做一些逻辑修改
邻接多重表例图:
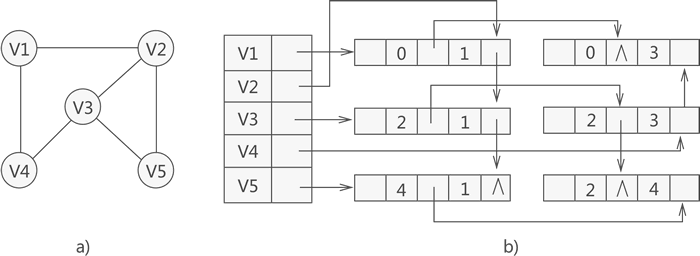
以 <2, 3> 这条边为例子:
可以通过 <2, 1> 这条边的 ilink 找到 <2, 3>
V4 (下标为3) 头结点的第一条相关边为 <2, 3>
可以通过 <2, 3> 这条边的 ilink 找到 <2, 4>
可以通过 <2, 3> 这条边的 jlink 找到 <0, 3>
边与边之间的联系相对密切,很容易找到与某个结点相关的边
邻接多重表示例代码
代码:
#include "iostream"
#define MAXSize 100
using namespace std;
typedef struct ArcNode { //边结构体:
bool visited; //记录此边是否被访问
int ivex, jvex; //记录此边的两个结点 i j(这里存放的是两个结点的下标)
// (笔者边结点保证了,下标小的为i,下标大的为j,如果不做处理,后面删除边也要修改逻辑)
struct ArcNode *ilink, *jlink; //ilink指向上一条和当前边 ivex 相同的边(上一条边的ivex 或者 jvex 和当前边的ivex相等)
// ,jlink也是指向上一条和 jvex 相关的边
int info; //用来记录这条边的权重
} ArcNode;
typedef struct VexNode { //结点结构体: 结点的值,firstedge指向与结点相关的第一条边
int data;
ArcNode *firstedge;
} VexNode;
typedef struct { //图结构体:结点的数组(表头为结点,结点后面跟指针),vexnum 结点的数量,arcnum 边结点的数量
VexNode adjmulist[MAXSize];
int vexnum, arcnum;
} AMLGraph;
//找到顶点在表头结点的下标
int getGraphIndex(AMLGraph G, int targetnode) { //通过结点的值,找到在图中表头结点的下标(如果不存在,返回-1)
for (int i = 0; i < G.vexnum; i++) {
if (G.adjmulist[i].data == targetnode) {
return i;
}
}
return -1;
}
//创建边
bool createArc(AMLGraph &G) {
int vex1, vex2, index1, index2;
cout << "请输入新建边的两个结点" << endl;
cin >> vex1 >> vex2;
index1 = getGraphIndex(G, vex1); //找到两个结点在结点数组中的下标
index2 = getGraphIndex(G, vex2);
ArcNode *newedge = new ArcNode; //构建一个新边
ArcNode *oldfirstegde; //!!!
if (index1 > index2) { //保证index1 <= index2 这么做是为了里面边的 i j 相对有序(如果不保证有序,但是后面删除边的逻辑要记得修改)
index1 ^= index2;
index2 ^= index1;
index1 ^= index2;
}
newedge->ivex = index1; //新边为i j 之间的边,边的两个结点要赋值i j
newedge->jvex = index2;
//把新边连接到下标index1 和 index2 两个头结点的第一条边
//相当于链表插入,头插法
oldfirstegde = G.adjmulist[index1].firstedge; //找到当前index1下标的结点的第一条边
G.adjmulist[index1].firstedge = newedge; //把新边绑定到index1的第一条边
newedge->ilink = oldfirstegde; //新边的ivex 和index1相等的,把老边绑定到新边的ilink
//与上面类似,是插入到index2头结点的第一条边
oldfirstegde = G.adjmulist[index2].firstedge;
G.adjmulist[index2].firstedge = newedge;
newedge->jlink = oldfirstegde;
G.arcnum++;
return true;
}
//通过下标找到边,在表头结点target相关的边 中 解除这条边的关系 //(target是index1 或者index2的其中一个)
bool deleteArc(AMLGraph &G, int index1, int index2, int target) { //找到一条下标index1 和 index2相关的边,删除下标 target 中此边的关系
ArcNode *curArc = G.adjmulist[target].firstedge; //找到target下标结点的第一条边
ArcNode *preArc; //记录当前边的上一条边,如果cur是要删除的边,直接pre下一条的关系连接到cur下一条的关系
int count = 0;
while (curArc) { //此边不为空,一直循环
count++; //每次循环一条边,count+1,,记录目标边是第几条
if (curArc->ivex == index1 && curArc->jvex == index2) { //如果找到此边,退出循环
break;
}
preArc = curArc; //当前边给pre,cur继续去找下一条边
//这里通过ivex 或者 jvex 找到下一条有关系的点
//如果 ivex 是 index1 或者 index2 ,就找ivex相关的下一条边,指向->ilink
if (curArc->ivex == index1 || curArc->ivex == index2) { //如果ivex结点为index1或者index2其中的一个
curArc = curArc->ilink;
//其他情况下就是 jvex 是 index1 或者 index2,就找jlink
} else {
curArc = curArc->jlink;
}
}
if (count == 0 || !curArc) { //如果没有循环,或者cur指向空结点了,说明没有此边
// cout << "当前边不存在" << endl;
return false;
} else if (count == 1) { //如果只循环了一次,说明是表头结点的第一条相关的边
if (curArc->ivex == target) { //如果是 ivex 结点与target相关 就把当前边的 ilink 赋值给表头结点的第一条边
G.adjmulist[target].firstedge = curArc->ilink;
} else { //否则就是 jvex 结点与target相关,把当前边的jlink给表头结点的第一条边
G.adjmulist[target].firstedge = curArc->jlink;
}
} else {
//如果pre的ivex 和 cur的ivex 相等,说明两个边都是通过 ilink 连接的,cur->ilink和pre->ilink是同一个ivex相关联的点
// 删除当前边的关系,把cur->ilink 赋值给pre->ilink
//这里举个例子:头结点下标为 0 的边 <0,1>,<0,2>,<0,3> cur指向<0,2> pre指向<0,1>
//两个边是通过 ivex 相连的,直接把pre->ilink 指向 cur->ilink (下面的大家可以自己举个例子理解理解)
if (preArc->ivex == curArc->ivex) {
preArc->ilink = curArc->ilink;
//pre->ivex和cur->jvex相关联 例子:头结点下标为 5 的边 <5,6>,<3,5>,<5,7>
} else if (preArc->ivex == curArc->jvex) {
preArc->ilink = curArc->jlink;
//例子:头结点下标为 5 的边 <0,5>,<5,7>,<3,5>
} else if (preArc->jvex == curArc->ivex) {
preArc->jlink = curArc->ilink;
//例子:头结点下标为 5 的边 <0,5>,<3,5>,<5,7>
} else if (preArc->jvex == curArc->jvex) {
preArc->jlink = curArc->jlink;
}
//一共就是这四种关系,大家可以多对应图,理解理解
}
return true;
}
//删除边
bool deleteArc(AMLGraph &G) {
int vex1, vex2, index1, index2;
cout << "请输入删除边的两个结点" << endl;
cin >> vex1 >> vex2;
index1 = getGraphIndex(G, vex1);
index2 = getGraphIndex(G, vex2);
if (index1 > index2) { //保证index1 <= index2 这么做是为了里面边的 i j 相对有序(如果没有这一步后面可能删除边会相对麻烦一些)
index1 ^= index2;
index2 ^= index1;
index1 ^= index2;
}
//删除index1 和 index2 相对于 index1 和 index2 头结点的关系
if (deleteArc(G, index1, index2, index1) && deleteArc(G, index1, index2, index2)) {
cout << vex1 << "->" << vex2 << "边删除成功" << endl;
return true;
} else {
cout << vex1 << "->" << vex2 << "边删除失败" << endl;
return false;
}
}
//创建结点
bool createVex(AMLGraph &G) {
cout << "请输入要创建的结点的值" << endl;
int data;
cin >> data;
G.adjmulist[G.vexnum].data = data; //给结点赋值,结点的第一条有关的边设为空,图中结点数量+1
G.adjmulist[G.vexnum].firstedge = NULL;
G.vexnum++;
return true;
}
//删除结点
bool deleteVex(AMLGraph &G) {
cout << "请输入要删除的结点" << endl;
int vex;
cin >> vex;
int index = getGraphIndex(G, vex); //找到要删除结点的下标
for (int i = 0; i < G.vexnum; i++) { //循环每个结点,删除所有结点与目标结点的关系
while (deleteArc(G, i, index, i)); //这里用while,是防止存在多条边的情况(当要删除的边不存在的时候会返回false)
while (deleteArc(G, i, index, index)); // 解除表头结点 i 中这条边的关系
}
G.adjmulist[index].data = -1; //结点删除后,把当前结点的值标记为 -1 ,表明该点已被删除
return true;
}
//初始化创建图
bool createAMLGraph(AMLGraph &G) {
cout << "请输入结点数" << endl;
int vexCount;
cin >> vexCount;
G.vexnum = 0; //初始化时,G的顶点数量为0
for (int i = 0; i < vexCount; ++i) {
createVex(G);
}
cout << "请输入边数" << endl;
int arcCount;
cin >> arcCount;
for (int i = 0; i < arcCount; ++i) {
createArc(G);
}
cout << "邻接多重表初始化完成" << endl;
return true;
}
//输出邻接多重表
bool printAMLGraph(AMLGraph G) {
for (int i = 0; i < G.vexnum; i++) { //循环图中的每一个点
if (G.adjmulist[i].data == -1) { //如果当前点的值为 -1 ,说明当前点已被删除
continue;
}
cout << G.adjmulist[i].data;
ArcNode *demo = G.adjmulist[i].firstedge;
while (demo) { //找到当前表头结点的第一个边,
cout << " " << demo->ivex << "<->" << demo->jvex; //输出当前边的两个结点
demo = demo->ivex == i ? demo->ilink : demo->jlink; //如果当前点的ivex与表头结点相关,就指向ilink,否则就是jvex与表头结点相关
}
cout << endl;
}
return true;
}
int main() {
AMLGraph G;
createAMLGraph(G); //初始化图
printAMLGraph(G);
int selected;
while (true) {
cout << "输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出" << endl;
cin >> selected;
if (selected == 1) {
createArc(G); //创建边
} else if (selected == 2) {
deleteArc(G); //删除边
} else if (selected == 3) {
createVex(G); //创建结点
} else if (selected == 4) {
deleteVex(G); //删除结点
} else {
break;
}
printAMLGraph(G); //每次都输出图
}
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
请输入结点数
4
请输入要创建的结点的值
0
请输入要创建的结点的值
1
请输入要创建的结点的值
2
请输入要创建的结点的值
3
请输入边数
5
请输入新建边的两个结点
0 1
请输入新建边的两个结点
0 2
请输入新建边的两个结点
0 3
请输入新建边的两个结点
1 3
请输入新建边的两个结点
2 3
邻接多重表初始化完成
0 0<->3 0<->2 0<->1
1 1<->3 0<->1
2 2<->3 0<->2
3 2<->3 1<->3 0<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
请输入新建边的两个结点
1 2
0 0<->3 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3 0<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
2
请输入删除边的两个结点
0 3
0->3边删除成功
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
3
请输入要创建的结点的值
4
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
1
请输入新建边的两个结点
1 4
0 0<->2 0<->1
1 1<->4 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
4 1<->4
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
4
请输入要删除的结点
4
0 0<->2 0<->1
1 1<->2 1<->3 0<->1
2 1<->2 2<->3 0<->2
3 2<->3 1<->3
输入 1 添加边, 输入 2 删除边, 输入 3 添加结点, 输入 4 删除结点, 输入其他退出
q
Process finished with exit code 0
三、图的遍历
3.1、深度优先搜索
深度优先搜索概念:
深度优先搜索: 是沿着一个方向访问到底,访问过的点,进行标记,然后在从底换一个方向继续访问,访问下一个点的时候,如果被 标记过就不在访问。直到所有的点都被标记了,说明每个点都被访问了。
其实有点类似树的递归遍历(先,中,后序遍历),先向左下方向找到底,然后在返回上一个结点的右子树接着找, 找完继续返回上个结点,换个方向继续找,不断这么重复递归,即可完成所有结点的遍历
总之,记住一句话,深度优先查找就是先尽可能达到当前遍历路径能够达到最长的路径,一旦达到该路径终点,再回 溯,从原来已遍历过顶点(PS:该顶点包含多个分支路径)处开始新的分支路径遍历。
深度优先搜索例图:

深度优先搜索的方向顺序,起点可以自己选择
这里我们先从左下方向搜,然后再向右下方向走,然后右上,左上
例如:从 V1 开始 访问 V1,V1 标记已访问
V1 -> V2 V2 标记已访问,继续向这个方向搜索下一个
V2 -> V4 V4 标记已访问,继续向这个方向搜索
V4 -> V8 V4 左下方向已经没有结点了,找右下方向 V8 ,V8标记访问
V8 -> V5 V8 下方没有结点了,找左上 V5 ,V5标记访问
V1 -> V3 V5相连的没有未访问的结点了,只能返回V5->V8->V4->V2->V1 ,V1 以前的结点都被访问了,访问V3,标记V3已访问
V3 -> V6 V6 标记已访问,继续向这个方向搜索
V6 -> V7 V6 左下方向已经没有结点了,找右下方向 V7 ,V7标记访问
V7 没有未访问结点了,返回 V7->V6->V3->V1 全部访问了,图遍历完成
V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7
深度优先搜索示例代码(邻接矩阵存储图):
此处借用算法设计与分析基础(第三版)上一段概念介绍,及说明图形介绍其具体遍历过程,下面的具体代码使用数据就是下图中相关数据。

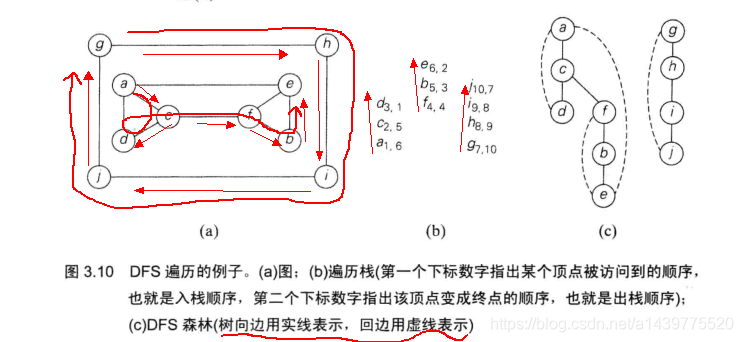
代码:
#include "iostream"
using namespace std;
int count = 0; //用于计算遍历总次数
int value[10]; //初始化后,各元素均为0
char result[10];
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历
* result用于存放深度优先遍历的顶点顺序
* number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
*/
void dfsVisit(int adjMatrix[10][10], int number) {
value[number] = ++count; //把++count赋值给当前正在遍历顶点判断值数组元素,变为非0,代表已被遍历
cout << "当前已行走顶点value[" << number << "] = " << value[number] << " ";
for (int i = 0; i < 10; i++) {
if (adjMatrix[number][i] == 1 && value[i] == 0) { //当当前顶点的相邻有相邻顶点可行走且其为被遍历
char temp = (char) ('a' + i);
result[count] = temp; //存放即将行走的顶点下标字母
cout << " 当前i值:" << i << " 到达" << temp << "地" << endl;
dfsVisit(adjMatrix, i); //执行递归,行走第i个顶点
}
}
}
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历
* result用于存放深度优先遍历的顶点顺序
*/
void dfs(int adjMatrix[10][10] ) {
for (int i = 0; i < 10; i++) {
if (value[i] == 0) {
char temp = (char) ('a' + i);
cout << "深度为:" << i << ",当前出发点:" << temp << endl;
result[i] = temp; //存放当前正在遍历顶点下标字母
dfsVisit(adjMatrix, i);
}
}
}
int main() {
int adjMatrix[10][10] = {{0, 0, 1, 1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 1, 0, 0, 0, 0},
{1, 0, 0, 1, 0, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 1, 1, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0}};
dfs(adjMatrix);
cout << endl << "深度优先查找遍历顺序如下:" << endl;
for (int i = 0; i < 10; i++)
cout << " " << result[i];
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
深度为:0,当前出发点:a
当前已行走顶点value[0] = 1 当前i值:2 到达c地
当前已行走顶点value[2] = 2 当前i值:3 到达d地
当前已行走顶点value[3] = 3 当前i值:5 到达f地
当前已行走顶点value[5] = 4 当前i值:1 到达b地
当前已行走顶点value[1] = 5 当前i值:4 到达e地
当前已行走顶点value[4] = 6 深度为:6,当前出发点:g
当前已行走顶点value[6] = 7 当前i值:7 到达h地
当前已行走顶点value[7] = 8 当前i值:8 到达i地
当前已行走顶点value[8] = 9 当前i值:9 到达j地
当前已行走顶点value[9] = 10
深度优先查找遍历顺序如下:
a c d f b e g h i j
Process finished with exit code 0
3.2、广度优先搜索
广度优先搜索概念:
广度优先查找(Breadth-first Search,BFS)按照一种同心圆的方式,首先访问所有和初始顶点邻接的顶点,然后是离它两条边的所有未访问顶点,以此类推,直到所有与初始顶点同在一个连通分量中的顶点都被访问过了为止。如果仍然存在未被访问的顶点,该算法必须从图的其他连接分量中的任意顶点重新开始。
广度优先搜索例图:
百度百科:
1代表第一步要走的点,2代表第二步要走的点……
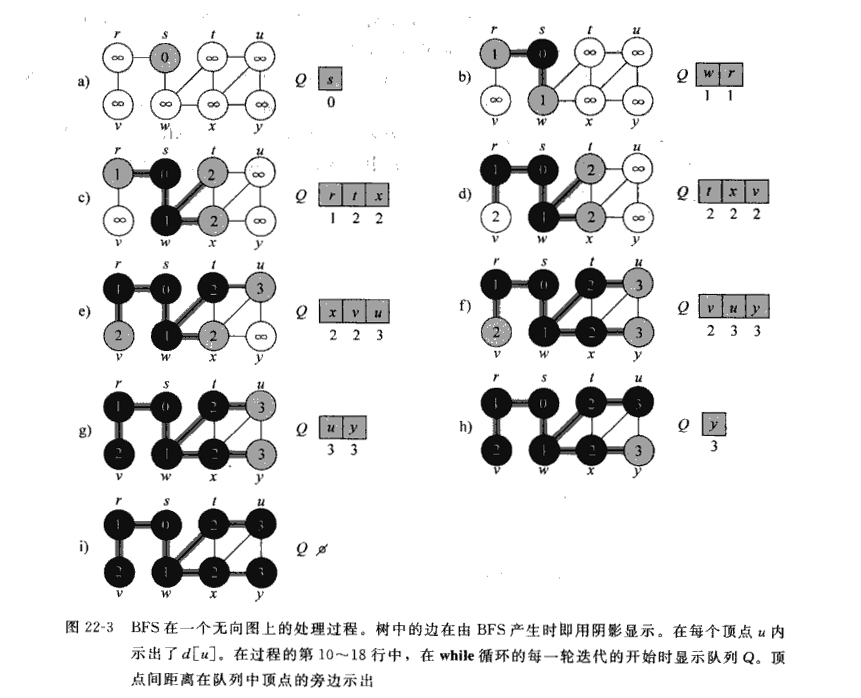
广度优先搜索示例代码(邻接矩阵存储图):
此处借用《算法设计与分析基础》(第3版)上一段文字介绍及其配图来讲解,下面程序中使用的图就是配图中所给的数据,在程序中,使用邻接矩阵来表示配图中图。

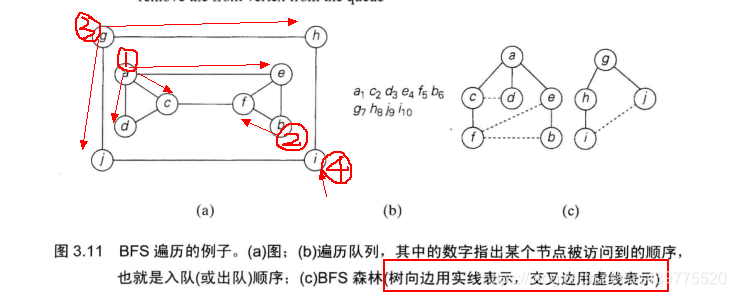
PS:下面所给程序的运行结果和配图中图(b)顺序在fb那两个位置不一致,下面程序运行结果顺序是a c d e b f g h j i,原因是在遍历的过程中,我所写代码是按照字母顺序来进行遍历的,书上所讲可能是使用链表来存储顶点,具体怎么实现本人也未去仔细探讨…
代码:
#include "iostream"
using namespace std;
int count = 0; //用于计算遍历总次数
int value[10]; //初始化后,各元素均为0
char result[10];
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历,其最终具体结果代表该顶点在最终遍历顺序中的位置
* result用于存放广度优先遍历的顶点顺序
* number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
*/
void bfsVisit(int adjMatrix[10][10] ,int number){
value[number] = ++count; //出发顶点已被遍历,其在遍历结果中最终位置为++count
for(int i = 0;i < 10;i++){
if(adjMatrix[number][i] == 1 && value[i] == 0){ //当改顶点与出发顶点相邻且未被遍历时
char temp = (char) ('a' + i);
result[count] = temp;
cout << endl;
cout << "到达" << temp << "地" << "\t";
value[i] = ++count; //当前被遍历顶点,其在遍历结果中最终位置为++count
}
}
}
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历,其最终具体结果代表该顶点在最终遍历顺序中的位置
* result用于存放广度优先遍历的顶点顺序
*/
void bfs(int adjMatrix[10][10]){
for(int i = 0;i < 10;i++){
if(value[i] == 0){ //当该顶点未被遍历时
char temp = (char) ('a' + i);
result[count] = temp;
cout << endl << "出发点:" << temp << "地";
bfsVisit(adjMatrix,i); //使用迭代遍历该顶点周边所有邻接顶点
}
}
}
int main() {
int adjMatrix[10][10] = {{0, 0, 1, 1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 1, 0, 0, 0, 0},
{1, 0, 0, 1, 0, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 1, 1, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0}};
bfs(adjMatrix);
cout << endl << "广度优先查找遍历顺序如下:" << endl;
for (int i = 0; i < 10; i++)
cout << " " << result[i];
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
出发点:a地
到达c地
到达d地
到达e地
出发点:b地
到达f地
出发点:g地
到达h地
到达j地
出发点:i地
广度优先查找遍历顺序如下:
a c d e b f g h j i
Process finished with exit code 0
3.3、Dijkstra最短路径
Dijkstra概念:
Dijkstra算法功能:给出加权连通图中一个顶点,称之为起点,找出起点到其它所有顶点之间的最短距离。
Dijkstra算法思想:采用贪心法思想,进行n-1次查找(PS:n为加权连通图的顶点总个数,除去起点,则剩下n-1个顶点),第一次进行查找,找出距离起点最近的一个顶点,标记为已遍历;下一次进行查找时,从未被遍历中的顶点寻找距离起点最近的一个顶点, 标记为已遍历;直到n-1次查找完毕,结束查找,返回最终结果。
Dijkstra例图:
使用Dijkstra算法得到最短距离示例
此处借用文末参考资料1博客中一个插图(PS:个人感觉此图描述简单易懂):
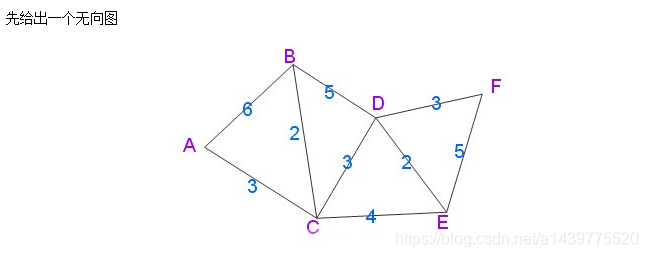

Dijkstra示例代码(邻接矩阵存储图):
Dijkstra复杂度是O(N^2),如果用binary heap优化可以达到O((E+N)logN),用fibonacci heap可以优化到O(NlogN+E) 。
注意,Dijkstra算法只能应用于不含负权值的图。因为在大多数应用中这个条件都满足,所以这种局限性并没有影响Dijkstra算法的广泛应用。
其次,大家要注意把Dijkstra算法与寻找最小生成树的Prim算法区分开来。两者都是运行贪心法思想,但是Dijkstra算法是比较路径的长度,所以必须把起点到相应顶点之间的边的权重相加,而Prim算法则是直接比较相应边给定的权重。
下面的代码时间复杂度为O(N^2),代码中所用图为2.1使用Dijkstra算法得到最短距离示例中所给的图。
代码:
#include "iostream"
using namespace std;
/*
* 参数adjMatrix:为图的权重矩阵,权值为-1的两个顶点表示不能直接相连
* 函数功能:返回顶点0到其它所有顶点的最短距离,其中顶点0到顶点0的最短距离为0
*/
int result[6]; //用于存放顶点0到其它顶点的最短距离
void getShortestPaths(int adjMatrix[6][6]) {
bool used [6] ; //用于判断顶点是否被遍历
used[0] = true; //表示顶点0已被遍历
for(int i = 1;i < 6;i++) {
result[i] = adjMatrix[0][i];
used[i] = false;
}
for(int i = 1;i < 6;i++) {
int min = 0xffff; //用于暂时存放顶点0到i的最短距离,初始化为Integer型最大值
int k = 0;
for(int j = 1;j < 6;j++) { //找到顶点0到其它顶点中距离最小的一个顶点
if(!used[j] && result[j] != -1 && min > result[j]) {
min = result[j];
k = j;
}
}
used[k] = true; //将距离最小的顶点,记为已遍历
for(int j = 1;j < 6;j++) { //然后,将顶点0到其它顶点的距离与加入中间顶点k之后的距离进行比较,更新最短距离
if(!used[j]) { //当顶点j未被遍历时
//首先,顶点k到顶点j要能通行;这时,当顶点0到顶点j的距离大于顶点0到k再到j的距离或者顶点0无法直接到达顶点j时,更新顶点0到顶点j的最短距离
if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))
result[j] = min + adjMatrix[k][j];
}
}
}
}
int main() {
int adjMatrix[6][6] = {{0,6,3,-1,-1,-1},
{6,0,2,5,-1,-1},
{3,2,0,3,4,-1},
{-1,5,3,0,2,3},
{-1,-1,4,2,0,5},
{-1,-1,-1,3,5,0}};
getShortestPaths(adjMatrix);
cout << "顶点0到图中所有顶点之间的最短距离为:" << endl;
for(int i = 0;i < 6;i++)
cout << result[i] << " ";
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
顶点0到图中所有顶点之间的最短距离为:
0 5 3 6 7 9
Process finished with exit code 0
3.4、Floyd最短路径
Floyd概念:
Floyd算法功能:给定一个加权连通图,求取从每一个顶点到其它所有顶点之间的最短距离。(PS:其实现功能也称完全最短路径问题)
Floyd算法思想:将顶点i到j的直接距离依次与顶点i到顶点j之间加入k个中间节点之后的距离进行比较,从中选出最短的一组距离,即为顶点i到顶点j的最短距离,然后重复上述步骤求取其它顶点之间的最短距离。
Floyd例图:
使用Floyd算法得到最短距离示例**
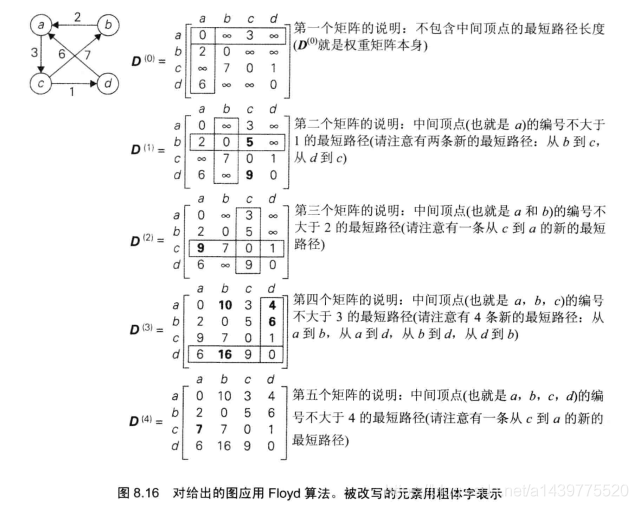
此处借用《算法设计与分析基础》第3版上一个插图:
其中,
D(0)表示不包含中间节点,即给定图的原始权重矩阵;
D(1)表示加入一个中间节点a;
D(2)表示在D(1)的基础上再加入一个中间节点b;
D(3)表示在D(2)的基础上再加入一个中间节点c;
D(4)表示在D(3)的基础上再加入一个中间节点d,这时就可得到最终结果。
每次加入一个中间节点后,都要更新所有顶点之间的最短距离,直到所有顶点均可以作为中间顶点之后,才算更新完毕,即可得到最终结果。
Floyd示例代码(邻接矩阵存储图):
Floyd是计算每对顶点间最短路径的经典算法,其采用的思想是动态规划法。
时间复杂度是雷打不动的O(n^3)。
注意,Floyd算法计算最短距离可以有负权值的边,但不能有权值和为负数的回路。
下面代码中所用图的数据便是2.1中示例图的数据。
代码:
#include "iostream"
using namespace std;
/*
* 参数adjMatrix:给定连通图的权重矩阵,其中权重为-1表示两个顶点不能直接相连
* 函数功能:返回所有顶点之间的最短距离权重矩阵
*/
void getShortestPaths(int adjMatrix[4][4]) {
for (int k = 0; k < 4; k++) {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (adjMatrix[i][k] != -1 && adjMatrix[k][j] != -1) {
int temp = adjMatrix[i][k] + adjMatrix[k][j]; //含有中间节点k的顶点i到顶点j的距离
if (adjMatrix[i][j] == -1 || adjMatrix[i][j] > temp)
adjMatrix[i][j] = temp;
}
}
}
}
}
int main() {
int adjMatrix[4][4] = {{0, -1, 3, -1},
{2, 0, -1, -1},
{-1, 7, 0, 1},
{6, -1, -1, 0}};
getShortestPaths(adjMatrix);
cout << "使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:" << endl;
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
cout << adjMatrix[i][j] << " ";
}
cout << endl;
}
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:
0 10 3 4
2 0 5 6
7 7 0 1
6 16 9 0
Process finished with exit code 0
3.5、Prim最短路径
Prim概念:
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
原理简单介绍:
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
Prim例图:
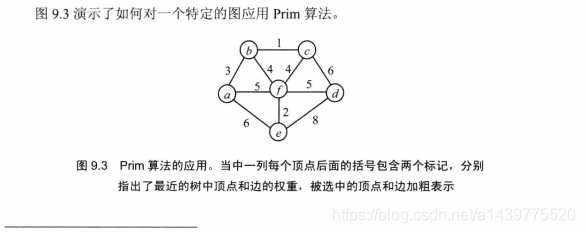
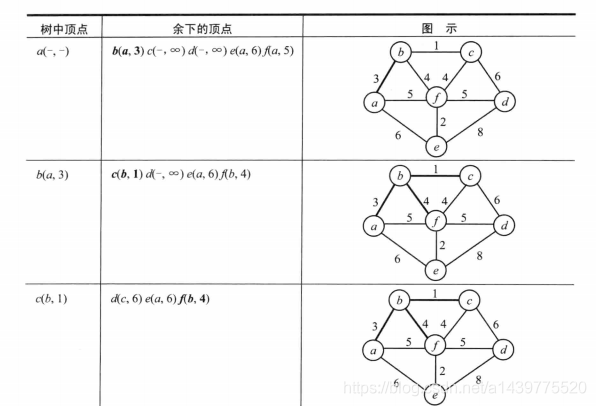
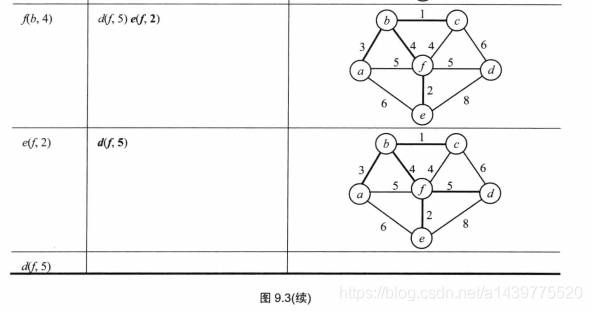
本文具体编码使用数据参考自《算法设计与分析基础》第三版,下面是其具体图示:
Prim示例代码(邻接矩阵存储图):
代码:
#include "iostream"
#include "vector"
using namespace std;
/*
* 参数G:给定的图,其顶点分别为0~G.length-1,相应权值为具体元素的值
* 函数功能:返回构造生成的最小生成树,以二维数组形式表示,其中元素为0表示最小生成树的边
*/
void getMinTree(int G[6][6]) {
int result[6][6] = {{-1, 3, -1, -1, 6, 5},
{3, -1, 1, -1, -1, 4},
{-1, 1, -1, 6, -1, 4},
{-1, -1, 6, -1, 8, 5},
{6, -1, -1, 8, -1, 2},
{5, 4, 4, 5, 2, -1}};
int vertix[6]; //记录顶点是否被访问,如果已被访问,则置相应顶点的元素值为-2
for (int i = 0; i < 6; i++)
vertix[i] = i;
vector<int> listV; //保存已经遍历过的顶点
listV.push_back(0); //初始随意选择一个顶点作为起始点,此处选择顶点0
vertix[0] = -2; //表示顶点0被访问
while (listV.size() < 6) { //当已被遍历的顶点数等于给定顶点数时,退出循环
int minDistance = 0xffff; //用于寻找最小权值,初始化为int最大值,相当于无穷大的意思
int minV = -1; //用于存放未被遍历的顶点中与已被遍历顶点有最小权值的顶点
int minI = -1; //用于存放已被遍历的顶点与未被遍历顶点有最小权值的顶点 ;即G[minI][minV]在剩余的权值中最小
for (int i = 0; i < listV.size(); i++) { //i 表示已被访问的顶点
int v1 = listV[i];
for (int j = 0; j < 6; j++) {
if (vertix[j] != -2) { //满足此条件的表示,顶点j未被访问
if (G[v1][j] != -1 && G[v1][j] < minDistance) {//G[v1][j]值为-1表示v1和j是非相邻顶点
minDistance = G[v1][j];
minV = j;
minI = v1;
}
}
}
}
vertix[minV] = -2;
listV.push_back(minV);
result[minI][minV] = 0;
result[minV][minI] = 0;
}
cout << "使用Prim算法,对于给定图中的顶点访问顺序为:" << endl;
for (int i = 0; i < listV.size(); i++) {
cout << listV[i] << " ";
}
cout << endl;
cout << "使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边):" << endl;
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++)
cout << result[i][j] << "\t";
cout << endl;
}
}
int main() {
int G[6][6] = {{-1, 3, -1, -1, 6, 5},
{3, -1, 1, -1, -1, 4},
{-1, 1, -1, 6, -1, 4},
{-1, -1, 6, -1, 8, 5},
{6, -1, -1, 8, -1, 2},
{5, 4, 4, 5, 2, -1}};
getMinTree(G);
return 0;
}
输入输出样例:
/home/a1439775520/CLionProjects/Graph/cmake-build-debug/Graph
使用Prim算法,对于给定图中的顶点访问顺序为:
0 1 2 5 4 3
使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边):
-1 0 -1 -1 6 5
0 -1 0 -1 -1 0
-1 0 -1 6 -1 4
-1 -1 6 -1 8 0
6 -1 -1 8 -1 0
5 0 4 0 0 -1
Process finished with exit code 0