《Two-Dimensional PCA: A New Approach to Appearance-Based Face Representation and Recognition》
本人机器学习的论文阅读部分学习了2D-PCA的原始文献《Two-Dimensional PCA: A New Approach to Appearance-Based Face Representation and Recognition》以下是自己通过阅读整理出的PCA和2D-PCA的相关知识,供参考嘻嘻~

一、PCA理解
-
PCA作用:降维
一般情况下,在机器学习中数据被表示为向量,如(a, b, c, d, e)T称为一条记录,当记录的维度成千上万时会带来大量的计算。实际发现记录中的每一列存在相关性,当删去时对结果的影响很小甚至几乎为0,因此可对数据进行降维,而降维意味着数据丢失,我们的目的是在降维的同时将信息的损失尽量降低。(引入投影概念,若将每条记录以坐标的形式投影到一条直线上,重合的数据即为丢失的信息) -
投影:*(a,b)=|a|*|b|cosθ
笛卡尔坐标系的坐标其实就是x坐标和y坐标在x轴正方向和y轴的正方向上的投影,这里默认x和y轴为单位向量,即当(a,b)=|a|*|b|*cosθ公式中当|a|为1,即是单位向量时,b在a上的投影就是b的坐标值如下图。这就将坐标转换成了投影,我们要获得不重合的坐标,就要保证投影的向量是尽量不相关的。
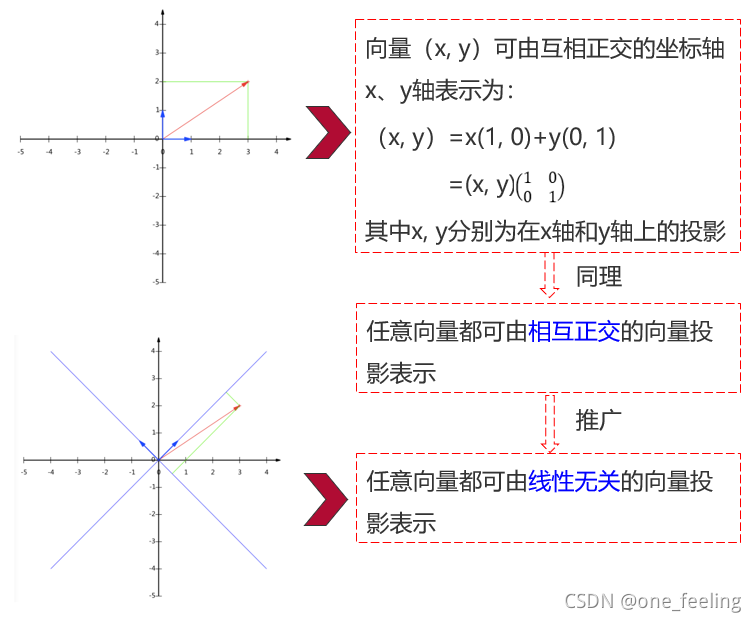
-
将二维推广到多维,我们降维的目标就变成了找n维向量在互相正交的向量下的投影坐标。由此目标转换为找到d个相互正交的向量,由此联想到矩阵的特征向量。
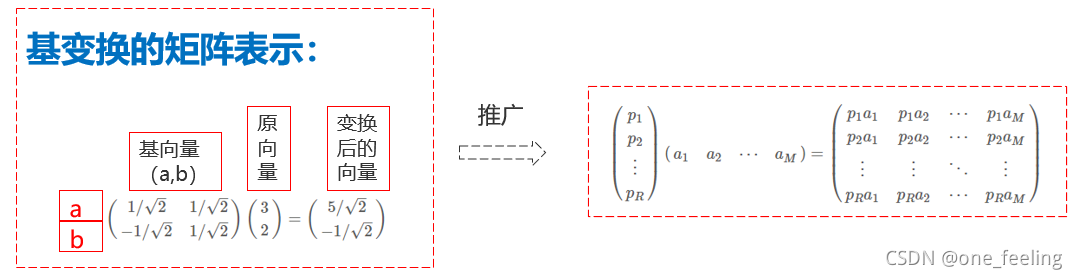
其中我们的输入是M个n维列向量,我们将输入由R个相互正交的向量表示,此时这R个向量是标准正交化后的单位向量,由上面我们推论过的若向量是单位化的,则做乘积后就是原向量在该单位向量上的坐标,所以我们做乘积,获得新的坐标。(RN)(NM)=(RM),原始矩阵大小为NM,获得的转换后的矩阵为RM,若R<N,则降维的目的实现。此时目标就是找到R个相互正交的标准化后的单位向量。 -
如何确定R个标准正交化的向量-SVD分解
首先引入方差、协方差的概念:
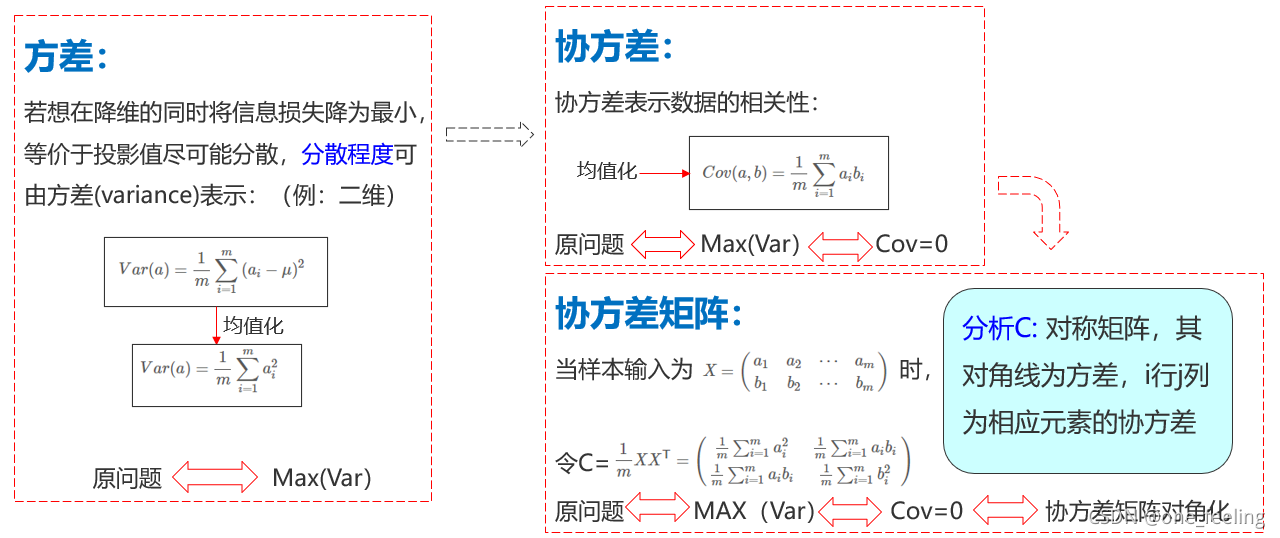
首先将原问题等价为求最大方差->协方差为0->协方差矩阵对角化,最后我们就要找到协方差矩阵的对角化形式。
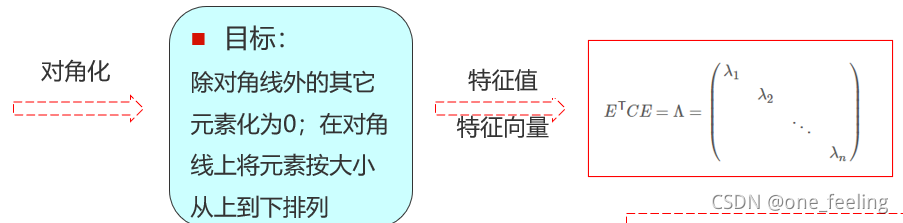
这里之所以将特征值按从大到小排列的原因是因为我们要使得方差(即对角线)最大,从另一个角度,我们要找到R个线性无关的特征向量,而矩阵的大部分特征基本上排列在前k大的特征向量中,在论文中也有验证,所以我们要将其按顺序排列。
接下来就要找矩阵的特征值和特征向量(类似于矩阵的SVD分解)。 -
至此PCA的相关原理就解释完毕,总结思路就是:
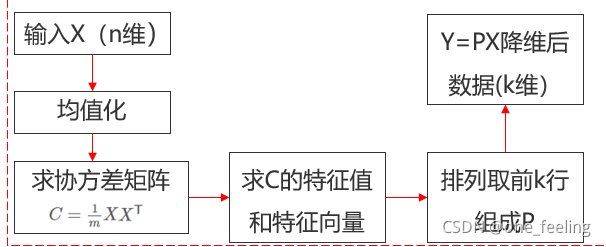
而2D-PCA与PCA的不同之处就是2D-PCA输入的是矩阵而不是一维向量,以人脸识别为例,2D-PCA输入的是图像,而PCA是将图像转变为一维向量之后再进行接下来的处理,当图片很大时,处理成本较高,所以就出现了2D-PCA。
二、2D-PCA
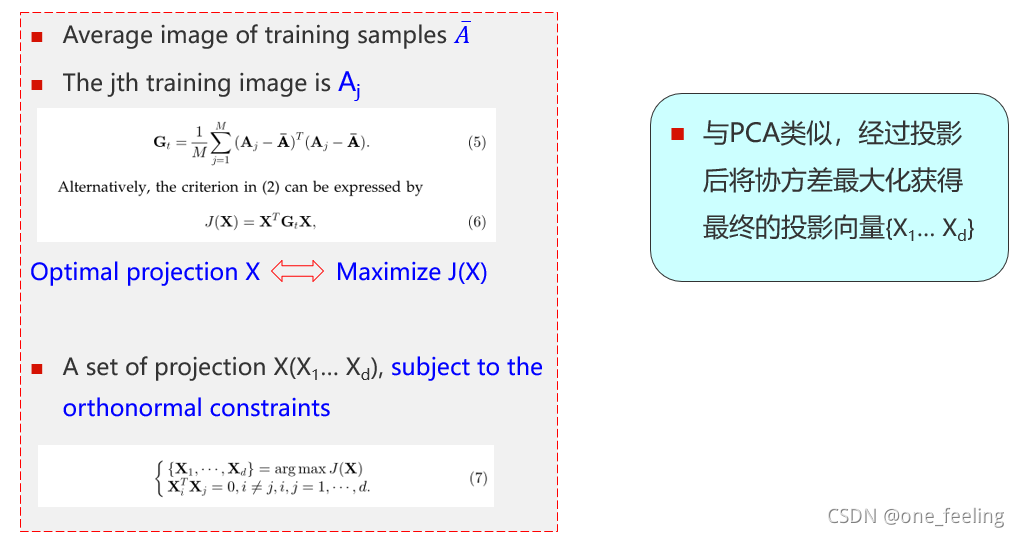
-解题思路是一样的,只不过在获得投影向量时使用矩阵而不是向量,在进行原图像在投影向量上的投影时输入的是图像矩阵而不是一维向量。在这篇论文中,他们的输入、协方差矩阵分别如下:

三、论文涉及的实验
-
实验内容:使用三个人脸数据库对人脸进行识别和重构
包括特征提取、人脸重构等
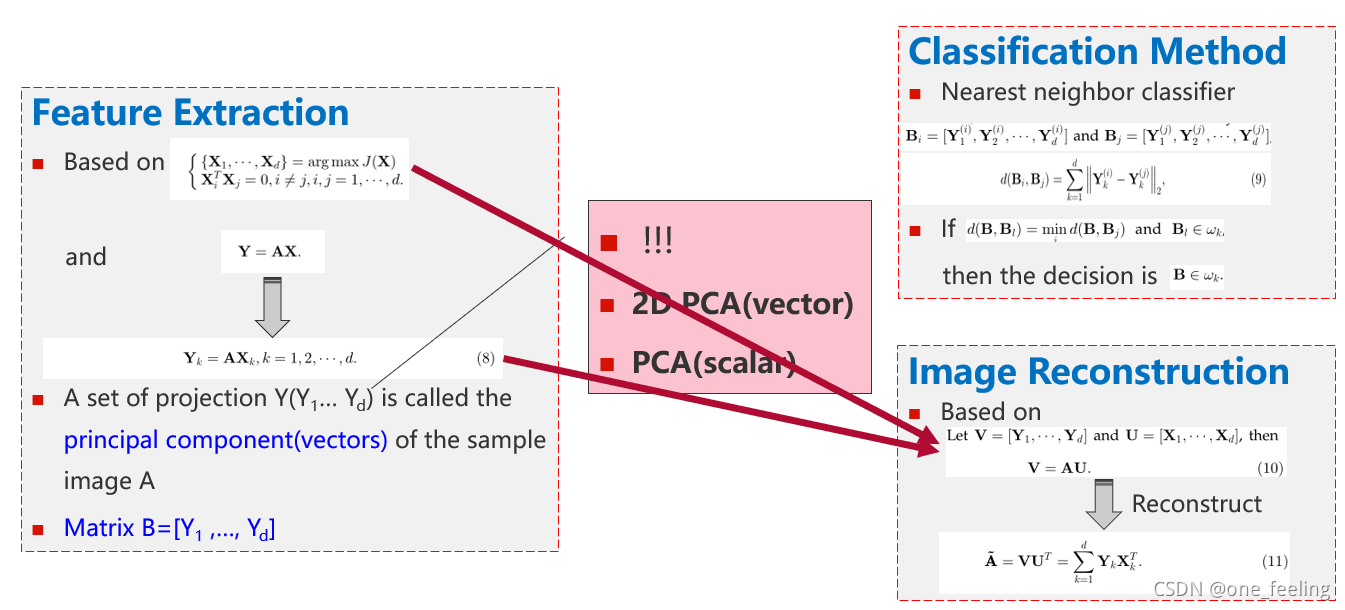
人脸重构就是通过提取出的人脸图像的特征向量,在此基础上重构回原始的人脸图像,即用局部还原总体。 -
实验一(ORL人脸数据库)

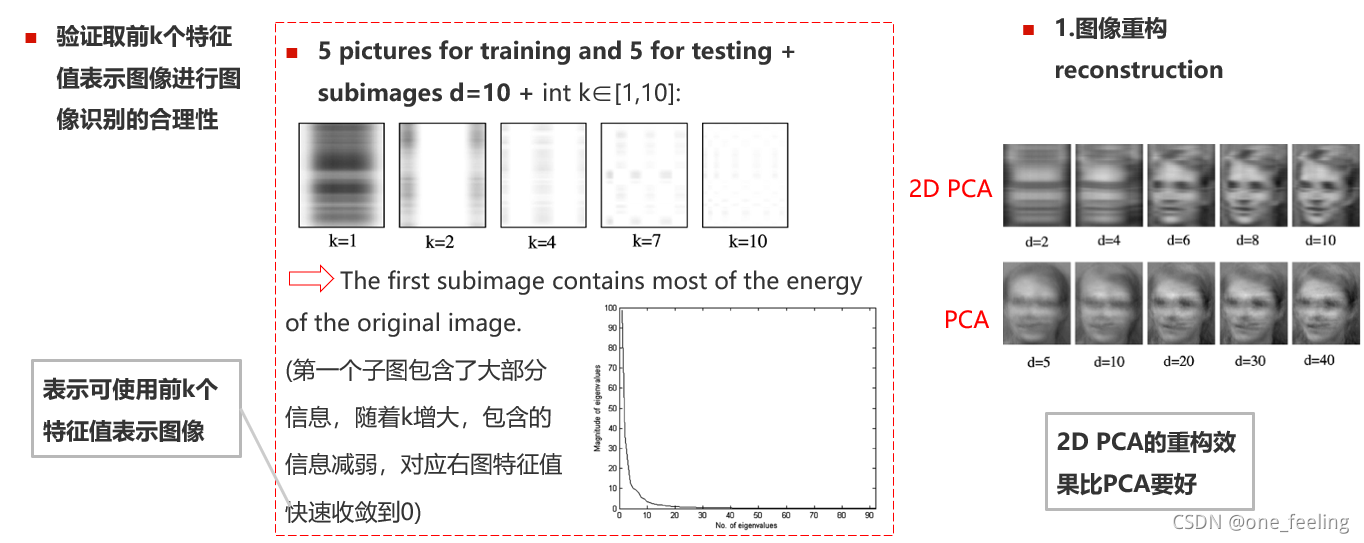
在这一部分作者验证了使用前k大个特征向量作为人脸识别和重构的合理性,从图中可以看到图像的大部分信息都集中在前几个大的特征值中。
作者还与其他实验进行了对比实验,结果2D-PCA基本上都比当时其他识别方法要好。 -
实验二(AR人脸数据库)

-
实验三(Yale人脸数据库)

写在最后
写给自己看~
(这篇博客主要从数学原理层面解释了PCA的原理,是本人的第一篇博客,希望以后可以养成写博客的好习惯,梳理思路的同时也可以为别人提供一丢丢帮助,开森。~ 写博客也是受到了男朋友的启发和鼓励,他是一个很有魅力很优秀的男生,我也要跟上他的脚步。虽是异地,会遇到很多问题,比如自己会想到无法参与彼此的生活呀,不能牵着彼此的手靠着彼此的肩膀呀,不能实际参与到Ta的点点滴滴的生活呀,这些有时会让人很失落,但是彼此在一起的回忆就显得更美好,更值得珍惜了呀嘻嘻,要开心快乐地过好自己的生活,我们都会陪着彼此哒。我坚信我们可以长长久久、一直一直牵手走下去的~)