本次实验的所有代码已上传个人github仓库：https://github.com/Scienthusiasts/Machine-Learning

Logistic 回归实现手势识别

其实好久以前博主本人就有构思实现一个有界面的完整的手势识别系统，即不仅可以实现手部姿态的检测，还能判断手部的姿势对应所要表达的信息。基于这个想法可以实现很多事情，比如说根据手势进行隔空绘图，操作游戏场景等等(可以和VR结合)，除此之外还可以控制鼠标，控制PPT翻页等。基于手势识别的应用前景可以说是非常广泛的(也可以拿来搞课设🐛🐛🐛)。

1. 想法构思

现有的网上开源的手势识别算法主要基于两种思路：

一是通过图像形态学处理，肤色检测，图像滤波等方法提取出手部轮廓或者手部边缘，再根据边缘信息提取出手部特征。在进行识别时将测试数据与建立的手部特征进行比对，这是基于传统数字图像处理的方法。

图像来源：基于OpenCV的手势识别完整项目（Python3.7）

另一个则是走深度学习的路线，通过深度网络提取出手部区域及关键点(本质也是一个回归+分类问题)，再进行常规操作(比如比较关键点之间的夹角判断姿态等)。或者直接基于目标检测算法、卷积神经网络训练大量的手势图片，这和经典的图像识别/目标检测类似。

基于OpenPose的手部关键点检测：

为了和当前博主正在学习的机器学习算法联系起来，在本篇博客中，我们暂不考虑如何实现手部关键点的回归问题，仅考虑分类问题。因此博主将会基于Mediapipe开源深度学习工具包里的手部姿态检测算法提取手部关键点。然后基于这些关键点进行手势的分类。

mediapipe手部关键点检测包含21个手部关键点：

Mediapipe API传送门:https://google.github.io/mediapipe/solutions/hands

一些细节

事实上，博主也曾想过直接通过录制大量的手势图像，然后直接将这些图像喂入算法进行训练。但这实际上有一些问题：我们知道，相较于直接使用关键点进行预测，图像实则包含了更多的细节特征，然而相应的这也会带来过多的噪声。对于logistic regression这样简单的线性二分类算法而言，可能难以训练出泛化性能较好的参数，因此，只选择手部关键点作为训练数据可能是一个上策。

但是，我们又该如何预处理这些关键点使其能够表达姿态信息呢？博主一开始的想法是使用关键点的坐标。然而坐标实际上是绝对的，如果手部出现在图像中的位置不同但手势完全相同，它们的坐标也是不同的，这就会给算法的训练增添而外的负担。一个想法是使用关键点之间的距离，即关键点两两之间的距离作为训练数据的维度(这样不仅能够保证姿态数据的平移不变性，同样也能够保证旋转不变性：在三维坐标下，不同角度的两个相同姿态的手势它们各自两两关键点之间的距离是相同的)

好，训练数据既然选定，那就说干就干，效果好不好再说。

2. 实现流程

2.1 数据采集与预处理

2.1.1基于mediapipe工具包的手部关键点提取

mediapipe网站已经为我们提供了完整的手部关键点检测的相关API以及Python 代码实现，我们要做的只是Ctrl C V，不过一些细节仍然要改下：

  ... ...  
    if results.multi_hand_landmarks:
        for hand_landmarks in results.multi_hand_landmarks:
  ... ...

在相关代码的这两行下就是提取的手部关键点，我们可以输出hand_landmarks这个变量一探究竟：

... ...
landmark {
  x: 0.9662408828735352
  y: 0.5577888488769531
  z: -0.23717156052589417
}
... ...

通过观察可以发现，hand_landmarks变量下包含了21个landmark属性，因此我们可以断定每一个landmark就对应一个手部关键点，其中每个landmark下又有x,y,z三个属性，很明显这便是每个关键点的空间坐标(mediapipe集成的算法可以通过单目相机预测出关键点相对于手掌关键点的深度)。不过它们都在(0,1)这个区间内，因此这些坐标应该是被归一化处理过的。

提取坐标的代码：

... ...
keypoint = []
for i in range(21):
	x = hand_landmarks.landmark[i].x
	y = hand_landmarks.landmark[i].y
	z = hand_landmarks.landmark[i].z
    keypoint.append([x,y,z])
keypoint = np.array(keypoint)
... ...

然后记住keypoint这个变量的shape:[21,3]

只提取一帧手势关键点用来训练算法显然是不够的，因此，对每个手势我们提取500帧关键点并整合为一个数据集，并保存在position变量中，最后转存为numpy二进制文件：

... ...
    if CNT<500:
        cv2.putText(image, str(CNT), (30,30), cv2.FONT_HERSHEY_SIMPLEX, .6, (0, 255, 0), 1)
        position.append(keypoint)
        CNT += 1
... ...
position = np.array(position)
print(position.shape)
np.save('./hand_frames.npy', position)
... ...

然后记住position这个变量的shape:[500,21,3]

手部关键点可视化

得到了手部500帧的关键点坐标，接下来就可以进行预处理转化为关键点两两之间的距离。不过在此之前，我觉得先可视化一下这500帧关键点应该也蛮有意思的哈哈🤣

手部关键点可视化：

# 绘制随时间变化下的手势数据集
def draw(X, ax, step):
    lines = []
    # 绘制点与点之间的连线
    lines.append(X[[0,1,2,3,4]])
    lines.append(X[[0,5,6,7,8]])
    lines.append(X[[0,17,18,19,20]])
    lines.append(X[[5,9,13,17]])
    lines.append(X[[9,10,11,12]])
    lines.append(X[[13,14,15,16]])
    for line in lines:
        ax.plot(line[:,0], line[:,1], line[:,2], linewidth=2)
        ax.set_xlim(0,1)
        ax.set_ylim(0,1)
        ax.set_zlim(-0.5,0.5)
    plt.pause(0.01)
    plt.cla()

# 三维手势数据集可视化
def show_frames(hand_frame):
    fig = plt.figure()
    # 3D绘图
    ax = fig.add_subplot(111, projection='3d')
    for step, hand in enumerate(hand_frame):
        draw(hand, ax, step)

if __name__ == "__main__":
    # 录制的手势数据集
    hand_frames = np.load('./hand_frame/hand_frame_one.npy')
    show_frames(hand_frames)

可视化效果(左图为五指张开的姿态，右图为紧握双拳的姿态)：

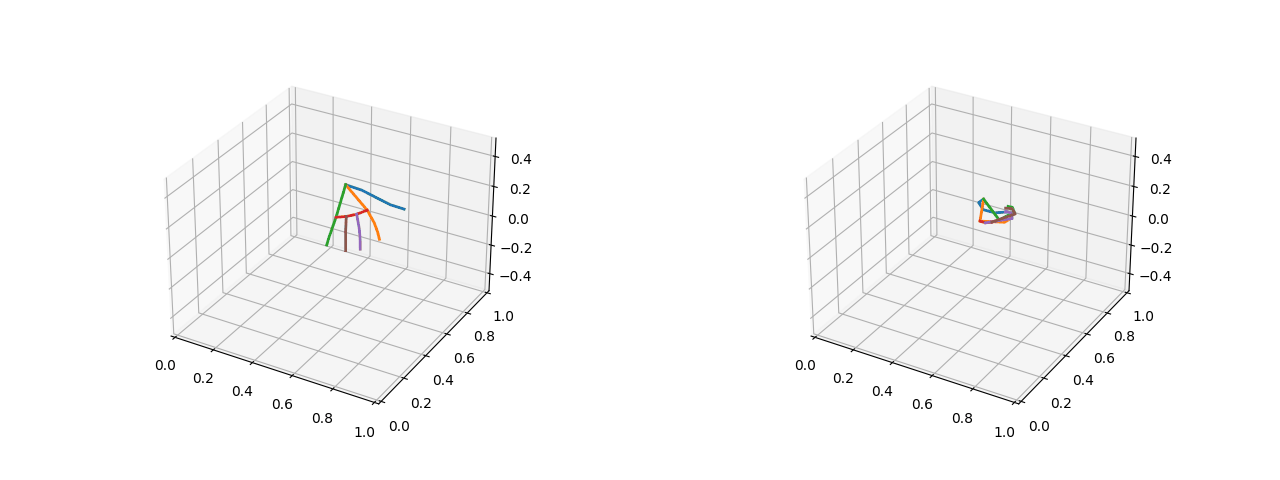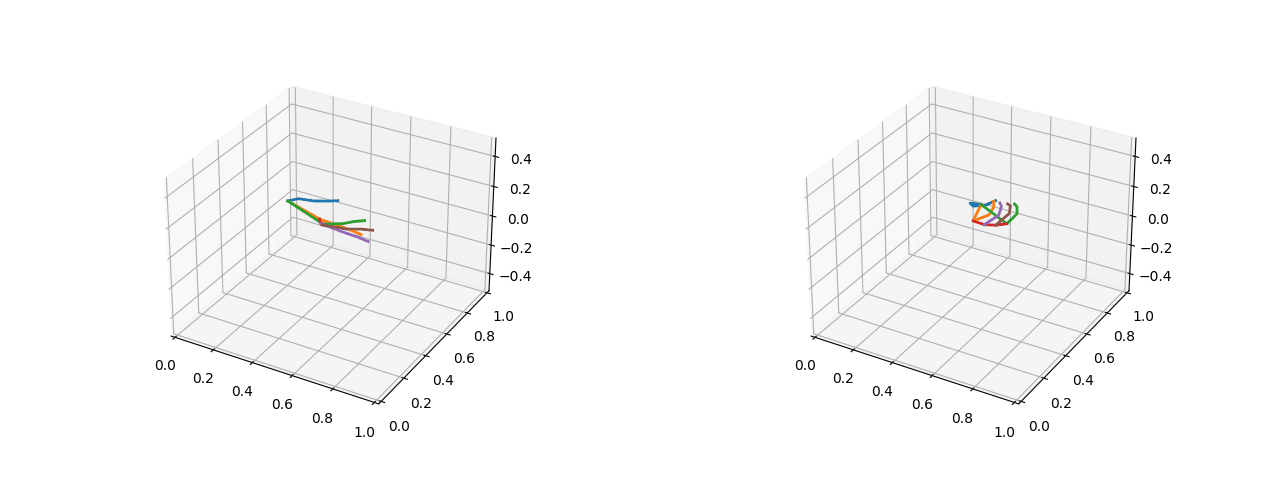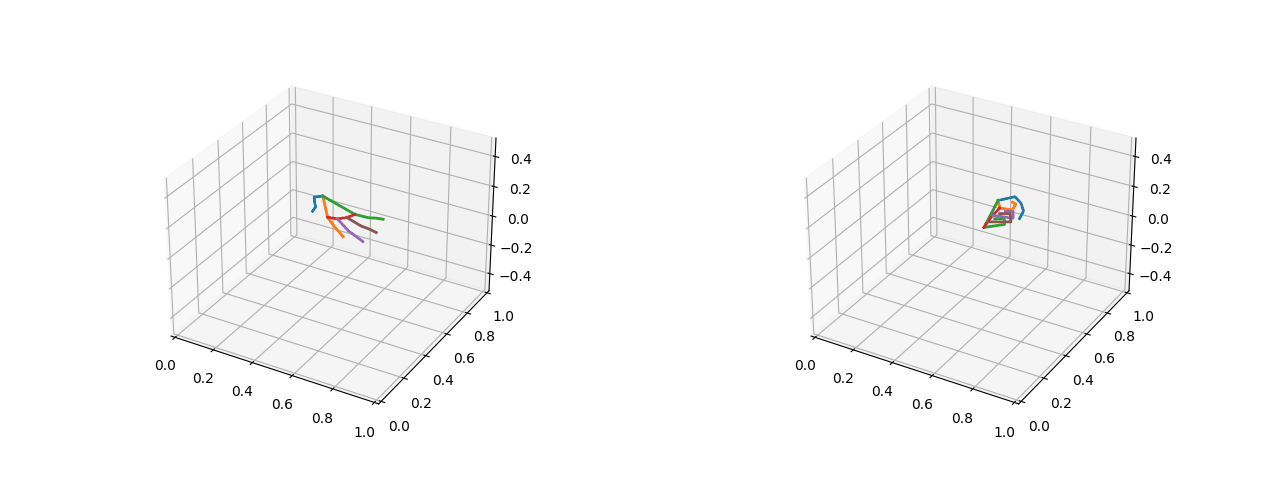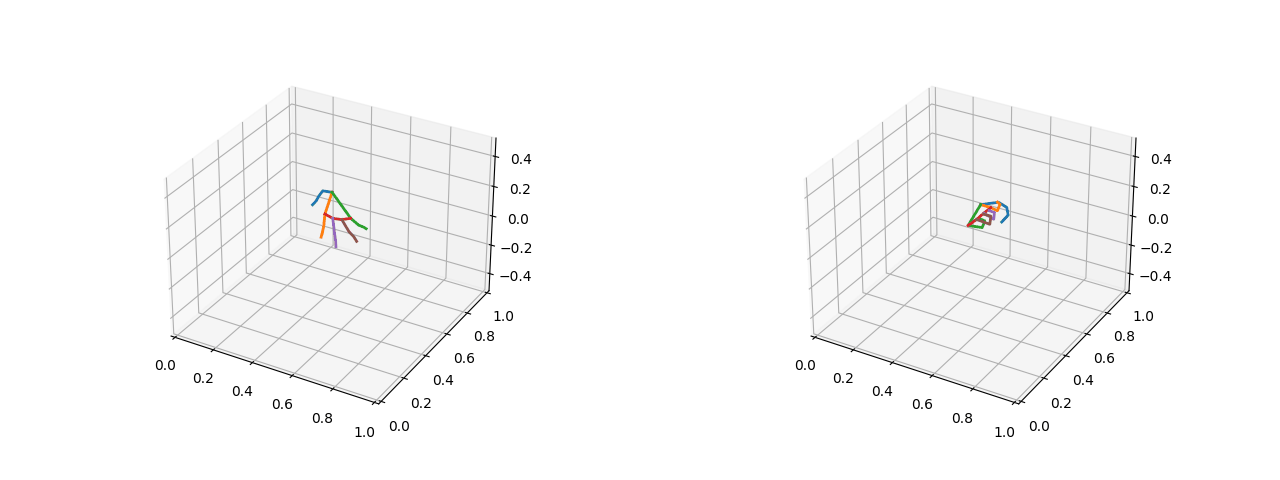
2.1.2 将关键点的绝对坐标转化为相对距离

在计算距离时，利用numpy的广播机制可以一次性得出一个关键点和其余所有关键点两两之间的距离矩阵deal_hand_frame.py：

# 计算手势关键点一点和所有点之间的距离
def calc_dist(p1, p2):
    x = (p1[0]-p2[:,0]) * (p1[0]-p2[:,0])
    y = (p1[1]-p2[:,1]) * (p1[1]-p2[:,1])
    z = (p1[2]-p2[:,2]) * (p1[2]-p2[:,2])
    dist = x + y + z
    return dist

def distance(X):
    dataSets = []
    for hand in X:
        dist_matrix = []
        for i in range(21):
            dist_matrix.append(calc_dist(hand[i], hand))
        # plt.imshow(dist_matrix)
        # plt.pause(0.01)
        # plt.cla()
        dataSets.append(dist_matrix)
    return np.array(dataSets)

除此之外，我们可以将关键点两两之间的距离绘制成距离矩阵，我们可以来可视化这个距离矩阵看看其中是否有有迹可循的特征(说实话看不太出来)(左图为五指张开姿态下的距离矩阵，右图为紧握双拳姿态下的距离矩阵，这两个数据集将作为逻辑斯蒂回归二分类算法的训练集)：

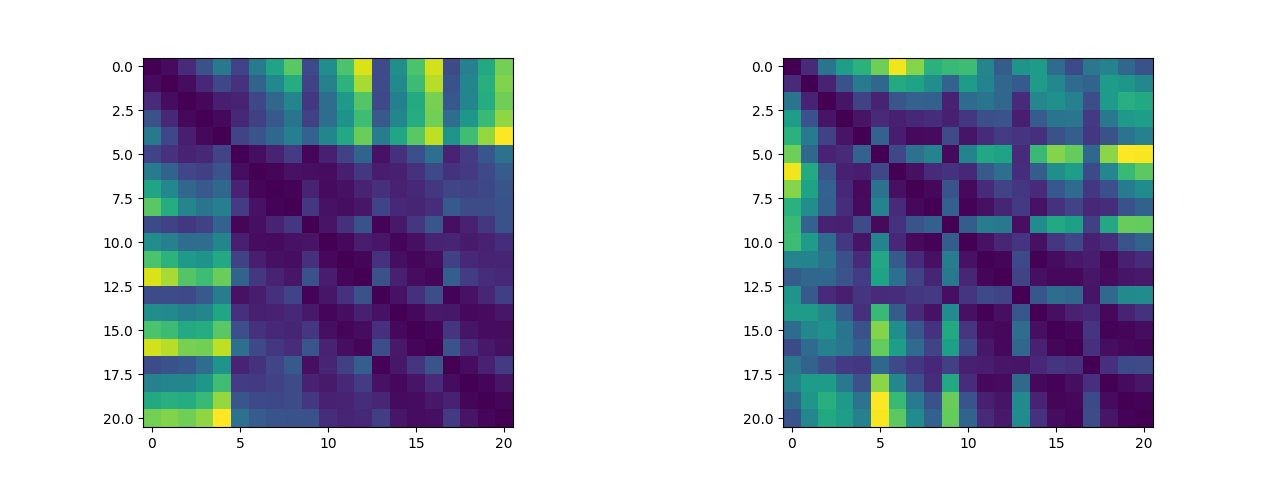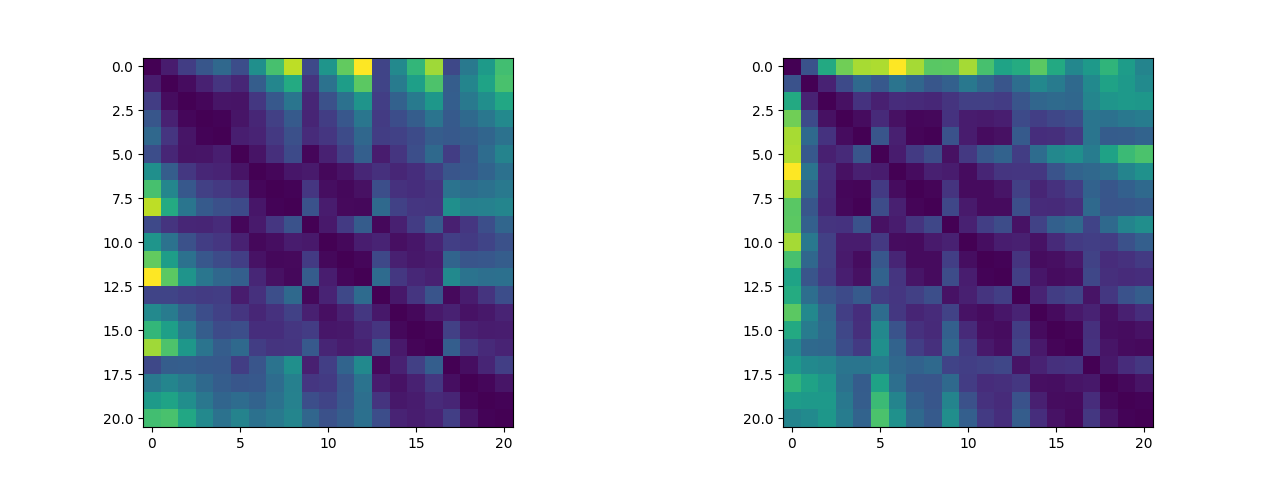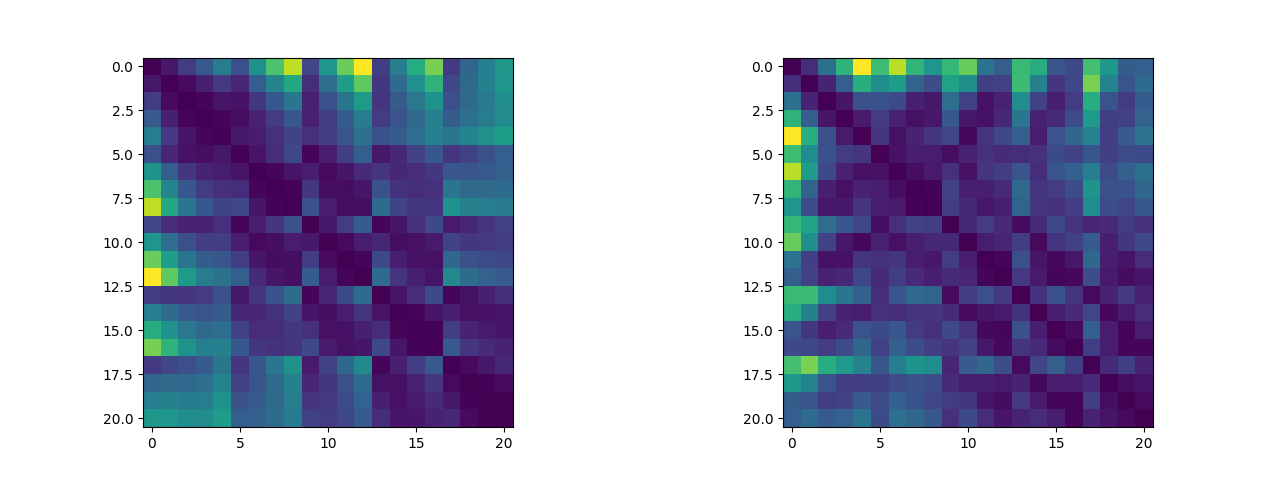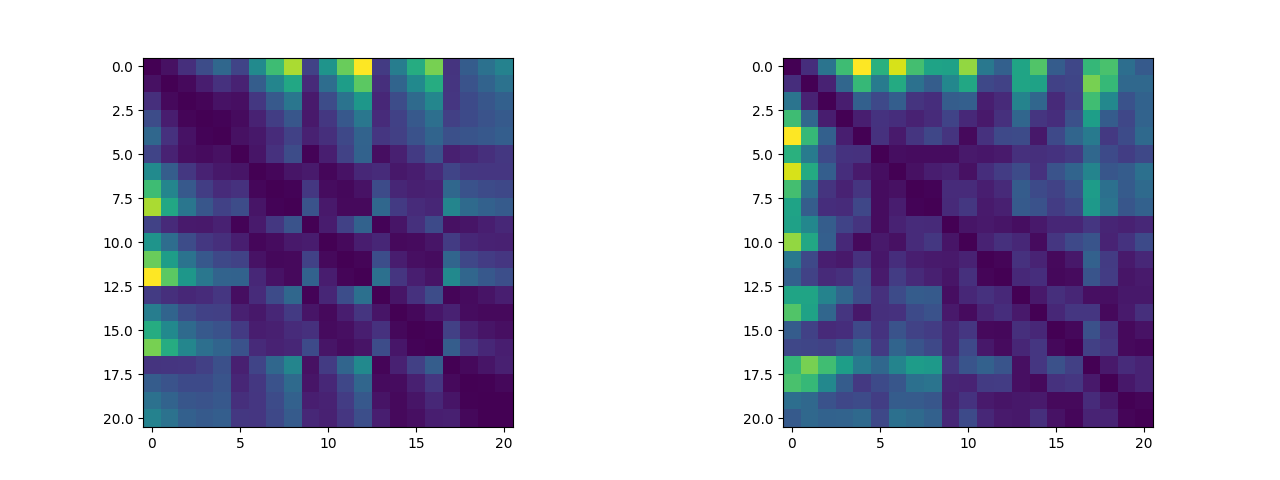
2.2 算法实现

搭建logistic回归算法

logistic算法的原理以及损失函数我已在前两篇【机器学习算法】博客中有了相对详细的介绍，本次实验就不再涉及，感兴趣的小伙伴们可以看看我前两篇撰写的博客。

logistic回归算法代码细节logistic.py：

import sklearn.datasets as datasets # 数据集模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 划分训练集和验证集
import sklearn.metrics # sklearn评估模块
from sklearn.preprocessing import StandardScaler # 标准归一化
from sklearn.metrics import accuracy_score



# 设置超参数
LR= 1e-5         # 学习率
EPOCH = 20000   # 最大迭代次数
BATCH_SIZE = 200  # 批大小


class logistic:
    def __init__(self, X=None, y=None, mode="pretrain"):
        self.X = X
        self.y = y
        # 记录训练损失，准确率
        self.train_loss = []
        self.test_loss = []
        self.train_acc = []
        self.test_acc = []
        # 标准归一化
        self.scaler = StandardScaler()
        # 1. 初始化W参数
        if mode == "pretrain":
            self.W = np.load("../eval_param/Weight.npy")
        else:
            # 随机初始化W参数 初始化参数太大会导致损失可能太大,导致上溢出
            self.W = np.random.rand(X.shape[1]+1, 1) * 0.1 # 均匀分布size = [n,1]范围为[0,1]

    # 将概率转化为预测的类别
    def binary(self, y):
        y = y > 0.5
        return y.astype(int)


    # 二分类sigmoid函数
    def sigmoid(self, x):
        return 1/(1 + np.exp(-x))



    # 二分类交叉熵损失
    def cross_entropy(self, y_true, y_pred):
        # y_pred太接近1会导致后续计算np.log(1 - y_pred) = -inf
        crossEntropy = -np.sum(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)) / (y_true.shape[0])
        return crossEntropy

    # 数据预处理(训练)
    def train_data_process(self):
        self.y = self.y.reshape(-1,1)
        # 划分训练集和验证集,使用sklearn中的方法
        X_train, X_test, y_train, y_test = train_test_split(self.X, self.y, test_size=0.3)
        # 标准归一化
        self.std =  np.std(X_train, axis=0) + 1e-8
        self.mean = np.mean(X_train,axis=0)
        X_train = (X_train - self.mean) / self.std
        X_test = (X_test - self.mean) / self.std
        # 加入偏置
        X_train = np.concatenate((np.ones((X_train.shape[0], 1)), X_train), axis=1)
        X_test = np.concatenate((np.ones((X_test.shape[0], 1)), X_test), axis=1)
        # 每个epoch包含的批数
        NUM_BATCH = X_train.shape[0]//BATCH_SIZE+1
        print('训练集大小:', X_train.shape[0], '验证集大小:', X_test.shape[0])
        return X_train, X_test, y_train, y_test, NUM_BATCH



    def test_data_process(self, X):
        X = X.reshape(1,-1)
        # 标准归一化
        self.std =  np.load('../eval_param/std.npy')
        self.mean = np.load('../eval_param/mean.npy')
        X = (X - self.mean) / self.std
        X = np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)
        return X




    def train(self, LR, EPOCH, BATCH_SIZE):
        X_train, X_test, y_train, y_test, NUM_BATCH = self.train_data_process()
        for i in range(EPOCH):

            # 这部分代码打乱数据集，保证每次小批量迭代更新使用的数据集都有所不同
            # 产生一个长度为m的顺序序列
            index = np.arange(X_train.shape[0])
            # shuffle方法对这个序列进行随机打乱
            np.random.shuffle(index)
            # 打乱
            X_train = X_train[index]
            y_train = y_train[index]
            # 在验证集上评估:
            pred_y_test = self.sigmoid(np.dot(X_test, self.W))
            self.test_loss.append(self.cross_entropy(y_true=y_test, y_pred=pred_y_test))
            self.test_acc.append(accuracy_score(y_true=y_test, y_pred=self.binary(pred_y_test)))
            # 在训练集上评估:
            pred_y_train = self.sigmoid(np.dot(X_train, self.W))
            self.train_loss.append(self.cross_entropy(y_true=y_train, y_pred=pred_y_train))
            self.train_acc.append(accuracy_score(y_true=y_train, y_pred=self.binary(pred_y_train)))

            if i % BATCH_SIZE == 0:
                print("eopch: %d | train loss: %.6f | test loss: %.6f | train acc.:%.4f | test acc.:%.4f" % 
                (i, self.train_loss[i], self.test_loss[i], self.train_acc[i], self.test_acc[i]))

            for batch in range(NUM_BATCH-1):
                # 切片操作获取对应批次训练数据(允许切片超过列表范围)
                X_batch = X_train[batch*BATCH_SIZE: (batch+1)*BATCH_SIZE]
                y_batch = y_train[batch*BATCH_SIZE: (batch+1)*BATCH_SIZE]

                # 2. 求梯度,需要用上多元线性回归对应的损失函数对W求导的导函数
                previous_y = self.sigmoid(np.dot(X_batch, self.W))
                grad = np.dot(X_batch.T, previous_y - y_batch)

                # 加入正则项
                # grad = grad + np.sign(W) # L1正则
                grad = grad + self.W            # L2正则

                # 3. 更新参数,利用梯度下降法的公式
                self.W = self.W - LR * grad


        # 打印最终结果
        for loop in range(32):
            print('===', end='') 
        print("\ntotal iteration is : {}".format(i+1))
        y_hat_train = self.sigmoid(np.dot(X_train, self.W))
        loss_train = self.cross_entropy(y_true=y_train, y_pred=y_hat_train)
        print("train loss:{}".format(loss_train))
        y_hat_test = self.sigmoid(np.dot(X_test, self.W))
        loss_test = self.cross_entropy(y_true=y_test, y_pred=y_hat_test)
        print("test loss:{}".format(loss_test))
        print("train acc.:{}".format(self.train_acc[-1]))
        print("test acc.:{}".format(self.test_acc[-1]))


    def eval(self, X):
        X = self.test_data_process(X)
        y_hat = self.sigmoid(np.dot(X, self.W))
        return y_hat
        

    # 保存权重
    def save(self):
        np.save("./eval_param/Weight.npy", self.W)
        np.save("./eval_param/std.npy", self.std)
        np.save("./eval_param/mean.npy", self.mean)

        np.save("./eval_param/train_loss.npy", self.train_loss)
        np.save("./eval_param/test_loss.npy", self.test_loss)
        np.save("./eval_param/train_acc.npy", self.train_acc)
        np.save("./eval_param.test_acc.npy", self.test_acc)

2.3 训练

import sklearn.datasets as datasets # 数据集模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 划分训练集和验证集
import sklearn.metrics # sklearn评估模块
from sklearn.preprocessing import StandardScaler # 标准归一化
from sklearn.metrics import accuracy_score


import sys;sys.path.append('../')
from logistic import logistic


if __name__ == "__main__":
    # 设置超参数
    LR= 1e-5         # 学习率
    EPOCH = 2000   # 最大迭代次数
    BATCH_SIZE = 200  # 批大小

    # 导入数据集
    X1 = np.load("cloth_dist.npy")
    y1 = np.zeros(X1.shape[0])
    X2 = np.load("stone_dist.npy")
    y2 = np.ones(X1.shape[0])
    X  = np.concatenate((X1,X2), axis=0).reshape(-1,21*21)
    y  = np.concatenate((y1,y2), axis=0)

    model = logistic(X, y, mode="pretrain")

    model.train(LR, EPOCH, BATCH_SIZE)
    model.save()

    idx = 635
    print(model.eval(X[idx,:]), y[idx])

eopch: 0 | train loss: 12.153463 | test loss: 11.694130 | train acc.:0.0571 | test acc.:0.0667
eopch: 200 | train loss: 0.008306 | test loss: 0.007973 | train acc.:0.9986 | test acc.:1.0000
... ...
eopch: 2000 | train loss: 0.000877 | test loss: 0.000713 | train acc.:1.0000 | test acc.:1.0000
================================================================================================
total iteration is : 2000
train loss:0.0008687095801340618
test loss:0.0007078273117643203
train acc.:1.0
test acc.:1.0

loss与acc曲线可视化：

train_loss = np.load("./eval_param/train_loss.npy")
test_loss = np.load("./eval_param/test_loss.npy")
train_acc = np.load("./eval_param/train_acc.npy")
test_acc = np.load("./eval_param/test_acc.npy")

plt.subplot(211)
plt.plot(train_loss[100:], label = 'train loss')
plt.plot(test_loss[100:], label = 'test loss')
plt.xlabel('epoch')
plt.ylabel('CEloss value')
plt.legend()

plt.subplot(212)
plt.plot(train_acc, label = 'train acc')
plt.plot(test_acc, label = 'test acc')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.legend()

可以发现，最终模型在验证集上的测试结果出人意料的好，接下来我们看看模型的泛化性能如何。

2.4 测试

算法测试(嵌入mediapipe手部关键点提取代码中)

只需在手部关键点提取代码下加上这几行代码即可(记得导入自定义的包)：

... ... 
from deal_hand_frame import distance
import sys;sys.path.append('../')
from logistic import logistic
... ...  
      X = distance(keypoint.reshape(1,21,3)).reshape(-1)
        # print(int(model.eval(X)>0.5))
        cls = {0:'cloth', 1:"fist"}
        cv2.putText(image, cls[int(model.eval(X)>0.5)], (200,50), cv2.FONT_HERSHEY_SIMPLEX, 2, (0, 0, 255), 3)
... ...

最终算法基于实时摄像头的识别效果还是非常Robust的：

3. 算法改进

在 2.1.2 中距离矩阵的实现过程以及可视化中不难发现，计算关键点两两之间的距离仍然存在冗余，就比如关键点1和关键点6的距离与关键点6和关键点1的距离是完全相同的，因此当前算法求得的距离矩阵是个对称阵，在后续的改进中，我们可以只选取距离矩阵的上三角区域。

还有就是，关键点自己与自己之间的距离一定是0，因此距离矩阵的主对角线上的维度也可以舍弃。除此之外，手部相邻关节的两个关键点之间的距离现实中也一定是相同的(除非你脱臼了)，因此这些关键点之间的距离上的扰动也只能作为噪声而存在。在后续算法的改进中也可以将这些维度去除。

未完待续。。。