JZ36. 二叉搜索树与双向链表_2021dragon的博客

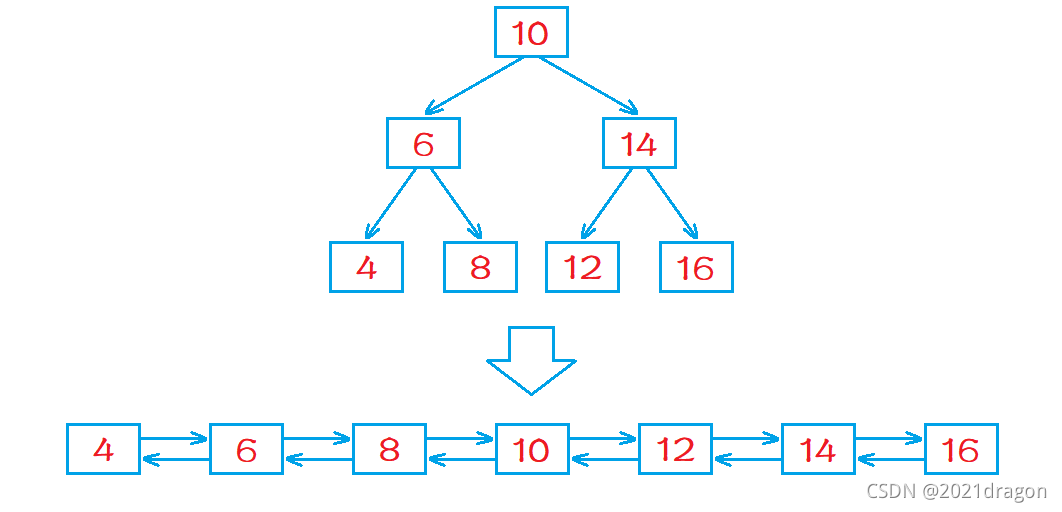
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表，如下图所示：

注意：

1. 要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中结点的左指针需要指向前驱，树中结点的右指针需要指向后继。
2. 返回链表中第一个结点的指针。
3. 函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构。
4. 你不用输出双向链表，程序会根据你的返回值自动打印输出。

示例：
 输入：{10, 6, 14, 4, 8, 12, 16}
 返回值：From left to right：4, 6, 8, 10, 12, 14, 16
     From right to left：16, 14, 12, 10, 8, 6, 4
 说明：输入上图二叉树，返回双向链表的头结点即可。

思路：
因为题目所给二叉树是搜索二叉树，而搜索二叉树的中序遍历就是升序的，所以我们可以按照中序的逻辑进行处理。

既然是双向链表，那么只用一个变量遍历二叉树是显然不够的，在转换过程中至少需
要用到两个变量进行处理：

• cur：标记当前遍历到的结点。
• prev：标记上一次遍历到的结点，即转换成双链表后cur的前驱结点。

此时我们便可以从根结点开始对二叉树进行处理了，若遍历到的cur结点为空，自然无需处理，当遍历到的cur结点不为空时，处理逻辑如下：

1. 先处理cur的左子树。
2. 再处理cur结点。处理时，先让cur的左指针（前驱指针）指向上一次遍历到的结点prev，再让prev的右指针（后继指针）指向结点cur，此时便建立了结点cur和prev之间的双向关系，此后再更新prev的值即可。
3. 最后处理cur的右子树。

而处理cur左右子树的逻辑与处理最初的二叉树的逻辑无异。处理完后，我们只需从根结点开始，一直找其前驱结点，最终便可找到双向链表中的第一个结点进而进行返回。

处理后二叉搜索树各个结点的左右指针指向如下：

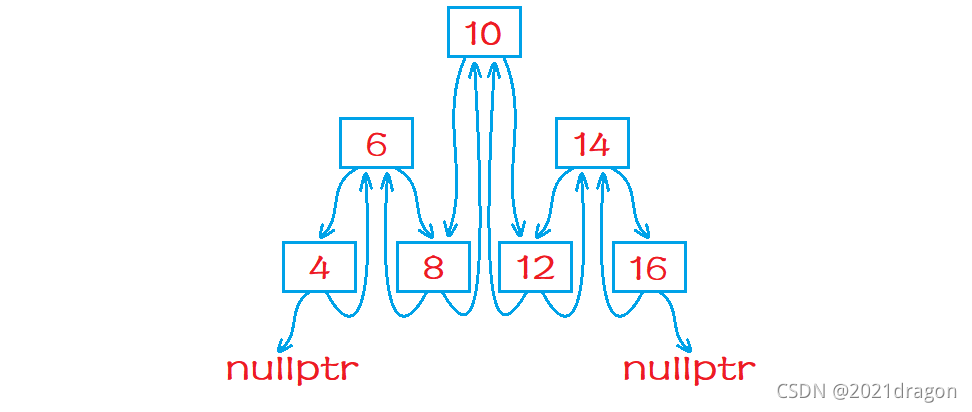
将其“拉直”后实际上就是一个双向链表：

代码如下：

struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
	val(x), left(NULL), right(NULL) {
	}
};
class Solution {
public:
	void Inorder(TreeNode* cur, TreeNode*& prev)
	{
		if (cur == nullptr) //cur为空不做处理
			return;
		//cur不为空，按中序的逻辑进行处理
		Inorder(cur->left, prev); //先处理其左子树
		//再处理cur结点
		cur->left = prev; //cur的左指向其前驱prev
		if (prev) //如果前驱prev不为空，则让前驱指向cur
			prev->right = cur;
		prev = cur; //更新prev
		Inorder(cur->right, prev); //最后处理其右子树
	}
	TreeNode* Convert(TreeNode* pRootOfTree) {
		if (pRootOfTree == nullptr) //空树不做处理
			return nullptr;
		TreeNode* prev = nullptr; //用于标记前驱结点
		Inorder(pRootOfTree, prev); //将搜索二叉树转换成排序的双向链表
		TreeNode* head = pRootOfTree;
		//从根结点一直找前驱即可找到链表中的第一个结点
		while (head->left)
		{
			head = head->left;
		}
		return head; //返回链表中的第一个结点
	}
};

注意事项：

1. 我们在处理cur结点时，都要让cur结点的左指针指向prev，为了处理各个结点时逻辑统一，因此prev的初值最好为nullptr，这样第一个被处理的结点（最后一个左路结点）的左指针便被处理时也能理所当然的指向空了。
2. prev在传参时采用引用传参，因为我们不希望在递归函数在返回时自主改变prev的指向，相反，我们希望cur随着递归函数的返回自主改变cur的指向，从而才能正确遍历二叉树，因此cur在传参时不能采用引用传参。
3. 若想使得转换后的双向链表为循环双向链表，只需在转换后建立链表中首尾结点之间的双向关系即可，从根结点一直往右走即可找到链表中的最后一个结点。