选择排序

选择排序原理

什么是选择排序呢？选择排序，就是在一组乱序的数组arr[n]中，遍历第一遍选择出最小的，与arr[0]交换位置，将最小的数，放到首位，接下第二次遍历，在选择出次小的，放到arr[1]的位置上,然后第三次，第四次…遍历到最大的元素出来，将其放到arr[n]的位置上去。这样这组数据就变得有序了。

选选择排序是不稳定的排序方法。每次第i次遍历查找要执行N-i个单位时间，然后要执行N次，故时间复杂度为o（ n 2 n^{2 } n2），比较适合较小的数列的排序。

思想是：从第一位置开始，逐渐向后，选择后面的无序序列中的最小值放到该位置。简单的来说就是每一次在每一组数中选最大的放到最后或者最前。

算法实现

1、算法描述

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再在剩余的数中选次大的数放到倒数第二个位置，以此类推，直到所有元素均排序完毕。

2、图示

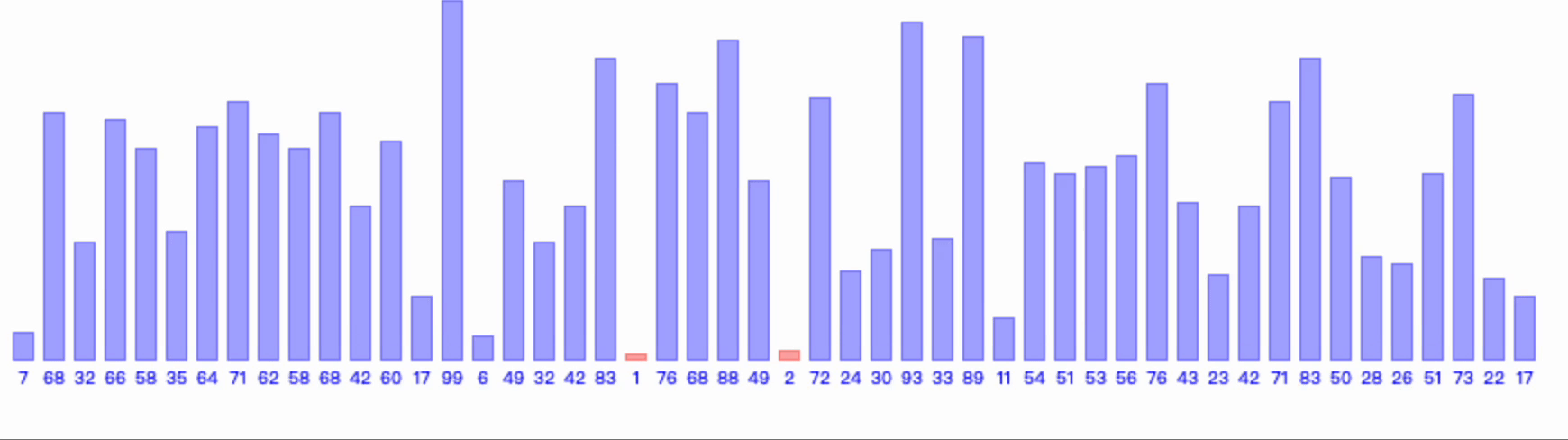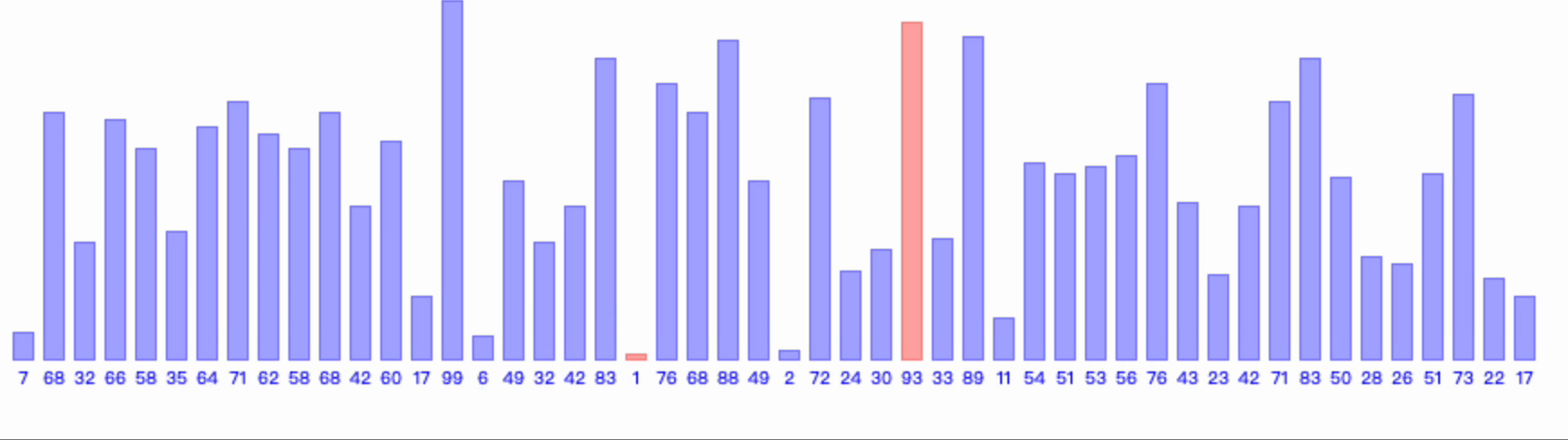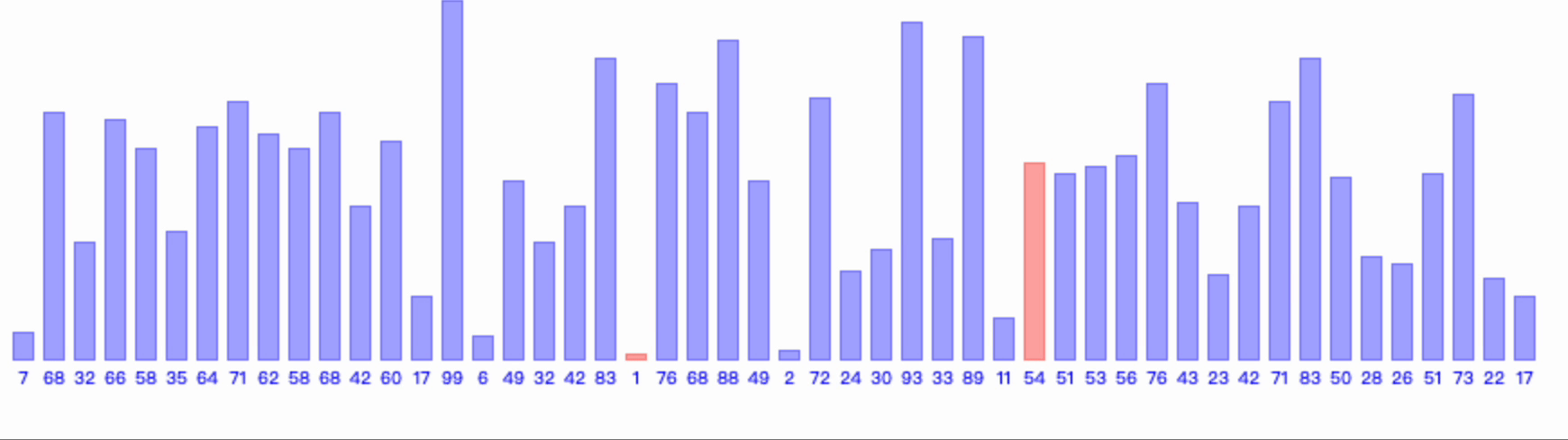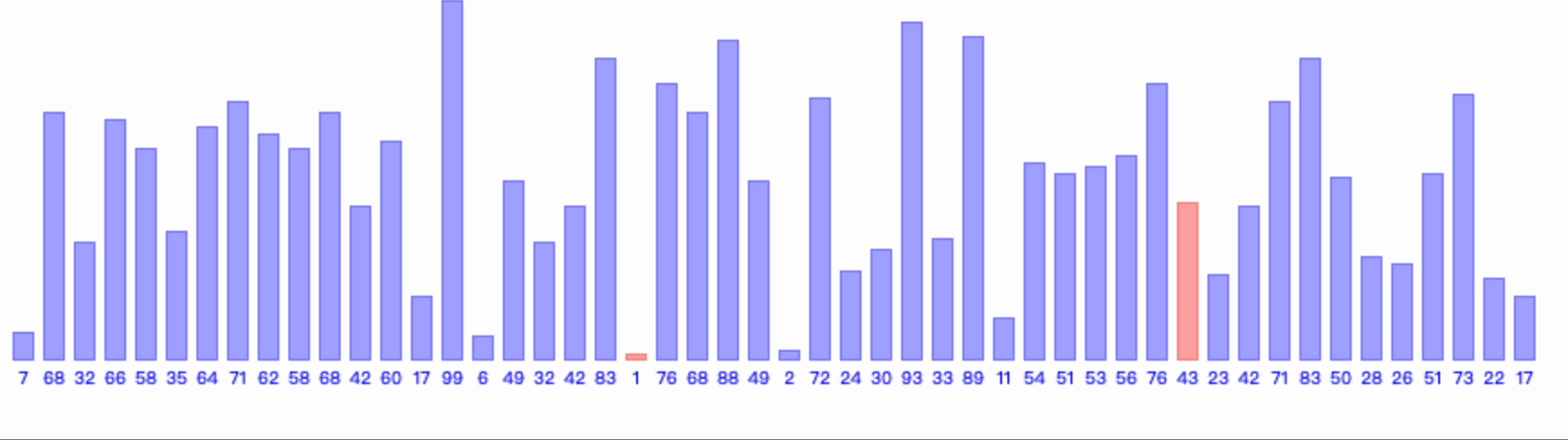
3、算法空间复杂度和时间复杂度
时间复杂度：

• 最坏：o（ n 2 n^{2 } n2）
• 最好：o（ n 2 n^{2} n2）
• 平均：o（ n 2 n^{2 } n2）

空间复杂度（辅助存储）：o（1）
稳定性：不稳定

例题

用选择排序将以下数列按照从小到大的顺序输出：123,45,6,22,99,1,38,41,-6,0

java代码：

public class Test {
    public static void selectSort(int[] arr) {
        if (arr == null || arr.length == 1) return;

            for (int i = 0; i < arr.length - 1; i++) {
                // minIndex是最小元素的索引。
                int min = i;
                // 找到最小元素的索引值，赋给minIndex.
                for (int j = i + 1; j < arr.length; j++) {
                    if (arr[j] < arr[min]) {
                        min = j;
                    }
                }
                // 交换元素
                arr[i] = arr[i] ^ arr[min];
                arr[min] = arr[i] ^ arr[min];
                arr[i]= arr[i] ^ arr[min];

            }
    }


    public static void main(String[] args) {
        int[] arr=new int[]{123,45,6,22,99,1,38,41,-6,0};
        //选择排序
        selectSort(arr);

        System.out.println("选择排序后的结果是:");
        for(int i=0;i<arr.length;i++)
            System.out.print(arr[i]+"\t");
    }

}

堆排序

堆排序原理

堆排序是对于选择排序的优化排序，它利用率了最大（最小）堆顶的数最大（最小）的性质，使得找到一个数组找到最大（最小）的元素的操作不需要像选择排序一样消耗N-i的时间。

堆是一棵顺序存储的完全二叉树。

• 其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。
• 其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。

我们以大根堆为例,我们把堆顶与最后的位置交换,然后其余的元素继续调整建堆,再把堆顶的元素和倒数第二个位置的元素进行交换,直到所有的数有序。

算法实现

1、算法描述
在堆的数据结构中，堆中的最大值总是位于根节点（在优先队列中使用堆的话堆中的最小值位于根节点）。堆中定义以下几种操作：

• 最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
• 创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
• 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

步骤：

1. 创建一个堆 H[0……n-1]；
2. 把堆首（最大值）和堆尾互换；
3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
4. 重复步骤 2，直到堆的尺寸为 1。

2、图示

3、算法空间复杂度和时间复杂度
空间复杂度：

• 最坏：o（ n log ⁡ 2 n n\log _{2}n nlog2​n）
• 最好：o（ n log ⁡ 2 n n\log _{2}n nlog2​n）
• 平均：o（ n log ⁡ 2 n n\log _{2}n nlog2​n）

时间复杂度（辅助存储）：o（ 1 1 1）
稳定性：不稳定

例题

用堆排序将以下数列按照从小到大的顺序输出：
66,13,51,76,81,26,57,69,23

java代码：

public class Test {
    public static void headSort(int[] list) {
        //构造初始堆,从第一个非叶子节点开始调整,左右孩子节点中较大的交换到父节点中
        for (int i = (list.length) / 2 - 1; i >= 0; i--) {
            headAdjust(list, list.length, i);
        }
        //排序，将最大的节点放在堆尾，然后从根节点重新调整
        for (int i = list.length - 1; i >= 1; i--) {
            list[0] = list[0] ^ list[i];
            list[i] = list[0] ^ list[i];
            list[0] = list[0] ^ list[i];
            headAdjust(list, i, 0);
        }
    }

    private static void headAdjust(int[] list, int len, int i) {
        int k = i, temp = list[i], index = 2 * k + 1;
        while (index < len) {
            if (index + 1 < len) {
                if (list[index] < list[index + 1]) {
                    index = index + 1;
                }
            }
            if (list[index] > temp) {
                list[k] = list[index];
                k = index;
                index = 2 * k + 1;
            } else {
                break;
            }
        }
        list[k] = temp;
    }


    public static void main(String[] args) {
        int[] arr=new int[]{66,13,51,76,81,26,57,69,23};
        //堆排序
        headSort(arr);

        System.out.println("堆排序后的结果是:");
        for(int i=0;i<arr.length;i++)
            System.out.print(arr[i]+"\t");
    }

}