在前面，我们简单提及过二叉树的遍历方式，有递归和非递归两个版本的遍历。仔细想一想，不管是递归的，还是非递归的遍历，两种版本的遍历都是需要耗费大量的、额外的空间。比如当我们二叉树的高度有100层，那么递归时，系统就会一直压栈，最坏情况下，一直要压入100次遍历的递归函数，因为此处的空间复杂度是跟这颗二叉树的高度相关的。所以有人就在想，有没有什么方式，能够使这个空间复杂度再压缩一点呢？

前期文章：二叉树的非递归遍历

本期文章源码：GitHub

有，肯定是有的。那就是今天的主题：Morris遍历。这种思想就能使二叉树的遍历，空间复杂度为O(1)。那我们直接开始吧！

一、Morris

在讲解之前，我们来分析一下。为什么遍历二叉树需要压栈？

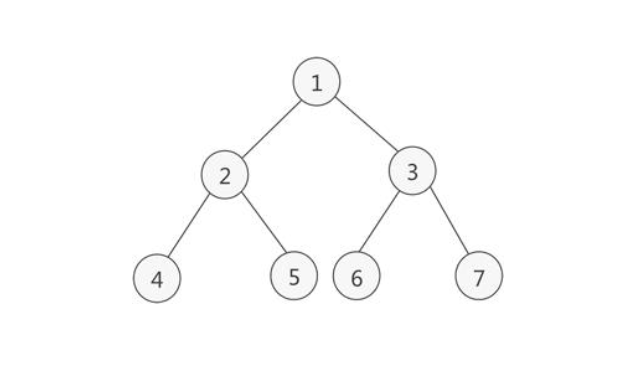
观察上面这颗二叉树，脑补一下。当我们一直往下遍历时，走到值为4的节点，打印输出4后，我该怎么回到2节点？ 每个节点都是只有指向左右孩子的引用，并没有指向父节点的引用。

所以在遍历4节点的时候，会提前将2节点的所有信息，放入栈里面，只有在4节点遍历完成之后，才会弹出栈里的信息（2节点）。然后继续遍历其他的节点。

这也就是为什么遍历二叉树需要压栈的原因。

那么我们就在想啊，有没有种方法，能够不压栈，就能从4节点直接返回到2节点呢？ 那就是利用4节点的右孩子引用。因为4节点是叶子节点，没有左右孩子节点的。 我们将4节点的右孩子引用，指向2节点，这样就能够从4节点直接返回到2节点了。具体的图片如下：

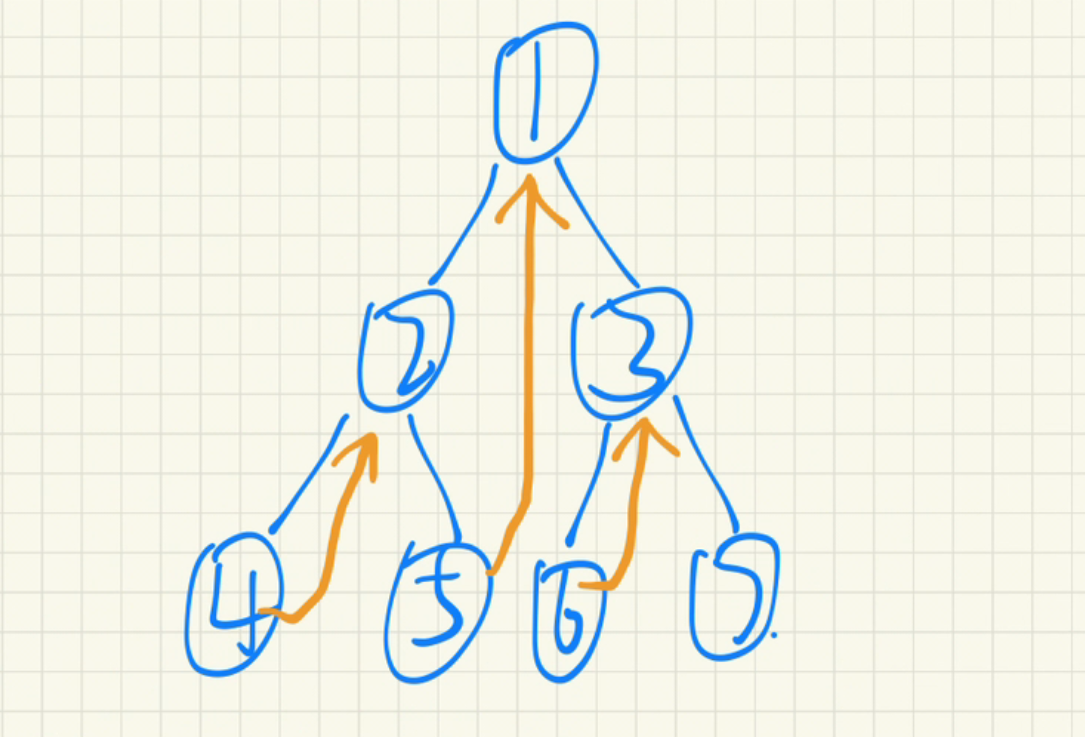
上图橙色的线条，是Morris方法的作用，就是改变某些节点的右孩子引用。然后在具体的遍历过程中，我们将橙色线条擦除即可。保证跟原二叉树一模一样。这就是Morris的思想。 那么问题来了，我们该如何画这些橙色的线条呢？

前提：我们准备两个引用变量：cur和mostRight。 cur表示当前遍历的节点；mostRight表示cur节点左子树中，往右边遍历，第一个没有右孩子的节点。举个例子：上图中cur是1节点，则mostRight就是1节点左子树中，往右下角遍历，5节点就是第一个没有右孩子的节点。

Morris遍历细节：（cur初始化为根结点）

• 如果cur没有左孩子，cur就向右孩子移动。（cur = cur.right）
• 如果cur有左孩子，那就找到cur左子树中，最靠右的节点mostRight：
  • 如果mostRight的右孩子是null，说明是第一次遍历到mostRight。此时让mostRight的右孩子指向cur。
  • 如果mostRight的右孩子是cur，说明是第二次遍历到mostRight。此时让mostRight的右孩子等于null即可。
• 遍历结束条件：cur等于null时

伪代码：

public void morris(Node root) {
    if (root == null) {
        return;
    }
    
    Node cur = root;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight 不等于null) {
        	1、循环找到mostRight节点
            2、判断mustRight的右孩子是否为null
        }
        
        //mostRight等于null时
        cur = cur.right; //向右子树移动
    }
}

上面的伪代码就是大致的框架结构，具体的代码如下：

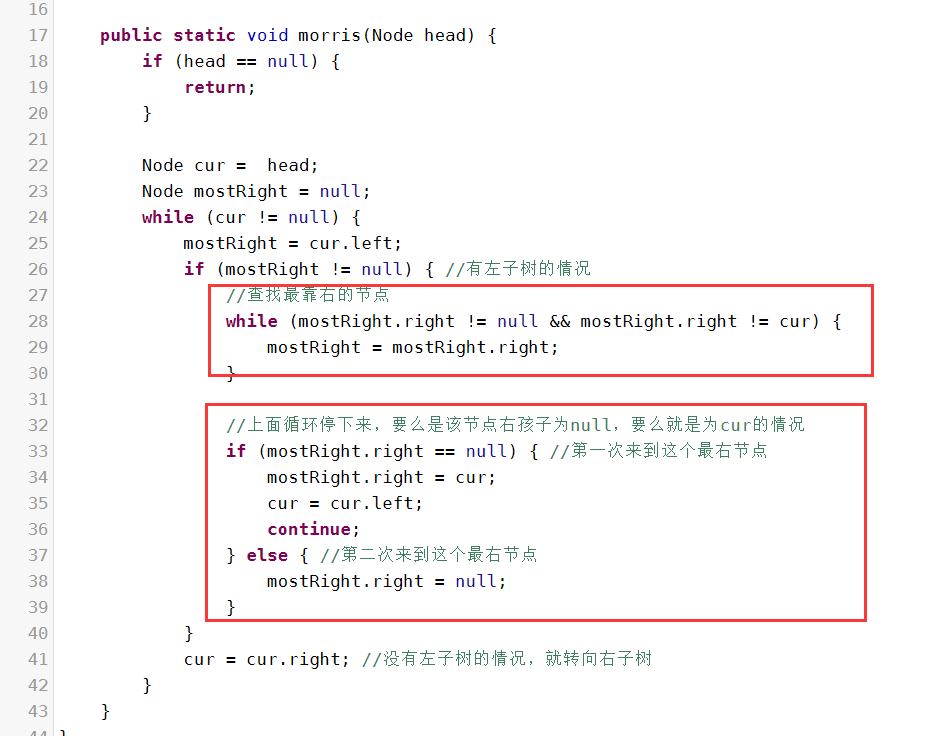
值得注意的是，当第一次遍历到mostRight时，让mostRight的右孩子指向cur之后，cur 再往左子树走，然后应该再写一句continue。让代码继续往cur的左子树继续遍历。

可能有的同学分不清，什么时候是第一次遍历到mostRight，什么是第二次遍历到mostRight。简单点说，第一次就是mostRight的右孩子是null时，此时我们需要将右孩子指向cur；第二次是mostRight的右孩子指向cur的时候，此时我们需要将右孩子重新改回来，改为null。

关于前序、中序、后序遍历，都是在Morris的基础之上，添加printf即可。具体的，请往下看。

二、前序遍历

我们都知道前序遍历的顺序是：头左右。

而Morris改前序遍历，非常简单。记住两个点，你就能独自改前序遍历。

• 如果cur节点没有左孩子，那就打印当前cur的值
• 如果是第一次遍历到mostRight节点，那就打印当前cur的值

就以上两个点，添加到代码里面即可。

其他的代码，原封不动。只添加这两句代码即可完成前序遍历。

三、中序遍历

前序遍历顺序：左头右。

中序跟前序的遍历，这里很相似，也是记住两个点即可：

• 如果cur没有左孩子，直接打印输出cur的值
• 如果mostRight是第二次遍历到，那就打印输出cur的值

跟前序遍历的区别只是mostRight这里，前序是第一次遍历到mostRight就打印cur，中序是第二次遍历到就打印。

当然，这两个printf可以提取出来，写一行即可。这里只是为了让大家清晰地认识到中序遍历。

四、后序遍历（较难）

Morris改后序遍历，稍微有一点点难，因为Morris遍历出来的左右结果，都满足一个规律：当前节点没有左子树，那么只会遍历一次这个节点；当前节点有左子树，那么会有mostRight节点会返回到cur节点，也就是说有左孩子的节点，会遍历两次。

后序遍历是每个节点，遍历到第3次的时候，才打印输出，现在可好，Morris遍历最多只能遍历到2次，那该如何是好？？？

不急，我们来看一张图：

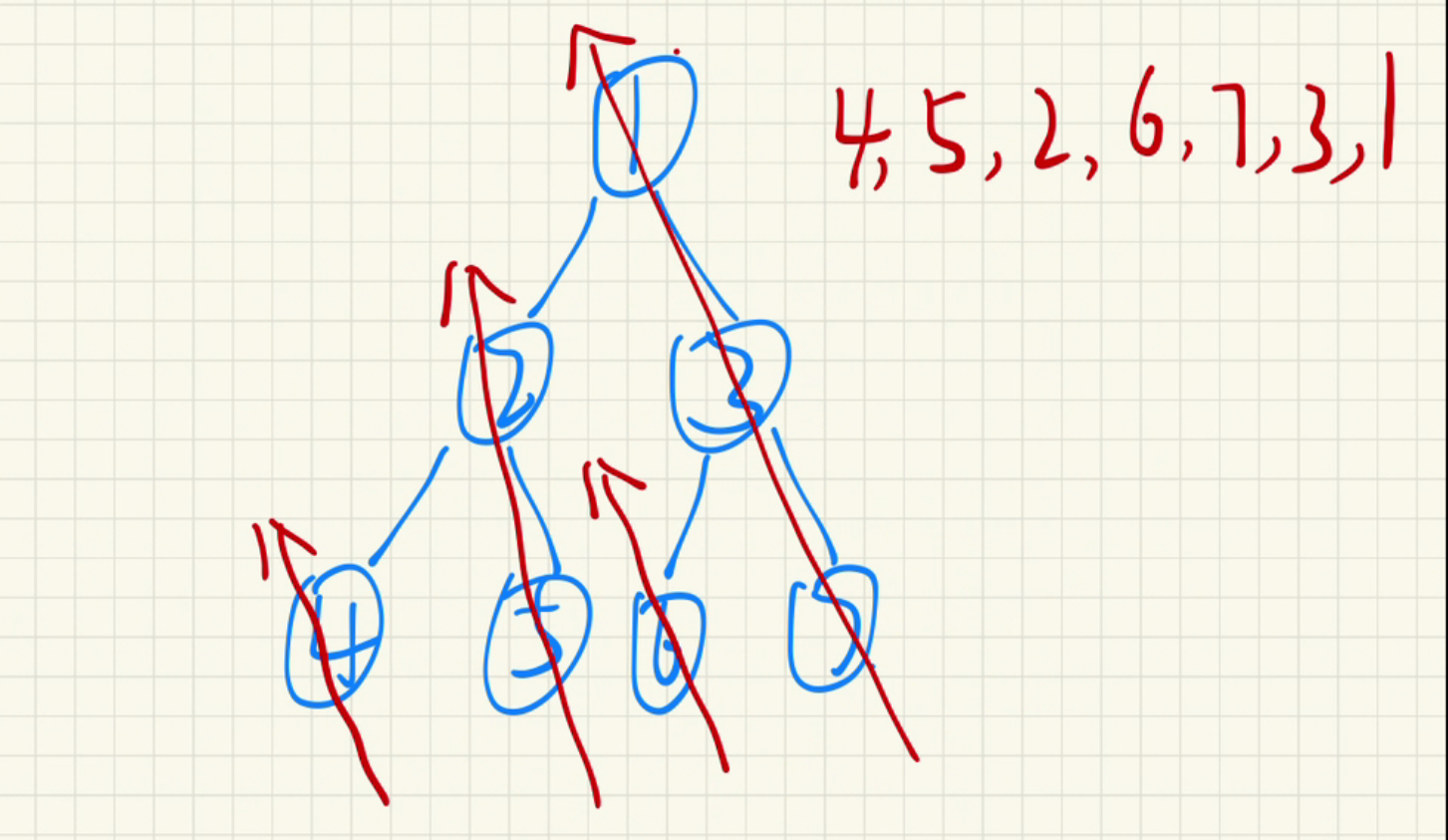
不难发现，红色的数值就是后序遍历的结果。对比下左边的二叉树，红色线条的指向，从左到右，从下到上的打印顺序，竟然跟后序遍历的结果是一样的。

那我们就以这个为切入点，当遍历cur的时候，我们就可以打印cur左子树的最靠右的那一排的节点。比如cur等于1节点的时候，我们就可以打印2、5节点。

要满足从下到上的打印顺序，最容易想到的就是搞一个栈，压栈进行，然后再依次弹出栈并打印。这样的话，空间复杂度就不是O(1)了。 大家是否还记得逆序单链表？我们将那一排的节点，进行逆序，然后打印输出之后，再逆序回来即可。

//逆序那一排节点
public Node reverseList(Node node) {
    Node pre = null;
    Node next = null;
    while (node != null) {
        next = node.right; //逆序右子树那一排节点
        node.right = pre;
        pre = node;
        node = next;
    }
    return pre;
}

逆序完成之后，打印输出即可，然后在逆序回来，保持原来的状态

public void printList(Node node) {
    Node newHead = reverseList(node); //逆序
    node = newHead; //先保存newHead，等会逆序
    
    while (newHead != null) {
        System.out.print(newHead.val + " ");
        newHead = newHead.right; //向右子树走
    }
    reverseList(node); //逆序回来，保持原状态
}

上面两个方法，就能实现打印行为。现在的问题是，怎么进行调用？？？

Morris遍历，有的节点会遍历到一次，而有的节点会遍历到两次。牢牢抓住这两种情况，Morris遍历就简单了。

这里的后序遍历，还是跟前序和中序差不多，只是打印函数，我们在第二次遍历到mostRight调用即可。

比如：在上图中，第二次遍历到mostRight等于4节点时，我们就调用打印函数，传递的参数是cur的左孩子。再比如：第二次遍历到mostRight等于5节点时，此时调用printList（cur.left），此时的cur是1节点。

看代码更清晰：

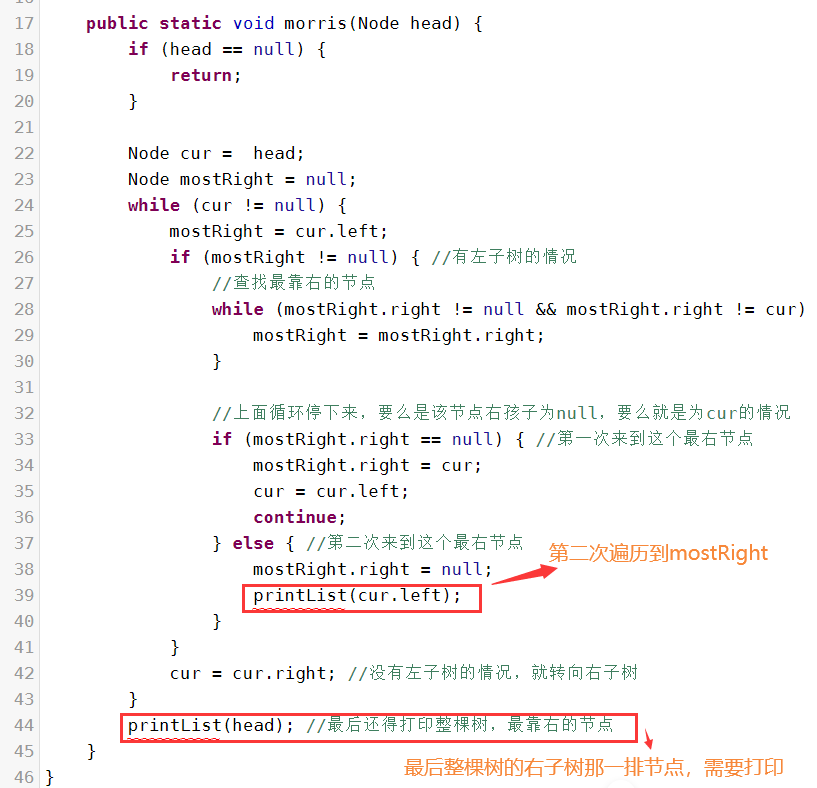
最后切记，当24行~43行的循环结束后，还剩下整棵树的最靠右的那一排节点没有打印（对应上图就是：1、3、7节点还没打印），要单独调用打印函数，传递根结点即可。

好啦，以上全部就是Morris遍历二叉树的全部情况，牢牢抓住cur节点有没有左子树的情况，应该就能很好理解了。