在建立好灰色模型后，首先要进行模型的检验，以检验模型的效果。一般有三种检验方法：相对残差检验、关联度检验、后验差检验。当三种检验全部通过时，表明模型的效果较好，才可以使用模型进行后续的预测；否则，将要对模型进行残差修正，直到三种检验均通过为止。
这篇文章就着重阐述一下三种检验~
一、检验准则
下面就不详细阐述各检验的基本原理了，重点说一下各检验的评判准则。
1.相对残差检验（根据自己的要求与题意任选一个要求进行衡量即可）
（1）最严格的要求：（i）<0.005 其中
（i）为相对误差序列，这个不等式表示当相对误差序列中的元素应都小于0.005时，通过相对残差检验。
（2）较宽泛的要求：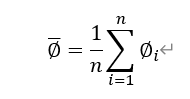 
其中
表示相对误差序列中元素的均值。
给定a，当
，当不等式成立时，称模型为合理模型。
一般a取0.01、0.05、0.1，分别对应优秀、合格、勉强通过。
2.关联度检验
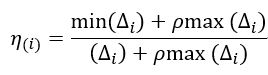
其中 当
，关联度大于0.6时，检验通过。
3.后验误差
方差比C、小误差概率：
根据P与C的取值，有对应好、合格、勉强合格、不合格的模型评价结果。
二、例题
题目：利用GM（1,1） 对以下数据进行预测，并对得到的模型进行三种检验。
利用GM（1,1）进行预测得到对应的结果：
分别对预测进行上述三种检验：（注：此处的结果与下方代码的输出结果对应）
1.相对残差检验
此处输出的为相对残差序列，发现相对残差序列都小于0.5%，因此认为模型的精确度高。
若每个序列都小于0.5%，就不用考虑相对平均误差了，因为当严格检验通过时，较宽泛的检验一定也通过。（因此此题只看严格检验的结果就足够了，下面的较宽泛检验可删去，但是为了让大家可以将这个检验应用到不同的情况，进行了宽泛检验的讲解）。
当严格检验不通过时，可以考虑较宽泛的检验，从而对模型进行检验（这里的思想类似于假设检验里a的选取，如果对模型的要求高就对其进行严格检验，若要求不是太高，可降低标准，以使模型通过检验。），得到如下结果：
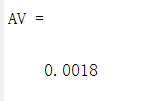
可以得到相对平均误差为0.0018，小于0.01.因此通过相对残差检验。
2.关联度分析
得到平均关联系数:
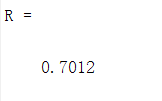
R大于0.6，因此表明预测序列与原始序列的关联度较强，通过关联度检验。
3.后验差检验
得到方差比为1.8879%，小误差概率为100%，根据判断准则发现，C<0.35,同时P>0.95,因此说明模型较好，认为通过后验差检验。
综上，三种检验均通过，因此可以使用此模型进行后续的预测与操作。
以上就是这次分享的内容，后期会陆续更新统计算法、机器学习、R软件等相关内容，感兴趣的小可爱，关注一波~
残差检验、关联度检验、后验差检验matlab代码如下：
CA=abs(XY-X0) ; %残差数列，X0为原始序列，XY为预测序列
Theta=CA ; %残差检验 绝对误差序列
XD_Theta= CA ./ X0 %残差检验 相对误差序列
AV=mean(XD_Theta) % 残差数列平均值
R_k=(min(Theta)+0.5*max(Theta))./(Theta+0.5*max(Theta)) ;% P=0.5
R=sum(R_k)/length(R_k) %关联度
GD=mean(CA); %绝对残差均值
Temp0=(CA-GD).^2 ;
Temp1=sum(Temp0)/length(CA);
S2=sqrt(Temp1) ; %绝对误差序列的标准差
%----------
AV_0=mean(X0); % 原始序列平均值
Temp_0=(X0-AV_0).^2 ;
Temp_1=sum(Temp_0)/length(CA);
S1=sqrt(Temp_1) ; %原始序列的标准差
TempC=S2/S1*100; %方差比
C=strcat(num2str(TempC),'%') %后验差检验 %方差比
%----------
Delta=abs(CA-AV);
SS=0.675*S1 ;
elta=abs(CA-AV) ;
TempN=find(Delta<=SS);
N1=length(TempN);
N2=length(CA);
TempP=N1/N2*100;
P=strcat(num2str(TempP),'%') %后验差检验 %计算小误差概率