【集成学习系列教程1】AdaBoost原理及sklearn应用_Juicy B的博客

1 Boosting方法

1.1 引言

“团结就是力量”、“众人拾柴火焰高”，“三个臭皮匠，顶个诸葛亮”。小时候我们可能不能完全理解这些话的意思，但是随着年龄的增长，我们渐渐体会到了团队合作的重要性，也渐渐加深了对这些话的理解。非常幸运的是，有很多科学家参透了这些道理，并将它们应用到了机器学习领域。他们发现：将多个预测准确率不怎么高的基础机器学习模型结合成一个混合的模型，往往可以取得更高的准确率。他们将这些表现较差的基础机器学习模型称为“weak learner“（弱学习器）”，将这个表现较好的混合模型称为"strong learner"（强学习器）。将弱学习器提升为强学习器的方法有很多，其中一种称为 Boosting。在这一章中，我们将对该方法进行详细介绍，领略它的神奇之处。

1.2 Boosting基本思想及工作过程

这里将举一个非常简单的例子来对Boosting的基本思想和工作过程做一个简要的介绍。以一个二分类任务为例子。假设有如下数据集，它由3个小的子数据集组成：
D = { ( X 1 , y 1 ) , ( X 2 , y 2 ) , ( X 3 , y 3 ) } D= \{ (X_1,y_1),(X_2,y_2),(X_3,y_3)\} D={(X1​,y1​),(X2​,y2​),(X3​,y3​)}
其中 X i X_i Xi​ 里面由多个样本，数据集的标签 y i ∈ { 0 , 1 } y_i\in\{0,1\} yi​∈{0,1} 。我们为这三个子数据及都分配一个相同的权重，将这三个权重所对应的分布记为 D i s t 1 Dist_1 Dist1​，则：
D i s t 0 : w 1 = w 2 = w 3 = 1 3 Dist_0:w_1=w_2=w_3=\frac{1}{3} Dist0​:w1​=w2​=w3​=31​
此时有一个弱分类器 h 1 h_1 h1​，它正确预测了来自 X 2 X_2 X2​ 和 X 3 X_3 X3​ 的样本，但是却错误地预测了来自 X 1 X_1 X1​ 的样本，则它的分类错误率为 1 / 3 1/3 1/3。由于Boosting 的基本思想是不断纠正前一个弱分类器的错误，所以在训练完 h 1 h_1 h1​后，它会更加关注上一轮分错的子数据集 X 1 X_1 X1​，为 X 1 X_1 X1​ 赋予了更大的权重，同时降低了 X 2 X_2 X2​ 和 X 3 X_3 X3​ 的权重。假设此时产生的新分布如下：
D i s t 1 : w 1 = 1 2 , w 2 = 1 4 , w 3 = 1 4 Dist_1:w_1=\frac{1}{2},w_2=\frac{1}{4},w_3=\frac{1}{4} Dist1​:w1​=21​,w2​=41​,w3​=41​
在 D i s t 1 Dist_1 Dist1​ 的基础上，来了一个新的弱分类器 h 2 h_2 h2​。由于上一轮加大了子数据集 X 1 X_1 X1​的权重 w 1 w_1 w1​ ，所以它会更加关注 X 1 X_1 X1​，并减少了在 X 1 X_1 X1​ 上的分类错误，同时也正确预测了来自 X 3 X_3 X3​ 的样本，但是却非常遗憾地预测错了来自 X 2 X_2 X2​ 的样本。不过不要紧，结合 h 1 h_1 h1​和 h 2 h_2 h2​，我们已经可以得到一个在 X 1 X_1 X1​和 X 3 X_3 X3​上的表现均较好的集成分类器 H 2 H_2 H2​。由于 h 2 h_2 h2​ 在 X 2 X_2 X2​ 上表现不好，所以Boosting加大了 X 2 X_2 X2​的权重，假设此时产生了一个新的分布如下：
D i s t 2 : w 1 = 1 4 , w 2 = 1 2 , w 3 = 1 4 Dist_2:w_1=\frac{1}{4},w_2=\frac{1}{2},w_3=\frac{1}{4} Dist2​:w1​=41​,w2​=21​,w3​=41​
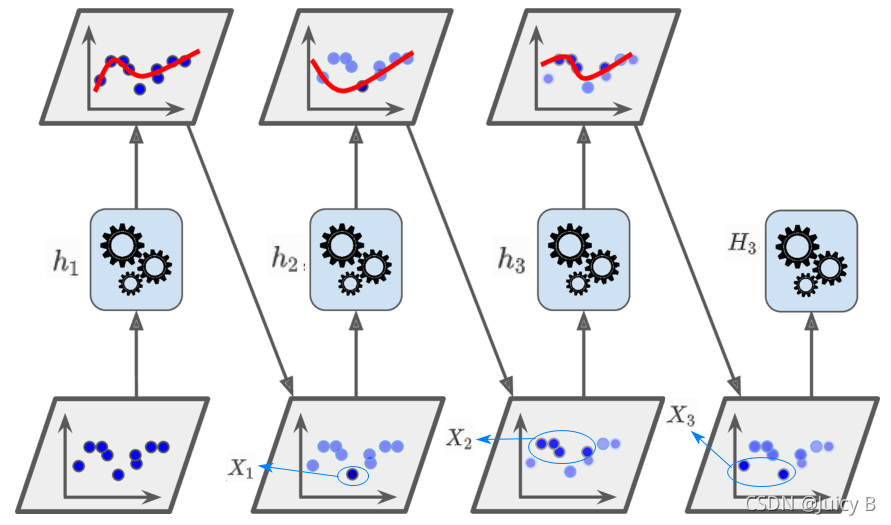
在此基础上，又来了一个新的分类器 h 3 h_3 h3​，它更加关注来自 X 2 X_2 X2​ 的样本，加强了在 X 2 X_2 X2​ 的准确率。这样一来，结合 h 1 h_1 h1​ , h 2 h_2 h2​, h 3 h_3 h3​，我们就可以进一步得到一个在 X 1 X_1 X1​， X 2 X_2 X2​和 X 3 X_3 X3​ 上的分类错误率均较低的较完美的集成分类器 H 3 H_3 H3​。这就是Boosting的工作过程。

上述过程可以用下图表示：

1.3 AdaBoost分类算法

上面对Boosting的工作过程和基本思想进行了简要的介绍。需要注意的是，Boosting代表的是一类算法，它由多种算法组成。其中最著名的算法是AdaBoost，而AdaBoost既可以用于分类任务，也可以用于回归任务。下面就将对如何运用AdaBoost算法完成分类任务的过程做详细的介绍。

1.3.1 解决二分类问题

这一小节将对AdaBoost完成二分类问题的具体步骤进行介绍。

假设有一个如下的二分类的数据集，它由 m m m 个样本组成：
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D= \{ (\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),...,(\boldsymbol x_m,y_m)\} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)}
其中， x i ∈ R d \boldsymbol x_i\in\mathbb{R}^d xi​∈Rd（每一个样本数据有 d d d 个特征）， y i ∈ { − 1 , + 1 } y_i\in\{-1,+1\} yi​∈{−1,+1} 。AdaBoost算法的具体步骤如下：

1. 初始化权重。记初始状态下的数据集样本分布为 D i s t 1 Dist_1 Dist1​，对每一个样本 x i \boldsymbol x_i xi​的权重均初始化为 1 / m 1/m 1/m，则 D i s t 1 ( x i ) = 1 / m Dist_1(\boldsymbol x_i)=1/m Dist1​(xi​)=1/m。 D i s t 1 Dist_1 Dist1​分布用于第一个弱分类器 h 1 h_1 h1​的训练；

2. 循环进行 T T T 轮迭代，记每一轮迭代中弱分类器的编号为 t t t，且 t ∈ { 1 , 2 , 3 , . . . , T } t \in \{1,2,3,...,T\} t∈{1,2,3,...,T}。以该步骤作为循环体，循环体中的步骤进一步细分为：

   1. 在样本分布为 D i s t t ( x ) Dist_t(\boldsymbol x) Distt​(x)的基础上，在数据集 D D D上训练弱分类器 h t h_t ht​；

   2. 求出 h t h_t ht​的分类错误率 ϵ t \epsilon_t ϵt​，计算公式为：
      ϵ t = P x ～ D i s t 0 ( h t ( x ) ≠ f ( x ) ) \epsilon_t=P_{\boldsymbol x ～ Dist_0}\bold(h_t(\boldsymbol x) ≠ f(\boldsymbol x)\bold) ϵt​=Px～Dist0​​(ht​(x)​=f(x))
      其中， h t ( x ) ∈ { − 1 , 1 } h_t(\boldsymbol x )\in\{-1,1\} ht​(x)∈{−1,1}，表示弱分类器 h t h_t ht​对样本 x \boldsymbol x x的预测结果， f ( x ) f(\boldsymbol x) f(x)表示样本 x \boldsymbol x x的标签；

   3. 对 ϵ t \epsilon_t ϵt​进行判断，如果 ϵ t \epsilon_t ϵt​的值大于 0.5 0.5 0.5，则选择丢弃弱分类器 h t h_t ht​，返回到步骤1；如果 ϵ t \epsilon_t ϵt​的值小于 0.5 0.5 0.5，则继续进行下面的步骤（由于这是个二分类问题，所以在随机猜测的情况下对样本的分类错误率的期望为 0.5 0.5 0.5，若此时弱分类器 h t h_t ht​的预测准确率大于 0.5 0.5 0.5，说明其分类效果比随机猜测效果还差，应该将其丢弃）；

   4. 根据上一步求得的分类错误率 ϵ t \epsilon_t ϵt​，求得弱分类器 h t h_t ht​所对应的权重为：
      w t = 1 2 l n ( 1 − ϵ t ϵ t ) w_t=\frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t}) wt​=21​ln(ϵt​1−ϵt​​)
      也就是说， h t h_t ht​ 的分类错误率越低，正确率越高，所对应的权重也越大； h t h_t ht​ 的分类错误率越高，正确率越低，所对应的权重也越小；

   5. 根据上面求出的权重 w t w_t wt​对数据集样本的分布权重进行更新，计算公式为：
      KaTeX parse error: Unknown column alignment: 1 at position 82: …\{\begin{array}1̲ e^{-w_t}, \qua…
      其中， Z t Z_t Zt​为归一化因子，它使得$ Dist_{t+1} $可以满足分布条件，计算公式为：
      Z t = E x ～ D i s t t ( x ) [ e − f ( x ) H t ( x ) ) ] E x ～ D i s t t ( x ) [ e − f ( x ) H t − 1 ( x ) ) ] Z_t = \frac{\mathbb E_{\boldsymbol x～Dist_t(\boldsymbol x)}[e^{-f(\boldsymbol x)H_t(\boldsymbol x))}]}{\mathbb E_{\boldsymbol x～Dist_t(\boldsymbol x)}[e^{-f(\boldsymbol x)H_{t-1}(\boldsymbol x))}]} Zt​=Ex～Distt​(x)​[e−f(x)Ht−1​(x))]Ex～Distt​(x)​[e−f(x)Ht​(x))]​
      由 D i s t t + 1 Dist_{t+1} Distt+1​的计算公式可以看出，对于 h t h_t ht​分错的样本，会增大样本其权重，且 h t h_t ht​的分类准确率越高，对分错样本所加的权重也越大；而对于 h t h_t ht​分对的样本，则相应地减小权重；

   6. 在上述步骤的基础上，训练下一轮中的弱分类器 h t + 1 h_{t+1} ht+1​，理想弱分类器为：

      h t + 1 ( x ) = arg ⁡ min ⁡ h   E x ～ D i s t t + 1 [ I ( f ( x ) ≠ h ( x ) ) ] h_{t+1}(\boldsymbol x)= \mathop{\arg\min}_h\,\mathbb E_{\boldsymbol x～Dist_{t+1}}[\mathbb I \bold(f(\boldsymbol x)\neq h(\boldsymbol x) \bold)] ht+1​(x)=argminh​Ex～Distt+1​​[I(f(x)​=h(x))]
      也就是说，新的弱分类器 h t + 1 ( x ) h_{t+1}(\boldsymbol x) ht+1​(x)的目标是：在更新后的分布 D i s t t + 1 Dist_{t+1} Distt+1​的基础上，努力减小分类错误，使得它可以尽量纠正前一个弱分类器所造成的错误；

   7. 令 t : = t + 1 t := t+1 t:=t+1，回到循环体中的步骤1。

3. 结束 T T T轮迭代，最终得到强分类器如下：
   H ( x ) = s i g n ( ∑ t = 1 T w t h t ( x ) ) H(\boldsymbol x)=sign\bold (\sum_{t=1}^Tw_th_t(\boldsymbol x)\bold) H(x)=sign(t=1∑T​wt​ht​(x))
   其中 s i g n ( x ) sign(x) sign(x)表示符号函数：
   s i g n ( x ) = { − 1 , x < 0 0 , x = 0 1 , x > 0 sign(x)=\left\{ \begin{aligned} -1, \quad x < 0\\ 0,\quad x=0\\ 1, \quad x>0 \end{aligned}\right. sign(x)=⎩⎪⎨⎪⎧​−1,x<00,x=01,x>0​
   这里需要注意：AdaBoost算法中引入了正则化，通过一个称为“学习率”的参数对弱分类器的权重大小进行控制，即：
   H t ( x ) = H t − 1 ( x ) + η w t h t ( x ) H_t(\boldsymbol x)=H_{t-1}(\boldsymbol x)+\eta w_th_t(\boldsymbol x) Ht​(x)=Ht−1​(x)+ηwt​ht​(x)
   这个参数非常重要，在实例3中会重点介绍到该参数的使用。

通过如上步骤，就完成了AdaBoost算法的全过程。

1.3.2 解决多分类问题

前面介绍了如何使用AdaBoost解决二分类问题。下面将介绍如何对AdaBoost进行扩展，使得它可以用于多分类任务。

1.3.2.1 SAMME算法

SAMME算法在AdaBoost算法的基础上做了如下两点改进：

1. 使用多分类学习器代替二分类学习器作为基学习器；

2. 对AdaBoost中弱分类器权重的计算方式进行修改（其他步骤保持不变）。

   • 原来的计算公式为：

   w t = 1 2 l n ( 1 − ϵ t ϵ t ) w_t=\frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t}) wt​=21​ln(ϵt​1−ϵt​​)

   该函数的曲线图如下：
   

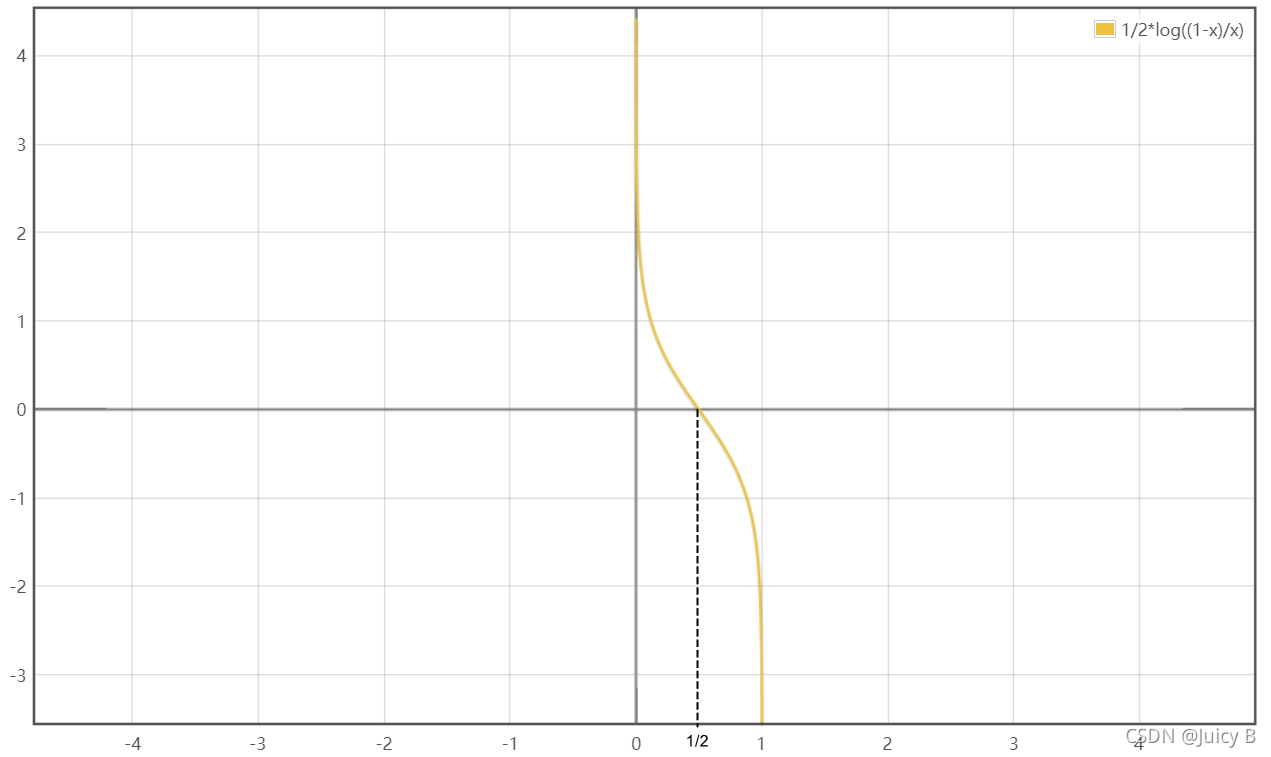   图1.3.1: 原始AdaBoost算法弱分类器权重更新函数的图像

   可以看到，只有当 ϵ t < 0.5 \epsilon_t<0.5 ϵt​<0.5时， w t w_t wt​才大于0。

   • 改进之后的计算公式为：

     w t = 1 2 l n ( 1 − ϵ t ϵ t ) + l n ( ∣ Y ∣ − 1 ) w_t=\frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})+ln(|Y|-1) wt​=21​ln(ϵt​1−ϵt​​)+ln(∣Y∣−1)

   其中 Y Y Y是数据集中所有类别的标签所组成的集合， ∣ Y ∣ |Y| ∣Y∣数据集中的总类别数。可以看到，SAMME算法在计算基学习器的权重时多了 l n ( ∣ Y ∣ − 1 ) ln(|Y|-1) ln(∣Y∣−1)这一项，所以当 ∣ Y ∣ = 2 |Y|=2 ∣Y∣=2时，SAMME算法等价于AdaBoost算法。为了能更直观地理解加入 l n ( ∣ Y ∣ − 1 ) ln(|Y|-1) ln(∣Y∣−1)的作用，我们取 ∣ Y ∣ = 3 |Y|=3 ∣Y∣=3，绘制此时 w t w_t wt​的函数曲线如下:

   

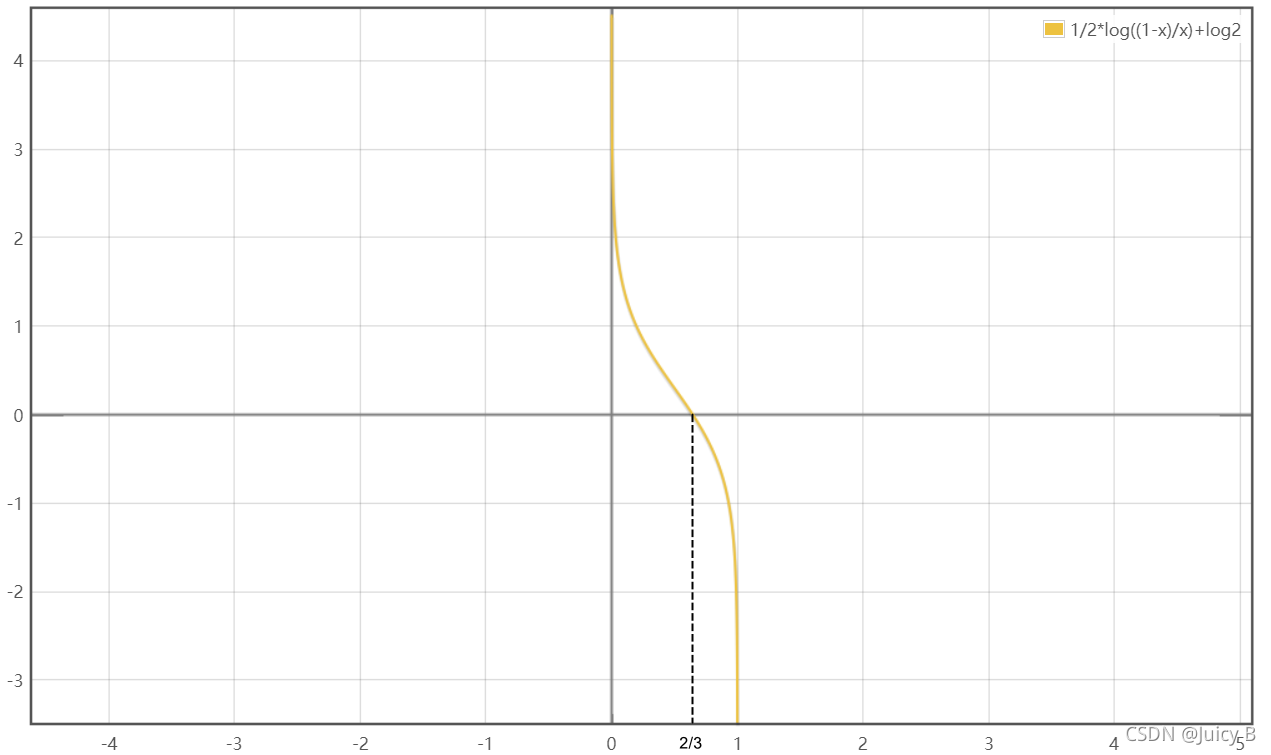   图1.3.2: 使用了SAMME算法并取|γ|=3时AdaBoost算法弱分类器权重更新函数的图像

可以看到，当 ϵ t < 2 / 3 \epsilon_t<2/3 ϵt​<2/3时，$w_t $就可以大于0。

取 ∣ Y ∣ = 4 |Y|=4 ∣Y∣=4，绘制此时 w t w_t wt​的函数曲线如下:

可以看到，当 ϵ t < 3 / 4 \epsilon_t<3/4 ϵt​<3/4时，$w_t $就可以大于0，

通过观察和比较上面三个函数曲线图，可以看到，随着总类别数 ∣ Y ∣ |Y| ∣Y∣的增加，函数曲线的零点不断右移，即使得 w t > 0 w_t>0 wt​>0的 ϵ t \epsilon_t ϵt​阈值越来越大。所以，通俗来讲， l n ( ∣ Y ∣ − 1 ) ln(|Y|-1) ln(∣Y∣−1)的作用是：随着总类别数的增加，对基学习器分类错误的宽恕度也不断增加，使得原始的AdaBoost算法可以从二分类任务泛化到多分类任务中。

1.3.2.2 SAMME.R算法

SAMME算法虽然将原始的AdaBoost从二分类扩展到了多分类，但是它的其他步骤跟AdaBoost几乎是完全一样的，包括每一个弱分类器的输出结果都是离散的标签值的形式。这使得SAMME算法的迭代速度较慢，连续性较差。针对这一缺点，SAMME.R算法被提出。

SAMME.R算法的步骤与SAMME有所不同。下面我们来具体分析。

假设有一个如下的二分类的数据集，它由 m m m 个样本组成：

D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D= \{ (\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),...,(\boldsymbol x_m,y_m)\} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)}

并假设数据集总的类别数为 C C C，则 y i ∈ { 0 , 1 , 2 , . . . , C − 1 } y_i\in\{0,1,2,...,C-1\} yi​∈{0,1,2,...,C−1}。

具体步骤如下：

1. 初始化权重。记初始状态下的数据集样本分布为 D i s t 1 ( x ) Dist_1(\boldsymbol x) Dist1​(x)，每一个样本的权重均初始化为 1 / m 1/m 1/m，则 D i s t 1 ( x ) = 1 / m Dist_1(\boldsymbol x)=1/m Dist1​(x)=1/m， D i s t 1 ( x ) Dist_1(\boldsymbol x) Dist1​(x)分布用于第一个弱分类器 h 1 h_1 h1​的训练；

2. 循环进行 T T T 轮迭代，记每一轮迭代中弱分类器的编号为 t t t，且 t ∈ { 1 , 2 , 3 , . . . , T } t \in \{1,2,3,...,T\} t∈{1,2,3,...,T}。以该步骤为循环体，循环体中的步骤进一步细分为：

   1. 在样本分布为 D i s t t ( x ) Dist_t(\boldsymbol x) Distt​(x)的基础上，在数据集 D D D上训练弱分类器 h t h_t ht​；

   2. 求出 h t h_t ht​对样本 x \boldsymbol x x的分类概率估计值（即样本 x \boldsymbol x x属于各个类别的概率），计算公式为：

h k t ( x ) = P x ～ D i s t t { c = k   ∣   x } , k ∈ { 0 , 1 , 2 , . . . , C − 1 } h^{t}_k(\boldsymbol x)=P_{\boldsymbol x ～ Dist_t}\{c=k\,|\,\boldsymbol x\},\quad k\in\{0,1,2,...,C-1\} hkt​(x)=Px～Distt​​{c=k∣x},k∈{0,1,2,...,C−1}

如 h 0 t ( x ) h^{t}_0(\boldsymbol x) h0t​(x)就表示弱分类器 h t h_t ht​预测出样本 x \boldsymbol x x属于类别0的概率;

3. 在上一步的基础上求出 s k t ( x ) s^t_k(\boldsymbol x) skt​(x)，计算公式为：
   s k t ( x ) = ( C − 1 ) ( l o g   h k t ( x ) − 1 C ∑ i = 0 C − 1 l o g   h i t ( x ) ) , k ∈ { 0 , 1 , 2 , . . . , C − 1 } s^t_k(\boldsymbol x)=(C-1)\bold (log\,h^{t}_k(\boldsymbol x)-\frac{1}{C}\sum_{i=0}^{C-1}log\,h^{t}_i(\boldsymbol x)\bold),\quad k\in\{0,1,2,...,C-1\} skt​(x)=(C−1)(loghkt​(x)−C1​i=0∑C−1​loghit​(x)),k∈{0,1,2,...,C−1}

4. 根据上面求出的权重 s k t ( x ) s^t_k(\boldsymbol x) skt​(x)对数据集样本的分布权重进行更新，对于第 i i i个样本，其权重更新的计算公式为：
   D t + 1 ( i ) = 1 Z t e x p ( − C − 1 C z i T l o g   h t ( x ) ) , i ∈ { 1 , 2 , . . . , m } D_{t+1}(i)=\frac{1}{Z_t}exp\bold({-\frac{C-1}{C}\boldsymbol z_i^Tlog\,\boldsymbol h^t(\boldsymbol x)}\bold ),\quad i\in\{1,2,...,m \} Dt+1​(i)=Zt​1​exp(−CC−1​ziT​loght(x)),i∈{1,2,...,m}
   其中 Z t Z_t Zt​为归一化因子，向量 z i = ( z i 1 , z i 2 , . . . , z i C ) \boldsymbol z_i=(z_{i1},z_{i2},...,z_{iC}) zi​=(zi1​,zi2​,...,ziC​)，且：
   z i k = { 1 , k = y i − 1 C − 1 , k ≠ y i z_{ik}=\left\{ \begin{aligned} 1, \quad k=y_i\\ -\frac{1}{C-1},\quad k \ne y_i \end{aligned} \right. zik​=⎩⎨⎧​1,k=yi​−C−11​,k​=yi​​
   向量 h t ( x ) = ( h 0 t ( x ) , h 1 t ( x ) , . . . , h C − 1 t ( x ) ) \boldsymbol h^t (\boldsymbol x)=\bold(h_0^t(\boldsymbol x),h_1^t(\boldsymbol x),...,h_{C-1}^t(\boldsymbol x)\bold ) ht(x)=(h0t​(x),h1t​(x),...,hC−1t​(x))，由 h ( t ) h(t) h(t) 对样本 x \boldsymbol x x的预测概率组成；

5. 令 t : = t + 1 t := t+1 t:=t+1，回到循环体中的步骤1。

6. 结束 T T T轮迭代，最终得到强分类器如下：
   H ( x ) = arg ⁡ max ⁡ k ∑ t = 1 T s k t ( x ) H(\boldsymbol x)=\mathop{\arg\max}_k \sum_{t=1}^T s^t_k(\boldsymbol x) H(x)=argmaxk​t=1∑T​skt​(x)
   意思就是说，每个不同的弱分类器 h t h_t ht​对每个类别 k k k都会输出一个 s k t ( x ) s^t_k(\boldsymbol x) skt​(x)值，若对于所有的弱分类器 h ( t ) h(t) h(t)，类别 k k k的 s k t ( x ) s^t_k(\boldsymbol x) skt​(x)值的和最大，则该 k k k值就是强分类器 H ( x ) H(x) H(x)的输出结果，也就是强分类器对样本预测出来的标签。

通过如上步骤，就完成了AdaBoost算法的扩展算法SAMME.R的全过程。

1.3.3 sklearn中的Adaboost分类算法

sklearn中的AdaBoostClassifier类对AdaBoost分类算法进行了实现。下面将对这个类进行详细介绍。

1.3.3.1 原型

原型如下：
class sklearn.ensemble. AdaBoostClassifier(base_estimator=None,*, n_estimators=50,learning_rate=1.0,algorithm='SAMME.R', random_state=None)

1.3.3.2 参数

上述原型中各参数的解释如下：

• base_estimator： 对象类型，默认值为None
  该参数设置为None时，使用默认基学习器DecisionTreeClassifier(max_depth=1),即默认使用深度为1的CART树。

• algorithm： 可选参数，默认为SAMME.R。scikit-learn实现了两种Adaboost分类算法：SAMME和SAMME.R。两者的主要区别在于基学习器权重的度量方法：

  • SAMME使用对数据集的分类效果作为基学习器的权重；
  • SAMME.R使用对数据集分类的预测概率大小来作为基学习器的权重。

  由于SAMME.R使用了概率度量的连续值，迭代速度一般比SAMME快，因此AdaBoostClassifier的algorithm参数默认值也设置为SAMME.R。注意：若使用的是SAMME.R算法，则base_estimator参数必须限制使用支持概率预测的分类器，SAMME算法则没有这个限制。

• n_estimators： 整型，默认值为50
  基学习器的最大迭代次数（即最大的基学习器个数）。AdaBoost的分类效果对n_estimators取值的敏感性较高：

  • n_estimator太小，基学习器数量太少，容易造成欠拟合；

  • n_estimators太大，基学习器数量太多，容易造成过拟合；

  所以，在实际使用中，n_estimators的值不宜过大，也不能太小，需要通过调参找到一个合适的取值。在实际调参的过程中，常常将n_estimators和下面要介绍到的参数learning_rate一起考虑。

• learning_rate： 浮点型，默认为1.0
  表示每个基学习器的权重缩减系数（即1.3.1小节中的 w t w_t wt​）。该参数对AdaBoost分类效果的影响也很大，所以在实际使用中，需要通过调参，在n_estimators和learning_rate这两个参数之间找到平衡。在实例2中将会对这一过程做详细的探索。

• random_state： 整型，默认为None
  为每个基学习器设置相同的随机数种子，确保多次运行所生成的随机数状态均一致，便于调参与观察。

1.3.3.3 属性

AdaBoostingClassifier类有很多属性，如下：

• base_estimator_：返回基学习器（包括种类、详细参数等信息）。
• estimators_：返回对数据集进行拟合之后的所有基学习器所组成的列表。
• classes_：返回所有类别的标签。
• n_class：返回总类别数。
• estimator_weights_：返回每个基学习器所对应权重所组成的列表。
• estimator_errors_：返回每个基学习器的分类错误率所组成的列表。
• feature_importances_：返回数据集中每个特征的权重的组成的列表。

1.3.3.4 常用方法

AdaBoostingClassifier类有很多方法，常用的方法如下：

• decision_function(X)：得到分类器对数据集 X X X中各个样本的计算结果，分为如下两种情况：

  • 若数据集只有两个类别，则返回的计算结果的尺寸为 s h a p e = ( 样 本 数 , 1 ) shape=(样本数,1) shape=(样本数,1)；
  • 若数据集有 k ( k > 2 ) k(k > 2) k(k>2)个类别，则返回的计算结果的尺寸为 s h a p e = ( 样 本 数 , k ) shape=(样本数,k) shape=(样本数,k)。

  以二分类为例，假设AdaBoost分类器abt对样本 x x x的计算结果 abt.decision_functiuon(x)=[-0.009] ，由于-0.009到0的距离比到1的距离更近，所以分类器预测 x x x属于类别0；

  假设abt对样本 x x x的计算结果 abt.decision_functiuon(x)=[0.999] ，由于0.999到1的距离比到0的距离更近，所以分类器预测 x x x属于类别1。多分类任务也同理。

• fit(X,y,[,sample_weight]：拟合数据集。

• get_params([deep])： d e e p deep deep参数指定为 T r u e True True 时，返回集成分类器的各项参数值。

• predict(X)：对样本进行预测。

• predict_proba(X)：计算出样本 X X X属于各个类别的概率。

• predict_log_proba(X)：预测结果以概率值的自然对数值返回。

  ( 这里简单介绍一下上面两种方法的区别。比如在一个二分类任务中，AdaBoost分类器abt对一个样本 x x x的预测结果为[[0.8, 0.2]]，即 abt.predict_proba(x)= [[0.8,0.2]] ，表示该分类器预测出 x x x属于类别0的概率为 0.8 0.8 0.8、属于类别1的概率为0.2​；然后再对这两个值分别取自然对数，返回的结果为[[-0.2231, -1.6094]]，即 abt.predict_log_proba(x)=[[-0.2231, -1.6094]] )

1.3.4 实例1：使用AdaBoost完成二分类任务

1.3.4.1 创建数据集

此处选择用sklearn中make_gaussian_quantiles函数创建多维的、满足正态分布的二分类数据集。该函数主要参数有：

• n_sample：生成的总样本数。
• n_features：每个样本的维数（特征数）。
• mean：各个特征的均值，默认为每个特征的平均值均设为0。
• cov：样本协方差的系数，通过调整该参数可以控制数据集分布的密集程度。
• n_classes：总类别数。

创建数据集的代码如下：

# 第一组样本
X1, y1 = make_gaussian_quantiles(mean=(2, 2), cov=1,
                                 n_samples=200, n_features=2,
                                 n_classes=2, random_state=1)
# 第二组样本
X2, y2 = make_gaussian_quantiles(mean=(3, 3), cov=2,
                                 n_samples=500, n_features=2,
                                 n_classes=2, random_state=1)

#  将两组样本混在一起，组合成一个数据集
X = np.concatenate((X1, X2))
y = np.concatenate((y1, 1 - y2))

1.3.4.2 可视化数据集

代码如下：

# 取出数据集X中第一个第一个特征，获取最大值和最小值确定第一个特征数值的范围
x1_min= X[:, 0].min() - 1
x1_max = X[:, 0].max() + 1

# 取出数据集X中第一个第二个特征，获取最大值和最小值确定第一个特征数值的范围
x2_min = X[:, 1].min() - 1
x2_max = X[:, 1].max() + 1

# 设置输出图的尺寸
plt.figure(figsize=(8,8))
# 获取标签为0的样本点的索引
index0 = np.where(y == 0)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index0, 0], X[index0, 1], c='g', s=30, edgecolor='k', label="Class 1")    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 获取标签为1的样本点的索引
index1 = np.where(y == 1)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index1, 0], X[index1, 1], c='r', s=30,edgecolor='k', label="Class 2")    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Training Set')

输出结果如下：

1.3.4.3 AdaBoost模型的调参与拟合

本例中AdaBoost的基学习器全部选用决策时中的CART树，这就引入了一个非常重要的超参数：sklearn中实现决策的DecisionTreeClassifier类中表示树的最大深度的参数max_depth，该参数会对AdaBoost的分类效果产生非常大的影响。在这个例子中，会对max_depth取不同的值，并将各自的分类结果进行可视化，对比不同max_depth下分类效果的差异。

而在AdaBoostClassifier类中则有两个非常重要的参数：表示最大迭代次数的参数n_estimator，以及表示学习率的参数 learning_rate。
接下来构建一个AdaBoost模型。该模型的基学习器全部为深度为1的CART树。由于在实际使用中n_estimators和learning_rate这两个参数对模型性能的影响较大，所以下面将在固定基学习器深度为1的基础上对这两个参数进行网格搜索调参。另外，在1.5.3.1 小节中，我们会打印出讯训练好的AdaBoost分类器的一些常用属性，并对类中的一些常用函数的使用方法做演示，旨在加深读者对AdaBoostClassifier类各个属性和方法的理解，但由于这样做太占篇幅，所以在其他小节中则不再涉及。代码如下：

max_depth=1

# 定义基学习器决策树的深度为1
abt_max_depth1 = AdaBoostClassifier( DecisionTreeClassifier(max_depth=1))

n_estimators_range = np.arange(50, 500, 50)
learning_rate_range = np.arange(0.1, 1.1, 0.1)
param_grid = dict(n_estimators = n_estimators_range, learning_rate = learning_rate_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=1)
grid1 = GridSearchCV(estimator=abt_max_depth1, param_grid=param_grid,  cv = cv, n_jobs=-1)
grid1.fit(X, y)

# 打印出网格搜搜中得到的最佳参数组合与其对应的最佳平均验证准确率
print("Best parameters :", grid1.best_params_)
print("Best score :%.4f" % (grid1.best_score_*100),"%")

# 通过best_estimator_获取最佳分类器
abt_max_depth1_best = grid1.best_estimator_
print("Best estimator abt_max_depth1_best created.")

# 打印出Abase_estimator_属性
abt_max_depth1_best_base = abt_max_depth1_best.base_estimator_
print('Base estimator of abt_max_depth1_best:\n', abt_max_depth1_best_base)

# 使用get_params方法获取分类器的各个参数
print('Parameters of abt_max_depth1_best:')
print(abt_max_depth1_best.get_params(True))

输出结果如下：

• Best parameters : {‘learning_rate’: 0.3, ‘n_estimators’: 250}

  #得到网格搜索得到的最佳参数组合；

• Best score :77.1429 %

  #得到最佳参数组合所对应分类器的平均验证准确率；

• Best estimator abt_max_depth1_best created.

  #获得最佳分类器；

• Base estimator of abt_max_depth1_best:
  DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion=‘gini’,
  max_depth=1,
  max_features=None,
  max_leaf_nodes=None,
  min_impurity_decrease=0.0,
  min_impurity_split=None,
  min_samples_leaf=1, min_samples_split=2,
  min_weight_fraction_leaf=0.0,
  presort=‘deprecated’,
  random_state=None, splitter=‘best’)
  #获得基学习器种类和参数的详细信息；

• Parameters of abt_max_depth1_best:
  {‘algorithm’: ‘SAMME.R’,
  ‘base_estimator__ccp_alpha’: 0.0,
  ‘base_estimator__class_weight’: None,
  ‘base_estimator__criterion’: ‘gini’,
  ‘base_estimator__max_depth’: 1,
  ‘base_estimator__max_features’: None,
  …,
  ‘learning_rate’: 0.3,
  ‘n_estimators’: 250,
  ‘random_state’: None}
  #获得集成学习器的各项详细信息；

输出结果由三部分组成:

1. 网格搜索得到的最佳参数组合；
2. 最佳参数组合所对应分类器的平均验证准确率；
3. 基学习器的种类及其详细参数。

max_depth=2

接下来固定基学习器树的深度为2，同样用上面的方法进行调参，得出结果。代码如下：

# 定义基学习器决策树的深度为2
abt_max_depth2 = AdaBoostClassifier( DecisionTreeClassifier(max_depth=2))

n_estimators_range = np.arange(50, 500, 50)
learning_rate_range = np.arange(0.1, 1.1, 0.1)
param_grid = dict(n_estimators = n_estimators_range, learning_rate = learning_rate_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=1)
grid2 = GridSearchCV(estimator=abt_max_depth2, param_grid=param_grid,  cv=cv, n_jobs=-1)
grid2.fit(X, y)

# 打印出网格搜搜中得到的最佳参数组合与其对应的最佳平均验证准确率
print("Best parameters:", grid2.best_params_)
print("Best score: %.4f" % (grid2.best_score_*100),"%")

# 获取最佳分类器
abt_max_depth2_best = grid2.best_estimator_
print("Best estimator abt_max_depth2_best created.")

输出结果如下：

Best parameters: {‘learning_rate’: 0.2, ‘n_estimators’: 50}
Best score: 77.9048%

Best estimator abt_max_depth2_best created.

max_depth=3

现在，固定基学习器的深度为3，同样用上面的方法进行调参，依葫芦画瓢，得出结果。

输出结果如下：

Best parameters: {‘learning_rate’: 0.8, ‘n_estimators’: 200}
Best score: 79.6190 %

Best estimator abt_max_depth3_best created.

1.3.4.1 绘制决策边界

为了能绘制AdaBoost分类的决策边界，需要构造大量的网格点，并将网格点送入模型中进行预测。代码如下：

plt.figure(figsize=(15,5))

# 左图，max_depth=1
plt.subplot(131)
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.05),
                     np.arange(x2_min, x2_max, 0.05))

Z = abt_max_depth1_best.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z,  cmap=plt.cm.Pastel1_r)
plt.axis("tight")

index0 = np.where(y == 0)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index0, 0], X[index0, 1], c='g', s=20, edgecolor='k', label="Class 1" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 获取标签为1的样本点的索引
index1 = np.where(y == 1)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index1, 0], X[index1, 1], c='r', s=20, edgecolor='k', label="Class 2" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Predict result with max_depth=1')


# 中图, max_depth=2
plt.subplot(132)
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.05),
                     np.arange(x2_min, x2_max, 0.05))

Z = abt_max_depth2_best.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z,  cmap=plt.cm.Pastel1_r)
plt.axis("tight")

index0 = np.where(y == 0)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index0, 0], X[index0, 1], c='g', s=20, edgecolor='k', label="Class 1" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 获取标签为1的样本点的索引
index1 = np.where(y == 1)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index1, 0], X[index1, 1], c='r', s=20,edgecolor='k', label="Class 2" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Predict result with max_depth=2')


# 右图, max_depth=3
plt.subplot(133)
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.05),
                     np.arange(x2_min, x2_max, 0.05))

Z = abt_max_depth3_best.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z,  cmap=plt.cm.Pastel1_r)
plt.axis("tight")

index0 = np.where(y == 0)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index0, 0], X[index0, 1], c='g', s=20, edgecolor='k', label="Class 1" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 获取标签为1的样本点的索引
index1 = np.where(y == 1)    
# X[index, 0]表示数据集中的所有样本的第一个特征的值
# X[index, 1]表示数据集中的所有样本的第二个特征的值
# 以第一个特征为横轴，第二个特征为纵轴，就可以在二维空间中画出数据集
plt.scatter(X[index1, 0], X[index1, 1], c='r', s=20, edgecolor='k', label="Class 2" )    
    
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.legend(loc='upper right')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Predict result with max_depth=3')

输出结果如下：

通过上图可以很清楚地看到，随着基学习器深度的增加，验证准确率也越来越高。但是随着深度的增加，拟合的时间也会增加，AdaBoost的分类决策边界也越来越复杂，增大了过拟合的风险。因此读者在实际使用中应当先设置合适的基学习器深度，然后再在此基础上进行调参优化。

1.3.5 实例2：使用AdaBoost完成多分类任务

上一个例子中我们介绍到了如何使用AdaBoost完成二分类任务。在这个例子中，我们将深入探索如何使用AdaBoost的改进算法SAMME和SAMME.R完成多分类任务，比较这两个算法的性能差异，并对模型进行调参优化。

1.3.5.1 创建数据集

这里选择使用make_gaussian_quantiles函数创建一个满足高斯分布、样本数为10000、特征数为10、类别数为3的数据集。代码如下：

# 创建符合高斯分布的数据集
X,  y= make_gaussian_quantiles(n_samples = 10000, n_features=10, n_classes=3, random_state=111)
# 分割出训练集和测试集，训练集：测试集=7：3
X_train, X_test = X[:7000], X[7000:]
y_train, y_test = y[:7000], y[7000:]

1.3.5.2 模型的创建与拟合

两种AdaBoost分类器均使用深度为2的CART树作为基学习器。代码如下：

# 创建使用SAMME算法的AdaBoost模型
abt_samme = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=2),
    n_estimators=500,     
    learning_rate=1.0,              
    algorithm="SAMME")

# 创建使用SAMME.R算法的AdaBoost模型
abt_samme_r = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=2),
    n_estimators=500,
    learning_rate=1.0,
    algorithm='SAMME.R')

# 读取两个算法模型的learning_rate参数值，便于后续观察learning_rate对算法性能的影响
abt_samme_learning_rate = abt_samme.get_params(True)['learning_rate']
abt_samme_r_learning_rate = abt_samme_r.get_params(True)['learning_rate']

# 使用上述两个模型对数据进行拟合，并获取拟合的时间
t0_samme = time()
abt_samme.fit(X_train, y_train)
t1_samme = time()
samme_time = t1_samme - t0_samme
print("SAMME fit time with learning_rate=%.1f  is %.4fs" % (abt_samme_learning_rate, samme_time))

t0_samme_r = time()
abt_samme_r.fit(X_train, y_train)
t1_samme_r = time()
samme_r_time = t1_samme_r - t0_samme_r
print("SAMME.R fit time with learning_rate=%.1f is %.4fs" %(abt_samme_r_learning_rate, samme_r_time)) 

输出结果如下：

SAMME fit time with learning_rate=1.0 is 15.8782s
SAMME.R fit time with learning_rate=1.0 is 16.2080s

这个结果用于后续比较不同学习率对模型拟合时间的影响，先暂时保留。

1.3.5.3 获取模型的错误率和准确率

在下面的代码中，我们需要理解**“阶梯训练准确率”的含义。它和“迭代测试准确率”**的含义是不同的。这里通过一个简单的例子来对比这两个概念。

比如说，通过在训练集X_test上进行3轮迭代，生成了三个基学习器： h 1 h_1 h1​, h 2 h_2 h2​ 和 h 3 h_3 h3​。如果把它们看成彼此相互独立的个体，对测试集X_test进行预测，则可以分别得到它们三者的测试准确率，这叫做“迭代测试准确率。但如果我们把它们串联起来，那么，由 h 1 h_1 h1​ 和 h 2 h_2 h2​就可以组成一个集成学习器，由 h 1 h_1 h1​, h 2 h_2 h2​ 和 h 3 h_3 h3​又可以组成另一个集成学习器，将这两个集成学习器用于X_test的预测所得到的准确率就称为“阶梯测试准确率”。在sklearn中，使用AdaBoostClassifier.staged_predict(X_test)方法就可以获得迭代过程中的多个“阶梯测试准确率”。
对于**“阶梯训练准确率”和“迭代训练准确率”**也同理。 h 1 h_1 h1​, h 2 h_2 h2​ 和 h 3 h_3 h3​三者各自的训练准确率叫做“迭代训练准确率”，把它们串联起来组成的两个集成学习器的训练准确率称为“阶梯训练准确率”。在sklearn中，使用AdaBoostClassifier.staged_score(X_train, y_train)方法就可以获得迭代过程中的多个“阶梯训练准确率”。

这部分的代码如下：

# 获取和记录SAMME.R和SAMME两种模型的阶梯测试错误率
samme_r_test_predict_scores = abt_samme_r.staged_predict(X_test)
samme_test_predict_scores = abt_samme.staged_predict(X_test)
samme_test_errors = []
samme_r_test_errors = []

# 记录两种模型迭代训练错误率
samme_train_errors = abt_samme.estimator_errors_
samme_r_train_errors = abt_samme_r.estimator_errors_

# 记录两种模型的阶梯测试准确率
samme_test_accuracies = []
samme_r_test_accuracies = []

# 获取和记录两种模型的阶梯训练准确率
samme_r_train_scores = abt_samme_r.staged_score(X_train, y_train)
samme_train_scores = abt_samme.staged_score(X_train, y_train)
samme_train_staged_accuracies = []
samme_r_train_staged_accuracies = []

# 记录两种模型迭代训练准确率
samme_train_accuracies = np.ones(500) -abt_samme.estimator_errors_
samme_r_train_accuracies  = np.ones(500) - abt_samme_r.estimator_errors_
for samme_test_predict_score, samme_r_test_predict_score in zip(    
	samme_test_predict_scores, samme_r_test_predict_scores):    
	# SAMME模型的阶梯测试错误率    
	samme_test_errors.append(1-accuracy_score(samme_test_predict_score, y_test))    
	# SAMME.R模型的阶梯测试错误率    
	samme_r_test_errors.append(1-accuracy_score(samme_r_test_predict_score, y_test))     
	# SAMME模型的阶梯测试准确率    
	samme_test_accuracies.append(accuracy_score(samme_test_predict_score, y_test))    
	# SAMME.R模型的阶梯测试准确率    
	samme_r_test_accuracies.append(accuracy_score(samme_r_test_predict_score, y_test))   
	for samme_r_train_score, samme_train_score in zip(
	samme_r_train_scores,  samme_train_scores):    
	samme_r_train_staged_accuracies.append(samme_r_train_score)    
	samme_train_staged_accuracies.append(samme_train_score)

1.3.5.4 绘制错误率曲线

在上面的代码中我们已经记录下了两种模型的阶梯训练准确率和阶梯测试准确率。接下来我们就对它们进行可视化。

代码如下：

plt.figure(figsize=(15, 5))# 左图：画出两种模型的阶梯训练准确率曲线plt.subplot(121)plt.plot(range(1, 501), samme_train_errors, "b", label='SAMME', alpha=0.8)plt.plot(range(1, 501), samme_r_train_errors, "r", label='SAMME.R', alpha=0.8)plt.legend()plt.ylabel('Train Error')plt.xlabel('Number of Estimators')plt.xlim((-10, 510))plt.ylim((0.1, 0.7))plt.title("Train Error of Each Estimator")# 右图：画出两种模型的阶梯测试准确率曲线plt.subplot(122)# 500为迭代次数.由于range函数定义的是左闭右开区间，所以为了能取得500个数，我们要将区间右界定义为501plt.plot(range(1, 501), samme_test_errors, c='b', label='SAMME', alpha=0.6)plt.plot(range(1, 501), samme_r_test_errors, c='r', linestyle='dashed', label='SAMME.R', alpha=0.6)plt.legend()plt.ylim(0.1, 0.7)plt.ylabel('Test Error')plt.xlabel('Number of Estimators')plt.title("Test Error of Each Estimator")plt.show()

输出结果如下：

通过观察上面两张曲线图，可以对两种算法的训练和测试准确率做如下对比：

• 左图：在训练集上，随着迭代次数的增加，SAMME.R整体的迭代训练错误率比SAMME算法的要低；
• 右图：在测试集上，随着迭代次数的增加，SAMME.R算法在测试集上阶梯测试错误率的收敛速度比SAMME算法快很多，SAMME.R大概在进行到第50时就开始收敛，而SAMME大概在第100轮之后才有收敛的趋势，并且随着迭代的进行，SAMME.R算法的阶梯测试错误率比SAMME的要低很多。

通过这个例子，可以暂时得出一个结论：SAMME.R算法的性能比SAMME更好。当然现在还不能下定论，需要进一步探索。

1.3.5.5 绘制准确率曲线

接下来画出两者的阶梯训练准确率和阶梯测试准确率的曲线，从另一个角度观察对比两者的性能。代码如下：

plt.figure(figsize=(15, 5))

# 左图：画出SAMME算法模型的阶梯训练准确率和阶梯测试准确率曲线
plt.subplot(121)
plt.plot(range(1, 501), samme_train_staged_accuracies, "b", label='Train Staged Accuracy', alpha=0.6)
plt.plot(range(1, 501), samme_test_accuracies, "r", label='Test Staged Accuracy', alpha=0.6)
plt.plot(range(1, 501), samme_train_accuracies, "g", label='Train Accuracy', alpha=0.6)
plt.legend()
plt.ylabel('Accuracy')
plt.xlabel('Number of Estimators')
plt.xlim((-10, 510))
plt.ylim((0.3, 0.9))
plt.title("Accuracy Curve of SAMME")

# 右图：画出SAMME.R算法模型的阶梯训练准确率和阶梯测试准确率曲线plt.subplot(122)# 500为迭代次数（基学习器的数量）
plt.plot(range(1, 501), samme_r_train_staged_accuracies, c='b', label='Train  Staged Accuracy', alpha=0.6)
plt.plot(range(1, 501), samme_r_test_accuracies, c='r', linestyle='dashed', label='Test Staged Accuracy', alpha=0.6)
plt.plot(range(1, 501), samme_r_train_accuracies, "g", label='Train Accuracy', alpha=0.6)plt.legend()
plt.ylim(0.3, 0.9)
plt.ylabel('Accuracy')
plt.xlabel('Number of Estimators')
plt.title("Accuracy Curve of SAMME.R")
plt.show()

输出结果如下：

我们将这两个算法分开，在同一张图中对比同一个模型阶梯训练准确率、阶梯测试准确率和迭代训练准确率的差异。可以看到，不管是SAMME算法还是SAMME.R算法，随着迭代的进行，阶梯训练准确率和阶梯测试准确率都比迭代训练准确率都比要低很多，这是因为AdaBoost算法通过将多个基学习器串行地组合在一起对训练集进行训练迭代，后一个基学习器不断纠正前一个基学习器的错误，从而在总体上实现了在未知测试集上的更好表现。这也是AdaBoost算法最神奇的地方。

然而，上面这个例子是在学习率取值为1.0的情况下得到的，而学习率定义了样本权重的更新幅度。学习率越大，后一个基学习器对前一个基学习器分错的样本的“关注度”则越大；学习率越小，后一个基学习器对前一个基学习器分错的样本的“关注度”则越小。这就产生了一个疑问：这个”关注度“到底对AdaBoost算法性能的影响有多大呢？带着这个问题，下面我们就来对比下不同learning_rate取值下算法表现的差异。

1.3.5.6 探究学习率的取值对算法性能的影响

我们将从训练时间、错误率和正确率这三个方面综合评估不同学习率对SAMME和SAMME.R这两种算法性能的影响。

1 拟合时间对比

SAMME fit time with learning_rate=0.5 is 15.5212s
SAMME.R fit time with learning_rate=0.5 is 16.0056s

SAMME fit time with learning_rate=1.0 is 15.8782s
SAMME.R fit time with learning_rate=1.0 is 16.2080s

SAMME fit time with learning_rate=2.0 is 15.5729s
SAMME.R fit time with learning_rate=2.0 is 16.2028s

我们可以看到，学习率的调整对算法拟合时间的长短并没有什么影响。

2 错误率对比

接下来将绘制不同学习率下两种算法模型的阶梯测试准确率曲线和迭代训练准确率曲线，为下一步的调参和优化做指导。

learning_rate = 0.5的情况

learning_rate = 1.0的情况

learning_rate = 2.0的情况

通过观察上图，可以得知：

当learning_rate=0.5时，随着迭代次数的增加：

• 迭代训练错误率：SAMME.R的训练错误率总体上小于SAMME，但两者总体差距较小，且两者的变化曲线均较平缓。
• 阶梯测试错误率：
  • 收敛速度：SAMME.R的收敛速度比SAMME的快得多；
  • 第500轮的阶梯测试错误率：SAMME.R大约为0.22，SAMME大约为0.40。

当learning_rate=1.0时，随着迭代次数的增加：

• 迭代训练错误率：SAMME.R的训练错误率总体上仍小于SAMME，两者总体差距相比learning_rate=0.5时有所扩大，此时两者的变化曲线也都比较平缓。
• 阶梯测试错误率：
  • 收敛速度：SAMME.R的收敛速度仍然比SAMME的快得多，并且对于两种算法，learning_rate=1.0时的收敛速度均比learning_rate=0.5时更快；
  • 第500轮的阶梯测试错误率：SAMME.R大约为0.20，SAMME大约为0.32，对于两种算法，learning_rate=1.0时的第500轮的阶梯测试错误率相比learning_rate=0.5时均有所降低。

当learning_rate=2.0时，随着迭代次数的增加：

• 迭代训练错误率：
  • SAMME.R的迭代训练错误率总体上相比learning_rate=0.5和1.0时有较大幅度的下降，但是震荡的幅度很大；
  • SAMME的迭代训练错误率总体上相比learning_rate=0.5和1.0时亦有所下降， 而曲线震荡的幅度也有所增大，但没有SAMME.R那么夸张。
• 阶梯测试错误率：
  • 收敛速度：SAMME.R的收敛速度已经反过来慢于SAMME，并且对比learning_rate=0.5和1.0时的曲线，learning_rate=2.0时500轮迭代已经不足以让SAMMR.R的阶梯测试错误率收敛到一个较低、较平缓的水平；
  • 第500轮的阶梯测试错误率：SAMME.R大约为0.30，SAMME大约为0.25，在500轮迭代内，SAMME.R在测试集上错误率的表现已经不如SAMME了。

根据上面的分析可以得知，SAMME和SAMMME.R算法孰好孰坏并不能够一概而论，在学习率取值不恰当的情况下，SAMMME.R算法的表现甚至输给了SAMME算法。

3 准确率对比

下面将从准确率的角度评估两个模型的性能。

learning_rate = 0.5的情况

learning_rate = 1.0的情况

learning_rate = 2.0的情况

我们重点关注图中的红色曲线，即不同学习率下SAMME算法和SAMME.R算法的阶梯测试准确率。观察左边三张图，可以发现，当学习率从0.5→1.0→2.0时，SAMME算法第500轮迭代的阶梯测试准确率的变化趋势为：接近0.6→高于0.6低于0.7→高于0.7；观察右边三张图，可以发现，当学习率从0.5→1.0→2.0时，SAMME.R算法第500轮迭代的阶梯测试准确率的变化趋势为：约0.75→约为0.8→约0.7，因此可以推测：使得SAMME.R算法的阶梯测试准确率最高的学习率取值应该在1.0附近。还可以发现，在学习率的取值较为合适的前提下，SAMME.R算法的表现比SAMME要好很多。综合以上分析，下面将从三个角度尝试对该问题进行优化，看能否将这个分类问题优化到一个更高的测试准确率水平：

1. 选用SAMME.R算法代替SAMME算法进行进一步优化；
2. 在选择SAMME.R算法的基础上，取一个均值为1.0的学习率区间进行调参；
3. 尝试增加迭代次数。

1.3.5.7 问题的进一步优化

1 模型定义与网格搜索

这里的基学习器仍然选用深度为2的CART树，与前面保持一致，便于对比。

# 定义模型
abt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=2))
# 定义网格搜索中学习率的范围
learning_rate_range = np.arange(0.6, 1.5, 0.1)
#  定义网格搜索中迭代次数的范围
n_estimators_range = np.arange(600, 1100, 100)

# 定义网格搜索
param_grid = dict(n_estimators = n_estimators_range, learning_rate = learning_rate_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=1)grid1 = GridSearchCV(estimator=abt, param_grid=param_grid,  cv = cv, n_jobs=-1)
t0 = time()
grid1.fit(X_train, y_train)
t1 = time()total_time = t1 - t0

# 打印出总的搜索时间
print("Total time: %.4fs" % total_time)
# 打印出搜索出的最佳参数组合
print("Best parameters: ", grid1.best_params_)
# 打印出最佳分类器的平均验证准确率
print("Best score: %.6f" % grid1.best_score_)

输出结果如下：

Total time: 880.3537s

Best parameters: {‘learning_rate’: 1.4, ‘n_estimators’: 1000}
Best score: 0.817619

我们得到：在学习率取值为1.4、迭代次数为1000时，平均验证准确率最高。这与我们前面的推测相吻合。然而，将迭代次数的区间设置为[600, 700, 800, 900, 1000]非常耗时，因此后续需要考虑减小迭代次数。

2 最佳分类器的拟合

代码如下：

# 获取网格搜索中得到的最佳分类器
abt_best = grid1.best_estimator_
# 使用该最佳分类器对训练集进行拟合
abt_best.fit(X_train, y_train)

# 记录阶梯训练准确率
abt_best_staged_train_accuracies = []
# 记录迭代训练准确率
abt_best_train_accuracies = np.ones(1000) - abt_best.estimator_errors_
# 记录阶梯测试准确率
abt_best_test_accuracies = []

for abt_best_staged_train_accuracy, abt_best_test_accuracy in zip(
	abt_best.staged_score(X_train, y_train), abt_best.staged_predict(X_test)):    
	abt_best_staged_train_accuracies.append(abt_best_staged_train_accuracy)    
	abt_best_test_accuracies.append(accuracy_score(abt_best_test_accuracy, y_test)) 

3 绘制最佳分类器的准确率曲线

最后画出 algorithm=‘SAMME.R’, earning_rate=1.4, n_estimators=1000 这一最佳分类器的准确率曲线如下：

# 画图
plt.figure(figsize=(7, 5))
# 阶梯训练准确率用蓝色点划线表示
plt.plot(range(1, 1001), abt_best_staged_train_accuracies, c='b', linestyle='dotted', label='Train Staged Accuracy', alpha=0.8)
#  阶梯测试准确率曲线用红色虚线表示
plt.plot(range(1, 1001), abt_best_test_accuracies, c='r', linestyle='dashed', label='Test Staged Accuracy', alpha=0.8)
#  迭代训练准确率用绿色实线表示
plt.plot(range(1, 1001), abt_best_train_accuracies, c='g', label='Train Accuracy', alpha=0.8)

plt.legend()
plt.ylim(0.30, 0.95)
plt.ylabel('Accuracy')
plt.xlabel('Number of Estimators')
plt.title("Accuracy Curve of abt_best")
plt.show()

与图1.3.7做对比，可以看出，当 learning_rate 从1.0调整到1.4、n_estimators从500调整到1000时，使用SAMME.R算法的最终阶梯测试准确率有了明显提高。下面我们来看看具体提高了多少。

# 获取 algorithm='SAMME.R', learning_rate=1.0, n_estimators=500时的最终测试准确率
print("algorithm='SAMME.R', learning_rate=1.0, n_estimators=500 final test accuracy: %.3f" % samme_r_test_accuracies[499])
print("algorithm='SAMME.R', learning_rate=1.4, n_estimators=1000 final test accuracy: %.3f" % abt_best_test_accuracies[999])

输出结果如下：

algorithm=‘SAMME.R’, learning_rate=1.0, n_estimators=500 final test accuracy: 0.808
algorithm=‘SAMME.R’, learning_rate=1.4, n_estimators=1000 final test accuracy: 0.845

通过上面的分析与调参，成功将测试准确率提升了大约4个百分点，这看起来是非常大的提升。然而还是有瑕疵。观察曲线可以发现，当迭代次数超过200时，阶梯测试准确率曲线上升的速度已经很慢，而阶梯训练准确率曲线的上升速度则快得多，随着迭代次数的增加，两条曲线分得越来越远。这使得模型过拟合的风险不断上升，同时又浪费了大量的计算资源，消耗了大量的时间。因此，将迭代次数设置为1000并不是一个很好的选择，所以下面将采用“Early stopping"机制，使迭代次数减少的同时又不造成大的测试准确率损失。通过观察曲线，较合理的迭代次数区间应该在[200, 400]。所以选择在这个区间做Early stopping。实现代码如下：

# 取出abt_best模型阶梯测试准确率数组中的第200到第400个数
abt_best_test_accuracies_small = abt_best_test_accuracies[200:400]
# 将abt_best_test_accuracies_small转化为np.array类型，才能调用下面的argsort()方法
abt_best_test_accuracies_small = np.array(abt_best_test_accuracies_small )
# 将[200,400]区间内的索引按准确率按从大到小的顺序进行排序
abt_best_test_accuracies_indexes =  abt_best_test_accuracies_small.argsort()[::-1]
abt_best_test_accuracies_indexes  = abt_best_test_accuracies_indexes+200
# 打印出[200, 400]区间内准确率最高的前20个数值所对应的索引
print(abt_best_test_accuracies_indexes[:20])

输出结果：

[375 248 391 376 340 313 330 341 253 246 378 379 232 329 226 328 392 247
390 251]

排名第一和第二的迭代次数分别仅为375次和248次。我们来看一下对应位置上的准确率：

abt_best_test_accuracies[375]

输出结果为：

0.8433333333333334

abt_best_test_accuracies[248]

输出结果为：

0.842

可以看到，将1000的迭代次数降低到375，迭代次数减少了675，测试错误率则从0.845减少到了约0.843，仅降低了0.002；而将迭代次数降到248，迭代次数减少了752，测试准确率则从0.845降低到了0.842，仅降低了0.003。所以，综合考虑，选用375或248的迭代次数比选择1000更加明智。当然在实际场景中，有时0.003或0.002的精度下降幅度也是不可接受的，还需要各位读者”对症下药“。

1.4 AdaBoost回归算法

1.4.1 概要

AdaBoost算法不仅可以用于分类任务，还可以用于回归任务。由于回归预测得到的结果是连续数值，如股票价格，由于股票价格走势曲线是连续的，所以股票价格在实数范围内有非常多可能的数值，不像分类任务中的类别标签一样仅仅只有若干个固定的整数值。由于在分类任务中，样本权重的更新幅度与样本的类别息息相关，而在回归任务中用“目标数值”代替了分类标签，因此，AdaBoost回归算法更新样本权重的方式与AdaBoost分类算法有较大差异。下面将对AdaBoost回归算法做详细介绍。

1.4.2 算法步骤

假设有一个如下数据集，它由 m m m个样本组成：
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D= \{ (\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),...,(\boldsymbol x_m,y_m)\} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)}
其中， x i ∈ R d \boldsymbol x_i\in\mathbb{R}^d xi​∈Rd（每一个样本数据有 d d d 个特征）， y i y_i yi​为样本 x i \boldsymbol x_i xi​的目标数值 。AdaBoost回归算法的具体步骤如下：

1. 初始化权重。记初始状态下的数据集样本分布为 D i s t 1 Dist_1 Dist1​，对每一个样本 x i \boldsymbol x_i xi​的权重均初始化为 1 / m 1/m 1/m，则 D i s t 1 ( x i ) = 1 / m Dist_1(\boldsymbol x_i)=1/m Dist1​(xi​)=1/m。 D i s t 1 Dist_1 Dist1​分布用于第一个弱分类器 h 1 h_1 h1​的训练， D i s t t Dist_t Distt​分布用于第一个弱分类器 h t h_t ht​的训练，其他同理；

2. 循环进行 T T T 轮迭代，记每一轮迭代中弱分类器的编号为 t t t，且 t ∈ { 1 , 2 , 3 , . . . , T } t \in \{1,2,3,...,T\} t∈{1,2,3,...,T}。以该步骤作为循环体，循环体中的步骤进一步细分为：

   1. 在样本分布为 D i s t t ( x ) Dist_t(\boldsymbol x) Distt​(x)的基础上，在数据集 D D D上训练弱分类器 h t h_t ht​；

   2. 计算分类器 h t h_t ht​在训练集 D D D上的最大误差 E t E_t Et​，计算公式为：
      E t = m a x ∣ y i − h t ( x i ) ∣ , i = 1 , 2 , . . . , m E_t=max|y_i-h_t(\boldsymbol x_i)|, \quad i=1,2,...,m Et​=max∣yi​−ht​(xi​)∣,i=1,2,...,m
      其中， h t ( x i ) h_t(\boldsymbol x_i ) ht​(xi​)表示弱分类器 h t h_t ht​对样本 x i \boldsymbol x_i xi​的预测结果， y i y_i yi​表示样本 x i \boldsymbol x_i xi​的目标数值；

   3. 根据上面求得的 h t h_t ht​的最大误差 E t E_t Et​，计算 h t h_t ht​对每个样本的相对误差，其计算方法有很多种，这里以平方误差为例：
      e t i = ( y i − h t ( x i ) ) 2 E t 2 , i = 1 , 2 , . . . , m e_{ti}=\frac {\bold(y_i-h_t(\boldsymbol x_i)\bold)^2}{E_t^2}, \quad i=1,2,...,m eti​=Et2​(yi​−ht​(xi​))2​,i=1,2,...,m

   4. 根据上一步求得的样本相对误差 e t i e_{ti} eti​，计算出当前弱分类器 h t h_t ht​的误差率：
      e t = ∑ i = 1 m D i s t t ( x i ) e t i e_t= \sum_{i=1}^mDist_t(\boldsymbol x_i)e_{ti} et​=i=1∑m​Distt​(xi​)eti​
      即数据集中所有样本的权重与误差之乘积的和；

   5. 更新当前弱分类器 h t h_t ht​的权重，计算公式为：
      w t = e t 1 − e t w_t = \frac{e_t}{1-e_t} wt​=1−et​et​​

      6. 更新数据集样本的权重分布，对于样本 x i \boldsymbol x_i xi​，更新权重的计算公式为：
         D i s t t + 1 ( x i ) = D i s t t ( x i ) Z t w t 1 − e t i Dist_{t+1}(\boldsymbol x_i)=\frac{Dist_t(\boldsymbol x_i)}{Z_t}w_t^{1-e_{ti}} Distt+1​(xi​)=Zt​Distt​(xi​)​wt1−eti​​
         其中， Z t Z_t Zt​为归一化因子，其计算公式为：
         Z t = ∑ i = 1 m D i s t t ( x i ) w t 1 − e t i Z_t = \sum_{i=1}^mDist_t(\boldsymbol x_i)w_t^{1-e_{ti}} Zt​=i=1∑m​Distt​(xi​)wt1−eti​​

   6. 令 t : = t + 1 t := t+1 t:=t+1，回到循环体中的步骤1。

3. 结束 T T T轮迭代，最终得到强回归器如下：
   H ( x ) = ∑ i = 1 m l n ( 1 w t ) f ( x ) = [ ∑ i = 1 m l n ( 1 w t ) ] f ( x ) H(\boldsymbol x)=\sum_{i=1}^mln(\frac{1}{w_t})f(\boldsymbol x)=\bold [\sum_{i=1}^mln(\frac{1}{w_t})\bold ]f(\boldsymbol x) H(x)=i=1∑m​ln(wt​1​)f(x)=[i=1∑m​ln(wt​1​)]f(x)
   其中， f ( x ) f(\boldsymbol x) f(x)是所有 w t h t ( x ) w_th_t(\boldsymbol x) wt​ht​(x) ( t = 1 , 2 , . . . , T ) (t=1,2,...,T) (t=1,2,...,T)的中位数，即所有弱学习器的加权输出结果的中位数。

   这样就完成了AdaBoost算法的全过程。

1.4.3 sklearn中的AdaBoost回归

sklearn中的AdaBoostRegressor类对AdaBoost回归算法进行了实现，供用户使用。下面将对这个类进行详细介绍。

1.4.3.1 原型

原型如下：
class sklearn.ensemble.AdaBoostRegressor(base_estimator=None, *, n_estimators=50, learning_rate=1.0, loss='linear', random_state=None)[source]

1.4.3.2 参数

上述原型中各参数的解释如下，其中一些参数的含义与AdaBoostClassifier类的一致，因此对这些参数就不做详细介绍，读者可以翻到1.4小节查阅。

• base_estimator： 对象类型，默认值为None
  该参数不指定时，使用DecisionTreeRegressor(max_depth=3)作为基学习器，即默认使用深度为3的回归决策树。

• n_estimators： 整型，默认值为50
  基学习器的最大迭代次数（即最大的基学习器个数）。

• learning_rate： 浮点型，默认为1.0
  表示每个基学习器的权重缩减系数。

• loss：可选项为 {‘linear’, ‘square’, ‘exponential’}，默认为‘linear’

  定义误差函数（即1.7.2小节中的 e t i e_{ti} eti​），各个选项的含义如下：

  • ‘linear’：线性损失函数
  • ‘square’：平方损失函数
  • ‘exponential’：指数损失函数

• random_state： 整型，默认为None
  为每个基学习器设置相同的随机数种子，确保多次运行所生成的随机数状态均一致，便于调参与观察。

1.4.3.3 属性

AdaBoostingRegressor类的全部属性只有5个，比AdaBoostingClassifier类少。如下：

• base_estimator_：返回基学习器（包括种类、详细参数等信息）。
• estimators_：返回对数据集进行拟合之后的所有基学习器所组成的列表。
• estimator_weights_：返回每个基学习器所对应权重所组成的列表。
• estimator_errors_：返回每个基学习器的回归损失所组成的列表。
• feature_importances_：返回数据集中每个特征的权重的组成的列表。

1.4.3.4 常用方法

AdaBoostingRegressor类的常用方法如下：

• fit(X,y,[,sample_weight]：拟合数据集。
• get_params([deep])： d e e p deep deep参数指定为 T r u e True True 时，返回集成回归器的各项参数值。
• predict(X)：对样本数据集 X X X进行回归预测，返回预测出的数值。
• staged_predict(X)：获取对数据集 X X X的阶梯测试准确率（1.6.3小节对这个概念已有介绍）。
• staged_score(X)：获取对数据集 X X X的阶梯训练准确率（1.6.3小节对这个概念已有介绍）。
• set_params(**params)：以字典的形式传入参数**params，设置集成学习器的各项参数。

1.4.4 实例3：使用AdaBoostRegressor完成回归任务

接下来将演示如何使用AdaBoostRegressor类完成一个简单的回归任务，并对不同参数取值下的拟合效果进行可视化，使得读者可以直观感受到各个参数的作用。

1.4.4.1 数据集的创建与可视化

这里选择叠加正弦曲线，并加上高斯噪声的方式来创建数据集。这样的数据集非常适合用来测试、对比和可视化回归算法的性能。代码如下：

# 创建随机数种子
rng = np.random.RandomState(111)
# 训练集X为300个0到10之间的随机数
X = np.linspace(0, 10, 300)[:, np.newaxis]
# 定义训练集X的目标变量
y = np.sin(1*X).ravel() + np.sin(2*X).ravel() + np.sin(3* X).ravel()+np.cos(3*X).ravel() +rng.normal(0, 0.3, X.shape[0])

plt.figure(figsize=(10, 6))
plt.scatter(X, y, c='k', label='data', s=10, zorder=1, edgecolors=(0, 0, 0))
plt.xlabel("X")
plt.ylabel("y", rotation=0)
plt.show()

输出结果如下：

1.4.4.2 不同参数的AdaBoost回归器拟合效果对比

接下来将从两个方面对比不同参数取值下AdaBoost回归器的回归效果。

1 固定基学习器最大深度

固定基学习器（回归决策树）的最大深度为4，调节迭代次数分别为1、10和100，对比拟合效果。

代码如下：

# 定义不同迭代次数的AdaBoost回归器模型
adbr_1 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=1, random_state=123)
adbr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=10, random_state=123)
adbr_3 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=100, random_state=123)

# 拟合上述三个模型
adbr_1.fit(X, y)
adbr_2.fit(X, y)
adbr_3.fit(X, y)

# 读取各个模型的最大迭代次数
adbr_1_n_estimators = adbr_1.get_params(True['n_estimators']
adbr_2_n_estimators = adbr_2.get_params(True['n_estimators']
adbr_3_n_estimators = adbr_3.get_params(True)['n_estimators']

# 预测
y_1 = adbr_1.predict(X)
y_2 = adbr_2.predict(X)
y_3 = adbr_3.predict(X)
# 画出各个模型的回归拟合效果
plt.figure(figsize=(10, 6))
# 画出训练数据集（用黑色表示）
plt.scatter(X, y, c="k", s=10, label="Training Samples")
# 画出adbr_1模型（最大迭代次数为1)的拟合效果（用红色表示）
plt.plot(X, y_1, c="r", label="n_estimators=%d" % adbr_1_n_estimators, linewidth=1)
# 画出adbr_2模型（最大迭代次数为10)的拟合效果（用绿色表示）
plt.plot(X, y_2, c="g", label="n_estimators=%d" % adbr_2_n_estimators, linewidth=1)
# 画出adbr_3模型（最大迭代次数为100)的拟合效果（用蓝色表示）
plt.plot(X, y_3, c="b", label="n_estimators=%d" % adbr_3_n_estimators, linewidth=1)

plt.xlabel("data")
plt.ylabel("target")
plt.title("AdaBoost_Regressor Comparison with different n_estimators when max_depth=3")
plt.legend()
plt.show()

输出结果如下：

可以看到，随着迭代次数的增加，AdaBoost回归器对数据的拟合效果变得越来越好，但是在迭代次数呈指数级增加的情况下，拟合效果并没有得到很明显的提升。由此可以推测，在基学习器的深度不够大的情况下，大幅增加迭代次数对缓解欠拟合的帮助并不大。接下来，我们尝试改变基学习器的最大深度，看看效果如何。

2 固定迭代次数

固定迭代次数为100，调节基学习器（回归决策树）的最大深度，分别为4、5、6，对比拟合效果。

代码如下：

# 拟合不同基学习器深度的回归模型
adbr_4 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=100, random_state=123)
adbr_5 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=5), n_estimators=100, random_state=123)
adbr_6 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=6), n_estimators=100, random_state=123)

# 拟合上述3个模型
adbr_4.fit(X, y)
adbr_5.fit(X, y)
adbr_6.fit(X, y)

# 预测
y_4 = adbr_4.predict(X)
y_5 = adbr_5.predict(X)
y_6 = adbr_6.predict(X)

# 画出各个模型的回归拟合效果
plt.figure(figsize=(10, 6))
# 画出训练数据集（用黑色表示）
plt.scatter(X, y, c="k", s=10, label="Training Samples")
# 画出adbr_4模型（基学习器深度为3)的拟合效果（用红色表示）
plt.plot(X, y_4, c="r", label="max_depth=4" , linewidth=1)
# 画出adbr_5模型（基学习器深度为4)的拟合效果（用绿色表示）
plt.plot(X, y_5, c="g", label="max_depth=5" , linewidth=1)
# 画出adbr_6模型（基学习器深度为5)的拟合效果（用蓝色表示）
plt.plot(X, y_6, c="b", label="max_depth=6" , linewidth=1)

plt.xlabel("data")
plt.ylabel("target")
plt.title("AdaBoost_Regressor Comparison with different max_depth when n_estimators=100")
plt.legend()
plt.show()

输出结果如下：

可以看到，在固定迭代次数为100的情况下，增加基学习器的最大深度对提升拟合效果的帮助非常大。所以，实际使用中，在控制拟合时间的前提下，读者应该尽量将基学习器回归决策树的最大深度设置得大一点，然后再在此基础上尝试对n_estimators等参数进行调参。