如有转载,请注明出处
常用激活函数列表
| name | plot | equation |
|---|---|---|
| sigmoid | 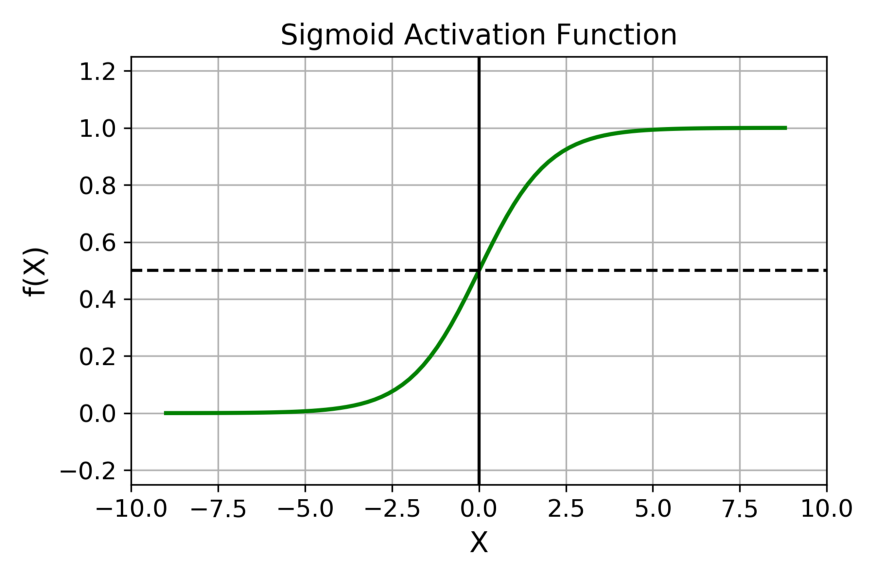 | f ( x ) = 1 1 + e − x f(x) = \frac{1}{1+e^{-x}} f(x)=1+e−x1 |
| Tanh | 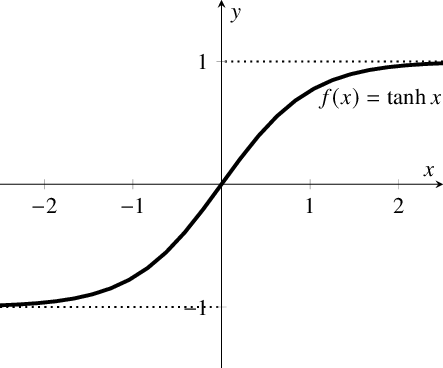 | f ( x ) = t a n h ( x ) = 2 1 + e − 2 x = 2 s i g m o i d ( 2 x ) − 1 f(x)=tanh(x)=\frac{2}{1+e^{-2x}} \\ = 2sigmoid(2x)-1 f(x)=tanh(x)=1+e−2x2=2sigmoid(2x)−1 |
| ReLU | 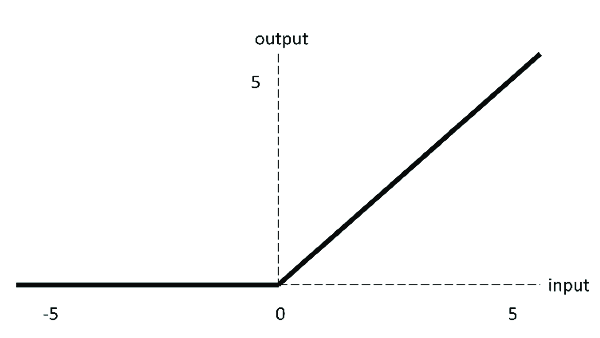 | f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x) |
| Leaky ReLU | 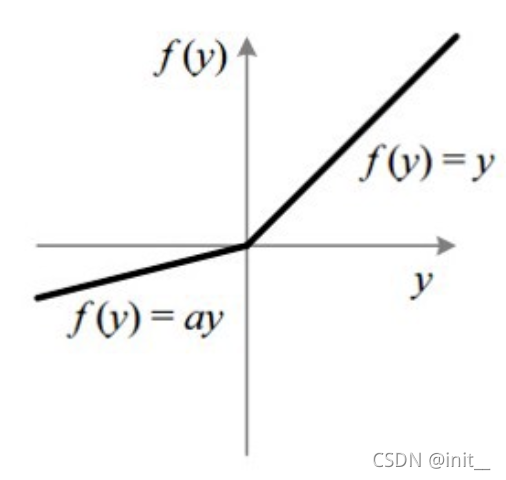 | 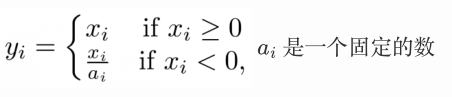 |
| PReLU | 可以看作是Leaky ReLU的一个变体。在PReLU中,负值部分的斜率是根据数据来定的 | |
| RReLU |  | RReLU也是Leaky ReLU的一个变体。在RReLU中,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。RReLU的亮点在于,在训练环节中, a j i a_{ji} aji是从一个均匀的分布U(I,u)中随机抽取的数值。 |
| ELU | 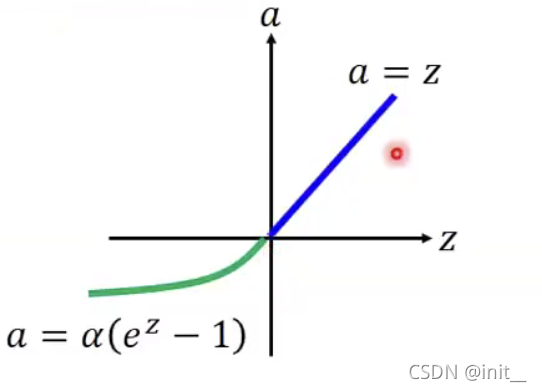 | |
| SELU | 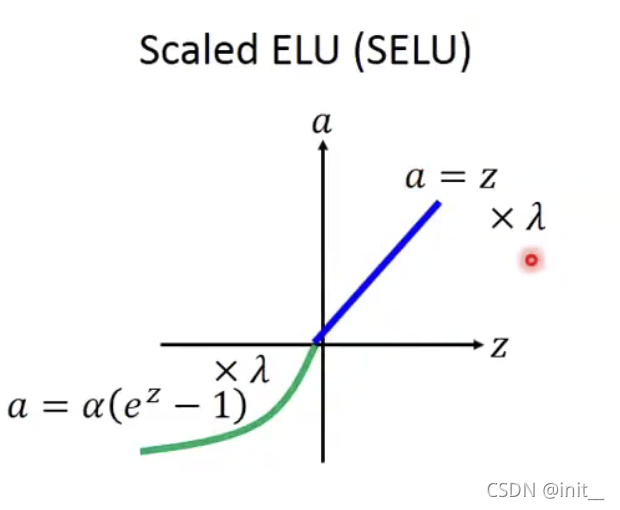 | ELU的变体,提供了 α \alpha α和 λ \lambda λ的值。具体可见论文作者的GitHub |
| Swish | 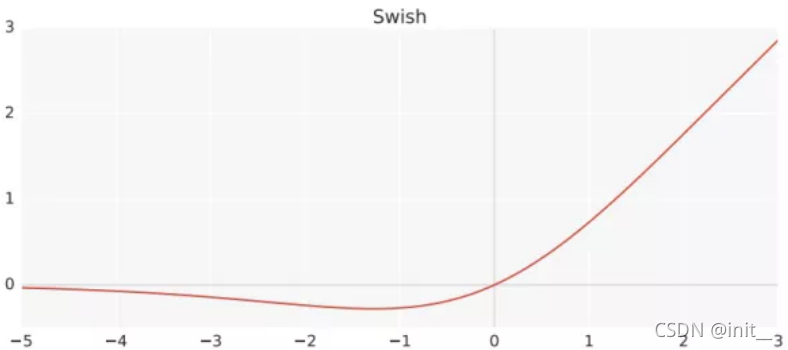 | s w i s h ( x ) = x ⋅ σ ( x ) swish(x) = x \cdot \sigma (x) swish(x)=x⋅σ(x) |
| Mish | 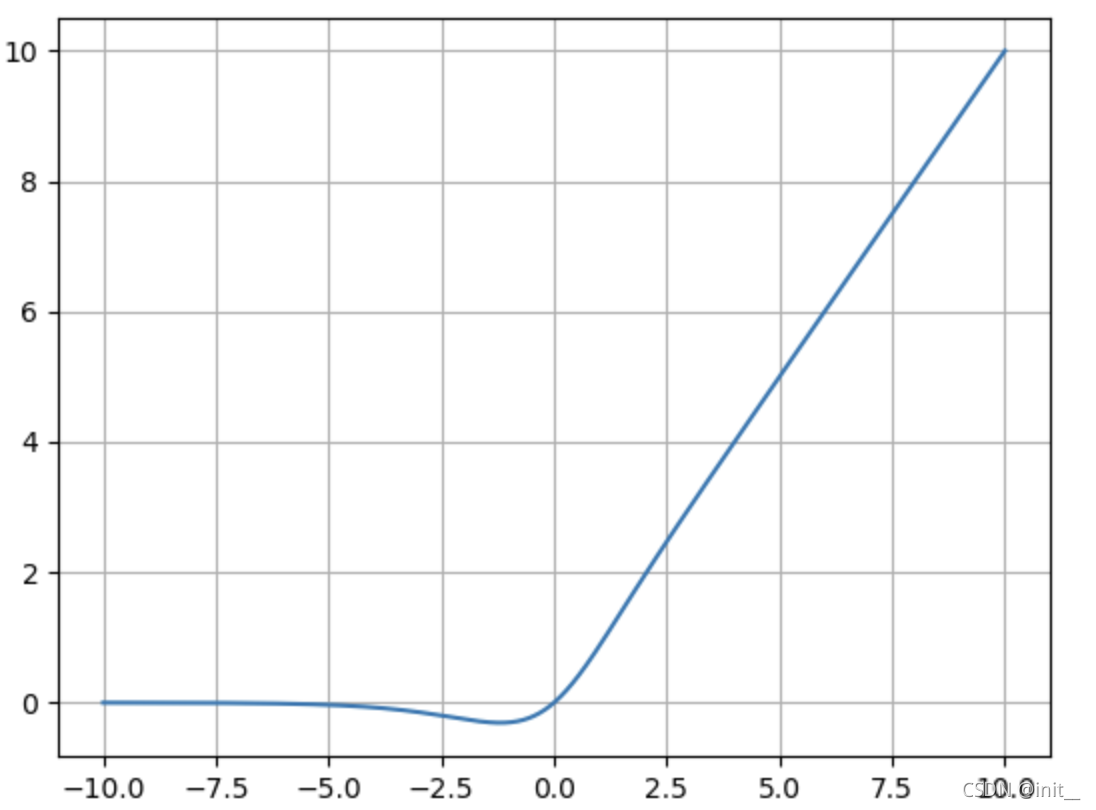 | m i s h ( x ) = x ⋅ t a n h ( s o f t p l u s ( x ) ) mish(x)= x \cdot tanh(softplus(x)) mish(x)=x⋅tanh(softplus(x)) |
常用激活函数介绍
sigmoid
早期的激活函数大多采用sigmoid函数,但是它存在一些问题:
- 过大或者过小的结果都会导致梯度趋近于0,再经过多层,梯度还会进行N次方操作,其结果就更小。这很容易就导致梯度弥散。这也是早期的神经网络都不深的原因。
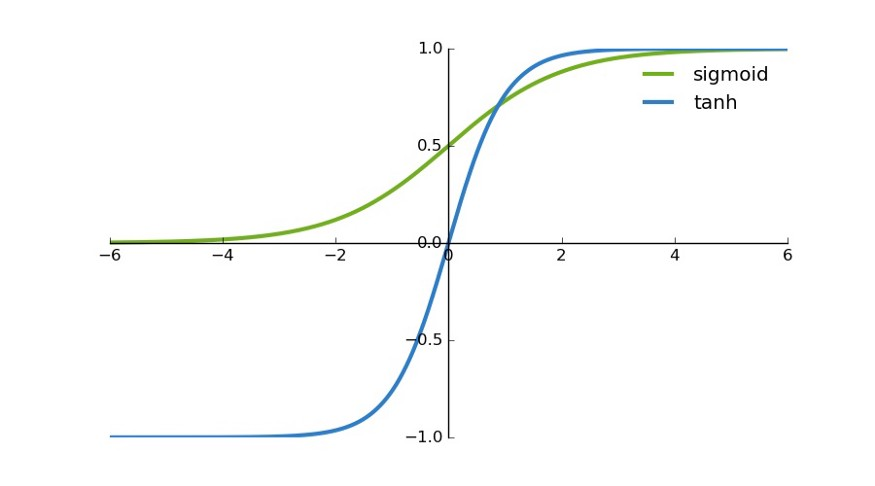
- 相比于tanh。可以看出sigmoid 的 区间为(0, 1);tanh的区间为(-1, 1)。sigmoid 会 使得结果一直为正。那么在反向传播时,经过同一个神经元传播而来的,多个参数的梯度总是同号的。其梯度的方向取决于同一个数,(如果是二维的)其梯度应在一三象限内移动,如果初始位置不佳,很容易导致zigzag。具体内容可参阅在神经网络中,激活函数sigmoid和tanh除了阈值取值外有什么不同吗?
ReLU
由于sigmoid、tanh的饱和区导数为0,导致网络不能做的很深。而ReLU的诞生,一定程度上解决了网络深度的问题。ReLU是分段线性函数,其非线性性很弱,因此网络一般都需要做的比较深。而这正迎合了当今的需求,在同样效果的前提下,往往深度比宽度更重要,更深的模型泛化能力更好。是当今最常用的激活函数。
ReLU 在 x < 0 x < 0 x<0 时,其梯度为0,会导致Dead ReLu的问题。而Leaky ReLU/PReLU/RReLU都是ReLU的变体,都是使得 x < 0 x<0 x<0时给他较小的梯度,解决了Dead ReLu的问题,但在实际操作中,尚未能证明,leaky RELU总是优于RELU。
SELU
Scaled ELU(SELU)形式上与ELU类似,只是增加了
α
\alpha
α的定义和增加了
λ
\lambda
λ。其结果为:
α
=
1.6732632423543772848170429916717
λ
=
1.0507009873554804934193349852946
\alpha = 1.6732632423543772848170429916717 \\ \lambda= 1.0507009873554804934193349852946
α=1.6732632423543772848170429916717λ=1.0507009873554804934193349852946
那么这两个数值是如何计算的呢?
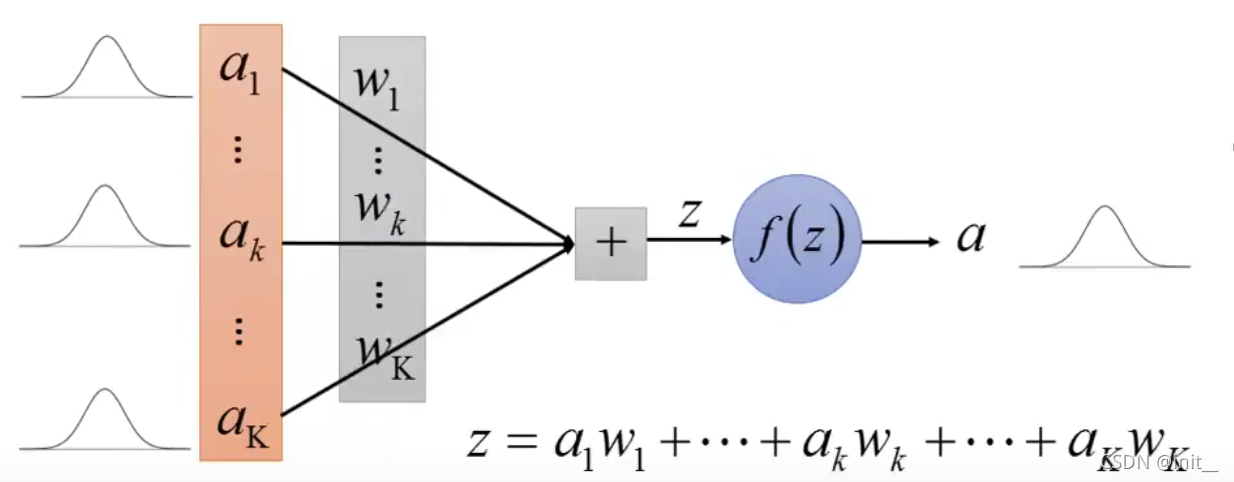
假设inputs是i.i.d的,且均值
μ
=
0
\mu =0
μ=0,方差
σ
2
=
1
\sigma^2 = 1
σ2=1;并假设参数的均值也是0。且inputs的分布可以为非高斯分布。
目标是:经过active function后,得到的结果的均值也是0,方差也是1。
对于
z
z
z,我们有:
μ
z
=
E
[
z
]
=
∑
k
=
1
K
E
(
a
k
)
w
k
=
0
\mu_z = E[z] = \sum_{k=1}^K E(a_k)w_k = 0
μz=E[z]=k=1∑KE(ak)wk=0
σ
z
2
=
E
[
(
z
−
μ
z
)
2
]
=
E
[
z
2
]
\sigma_z^2 = E[(z-\mu_z)^2]=E[z^2]
σz2=E[(z−μz)2]=E[z2]
其中含有两个部分,一个是:
E
[
(
a
k
w
k
)
2
]
=
w
k
2
E
[
a
k
2
]
=
w
k
2
σ
2
E[(a_kw_k)^2]=w_k^2E[a_k^2]=w_k^2\sigma^2
E[(akwk)2]=wk2E[ak2]=wk2σ2
E
[
a
i
a
j
w
i
w
j
]
=
w
i
w
j
E
[
a
i
]
E
[
a
j
]
=
0
E[a_ia_jw_iw_j]=w_iw_jE[a_i]E[a_j]=0
E[aiajwiwj]=wiwjE[ai]E[aj]=0
因此:
E
(
z
2
)
=
∑
w
k
2
σ
2
=
σ
2
K
σ
w
2
E(z^2)=\sum w_k^2\sigma^2=\sigma^2 K\sigma_w^2
E(z2)=∑wk2σ2=σ2Kσw2
令
K
⋅
σ
2
=
1
K \cdot \sigma^2=1
K⋅σ2=1,有
E
[
z
2
]
=
1
E[z^2]=1
E[z2]=1
由此可以假设, z z z是一个均值是0,方差为1的高斯分布。
中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布。
因此,当inputs的数量足够多时,可以满足正态分布。
再之后就是从 z z z去推导经过active function 得到一个均值是0,方差是1的结果。(由于数学公式太冗长,我也懒得再看了,btw,经过推导之后就可以求得两个参数的值)。
Swish 与 Mish
Swish , mish 的plot都类似,在神经网络中取得了优于RELU的效果,但是背后的原因目前没有理论和实验的证明。
参考苏剑林大神的说法:
-
Swish,mish在0点处是可微分的,且在0附近均有一定的梯度信息,在远小于0处其梯度结果为0
-
Xavier、Kaiming初始化都是在0附近的正态分布或均匀分布。如果使用ReLu会导致一半的参数梯度为0
参考
SELU
SELU 论文