JDK 8 中的 HashMap 是用数组+链表+红黑树实现的,我们要想往 HashMap 中放数据或者取数据,就需要确定数据在数组中的下标。
先把数据的键进行一次 hash:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
再做一次取模运算确定下标:
i = (n - 1) & hash
哈希表这样的数据结构容易产生两个问题:
- 数组的容量过小,经过哈希计算后的下标,容易出现冲突;
- 数组的容量过大,导致空间利用率不高。
加载因子是用来表示 HashMap 中数据的填满程度:
加载因子 = 填入哈希表中的数据个数 / 哈希表的长度
这就意味着:
- 加载因子越小,填满的数据就越少,哈希冲突的几率就减少了,但浪费了空间,而且还会提高扩容的触发几率;
- 加载因子越大,填满的数据就越多,空间利用率就高,但哈希冲突的几率就变大了。
好难!!!!
这就必须在“哈希冲突”与“空间利用率”两者之间有所取舍,尽量保持平衡,谁也不碍着谁。
我们知道,HashMap 是通过拉链法来解决哈希冲突的。
为了减少哈希冲突发生的概率,当 HashMap 的数组长度达到一个临界值的时候,就会触发扩容(可以点击链接查看 HashMap 的扩容机制),扩容后会将之前小数组中的元素转移到大数组中,这是一个相当耗时的操作。
这个临界值由什么来确定呢?
临界值 = 初始容量 * 加载因子
一开始,HashMap 的容量是 16:
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
加载因子是 0.75:
static final float DEFAULT_LOAD_FACTOR = 0.75f;
也就是说,当 16*0.75=12 时,会触发扩容机制。
为什么加载因子会选择 0.75 呢?为什么不是0.8、0.6呢?
这跟统计学里的一个很重要的原理——泊松分布有关。
是时候上维基百科了:
泊松分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松在1838年时提出。它会对随机事件的发生次数进行建模,适用于涉及计算在给定的时间段、距离、面积等范围内发生随机事件的次数的应用情形。
阮一峰老师曾在一篇博文中详细的介绍了泊松分布和指数分布,大家可以去看一下。
链接:https://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html
具体是用这么一个公式来表示的。
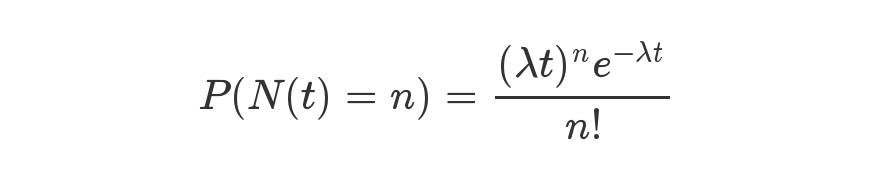
等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量。
在 HashMap 的 doc 文档里,曾有这么一段描述:
Because TreeNodes are about twice the size of regular nodes, we
use them only when bins contain enough nodes to warrant use
(see TREEIFY_THRESHOLD). And when they become too small (due to
removal or resizing) they are converted back to plain bins. In
usages with well-distributed user hashCodes, tree bins are
rarely used. Ideally, under random hashCodes, the frequency of
nodes in bins follows a Poisson distribution
(http://en.wikipedia.org/wiki/Poisson_distribution) with a
parameter of about 0.5 on average for the default resizing
threshold of 0.75, although with a large variance because of
resizing granularity. Ignoring variance, the expected
occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
factorial(k)). The first values are:
0: 0.60653066
1: 0.30326533
2: 0.07581633
3: 0.01263606
4: 0.00157952
5: 0.00015795
6: 0.00001316
7: 0.00000094
8: 0.00000006
more: less than 1 in ten million
大致的意思就是:
因为 TreeNode(红黑树)的大小约为链表节点的两倍,所以我们只有在一个拉链已经拉了足够节点的时候才会转为tree(参考TREEIFY_THRESHOLD)。并且,当这个hash桶的节点因为移除或者扩容后resize数量变小的时候,我们会将树再转为拉链。如果一个用户的数据的hashcode值分布得很均匀的话,就会很少使用到红黑树。
理想情况下,我们使用随机的hashcode值,加载因子为0.75情况,尽管由于粒度调整会产生较大的方差,节点的分布频率仍然会服从参数为0.5的泊松分布。链表的长度为 8 发生的概率仅有 0.00000006。
虽然这段话的本意更多的是表示 jdk 8中为什么拉链长度超过8的时候进行了红黑树转换,但提到了 0.75 这个加载因子——但这并不是为什么加载因子是 0.75 的答案。
为了搞清楚到底为什么,我看到了这篇文章:
参考链接:https://segmentfault.com/a/1190000023308658
里面提到了一个概念:二项分布(二哥概率论没学好,只能简单说一说)。
在做一件事情的时候,其结果的概率只有2种情况,和抛硬币一样,不是正面就是反面。
为此,我们做了 N 次实验,那么在每次试验中只有两种可能的结果,并且每次实验是独立的,不同实验之间互不影响,每次实验成功的概率都是一样的。
以此理论为基础,我们来做这样的实验:我们往哈希表中扔数据,如果发生哈希冲突就为失败,否则为成功。
我们可以设想,实验的hash值是随机的,并且经过hash运算的键都会映射到hash表的地址空间上,那么这个结果也是随机的。所以,每次put的时候就相当于我们在扔一个16面(我们先假设默认长度为16)的骰子,扔骰子实验那肯定是相互独立的。碰撞发生即扔了n次有出现重复数字。
然后,我们的目的是啥呢?
就是掷了k次骰子,没有一次是相同的概率,需要尽可能的大些,一般意义上我们肯定要大于0.5(这个数是个理想数,但是我是能接受的)。
于是,n次事件里面,碰撞为0的概率,由上面公式得:
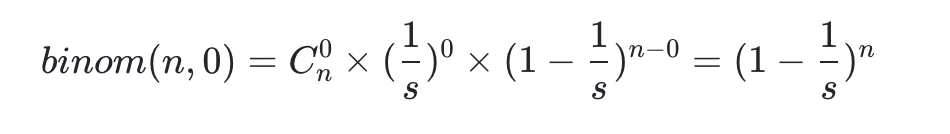
这个概率值需要大于0.5,我们认为这样的hashmap可以提供很低的碰撞率。所以:
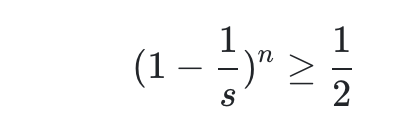
这时候,我们对于该公式其实最想求的时候长度s的时候,n为多少次就应该进行扩容了?而负载因子则是 n / s n/s n/s的值。所以推导如下:

所以可以得到
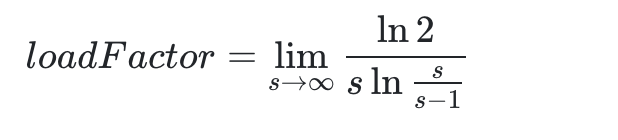
其中
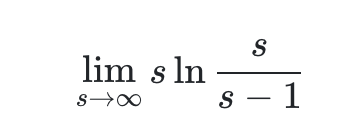
这就是一个求 ∞⋅0函数极限问题,这里我们先令
s
=
m
+
1
(
m
→
∞
)
s = m+1(m \to \infty)
s=m+1(m→∞)则转化为
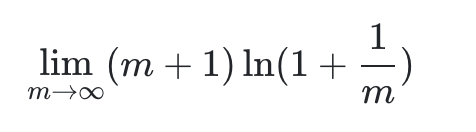
我们再令 x = 1 m ( x → 0 ) x = \frac{1}{m} (x \to 0) x=m1(x→0) 则有,

所以,
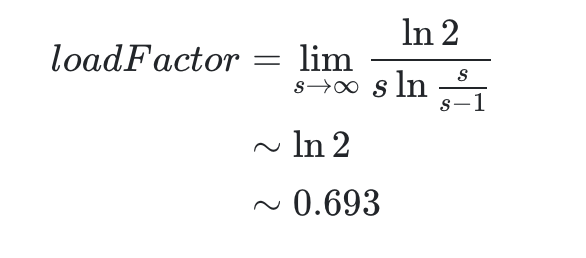
考虑到 HashMap的容量有一个要求:它必须是2的n 次幂(这个之前的文章讲过了,点击链接回去可以再温故一下)。当加载因子选择了0.75就可以保证它与容量的乘积为整数。
16*0.75=12
32*0.75=24
除了 0.75,0.5~1 之间还有 0.625(5/8)、0.875(7/8)可选,从中位数的角度,挑 0.75 比较完美。另外,维基百科上说,拉链法(解决哈希冲突的一种)的加载因子最好限制在 0.7-0.8以下,超过0.8,查表时的CPU缓存不命中(cache missing)会按照指数曲线上升。
综上,0.75 是个比较完美的选择。
本文 GitHub 上已同步,有 GitHub 账号的小伙伴,记得给二哥安排一波 star 呀!冲 GitHub 的 trending 榜单,求求各位了。
GitHub 地址:https://github.com/itwanger/toBeBetterJavaer