🌲本文收录于专栏《糊涂算法》——从今天起,迈过数据结构和算法这道坎
作者其它优质专栏推荐:
📚《技术专家修炼》——搞技术,进大厂,聊人生三合一专栏
📚《leetcode 300题》——每天一道算法题,进大厂必备
📚《源码中的设计模式》——理论与实战的完美结合
📚《从实战学python》——Python的爬虫,自动化,AI等实战应用(代码开源)
点击跳转到文末领取粉丝福利
哈喽,大家好,我是一条~
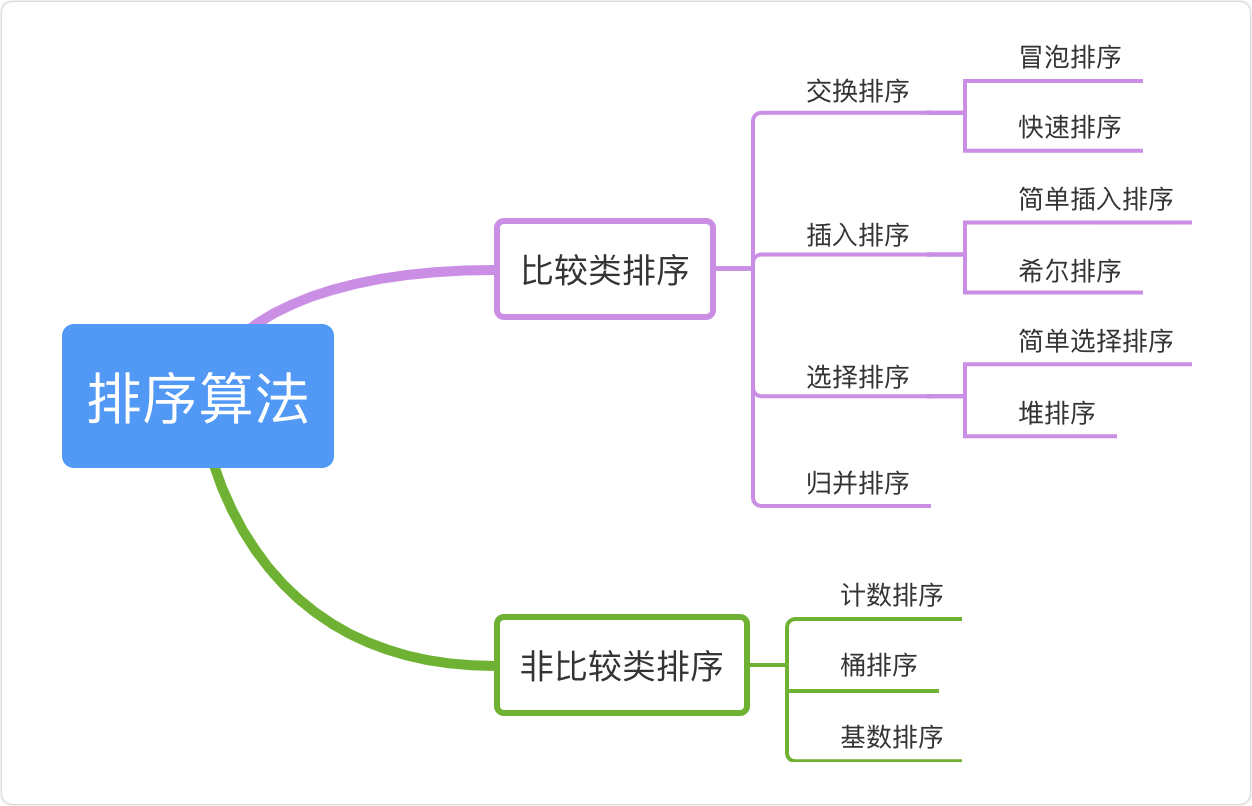
今天给大家带来《糊涂算法》专栏的第二期内容——排序算法的讲解。相信无论是初学者学习还是大厂面试,都少不了排序算法这关,即使没学过算法,对冒泡排序也不会陌生。
今天,一条就带大家彻底跨过「排序算法」这道坎,保姆级教程建议收藏。⭐️
本文配套源码地址:《八大排序》源码,提取码:5ehp
准备
古语云:“兵马未动,粮草先行”。想跟着一条一块把「排序算法」弄明白的,建议先准备好以下代码模板。
📢 观看本教程需知道基本循环语法、两数交换、双指针等前置知识。
📚 建议先看完代码和逐步分析后再尝试自己写。
- 新建一个
Java工程,本文全篇也基于Java语言实现代码。 - 建立如下目录结构
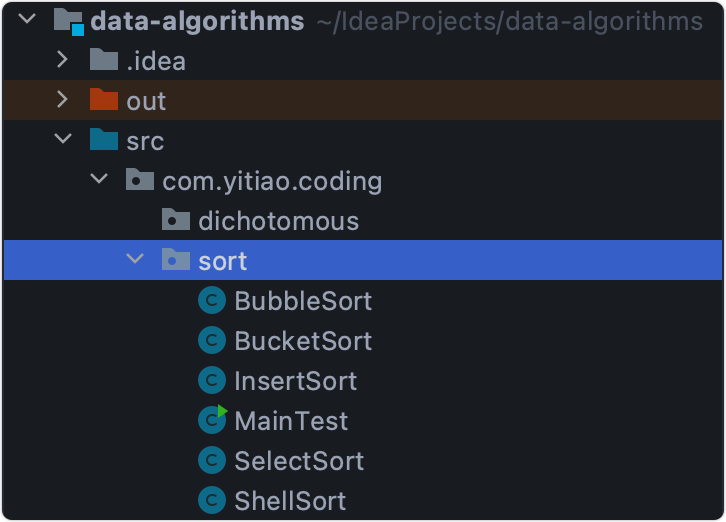
- 在
MainTest测试类中编写测试模板。
/**
* 测试类
* Author:一条
* Date:2021/09/23
*/
public class MainTest {
public static void main(String[] args) {
//待排序序列
int[] array={6,10,4,5,2,8};
//调用不同排序算法
// BubbleSort.sort(array);
// 创建有100000个随机数据的数组
int[] costArray=new int[100000];
for (int i = 0; i < 100000; i++) {
// 生成一个[0,100000) 的一个数
costArray[i] = (int) (Math.random() * 100000);
}
Date start = new Date();
//过长,先注释掉逐步打印
//BubbleSort.sort(costArray);
Date end = new Date();
System.out.println("耗时:"+(end.getTime()-start.getTime())/1000+"s");
}
}
该段代码内容主要有两个功能:
- 调用不同的排序算法进行测试
- 测试不同排序算法将
10w个数排好序需要的时间。更加具象的理解时间复杂度的不同
冒泡排序
基本思想
通过对乱序序列从前向后遍历,依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部。
像水底下的气泡一样逐渐向上冒一样。

动图讲解
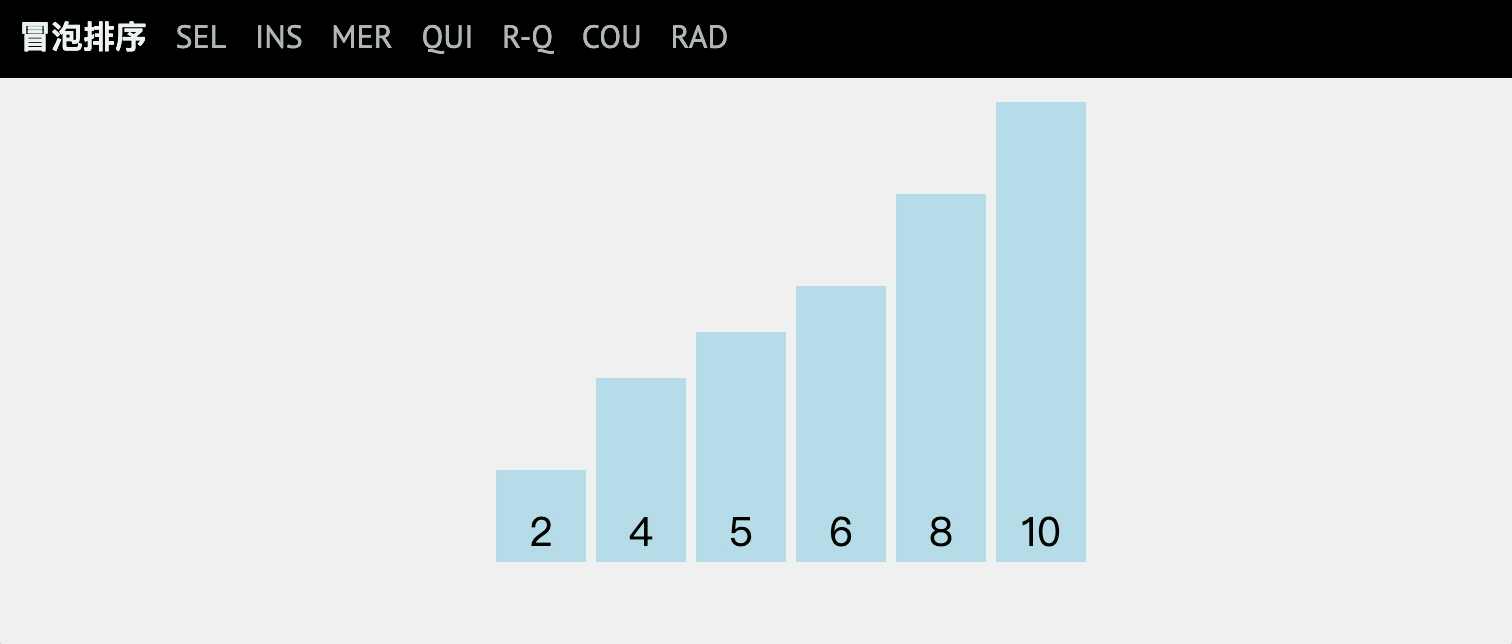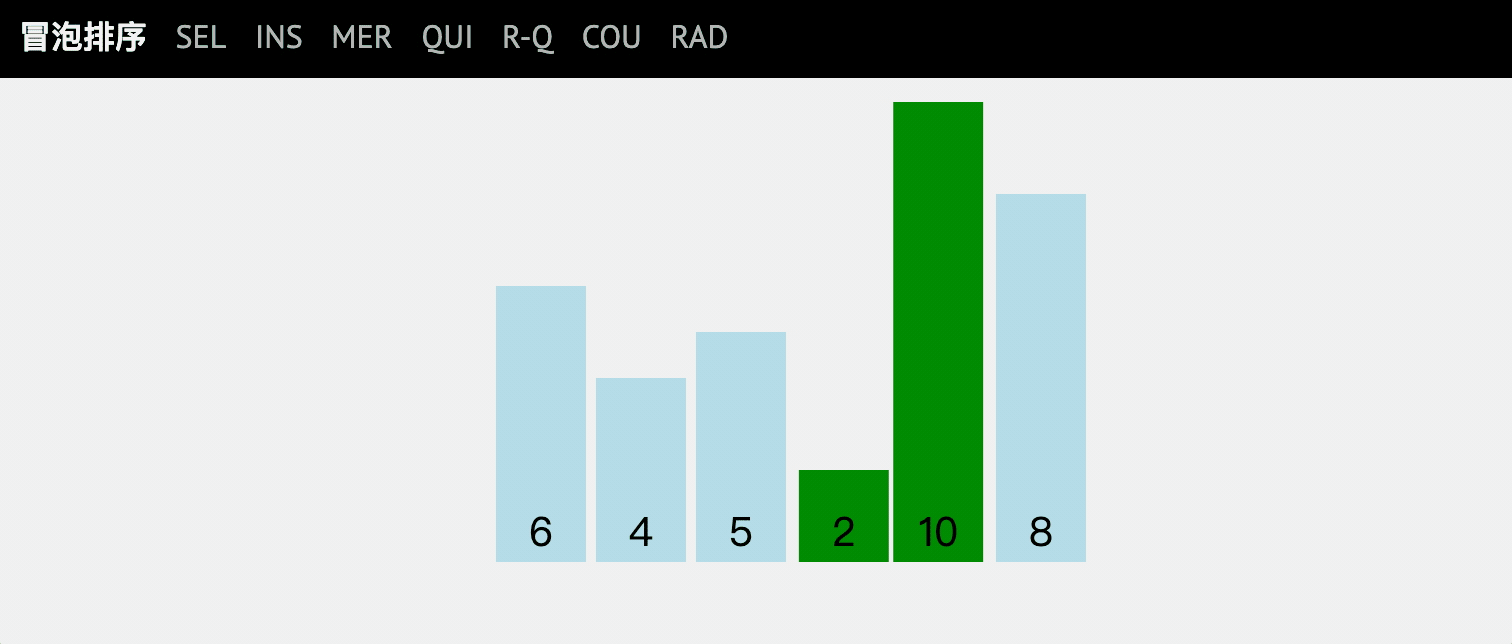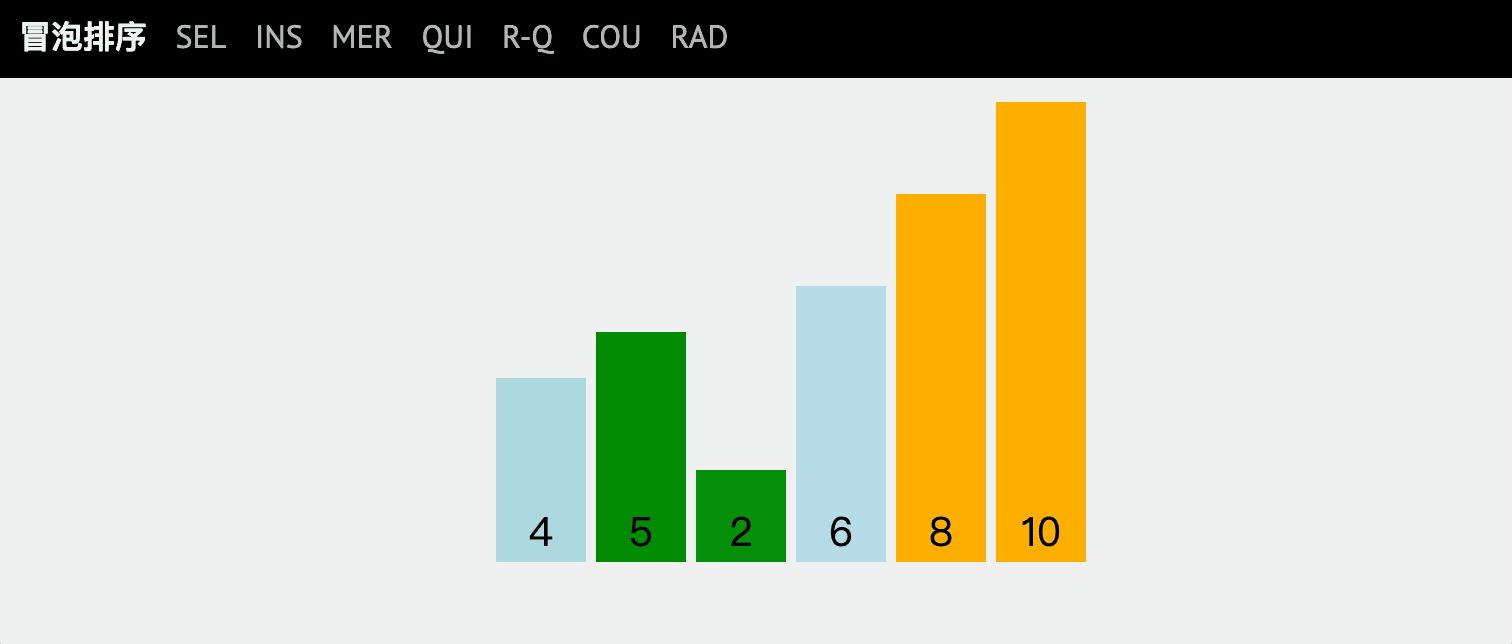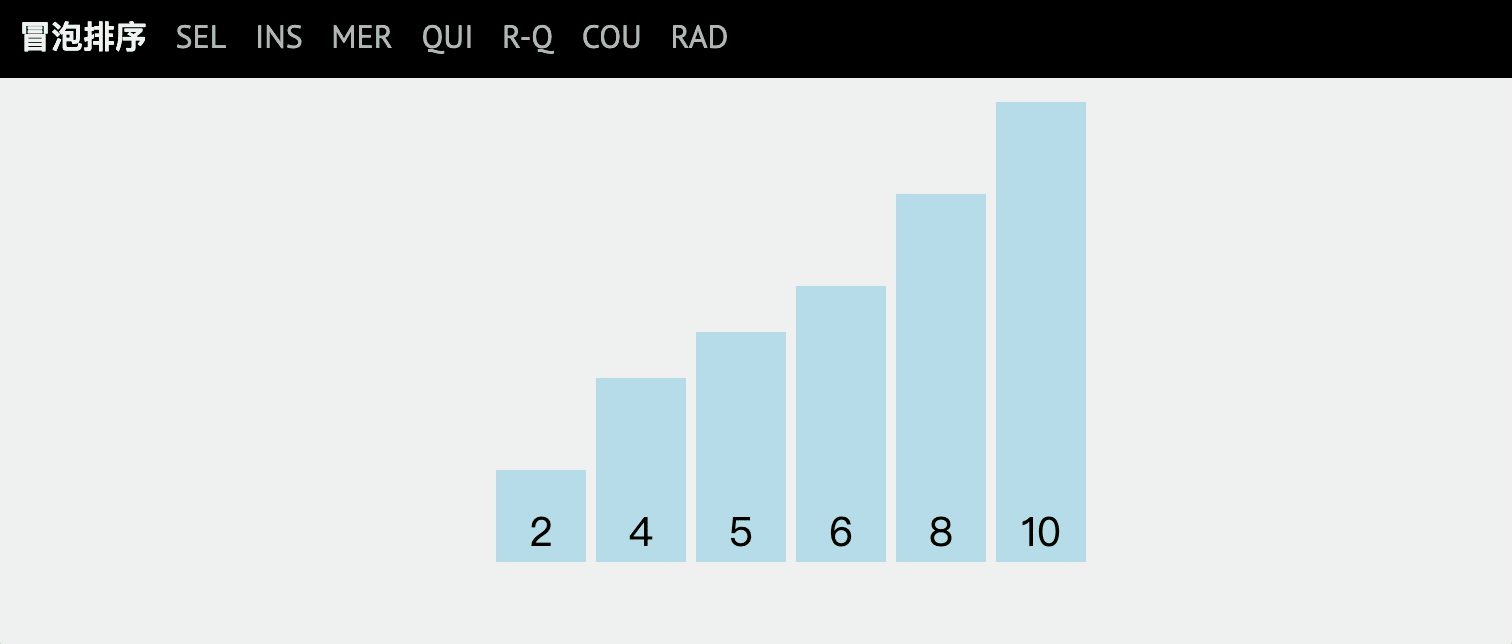
代码实现
不理解的小伙伴可以用
debug模式逐步分析。
/**
* 冒泡排序
* Author:一条
* Date:2021/09/23
*/
public class BubbleSort{
public static int[] sort(int[] array){
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length-1; j++) {
//依次比较,将最大的元素交换到最后
if (array[j]>array[j+1]){
// 用临时变量temp交换两个值
int temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
//输出每一步的排序结果
System.out.println(Arrays.toString(array));
}
return array;
}
}
输出结果
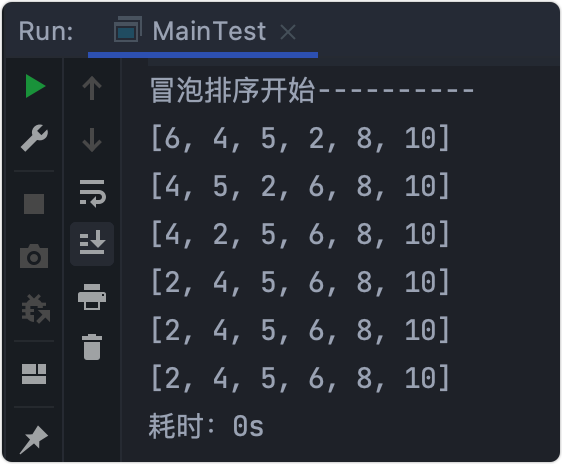
逐步分析
- 初始数组:
[6,10,4,5,2,8] 6拿出来和后一个10比较,6<10,不用交换。- >j++;10拿出来和后一个4比较,10>4,交换。- >[6,4,10,5,2,8]- 依次执行
j++与后一个比较交换。 - 第一层
i循环完,打印第一行- >[6, 4, 5, 2, 8, 10],此时最后一位10在正确位置上。 - >i++ - 从
4开始,继续比较交换,倒数第二位8回到正确位置。 - 如上循环下去 - > ……
- 最终结果 - >
[2, 4, 5, 6, 8, 10]
这时再回去看动图理解。
耗时测试
记得先注释掉排序类逐步打印代码。
时间复杂度:O(n^2)
算法优化
优化点一
外层第一次遍历完,最后一位已经是正确的,j就不需要再比较,所以结束条件应改为j-i-1;。
优化点二
因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。
优化代码
public static int[] sortPlus(int[] array){
System.out.println("优化冒泡排序开始----------");
for (int i = 0; i < array.length; i++) {
boolean flag=false;
for (int j = 0; j < array.length-i-1; j++) {
if (array[j]>array[j+1]){
flag=true;
int temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
if (flag==false){
break;
}
// System.out.println(Arrays.toString(array));
}
return array;
}
优化测试
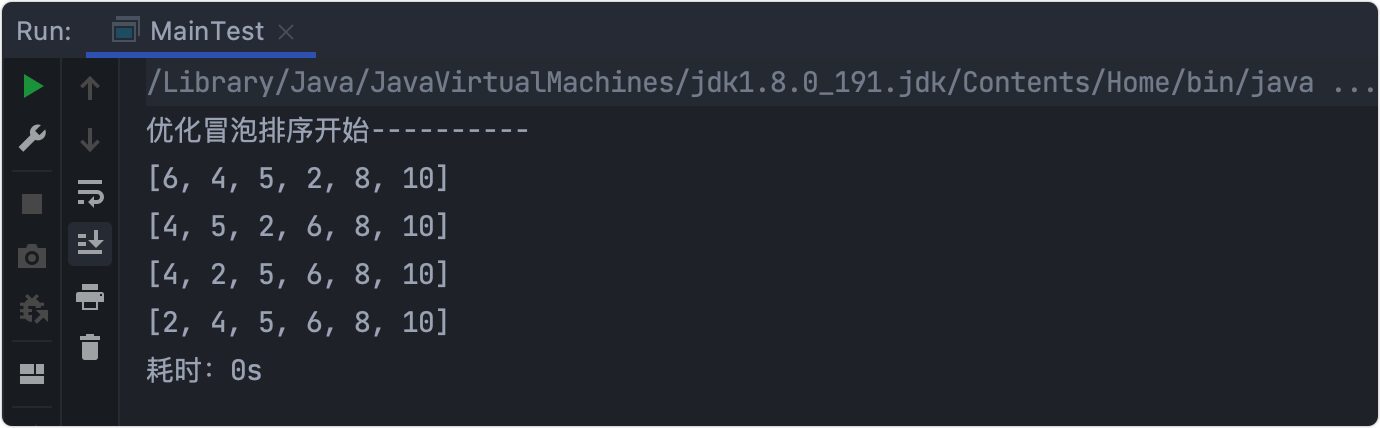
通过基础测试看到当序列已经排好序,即不发生交换后终止循环。
耗时测试由27s优化到17s。
选择排序
基本思想
选择排序和冒泡排序很像,是从乱序序列的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。
动图讲解

代码实现
public class SelectSort {
public static int[] sort(int[] array) {
System.out.println("选择排序开始----------");
for (int i = 0; i < array.length; i++) {
//每个值只需与他后面的值进行比较,所以从开始
for (int j = i; j < array.length; j++) {
//注意此处是哪两个值比较
if (array[i]>array[j]){
int temp=array[i];
array[i]=array[j];
array[j]=temp;
}
}
System.out.println(Arrays.toString(array));
}
return array;
}
}
输出结果
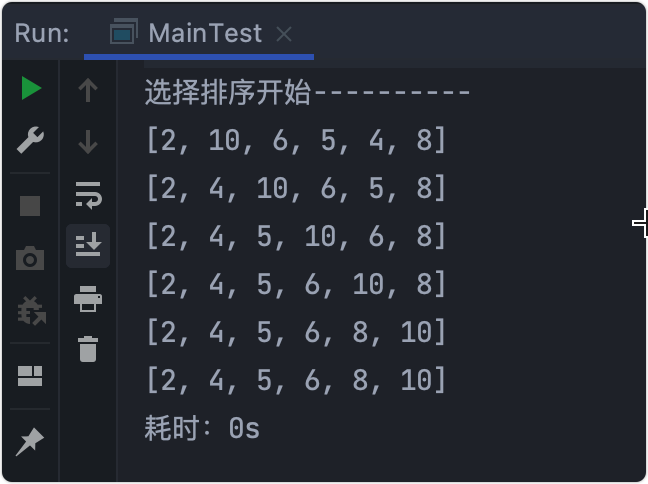
逐步分析
- 初始数组:
[6,10,4,5,2,8] - 拿出
6与10比较,不交换 - >j++ 6与2比较,交换 - >j++- 注意此时是拿
2继续比较,都不交换,确定第一位(最小的数)为2- >i++ - 循环下去,依次找到第一小,第二小,……的数
- 最终结果 - >
[2, 4, 5, 6, 8, 10]
这时再回去看动图理解。
耗时测试
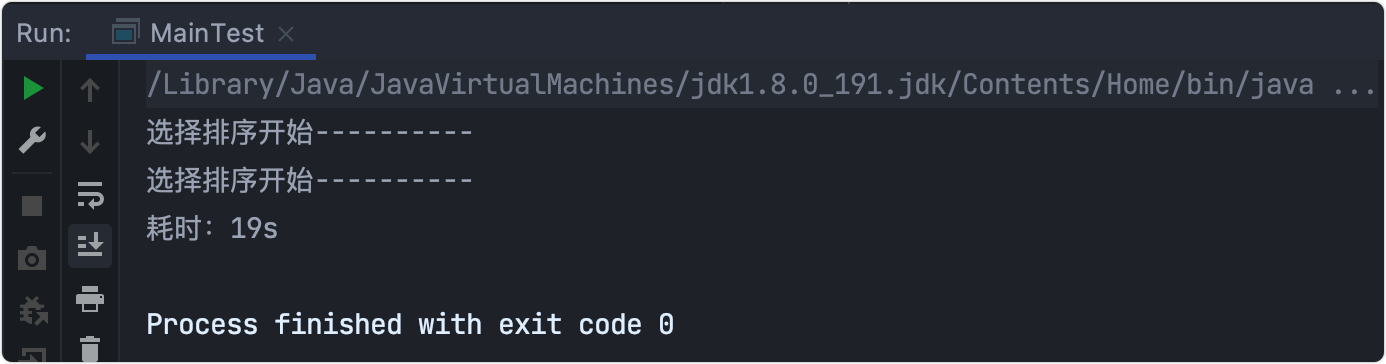
时间复杂度:O(n^2)
算法优化
上诉代码中使用交换的方式找到较小值,还可以通过移动的方式,即全部比较完只交换一次。
这种对空间的占有率会有些增益,但对时间的增益几乎没有,可忽略,亦不再演示。
插入排序
基本思想
把n个乱序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中通过不断往有序表插入元素,获取一个局部正确解,逐渐扩大有序序列的长度,直到完成排序。
动图讲解

代码实现
/**
* 插入排序
* Author:一条
* Date:2021/09/23
*/
public class InsertSort {
public static void sort(int[] array) {
for (int i = 1; i < array.length; i++) {
//插入有序序列,且将有序序列扩大
for (int j = i; j > 0; j--) {
if (array[j]>array[j-1]){
int temp=array[j];
array[j]=array[j-1];
array[j-1]=temp;
}
}
// System.out.println(Arrays.toString(array));
}
}
}
输出结果
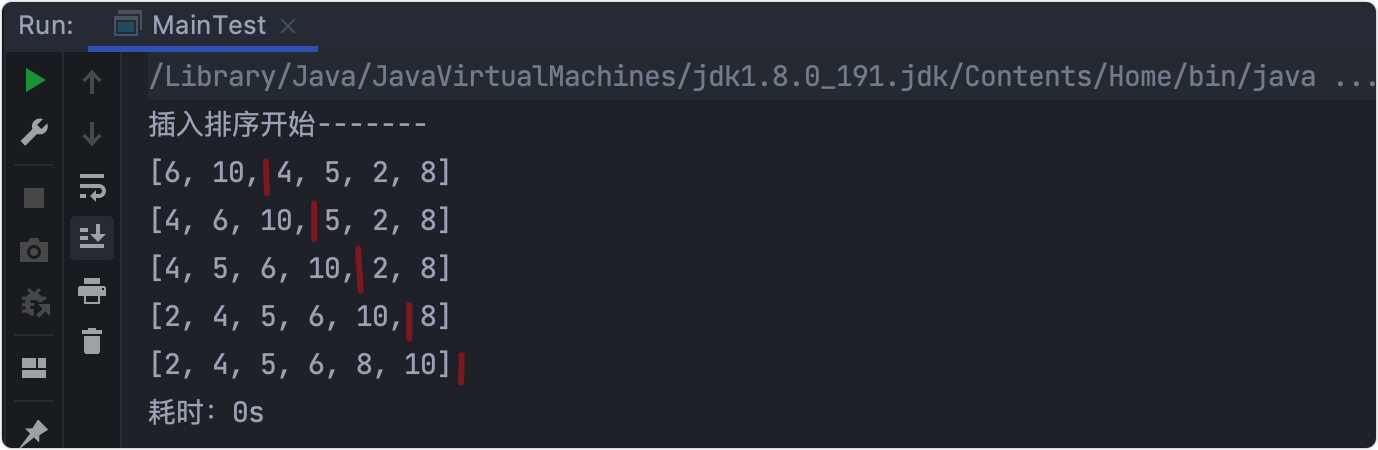
耗时测试
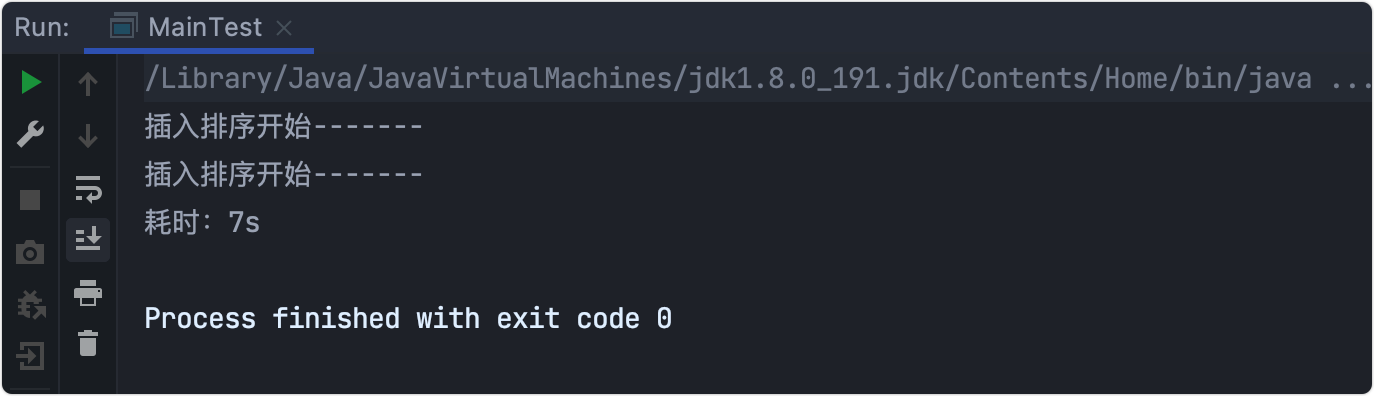
算法优化
见下方希尔排序,就是希尔对插入排序的优化。
希尔排序
希尔排序是插入排序的一个优化,思考往
[2,3,4,5,6]中插入1,需要将所有元素的位置都移动一遍,也就是说在某些极端情况下效率不高,也称该算法不稳定。希尔排序是插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
基本思想
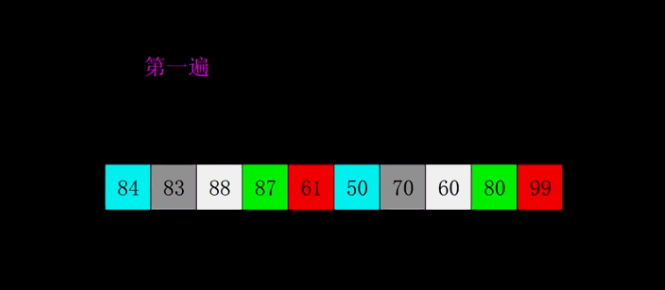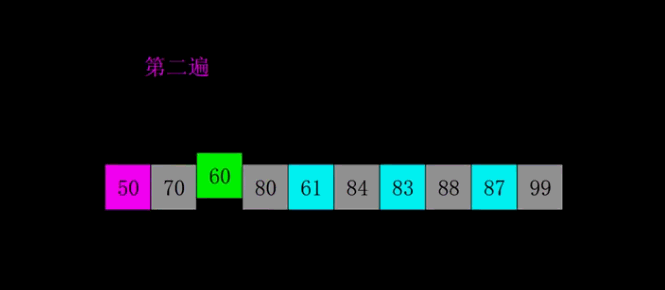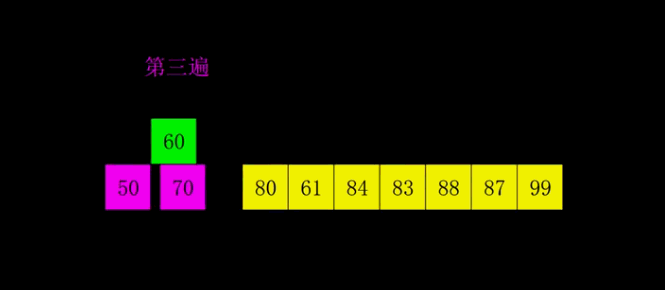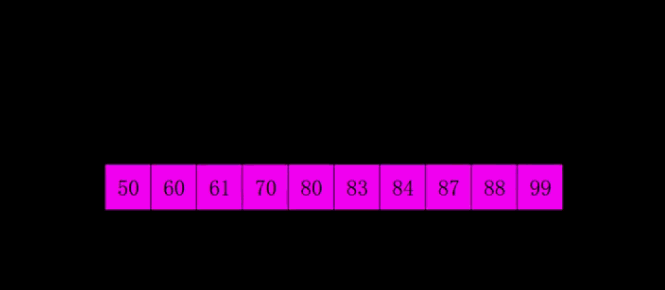
希尔排序是把记录按下标的一定增量分组,对每组使用插入排序;
随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个序列恰被分成一组,算法便终止。
和插入排序一样,从局部到全部,希尔排序是局部再局部。
动图讲解
代码实现
/**
* 希尔排序
* Author:一条
* Date:2021/09/23
*/
public class ShellSort {
public static void sort(int[] array) {
System.out.println("希尔排序开始--------");
//gap初始增量=length/2 逐渐缩小:gap/2
for (int gap = array.length/2; gap > 0 ; gap/=2) {
//插入排序 交换法
for (int i = gap; i < array.length ; i++) {
int j = i;
while(j-gap>=0 && array[j]<array[j-gap]){
//插入排序采用交换法
int temp = array[j];
array[j]=array[j-gap];
array[j-gap]=temp;
j-=gap;
}
}
System.out.println(Arrays.toString(array));
}
}
}
输出结果
耗时测试
算法优化
无
快速排序
快速排序(Quicksort)是对冒泡排序的一种改进,相比冒泡排序,每次的交换都是跳跃式的。
基本思想
将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
体现出分治的思想。
动图讲解
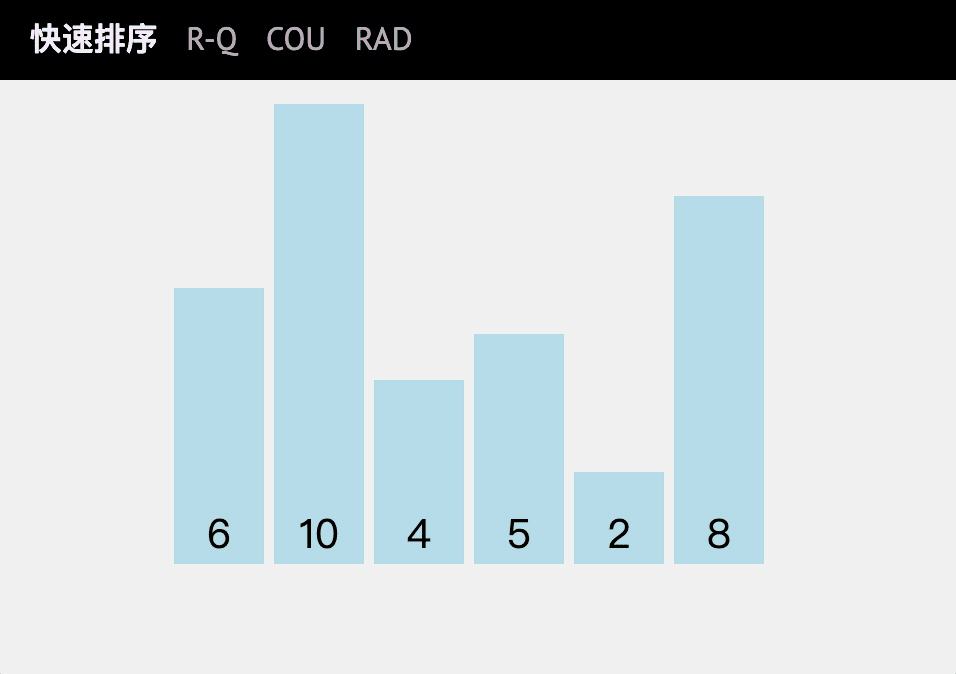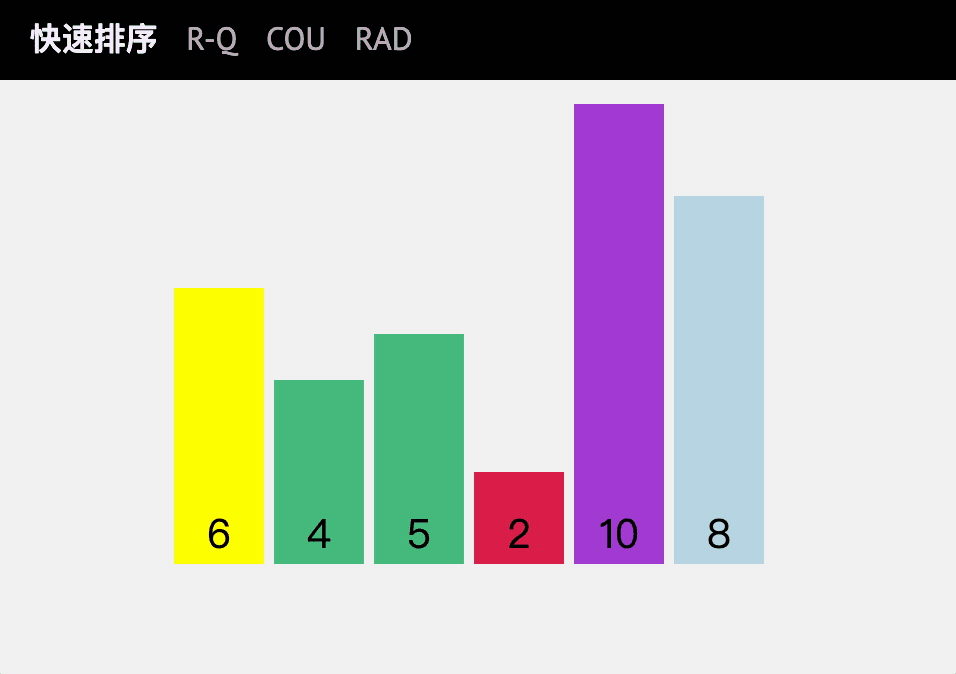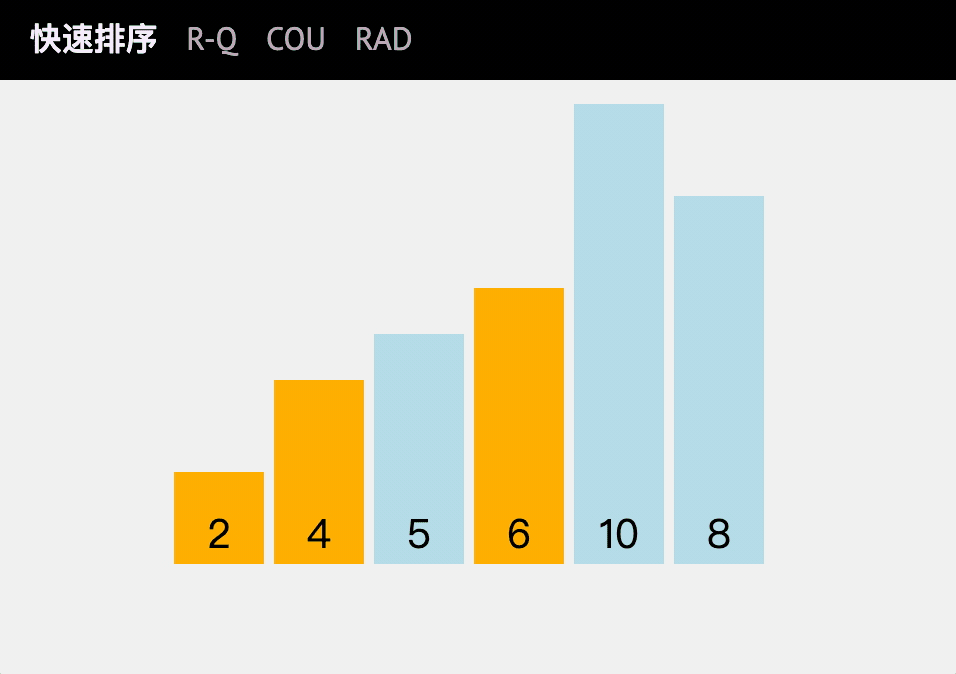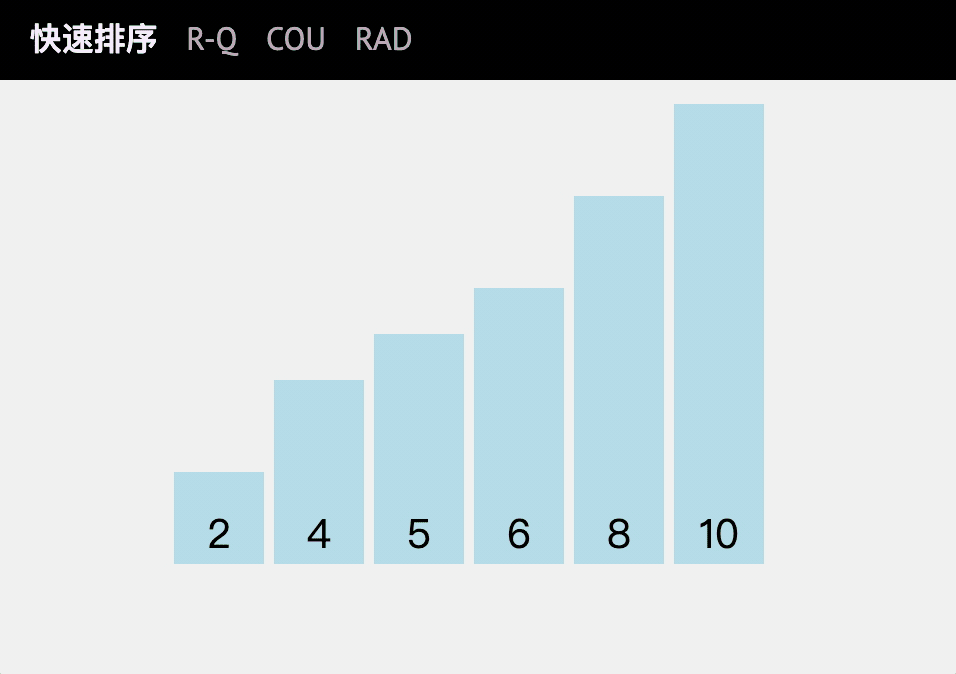
代码实现
思路如下:
- 首先在这个序列中找一个数作为基准数,为了方便可以取第一个数。
- 遍历数组,将小于基准数的放置于基准数左边,大于基准数的放置于基准数右边。此处可用双指针实现。
- 此时基准值把数组分为了两半,基准值算是已归位(找到排序后的位置)。
- 利用递归算法,对分治后的子数组进行排序。
public class QuickSort {
public static void sort(int[] array) {
System.out.println("快速排序开始---------");
mainSort(array, 0, array.length - 1);
}
private static void mainSort(int[] array, int left, int right) {
if(left > right) {
return;
}
//双指针
int i=left;
int j=right;
//base就是基准数
int base = array[left];
//左边小于基准,右边大于基准
while (i<j) {
//先看右边,依次往左递减
while (base<=array[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
while (base>=array[i]&&i<j) {
i++;
}
//交换
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
//最后将基准为与i和j相等位置的数字交换
array[left] = array[i];
array[i] = base;
System.out.println(Arrays.toString(array));
//递归调用左半数组
mainSort(array, left, j-1);
//递归调用右半数组
mainSort(array, j+1, right);
}
}
输出结果
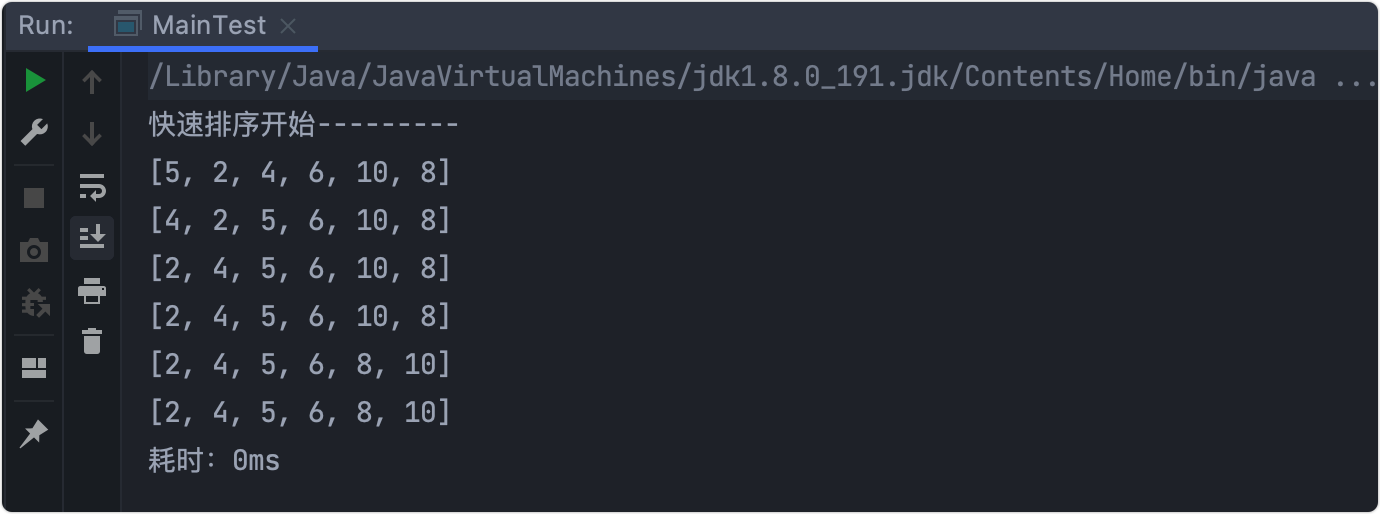
逐步分析
- 将
6作为基准数,利用左右指针使左边的数<6,右边的数>6。 - 对左右两边递归,即左边用
5作为基准数继续比较。 - 直到
left > right结束递归。
耗时测试
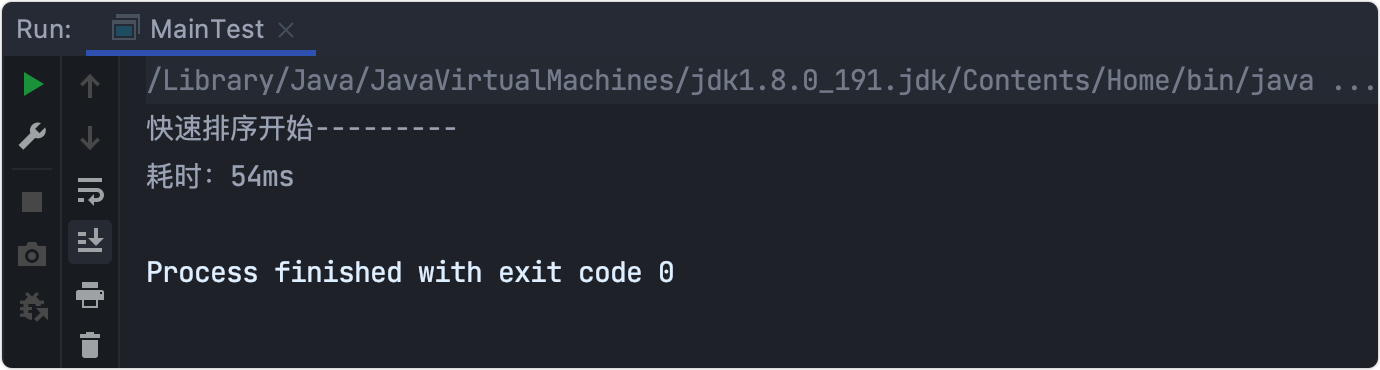
快速排序为什么这么快?
算法优化
优化一
三数取中(median-of-three):我们目前是拿第一个数作为基准数,对于部分有序序列,会浪费循环,可以用三数取中法优化,感性的小伙伴可自行了解。
优化二
快速排序对于长序列非常快,但对于短序列不如插入排序。可以综合使用。
堆排序
此章节对基础知识要求较高,初学者可跳过。
基本思想
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种**选择排序,**它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
主要利用堆顶元素最大或最小的特性,通过不断构建大顶堆,交换堆顶和堆尾,断尾重构的方式实现排序。
动图讲解

代码实现
public class HeapSort {
public static void sort(int[] array) {
//创建堆
for (int i = (array.length - 1) / 2; i >= 0; i--) {
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(array, i, array.length);
}
//调整堆结构+交换堆顶元素与末尾元素
for (int i = array.length - 1; i > 0; i--) {
//将堆顶元素与末尾元素进行交换
int temp = array[i];
array[i] = array[0];
array[0] = temp;
//重新对堆进行调整
adjustHeap(array, 0, i);
}
}
/**
* 调整堆
* @param array 待排序列
* @param parent 父节点
* @param length 待排序列尾元素索引
*/
private static void adjustHeap(int[] array, int parent, int length) {
//将temp作为父节点
int temp = array[parent];
//左孩子
int lChild = 2 * parent + 1;
while (lChild < length) {
//右孩子
int rChild = lChild + 1;
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (rChild < length && array[lChild] < array[rChild]) {
lChild++;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= array[lChild]) {
break;
}
// 把孩子结点的值赋给父结点
array[parent] = array[lChild];
//选取孩子结点的左孩子结点,继续向下筛选
parent = lChild;
lChild = 2 * lChild + 1;
}
array[parent] = temp;
System.out.println(Arrays.toString(array));
}
}
输出结果
逐步分析
- 构建初始堆,将待排序列构成一个大顶堆(或者小顶堆),升序大顶堆,降序小顶堆;
- 将堆顶元素与堆尾元素交换,并断开(从待排序列中移除)堆尾元素。
- 重新构建堆。
- 重复2~3,直到待排序列中只剩下一个元素(堆顶元素)。
耗时测试
算法优化
优化点关键就在于我们以什么手法找到顶部元素该有的位置,有兴趣同学可以继续研究。
归并排序
基本思想
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,采用经典的分治(divide-and-conquer)策略。
将乱序序列不断的分成一半,排好序再拼回去,用递归实现。
难点在于如何归并两个排好序的数组?
我们可以开辟一个临时数组,使用快慢指针来辅助我们的归并。
虽然需要额外空间的来完成这个排序。但是现在计算机的内存都比较大,时间的效率要比空间的效率重要的多。
所以空间换时间也是优化算法时的一个方向。
动图讲解
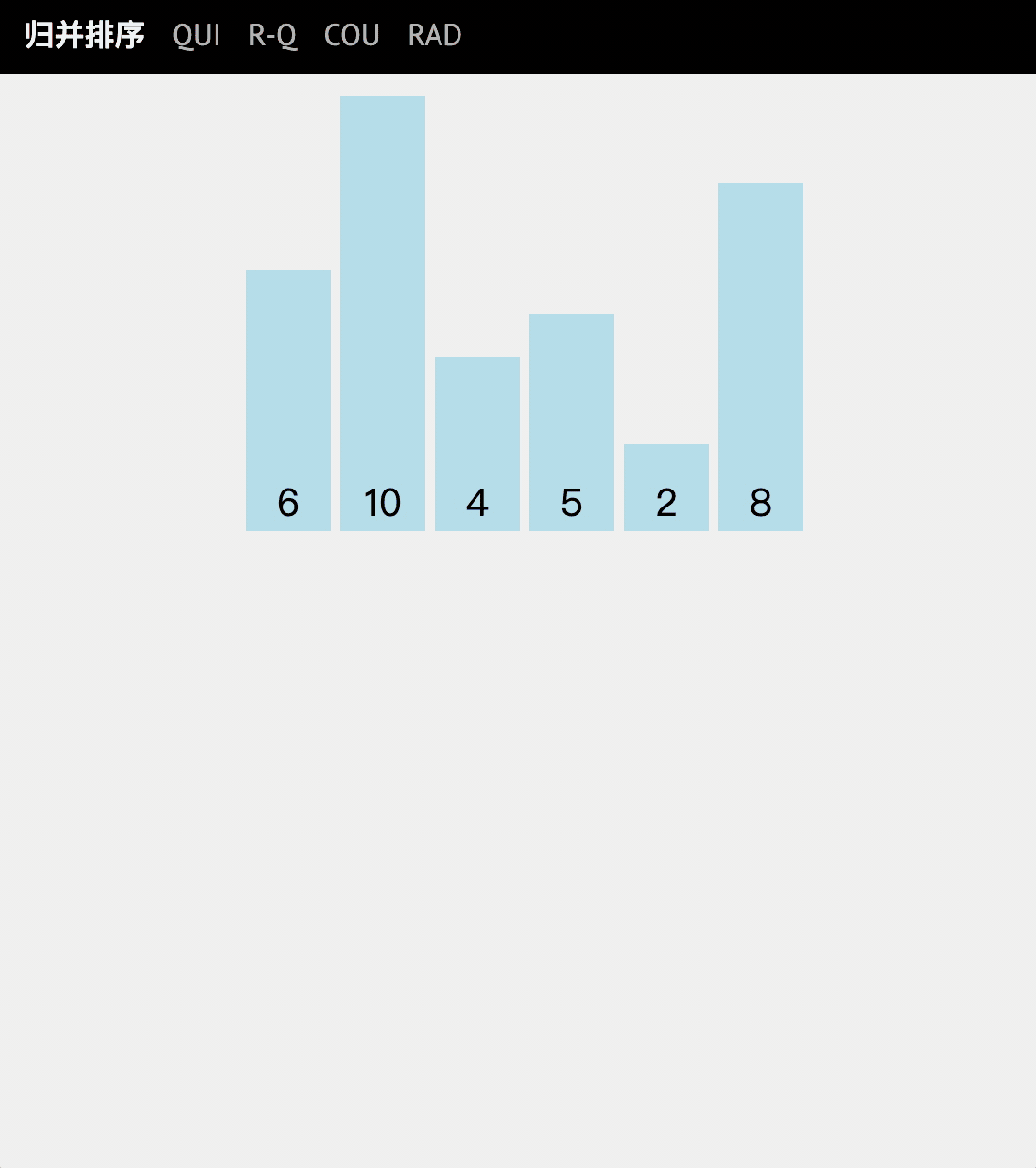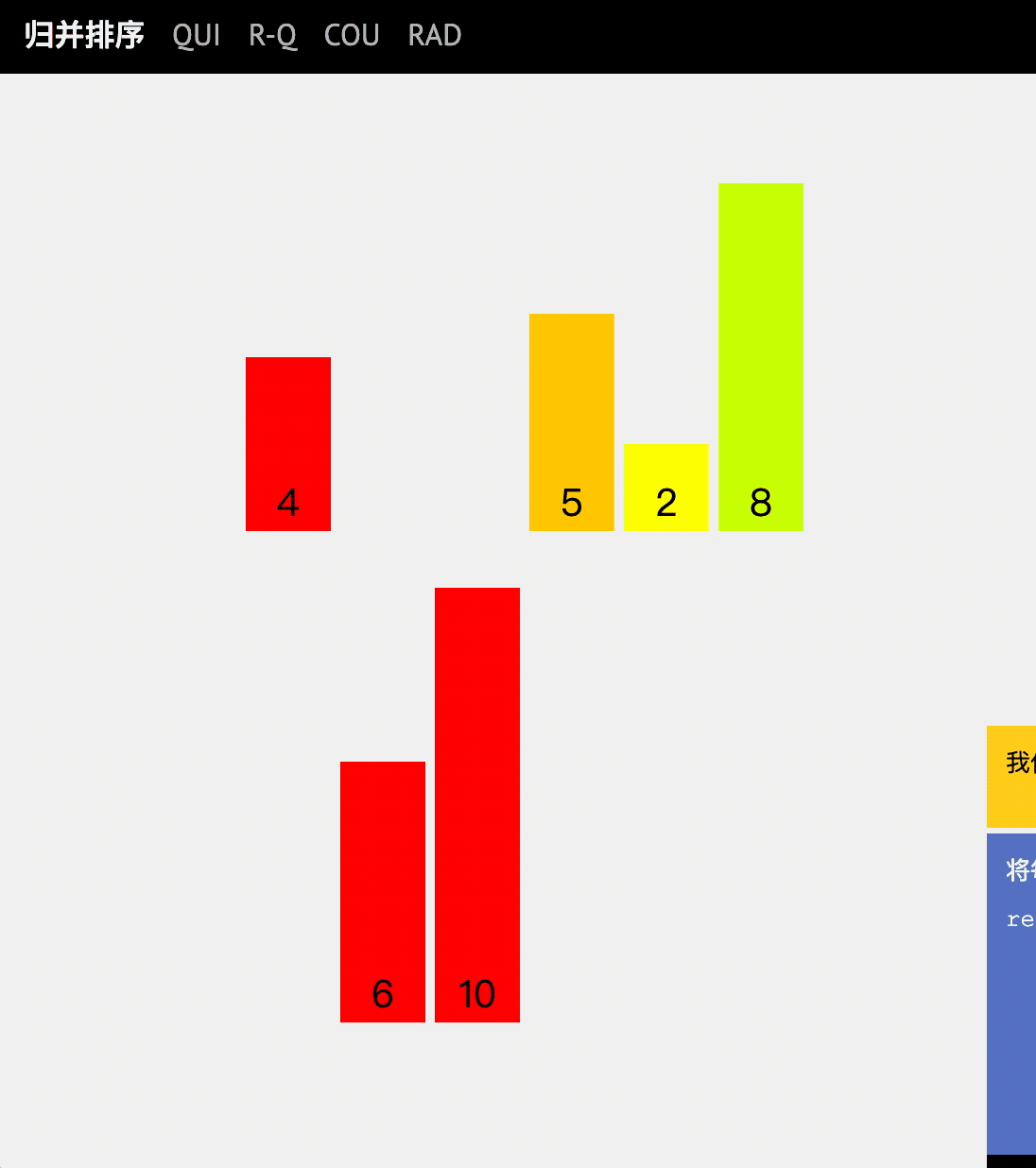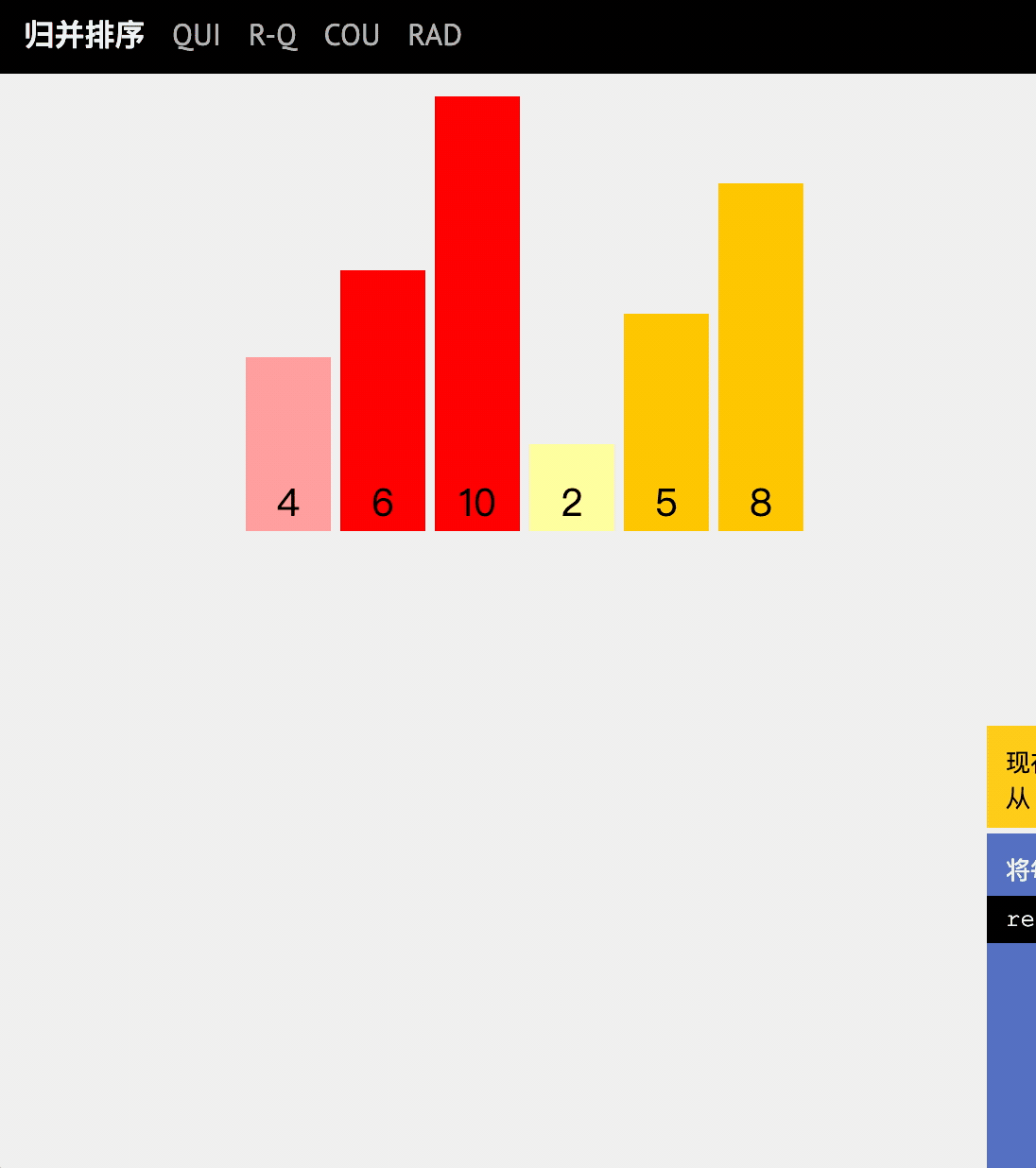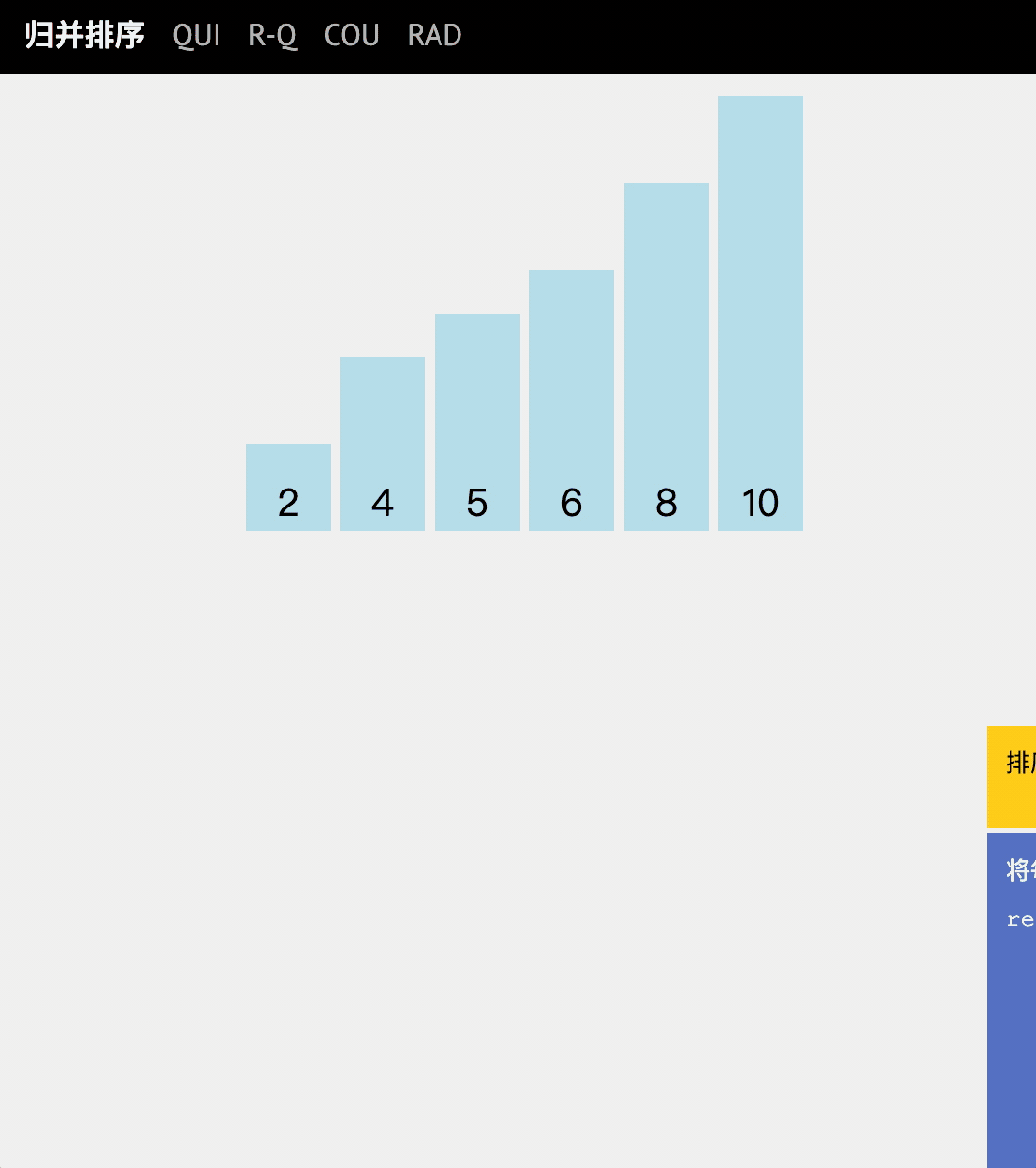
代码实现
public class MergeSort {
public static void sort(int[] array){
divide(array,0,array.length-1);
}
private static int[] divide(int[] array, int left, int right) {
int mid = (left+right)/2;
if(left<right){
divide(array,left,mid);
divide(array,mid+1,right);
//左右归并
merge(array,left,mid,right);
}
System.out.println(Arrays.toString(array));
return array;
}
public static void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[right-left+1];
int i= left;
int j = mid+1;
int k=0;
// 把较小的数先移到新数组中
while(i<=mid && j<=right){
if(array[i]<array[j]){
temp[k++] = array[i++];
}else{
temp[k++] = array[j++];
}
}
// 把左边剩余的数移入数组
while(i<=mid){
temp[k++] = array[i++];
}
// 把右边边剩余的数移入数组
while(j<=right){
temp[k++] = array[j++];
}
// 把新数组中的数覆盖nums数组
for(int x=0;x<temp.length;x++){
array[x+left] = temp[x];
}
}
}
输出结果
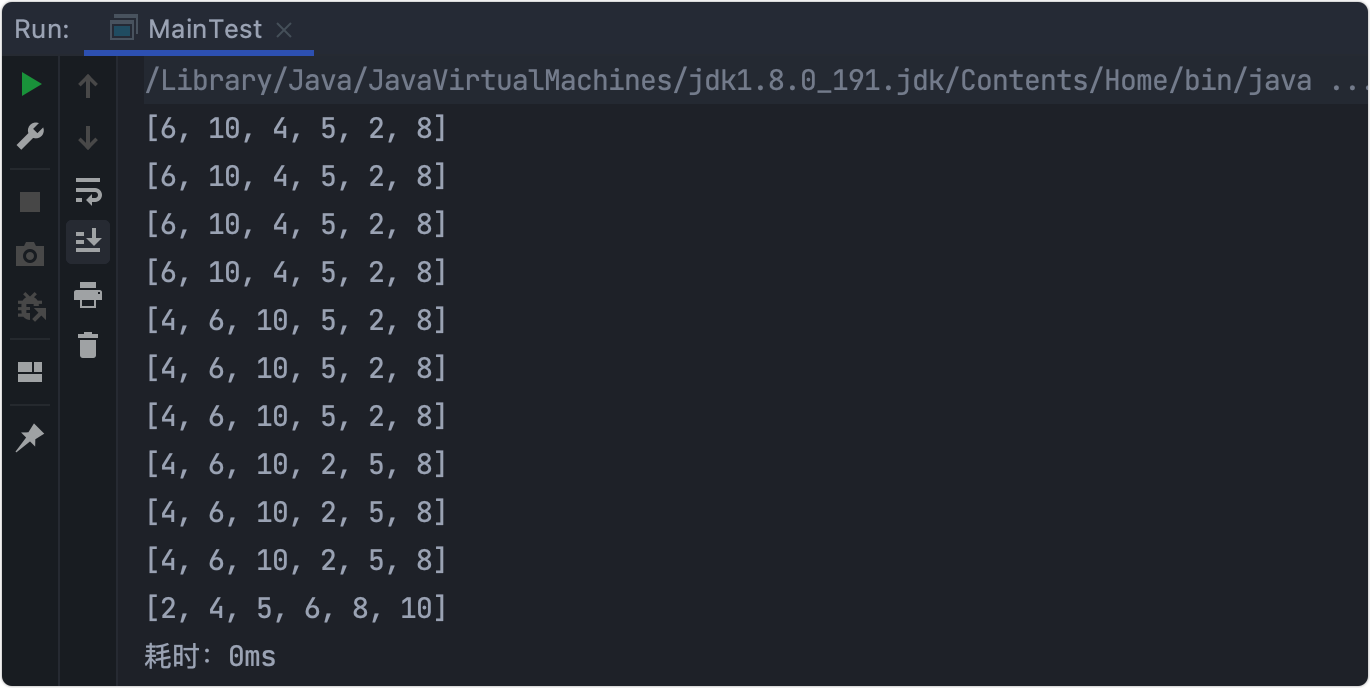
耗时测试

算法优化
计数排序
从这里开始都是非比较排序。
基本思想
假如输入一个数x,如果我们可以找到比该数小的数有几个,那么就可以直接将x放入到对应的输出数组的位置。
比如测试序列中的x=5,,比5小的有2个,那么毫无疑问5就该排在第三位。
动图讲解
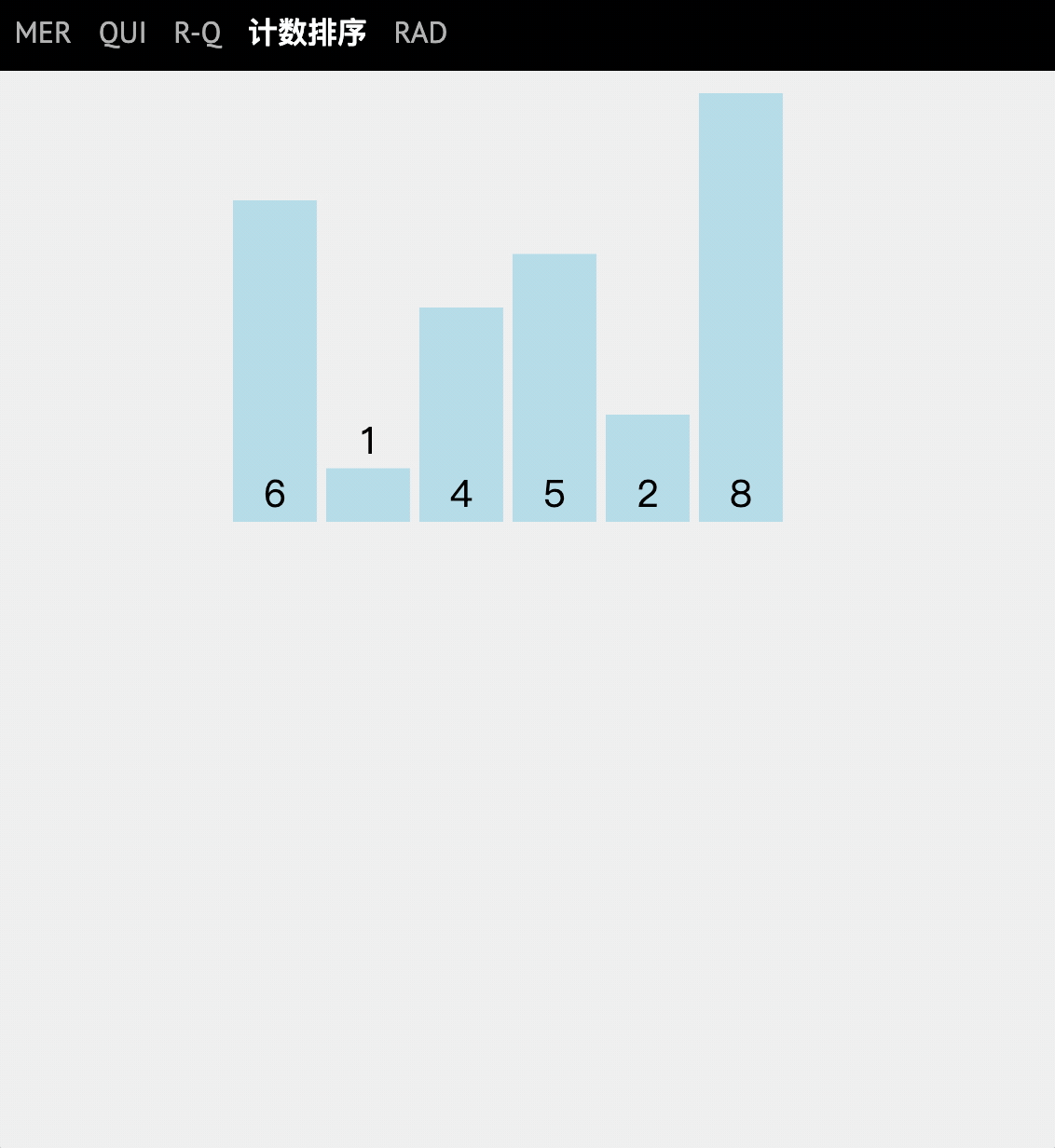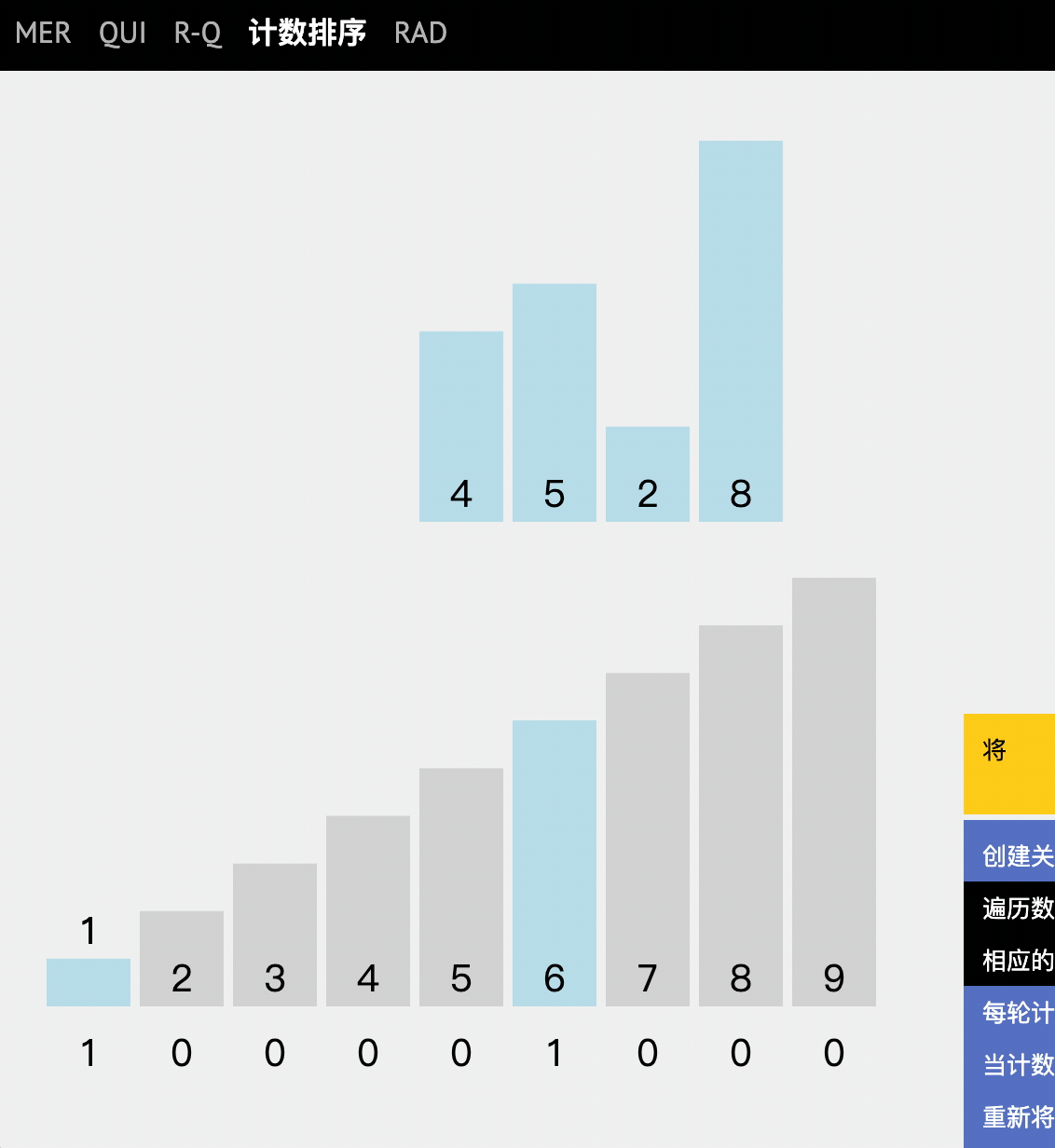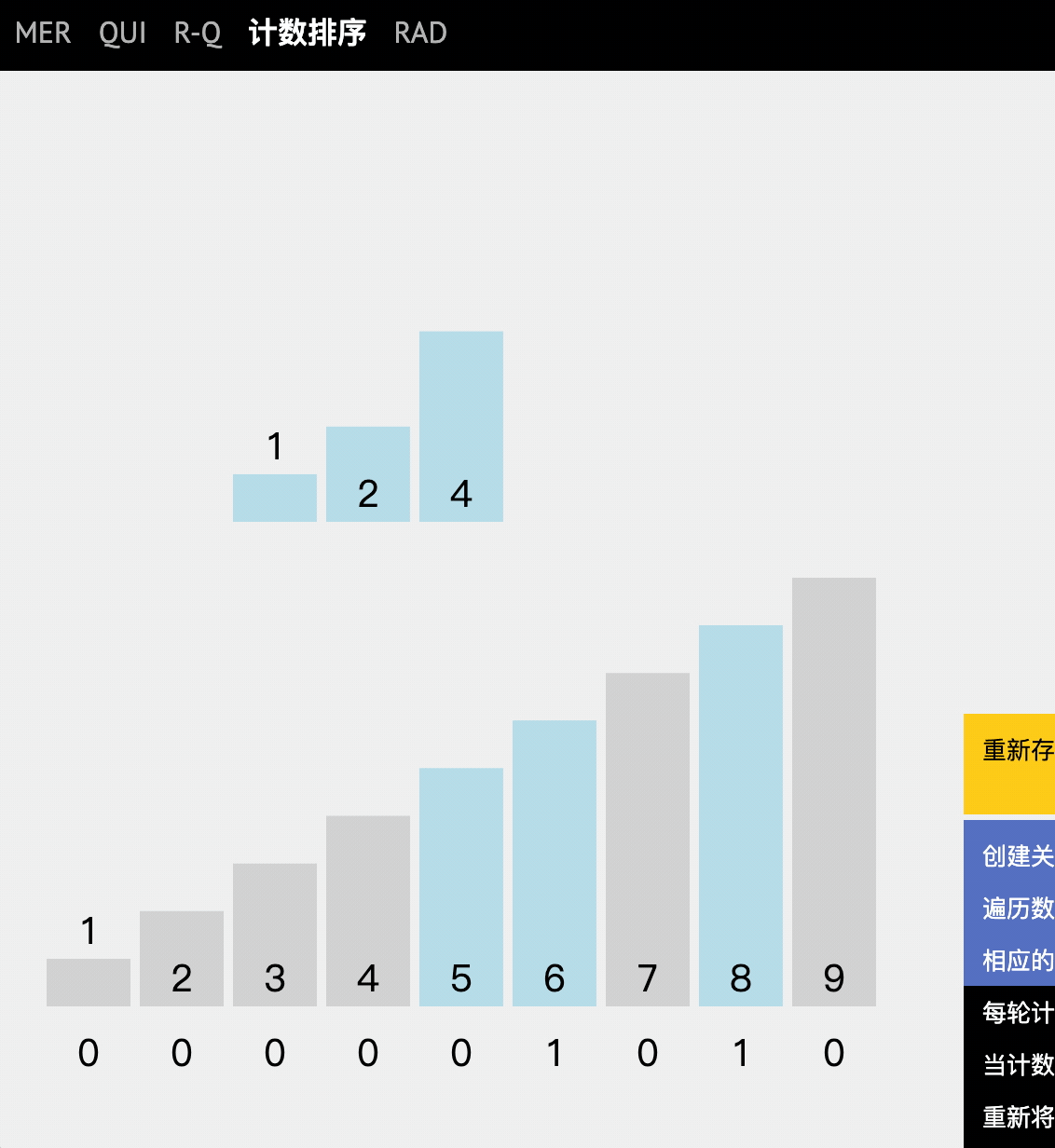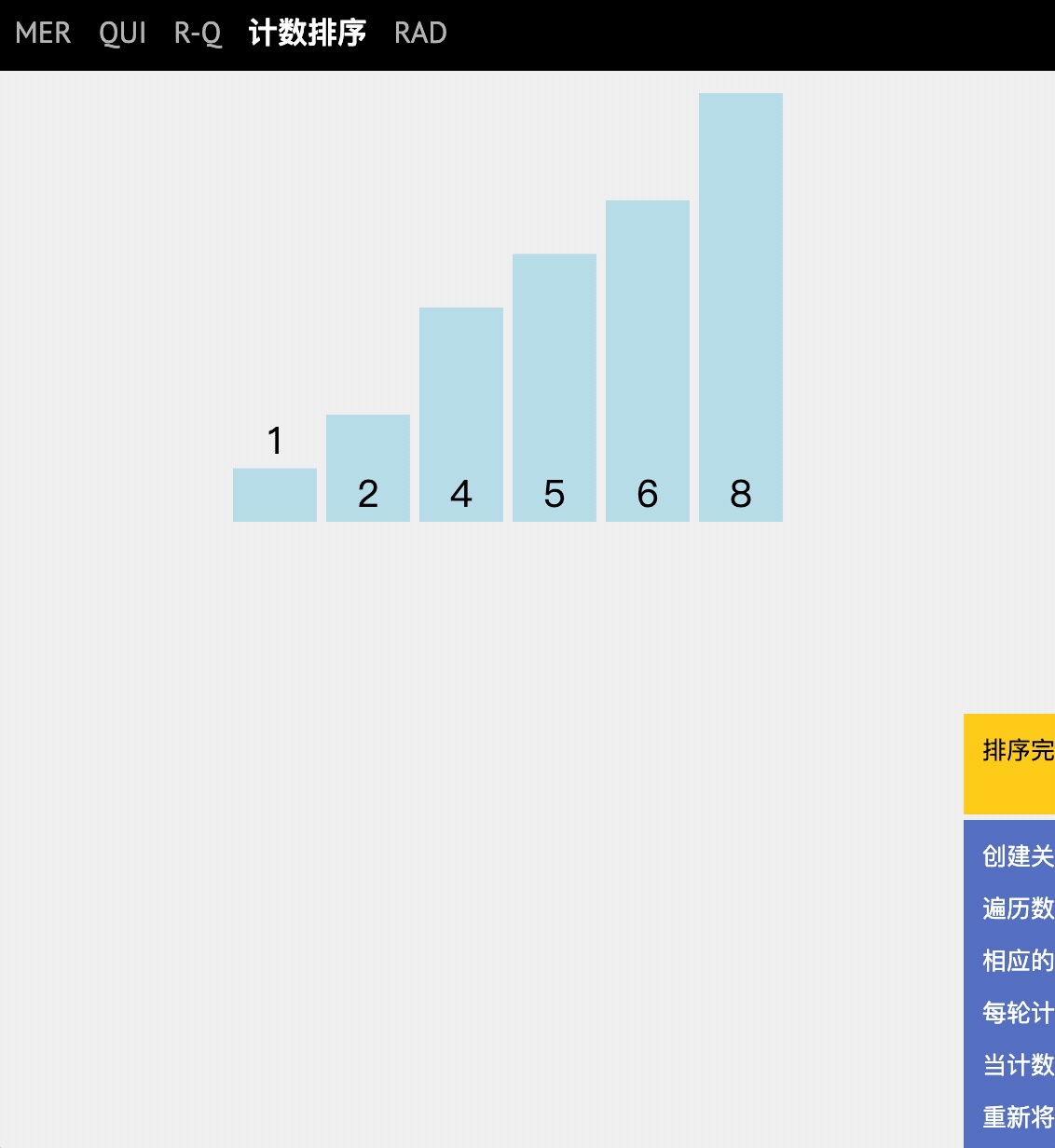
代码实现
public class CountSort {
public static void sort(int[] array) {
System.out.println("计数排序开始--------");
//计算最大值和最小值,用于确定count[]的长度
int max = array[0], min = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
//count[]用于存储每个元素出现的次数
int[] count = new int[max - min + 1];
//统计出现的频次
for (int i : array) {
count[i - min] += 1;//数的位置 上+1
}
//创建最终返回的数组,和原始数组长度相等,但是排序完成的
int[] result = new int[array.length];
int index = 0;//记录最终数组的下标
//先循环每一个元素 在计数排序器的下标中
for (int i = 0; i < count.length; i++) {
//遍历循环出现的次数
for (int j = 0; j < count[i]; j++) {//count[i]:这个数出现的频率
result[index++] = i + min;//以为原来减少了min现在加上min,值就变成了原来的值
}
System.out.println(Arrays.toString(result));
}
}
}
输出结果
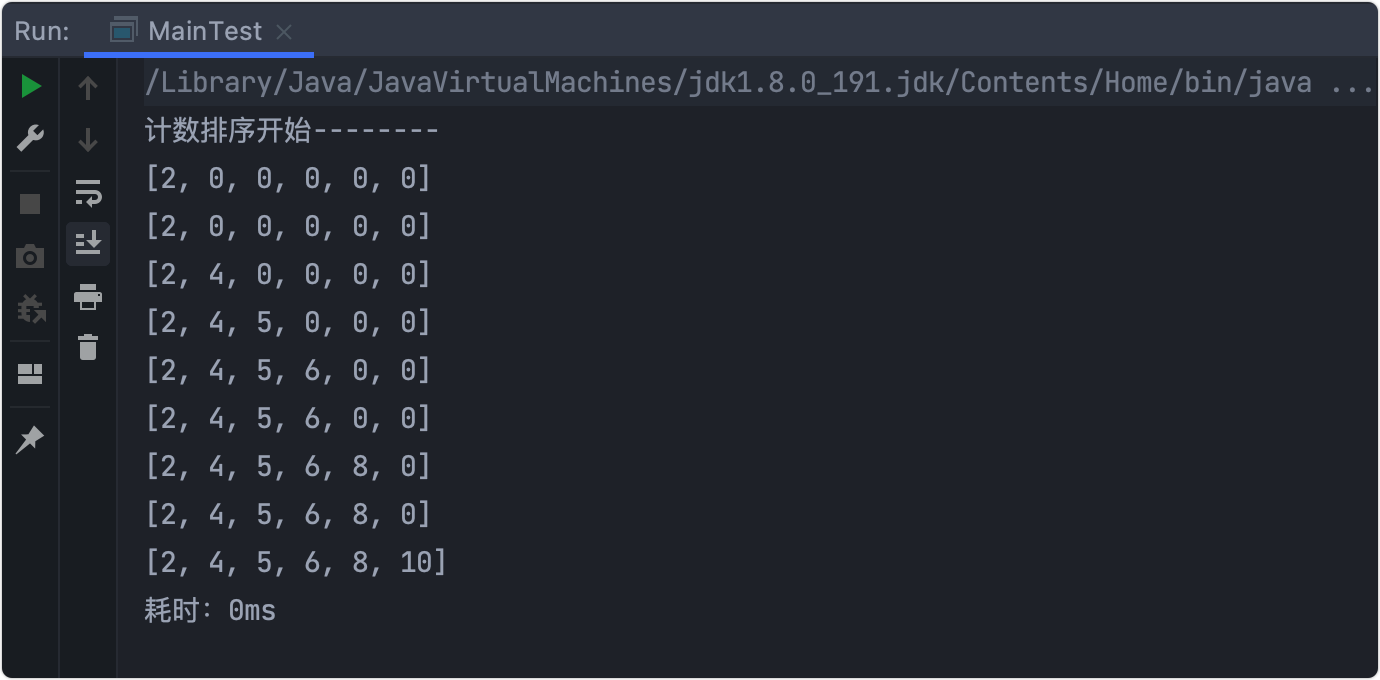
逐步分析
- 就是将原始数组中的数值出现的频率(次数)记录在新数组下标中。
- 遍历出现的次数,依次放入新数组。
耗时测试
说实话,这个速度都惊到我了。计数排序的时间复杂度是O(n),缺点是限制值域为[0,k]的整数。
算法优化
正常计数排序是从0开始的,本文实现的代码从min开始,已优化。
总结
本文并没有具体介绍时间复杂度,因为我放一个数字在这里你根本理解不了他们的差距。
用100000长度的数组测试八大排序算法,化抽象为具体。当数据量很大的时候 nlogn的优势将会比n^2越来越大,当n=10^5的时候,nlogn的算法要比n^2的算法快6000倍,什么概念呢,就是如果我们要处理一个数据集,用nlogn的算法要处理一天的话,用n^2的算法将要处理6020天。这就基本相当于是15年。
一个优化改进的算法可能比一个比一个笨的算法速度快了许多,这就是大厂考查算法和我们学习算法的原因。
古语云:乘众人之智,则无不任也;用众人之力,则无不胜也。为了攻克算法这座大山,我制定了组队刷题计划,每天至少1道leetcode算法题。
驽马十驾,功在不舍。
如果你刚刚大一,每天坚持学习,你将会至少比别人多刷1200道题,那么毕业时你的工资就可能是别人的3-4倍。
如果你是职场人,每天提升自己,升职加薪,成为技术专家指日可待。
只要你愿意去奋斗,始终走在拼搏的路上,那你的人生,最坏的结果,也不过是大器晚成。
点击文末卡片加入计划
粉丝专属福利
📚Java:1.5G学习资料——回复「资料」
📚算法:视频书籍——回复「算法」